Media heroniana
Contenido keyboard_arrow_down
En matemáticas, la Heronian mean H de dos números reales no negativos A y B es dado por la fórmula
Lleva el nombre de Herón de Alejandría.
Propiedades
Al igual que todas las medias, la media heroniana es simétrica (no depende del orden en que se dan sus dos argumentos) e idempotente (la media de cualquier número consigo mismo es el mismo número).
La media heroniana de los números A y B es un medio ponderado de sus medios aritméticos y geométricos: Por lo tanto, está entre estos dos medios, y entre los dos números dados.
Aplicación en geometría sólida
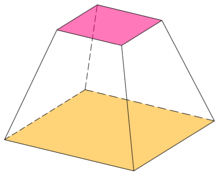
La media heroniana se puede utilizar para hallar el volumen de un tronco de pirámide o de un cono. El volumen es igual al producto de la altura del tronco y la media heroniana de las áreas de las caras paralelas opuestas.
Una versión de esta fórmula, para el cuadrado frusta, aparece en el Papiro Matemático de Moscú, del Antiguo Egipto, cuyo contenido data aproximadamente de 1850 a. C.
Referencias
- ^ a b c d Bullen, P.S. (2003), "2.1.4 Medios heronianos, centroidales y neo-patagóricos", Handbook of Means and Their Inequalities, Matemáticas y sus aplicaciones, Berlín, Nueva York: Springer Science+Business Media, pp. 399–401, doi:10.1007/978-94-017-0399-4, ISBN 978-1-4020-1522-9
- ^ Horatio N. Robinson (1860), "Teorema 22", Elementos de Geometría, Plane y Trigonometría Esférica, con Numerosos Problemas Prácticos, Nueva York: Ivisón, Phinney ' Co., págs. 210 a 211
- ^ Eves, Howard Whitley (1980), Great Moments in Mathematics (antes de 1650), Mathematical Association of America, pp. 11–13, ISBN 978-0-88385-310-8
Estadísticas | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Más resultados...