Media cuadrática

En matemáticas y sus aplicaciones, raíz media cuadrado de un conjunto de números ${displaystyle x_{i}}$ (abbreviado como RMS, RMS o rms y denotado en fórmulas como ${displaystyle x_{mathrm {RMS}}$ o ${displaystyle mathrm {RMS} _{x}$) se define como la raíz cuadrada de la plaza media (la media aritmética de los cuadrados) del conjunto. El RMS también es conocido como quadratic mean (denominado ${displaystyle M_{2}$) y es un caso particular de la media generalizada. El RMS de una función continuamente variable (denotado) ${displaystyle f_{mathrm {RMS}$) se puede definir en términos de una parte integral de los cuadrados de los valores instantáneos durante un ciclo.

Para la corriente eléctrica alterna, RMS es igual al valor de la corriente continua constante que produciría la misma disipación de potencia en una carga resistiva. En la teoría de la estimación, la desviación cuadrática media de un estimador es una medida de la imperfección del ajuste del estimador a los datos.

Definición

El valor RMS de un conjunto de valores (o una forma de onda de tiempo continuo) es la raíz cuadrada de la media aritmética de los cuadrados de los valores, o el cuadrado de la función que define la forma de onda continua. En física, el valor de corriente RMS también se puede definir como el "valor de la corriente continua que disipa la misma potencia en una resistencia."

En el caso de un conjunto de n valores ${displaystyle {x_{1},x_{2},dotsx_{n}}}$, el RMS es

${displaystyle x_{text{RMS}={sqrt {frac {1}{n}left} (x_{1}{2}+x_{2}{2}+cdots - Sí.$

La fórmula correspondiente para una función continua (o forma onda) f()t) definido en el intervalo ${displaystyle T_{1}leq tleq T_{2}$ es

${displaystyle F_{text{RMS}={{1 over {T_{2}-T_{1}}{int ¿Qué? {d}t}}}}$

y el RMS de una función durante todo el tiempo es

${displaystyle F_{text{RMS}=lim ################################################################################################################################################################################################################################################################ {d}t}}}}$

El RMS durante todo el tiempo de una función periódica es igual al RMS de un período de la función. El valor RMS de una función o señal continua se puede aproximar tomando el RMS de una muestra que consta de observaciones igualmente espaciadas. Además, el valor RMS de varias formas de onda también se puede determinar sin cálculo, como lo muestra Cartwright.

En el caso de la estadística RMS de un proceso aleatorio, se utiliza el valor esperado en lugar de la media.

En formas de onda comunes

Sine, cuadrado, triángulo y forma de onda de sierra. En cada uno, la línea central es a 0, el pico positivo está en ${displaystyle Y=A_{1}$ y el pico negativo está en ${displaystyle Y...$

Una onda de pulso rectangular del ciclo de trabajo D, la relación entre la duración del pulso (${displaystyle tau }$) y el período (T); ilustrado aquí con a = 1.

Gráfico del voltaje de una onda sine vs. el tiempo (en grados), mostrando RMS, pico (PK), y voltajes de pico a pico (PP).

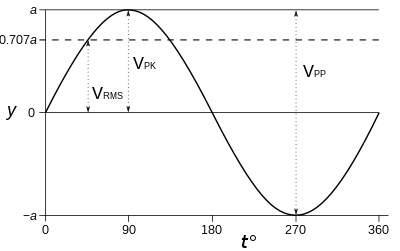
Si la forma de onda es una onda sinusoidal pura, las relaciones entre amplitudes (pico a pico, pico) y RMS son fijas y conocidas, como lo son para cualquier onda periódica continua. Sin embargo, esto no es cierto para una forma de onda arbitraria, que puede no ser periódica o continua. Para una onda sinusoidal de media cero, la relación entre RMS y la amplitud de pico a pico es:

Peak-to-peak ${displaystyle =2{sqrt {2}times {text{RMS}approx 2.8times {text{RMS}}$

Para otras formas de onda, las relaciones no son las mismas que para las ondas sinusoidales. Por ejemplo, para una onda triangular o de diente de sierra

Peak-to-peak ${displaystyle =2{sqrt {3}times {text{RMS}approx 3.5times {text{RMS}}$

Waveform	Variables y operadores	RMS
DC	${displaystyle y=A_{0},}$	${displaystyle A_{0},}$
Sine wave	${displaystyle y=A_{1}sin(2pi ft),}$	${displaystyle {frac {f}{sqrt {2}}} {f}}} {f}}} {f}} {f}}}}}}}} {f}}}} {f}}}}}}}}}} {f}}}$
Onda cuadrada	${displaystyle Y={begin{cases}A_{1} {frac} (ft) made0.5\-A_{1} {frac}(ft)}0.5end{cases}}$	${displaystyle A_{1},}$
DC-shifted Square wave	${displaystyle Y=A_{0}+{begin{cases}A_{1} limitoperatorname {frac} (ft) made0.5\-A_{1} limitoperatorname {frac} (ft)}0.5end{cases}$	${fnMicrosoft Sans {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif}$
Moda de seno modificada	${displaystyle y={begin{cases}0 ventajaoperatorname {frac} (ft) made0.25A_{1} limit0.25 Secutor {frac} (ft) seleccion0.5$ Contenido relacionado Aleksandr Lyapunov Teorema del punto fijo de Brouwer GH Hardy Más resultados... Te puede interesar Tamaño del texto: Pequeño Mediano Grande Copiar Editar Resumir undoredo format_boldformat_italicformat_underlinedstrikethrough_ssuperscriptsubscriptlink save cancelcheck_circle