Media

Hay varios tipos de medias en matemáticas, especialmente en estadística. Cada media sirve para resumir un grupo determinado de datos, a menudo para comprender mejor el valor general (magnitud y signo) de un conjunto de datos determinado.

Para un conjunto de datos, el aritmética media, también conocido como "medioaritmético", es una medida de tendencia central de un conjunto finito de números: específicamente, la suma de los valores divididos por el número de valores. La media aritmética de un conjunto de números x₁, x₂,..., x_n se denota típicamente usando una barra superior, x̄ ̄ {displaystyle {bar {x}}. Si los datos se basaron en una serie de observaciones obtenidas mediante muestreo de una población estadística, la media aritmética es la muestra media ()x̄ ̄ {displaystyle {bar {x}}) para distinguirlo de la media, o valor esperado, de la distribución subyacente, el población media (denominado μ μ {displaystyle mu } o μ μ x{displaystyle mu _{x}}).

Aparte de la probabilidad y la estadística, a menudo se utiliza una amplia gama de otras nociones de media en geometría y análisis matemático; a continuación se dan ejemplos.

Tipos de medios

Pitagórico significa

Media aritmética (AM)

La media aritmética (o simplemente #) de una lista de números, es la suma de todos los números divididos por el número de números. Del mismo modo, la media de una muestra x1,x2,...... ,xn{displaystyle x_{1},x_{2},ldotsx_{n}, generalmente denotado por x̄ ̄ {displaystyle {bar {x}}, es la suma de los valores muestreados divididos por el número de elementos en la muestra.

x̄ ̄ =1n().. i=1nxi)=x1+x2+⋯ ⋯ +xnn{displaystyle {bar {x}={frac {1}{n}left(sum)} ¿Por qué? {x_{1}+x_{2}+cdots - Sí.

Por ejemplo, la media aritmética de cinco valores: 4, 36, 45, 50, 75 es:

4+36+45+50+755=2105=42.{fnMicroc} {4+36+45+50+75}={frac {210}=42}

Media geométrica (GM)

La media geométrica es un promedio que sirve para conjuntos de números positivos, que se interpretan según su producto (como es el caso de las tasas de crecimiento) y no según su suma (como es el caso de la media aritmética):

x̄ ̄ =()∏ ∏ i=1nxi)1n=()x1x2⋯ ⋯ xn)1n{displaystyle {bar {x}=left(prod) ¿Qué? {1}{n}=left(x_{1}x_{2}cdots x_{n}right)^{frac {1}{n}}

Por ejemplo, la media geométrica de cinco valores: 4, 36, 45, 50, 75 es:

()4× × 36× × 45× × 50× × 75)15=243000005=30.{displaystyle (4times 36times 45times 50times 75)^{frac {1} {5}={5}}=30.}

Media armónica (HM)

La media armónica es un promedio que es útil para conjuntos de números que se definen en relación con alguna unidad, como en el caso de la velocidad (es decir, la distancia por unidad de tiempo):

x̄ ̄ =n().. i=1n1xi)− − 1{displaystyle {bar {x}=nleft(sum) - ¿Qué? {1}{x_{i}}derecha)} {-1}

Por ejemplo, la media armónica de los cinco valores: 4, 36, 45, 50, 75 es

514+136+145+150+175=513=15.{displaystyle {frac}{tfrac {1}{4}+{tfrac {1}{36}+{tfrac {1}{45}+{tfrac {1}{50}+{tfrac {1}{75}}={frac} {fnMicroc} {1}};}=15.}

Relación entre AM, GM y HM

Prueba sin palabras de la desigualdad de medios aritméticos y geométricos:
PR{displaystyle PR. es el diámetro de un círculo centrado en O{displaystyle O.; su radio AO{displaystyle AO! es la media aritmética de a{displaystyle a} y b{displaystyle b}. Usando el teorema geométrico medio, triángulo PGR{displaystyle PGR}'s altitud GQ{displaystyle GQ. es la media geométrica. Para cualquier relación a:b{displaystyle a:b}, AO≥ ≥ GQ{displaystyle AOgeq GQ}.

AM, GM y HM satisfacen estas desigualdades:

AM≥ ≥ GM≥ ≥ HM{displaystyle mathrm {AM} geq mathrm {GM} geq mathrm {HM} ,}

La igualdad se cumple si todos los elementos de la muestra dada son iguales.

Ubicación estadística

Comparación de la media aritmética, mediana y modo de dos distribuciones (log-normal).

Visualización geométrica del modo, mediana y media de una función de densidad de probabilidad arbitraria.

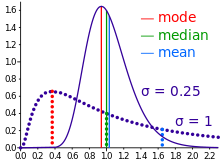
En las estadísticas descriptivas, la media puede confundirse con la mediana, la moda o el rango medio, ya que cualquiera de estos puede llamarse incorrectamente "promedio" (más formalmente, una medida de tendencia central). La media de un conjunto de observaciones es la media aritmética de los valores; sin embargo, para distribuciones sesgadas, la media no es necesariamente la misma que el valor medio (mediana) o el valor más probable (moda). Por ejemplo, la renta media suele estar sesgada hacia arriba por un pequeño número de personas con ingresos muy elevados, de modo que la mayoría tiene una renta inferior a la media. Por el contrario, la renta mediana es el nivel en el que la mitad de la población está por debajo y la otra mitad por encima. La modalidad renta es la renta más probable y favorece al mayor número de personas con rentas más bajas. Si bien la mediana y la moda suelen ser medidas más intuitivas para tales datos sesgados, muchas distribuciones sesgadas se describen mejor por su media, incluidas las distribuciones exponencial y de Poisson.

Media de una distribución de probabilidad

La media de una distribución de probabilidad es el valor promedio aritmético de largo plazo de una variable aleatoria que tiene esa distribución. Si la variable aleatoria es denotada por X{displaystyle X}, entonces también se conoce como el valor esperado de X{displaystyle X} (denominado E()X){displaystyle E(X)}). Para una distribución discreta de probabilidad, el medio es dado por .. xP()x){displaystyle textstyle sum xP(x)}, donde se toma la suma sobre todos los valores posibles de la variable aleatoria y P()x){displaystyle P(x)} es la función de masa de probabilidad. Para una distribución continua, la media es ∫ ∫ − − JUEGO JUEGO JUEGO JUEGO xf()x)dx{displaystyle textstyle int _{-infty }{infty }xf(x),dx}, donde f()x){displaystyle f(x)} es la función de densidad de probabilidad. En todos los casos, incluyendo aquellos en los que la distribución no es discreta ni continua, la media es la Lebesgue integral de la variable aleatoria con respecto a su medida de probabilidad. La necesidad media no existe o ser finita; para algunas distribuciones de probabilidad el medio es infinito (+ o JUEGO), mientras que para otros el medio es indefinido.

Medios generalizados

Potencia media

La media generalizada, también conocida como media de potencia o media de Hölder, es una abstracción de las medias cuadrática, aritmética, geométrica y armónica. Se define para un conjunto de n números positivos x_i por

x̄ ̄ ()m)=()1n.. i=1nxim)1m{displaystyle {bar {x}(m)=left({frac {1}{n}sum} ¿Por qué? {1}{m}}

Al elegir diferentes valores para el parámetro m, se obtienen los siguientes tipos de medias:

limm→ → JUEGO JUEGO {displaystyle lim _{mto infty}

máximo xi{displaystyle x_{i}}

limm→ → 2{displaystyle lim _{mto 2}

quadratic mean

limm→ → 1{displaystyle lim _{mto 1}

aritmética media

limm→ → 0{displaystyle lim _{mto 0}

geométrica

limm→ → − − 1{displaystyle lim _{mto -1}

armónico

limm→ → − − JUEGO JUEGO {displaystyle lim _{mto -infty }

mínimo xi{displaystyle x_{i}}

F-media

Esto se puede generalizar aún más como la media f generalizada

x̄ ̄ =f− − 1()1n.. i=1nf()xi)){displaystyle {bar {x}=f^{-1}left({{frac {1}{n}}sum} ¿Por qué?

y de nuevo una elección adecuada de un invertible f dará

f()x)=x{displaystyle f(x)=x}	aritmética significa,
f()x)=1x{displaystyle f(x)={frac {1}{x}}	significa armónico,
f()x)=xm{displaystyle f(x)=x^{m}	poder significa,
f()x)=In⁡ ⁡ ()x){displaystyle f(x)=ln(x)}	Medio geométrico.

Media aritmética ponderada

La media aritmética ponderada (o promedio ponderado) se usa si se desea combinar valores promedio de muestras de diferentes tamaños de la misma población:

x̄ ̄ =.. i=1nwixī ̄ .. i=1nwi.{displaystyle {bar {x}={frac {fnMicroc} ¿Qué? {fnK}} {fnK}} {fnK}}}}} {f}}}} {f}}} {f}}}}}} {f}}}}}}} {f}}}}} {f}}}}}}}} {f}}}}}}}}} {f}}}}}}}}}} { - Sí.

Donde xī ̄ {displaystyle {bar {x_{i}}}} y wi{displaystyle ¿Qué? son la media y el tamaño de la muestra i{displaystyle i} respectivamente. En otras aplicaciones, representan una medida para la fiabilidad de la influencia sobre el medio por los valores respectivos.

Media truncada

A veces, un conjunto de números puede contener valores atípicos (es decir, valores de datos que son mucho más bajos o más altos que los demás). A menudo, los valores atípicos son datos erróneos causados por artefactos. En este caso, se puede utilizar una media truncada. Implica descartar partes dadas de los datos en el extremo superior o inferior, generalmente una cantidad igual en cada extremo y luego tomar la media aritmética de los datos restantes. El número de valores eliminados se indica como un porcentaje del número total de valores.

Media intercuartil

La media intercuartil es un ejemplo específico de una media truncada. Es simplemente la media aritmética después de eliminar el cuarto de valores más bajo y más alto.

x̄ ̄ =2n.. i=n4+134nxi{displaystyle {bar {x}={frac} {2} {n};be} _{i={frac {fn}}+1} {fnK} {fn}}}}}}} {fn} {fn} {fn} {fn} {fn} {fn}}}} {fn}}}}}}}}}}}}}\\fn} {fn}}} {f}}}}}}}}}}}}}}}}}}}\\\\\\\f}}}}}}}}}}}}\\\\\\\\\f}}}}}}}}}}}}}}}}}}\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\ {3}n}n}!

suponiendo que los valores se hayan ordenado, es simplemente un ejemplo específico de una media ponderada para un conjunto específico de pesos.

Media de una función

En algunas circunstancias, los matemáticos pueden calcular una media de un conjunto infinito (o incluso incontable) de valores. Esto puede suceder al calcular el valor medio Sí.avg{displaystyle y_{text{avg}} de una función f()x){displaystyle f(x)}. Intuitivamente, un medio de una función se puede considerar como calcular el área bajo una sección de una curva, y luego dividir por la longitud de esa sección. Esto se puede hacer crudamente contando cuadrados en papel gráfico, o más precisamente por integración. La fórmula de integración está escrita como:

Sí.avg()a,b)=1b− − a∫ ∫ abf()x)dx{displaystyle y_{text{avg}(a,b)={frac {1}{b-a}int limits _{a}{b}f(x),dx}

En este caso, se debe tener cuidado para asegurarse de que la integral converja. Pero la media puede ser finita incluso si la función misma tiende a infinito en algunos puntos.

Media de ángulos y cantidades cíclicas

Los ángulos, las horas del día y otras cantidades cíclicas requieren aritmética modular para sumar y combinar números. En todas estas situaciones, no habrá un medio único. Por ejemplo, los tiempos de una hora antes y después de la medianoche son equidistantes tanto de la medianoche como del mediodía. También es posible que no exista un medio. Considere una rueda de colores: no hay media para el conjunto de todos los colores. En estas situaciones, debe decidir qué medio es más útil. Puede hacerlo ajustando los valores antes de promediar o utilizando un enfoque especializado para la media de cantidades circulares.

Medio Fréchet

La media de Fréchet da una manera de determinar el "centro" de una distribución de masa en una superficie o, más generalmente, variedad de Riemann. A diferencia de muchas otras medias, la media de Fréchet se define en un espacio cuyos elementos no necesariamente se pueden sumar o multiplicar por escalares. A veces también se conoce como la media de Karcher (llamada así por Hermann Karcher).

Regla de Swanson

Esta es una aproximación a la media de una distribución moderadamente sesgada. Se utiliza en la exploración de hidrocarburos y se define como:

m=0.3P10+0,4P50+0.3P90{displaystyle m=0.3P_{10}+0.4P_{50}+0.3P_{90}

donde P₁₀, P₅₀ y P₉₀ Percentiles 10, 50 y 90 de la distribución.

Otros medios