Mecanismo de tornillo

El tornillo es un mecanismo que convierte el movimiento rotatorio en movimiento lineal y un par (fuerza rotatoria) en una fuerza lineal. Es una de las seis máquinas simples clásicas. La forma más común consiste en un eje cilíndrico con ranuras o crestas helicoidales llamadas roscas alrededor del exterior. El tornillo pasa a través de un orificio en otro objeto o medio, con roscas en el interior del orificio que se engranan con las roscas del tornillo. Cuando el eje del tornillo gira en relación con las roscas estacionarias, el tornillo se mueve a lo largo de su eje en relación con el medio que lo rodea; por ejemplo, al girar un tornillo para madera se fuerza a entrar en la madera. En los mecanismos de tornillo, el eje del tornillo puede girar a través de un orificio roscado en un objeto estacionario, o un collar roscado como una tuerca puede girar alrededor de un eje de tornillo estacionario. Geométricamente, un tornillo puede verse como un plano inclinado estrecho que envuelve un cilindro.

Al igual que otras máquinas simples, un tornillo puede amplificar la fuerza; una pequeña fuerza rotacional (par) sobre el eje puede ejercer una gran fuerza axial sobre una carga. Cuanto menor sea el paso (la distancia entre las roscas del tornillo), mayor será la ventaja mecánica (la relación entre la fuerza de salida y la de entrada). Los tornillos se utilizan ampliamente en elementos de sujeción roscados para mantener unidos objetos y en dispositivos como tapas de rosca para contenedores, prensas de tornillo, gatos de tornillo y prensas de tornillo.

Otros mecanismos que utilizan el mismo principio, también llamados tornillos, no necesariamente tienen un eje o roscas. Por ejemplo, un sacacorchos es una varilla en forma de hélice con una punta afilada, y un tornillo de Arquímedes es una bomba de agua que utiliza una cámara helicoidal giratoria para mover el agua cuesta arriba. El principio común de todos los tornillos es que una hélice giratoria puede provocar un movimiento lineal.

El tornillo fue una de las últimas máquinas sencillas que se inventaron. Apareció por primera vez en Mesopotamia durante el período neoasirio (911-609) a. C. y luego apareció en el Antiguo Egipto y la Antigua Grecia.

Los registros indican que el tornillo de agua, o bomba de tornillo, se utilizó por primera vez en el Antiguo Egipto, algún tiempo antes de que el filósofo griego Arquímedes describiera la bomba de agua de tornillo de Arquímedes alrededor del año 234 a. C. Arquímedes escribió el primer estudio teórico del tornillo como máquina y se considera que introdujo el tornillo en la Antigua Grecia. En el siglo I a. C., el tornillo se utilizaba en forma de prensa de tornillo y tornillo de Arquímedes.

Los filósofos griegos definieron el tornillo como una de las máquinas simples y pudieron calcular su ventaja mecánica (ideal). Por ejemplo, Herón de Alejandría (52 d. C.) incluyó el tornillo como uno de los cinco mecanismos que podían "poner una carga en movimiento", lo definió como un plano inclinado que envolvía un cilindro y describió su fabricación y usos, incluso describió un macho para cortar roscas hembra.

Debido a que su complicada forma helicoidal debía cortarse laboriosamente a mano, los tornillos solo se usaban como elementos de unión en unas pocas máquinas en el mundo antiguo. Los tornillos de fijación solo comenzaron a usarse en el siglo XV en los relojes, después de que se desarrollaran los tornos de corte de tornillos. Al parecer, el tornillo también se aplicó para perforar y mover materiales (además del agua) en esa época, cuando comenzaron a aparecer imágenes de barrenas y taladros en las pinturas europeas. La teoría dinámica completa de las máquinas simples, incluido el tornillo, fue elaborada por el científico italiano Galileo Galilei en 1600 en Le Meccaniche ("Sobre la mecánica").

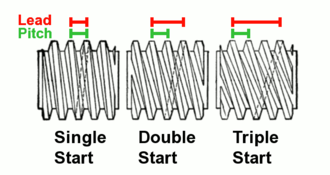
La finura o aspereza de las roscas de un tornillo se definen mediante dos magnitudes estrechamente relacionadas:

• El plomo se define como la distancia axial (paralela al eje del tornillo) el tornillo viaja en una revolución completa (360°) del eje. El plomo determina la ventaja mecánica del tornillo; cuanto menor sea el plomo, mayor será la ventaja mecánica.
• El lanzamiento se define como la distancia axial entre las crestas de los hilos adyacentes.

En la mayoría de los tornillos, llamados tornillos de "una sola entrada", que tienen una sola rosca helicoidal envuelta alrededor de ellos, el paso y el avance son iguales. Solo difieren en los tornillos de "varias entradas", que tienen varias roscas entrelazadas. En estos tornillos, el paso es igual al paso multiplicado por el número de "entradas". Los tornillos de varias entradas se utilizan cuando se desea un gran movimiento lineal para una rotación dada, por ejemplo, en tapas de rosca de botellas y bolígrafos.

La hélice de la rosca de un tornillo puede girar en dos direcciones posibles, lo que se conoce como lateralidad. La mayoría de las roscas de los tornillos están orientadas de manera que, cuando se las ve desde arriba, el eje del tornillo se aleja del observador (el tornillo se aprieta) cuando se gira en el sentido de las agujas del reloj. Esto se conoce como rosca diestra (RH), porque sigue la regla de agarre de la mano derecha: cuando los dedos de la mano derecha se curvan alrededor del eje en la dirección de rotación, el pulgar apuntará en la dirección del movimiento del eje. Las roscas orientadas en la dirección opuesta se conocen como zurdas (LH).

Por convención común, la mano derecha es la mano por defecto para las roscas de los tornillos. Por lo tanto, la mayoría de las piezas y elementos de fijación roscados tienen roscas derechas. Una explicación de por qué las roscas derechas se convirtieron en estándar es que para una persona diestra, apretar un tornillo diestro con un destornillador es más fácil que apretar un tornillo zurdo, porque utiliza el músculo supinador más fuerte del brazo en lugar del músculo pronador más débil. Dado que la mayoría de las personas son diestras, las roscas derechas se convirtieron en estándar en los elementos de fijación roscados.

Las conexiones de tornillo en las máquinas son una excepción; pueden ser dextrógiras o zurdas, según cuál sea más aplicable. Las roscas de tornillo zurdas también se utilizan en otras aplicaciones:

• Donde la rotación de un eje causaría que una tuerca convencional de la derecha se afloje en lugar de apretar debido a la precesión inducida por fresamiento. Por ejemplo:
  • El pedal izquierdo en bicicleta.
  • El tornillo izquierdo que sostiene una hoja de sierra circular o una rueda de rectificadora de banco.
• En algunos dispositivos que tienen hilos en ambos extremos, como volquetes y segmentos de tuberías extraíbles. Estas partes tienen un hilo de mano derecha y de mano izquierda, de modo que girar la pieza endurece o afloja ambos hilos al mismo tiempo.
• En algunas conexiones de suministro de gas para prevenir conexiones peligrosas. Por ejemplo, en la soldadura de gas la línea de suministro de gas inflamable se adjunta con hilos de mano izquierda, por lo que no se cambiará accidentalmente con el suministro de oxígeno, que utiliza hilos de mano derecha.
• Para hacerlos inútiles para el público (por lo que desalienta el robo), se utilizan bombillas de mano izquierda en algunas estaciones de tren y metro.
• Se dice que las tapas de ataúd se han mantenido tradicionalmente con tornillos zurdos.

En los tornillos que se emplean para distintos fines se utilizan distintas formas (perfiles) de roscas. Las roscas de los tornillos están estandarizadas para que las piezas fabricadas por distintos fabricantes encajen correctamente.

El ángulo de rosca es el ángulo comprendido, medido en una sección paralela al eje, entre las dos caras de apoyo de la rosca. El ángulo entre la fuerza de carga axial y la normal a la superficie de apoyo es aproximadamente igual a la mitad del ángulo de rosca, por lo que el ángulo de rosca tiene un gran efecto en la fricción y la eficiencia de un tornillo, así como en la tasa de desgaste y la resistencia. Cuanto mayor sea el ángulo de rosca, mayor será el ángulo entre el vector de carga y la normal a la superficie, por lo que mayor será la fuerza normal entre las roscas necesaria para soportar una carga dada. Por lo tanto, al aumentar el ángulo de rosca, aumenta la fricción y el desgaste de un tornillo.

La superficie de apoyo de la rosca en ángulo orientada hacia afuera, cuando se ve afectada por la fuerza de carga, también aplica una fuerza radial (hacia afuera) a la tuerca, lo que provoca tensión de tracción. Esta fuerza de ruptura radial aumenta con el aumento del ángulo de la rosca. Si la resistencia a la tracción del material de la tuerca es insuficiente, una carga excesiva sobre una tuerca con un ángulo de rosca grande puede partirla.

El ángulo de la rosca también influye en la resistencia de la misma; las roscas con un ángulo grande tienen una raíz más ancha en comparación con su tamaño y son más resistentes.

En los elementos de fijación roscados, se aceptan y suelen desear grandes cantidades de fricción para evitar que el elemento de fijación se desenrosque. Por eso, las roscas que se utilizan en los elementos de fijación suelen tener un ángulo de rosca grande de 60°:

• a) Hilo V - Estos se utilizan en tornillos autotapping tales como tornillos de madera y tornillos de chapa de metal que requieren un borde afilado para cortar un agujero, y donde se necesita fricción adicional para asegurarse de que el tornillo permanece inmóvil, como en tornillos y tornillos de ajuste, y donde la articulación debe ser fluido ajustado como en las articulaciones de tubo roscado.
• b) American National - Esto ha sido reemplazado por la norma unificada casi idéntica. Tiene el mismo ángulo de hilo de 60° que el hilo V pero es más fuerte debido a la raíz plana. Se utiliza en pernos, nueces y una amplia variedad de sujetadores.
• c) Hilos métricos - Estos hilos se especifican y son comunes para los estándares ISO y DIN.
• d) Whitworth o British Standard - Estándar británico muy similar reemplazado por la norma Unified Thread.

En cambio, en los mecanismos de unión de máquinas, como husillos de avance o de elevación, es necesario minimizar la fricción, por lo que se utilizan roscas con ángulos más pequeños:

• e) Hilo cuadrado - Este es el hilo de fricción más fuerte y más bajo, con un ángulo de rosca de 0°, y no aplica fuerza expansiva a la tuerca. Sin embargo, es difícil fabricar, requiriendo una herramienta de corte de un solo punto debido a la necesidad de cortar los bordes. Se utiliza en aplicaciones de alta carga como tornillos y tornillos de plomo, pero ha sido reemplazado principalmente por el hilo Acme. A hilo cuadrado modificado con un pequeño ángulo de hilo de 5° se utiliza a veces, que es más barato para la fabricación.
• f) Hilos de acme - Con su ángulo de hilo de 28° tiene una fricción más alta que el hilo cuadrado, pero es más fácil de fabricar y se puede utilizar con una nuez dividida para ajustarse para el desgaste. Es ampliamente utilizado en vises, C-clamps, válvulas, tijeras y tornillos de plomo en máquinas como tornos.
• g) Hilo de mantequilla - Esto se utiliza en aplicaciones de alta carga en las que la fuerza de carga se aplica sólo en una dirección, como tornillos. Con un ángulo de 0° de la superficie de rodamiento es tan eficiente como el hilo cuadrado pero más fuerte y fácil de fabricar.
• h) Hilo de nudillo - Similar a un hilo cuadrado en el que se han redondeado las esquinas para protegerlas del daño, dándole también una fricción superior. En aplicaciones de baja resistencia se puede fabricar barato de la hoja de material mediante laminado. Se utiliza en bombillas y enchufes.

• Debido a su propiedad autobloqueante (ver abajo) el tornillo es ampliamente utilizado en sujetadores roscados para mantener los objetos o materiales juntos: el tornillo de madera, el tornillo de chapa, el clavo y el tornillo y la tuerca.
• La propiedad de autobloqueo también es clave para el uso del tornillo en una amplia gama de otras aplicaciones, como el corkscrew, la tapa del contenedor superior de tornillo, la articulación de tuberías roscadas, vise, C-clamp y el tornillo.
• Los tornillos también se utilizan como enlaces en máquinas para transferir energía, en el equipo de gusano, tornillo de plomo, tornillo de bola y tornillo de rodillo. Debido a su baja eficiencia, los vínculos de tornillo rara vez se utilizan para llevar una alta potencia, pero se emplean más a menudo en usos de baja potencia, intermitentes como los actuadores de posicionamiento.
• Las cuchillas de tornillo de helicoidal giratorio o las cámaras se utilizan para mover material en el tornillo de Arquímedes, taladro de tierra de aullido y transportador de tornillo.
• El micrometro utiliza un tornillo calibrado de precisión para longitudes de medición con gran precisión.

La hélice, aunque comparte el nombre de tornillo, funciona según principios físicos muy diferentes a los de los tipos de hélice mencionados anteriormente, y la información de este artículo no se aplica a ella.

La distancia lineal ${\displaystyle d\,}$ un eje de tornillo se mueve cuando se gira a través de un ángulo ${\displaystyle \alpha \,}$ grados es:

${\displaystyle d=l{\fnMicroc}{360^{\circ ♪♪$

Donde ${\displaystyle l\,}$ es la pista del tornillo.

La razón de distancia de una máquina simple se define como la razón entre la distancia que recorre la fuerza aplicada y la distancia que recorre la carga. En el caso de un tornillo, es la razón entre la distancia circular d_in que recorre un punto del borde del eje y la distancia lineal d_out que recorre el eje. Si r es el radio del eje, en una vuelta un punto del borde del tornillo recorre una distancia de 2πr, mientras que su eje se mueve linealmente la distancia de avance l. Por lo tanto, la razón de distancia es

${\displaystyle {\mbox{distance ratio}\equiv {\frac} {\fn} {\fn} {\fnK}} {\fn}} {\fnK}} {\fn}}} {\fn}}} {\fn}} {\fnK}}}}} {\fn\fn}}}} {\fn\f}}}}}} {\fnK\f}}}}}} {\f}} {\f}}}}}}}}} {\f}}}}}}}}}}}} {\f} {\f}}}}}}}}}}}}}}}}}}}}}}}} {\f} {\f} {\f} {\f}} {\f} {\f}\fn\f}\fn\f} {\f}}}}}}\fn\f}\f}\f}\fn\fn\fn\fn\fn\f}}\fn\fn\fn\fn\f}}}\fn {2\pi} {\fnMicrosoft Sans Serif}$

La ventaja mecánica MA de un tornillo se define como la relación entre la fuerza axial de salida F_out aplicada por el eje sobre una carga y la fuerza de rotación F_in aplicada al borde del eje para girarlo. Para un tornillo sin fricción (también llamado tornillo ideal), a partir de la conservación de la energía, el trabajo realizado sobre el tornillo por la fuerza de entrada que lo hace girar es igual al trabajo realizado por el tornillo sobre la fuerza de carga:

${\displaystyle ¿Qué?$

El trabajo es igual a la fuerza multiplicada por la distancia que actúa, por lo que el trabajo realizado en un giro completo del tornillo es ${\displaystyle W_{in}=2\pi .$ y el trabajo hecho en la carga es ${\displaystyle ¿Qué?$. Así que... ideal ventaja mecánica de un tornillo es igual a la relación entre la distancia:

Se puede ver que la ventaja mecánica de un tornillo depende de su ventaja, ${\displaystyle l\,}$. Cuanto menor sea la distancia entre sus hilos, mayor será la ventaja mecánica, y mayor será la fuerza que el tornillo puede ejercer para una fuerza aplicada dada. Sin embargo la mayoría de los tornillos reales tienen grandes cantidades de fricción y su ventaja mecánica es menos que dada por la ecuación anterior.

La fuerza de rotación aplicada al tornillo es en realidad un par ${\displaystyle T_{in}=F_{in}r\,}$. Debido a esto, la fuerza de entrada necesaria para girar un tornillo depende de cuán lejos del eje se aplica; más lejos del eje, se necesita menos fuerza para girarlo. La fuerza en un tornillo no se aplica generalmente en el borde como se asumió anteriormente. A menudo se aplica por alguna forma de palanca; por ejemplo, un perno es girado por una llave cuyo mango funciona como una palanca. La ventaja mecánica en este caso se puede calcular utilizando la longitud del brazo de palanca para r en la ecuación anterior. Este factor extraneoso r se puede quitar de la ecuación anterior escribiendo en términos de par:

${\displaystyle {\frac {\fnh} {\fn}}={\fn} {\fnh}} {\fn}} {\fn}} {\fn}}}}} {\fnK}}}} {\fn}}} {\fnK}}}}}} {\fnK\f}}}}} {\f}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}} {\f} {\f}\f}}}}}}}}}}}}}}}}}}}}\f}}}}}}}}\f}}}}}}}}} {\ {2\pi}{l}\,}$

Debido a la gran área de contacto deslizante entre las roscas móviles y estacionarias, los tornillos suelen tener grandes pérdidas de energía por fricción. Incluso los tornillos de nivelación bien lubricados tienen eficiencias de solo el 15% - 20%, el resto del trabajo aplicado al girarlos se pierde por fricción. Cuando se incluye la fricción, la ventaja mecánica ya no es igual a la relación de distancia, sino que también depende de la eficiencia del tornillo. A partir de la conservación de la energía, el trabajo W_in realizado en el tornillo por la fuerza de entrada al girarlo es igual a la suma del trabajo realizado al mover la carga W_out y el trabajo disipado como calor por la fricción W_fric en el tornillo

${\displaystyle ¿Qué?$

La eficiencia η es un número adimensional entre 0 y 1 definido como la relación entre el trabajo de salida y el trabajo de entrada

${\displaystyle \eta ¿Qué?$

${\displaystyle W_{out}=\eta ¿Qué?$

El trabajo se define como la fuerza multiplicada por la distancia movida, así ${\displaystyle ¿Qué?$ y ${\displaystyle ¿Qué?$ por lo tanto

${\displaystyle F_{out}d_{out}=\eta F_{in}d_{in}\,}$

${\displaystyle {\frac {\f} {\fn}}=\eta} {\fnMicroc {d_{in} {d_{out}}\,}$

o en términos de par motor

${\displaystyle {\frac {\fnh} {\fn}}={\fn} {\fnh}} {\fn}} {\fn}} {\fn}}}}} {\fnK}}}} {\fn}}} {\fnK}}}}}} {\fnK\f}}}}} {\f}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}} {\f} {\f}\f}}}}}}}}}}}}}}}}}}}}\f}}}}}}}}\f}}}}}}}}} {\ {2\pi \eta }\qquad \,}$

Así que la ventaja mecánica de un tornillo real se reduce de lo que sería en un tornillo ideal, sin fricción por la eficiencia ${\displaystyle \eta \,}$. Debido a su baja eficiencia, en los tornillos de maquinaria alimentada no se utilizan a menudo como vínculos para transferir grandes cantidades de energía, pero se utilizan más a menudo en los posicionadores que operan intermitentemente.

Las grandes fuerzas de fricción hacen que la mayoría de los tornillos en uso práctico sean "autoblocantes", también llamados "no recíprocos" o "sin revisión". Esto significa que aplicar un par al eje hará que gire, pero ninguna cantidad de fuerza de carga axial contra el eje hará que gire en sentido contrario, incluso si el par aplicado es cero. Esto contrasta con algunas otras máquinas simples que son "recíprocas" o "sin bloqueo", lo que significa que si la fuerza de carga es lo suficientemente grande se moverán hacia atrás o se "revisarán". Por lo tanto, la máquina se puede utilizar en cualquier dirección. Por ejemplo, en una palanca, si la fuerza en el extremo de carga es demasiado grande, se moverá hacia atrás, realizando trabajo sobre la fuerza aplicada. La mayoría de los tornillos están diseñados para ser autoblocantes y, en ausencia de torque en el eje, permanecerán en la posición en la que se los deje. Sin embargo, algunos mecanismos de tornillo con un paso lo suficientemente grande y una buena lubricación no son autoblocantes y se revisarán, y muy pocos, como un taladro de empuje, usan el tornillo en este sentido "hacia atrás", aplicando fuerza axial al eje para girar el tornillo. Otras razones por las que los tornillos se aflojan son el diseño incorrecto del conjunto y las fuerzas externas, como golpes, vibraciones y cargas dinámicas que causan deslizamiento en las superficies roscadas y acopladas/sujetadas.

Esta propiedad de autobloqueo es una de las razones del uso tan extendido del tornillo en elementos de fijación roscados, como tornillos para madera, tornillos para chapa metálica, pernos y tacos. Al apretar el elemento de fijación girándolo se aplica una fuerza de compresión sobre los materiales o las piezas que se están fijando, pero ninguna cantidad de fuerza ejercida por las piezas hará que el tornillo gire hacia atrás y se afloje. Esta propiedad también es la base para el uso de tornillos en tapas de contenedores con tapa de rosca, prensas, abrazaderas en C y gatos de tornillo. Se puede levantar un objeto pesado girando el eje del gato, pero cuando se suelta el eje, permanecerá a la altura a la que se eleve.

Un tornillo será autobloqueante si y sólo si su eficiencia ${\displaystyle \eta \,}$ es inferior al 50%.

${\displaystyle \eta ={\frac {\fn} {\fn} {\fn}} {\fn}}= {\fn}} {\fn}} {\fn}} {\fn}}} {\fn}}} {\fn}}} {\fn}} {\f}}} {\f}}}}} {\fn} {\f} {\f}}}}}} {\f} {\f}} {\f}}}} {\f} {\f} {\f}}}}}} {\f}}}} {\f} {\f} {\f} {\f}}}}}}}}}} {\f}} {\f}}} {\f} {\f} {\f}} {\f} {\f}}}}}}}} {\f} {\f} {\f} {\f}}}} {\f}}}}\f}}}}}\f}}}}}}}}}}}}}}}}} {\fn} {\f} {\fn} {\fnK} {\f} {\f}} {\f} {\f}} {\f}} {\fn}} {\f}}} {\fn}}} {\fn}} {\f}} {\f}} {\f}}}} {\f}}}}}} {\f}}}} {\f}}}}}} {\f}} {\f}}}} {\f}}}} {\f}}}} {\f}}}} {\f} {\f} {\f}}} {\f}}}}}}}}}} {\f}}}}} {\f} {\f}}}} {\f}}} {\f}}}}} {\f}} {\f} {\f} {\f}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

El hecho de que un tornillo sea autoblocante depende en última instancia del ángulo de paso y del coeficiente de fricción de las roscas; las roscas muy bien lubricadas, de baja fricción y con un paso lo suficientemente grande pueden "repararse". También se deben tener en cuenta consideraciones para garantizar que los componentes sujetos estén sujetos con la suficiente firmeza para evitar el movimiento por completo. De lo contrario, pueden producirse deslizamientos en las roscas o en la superficie de sujeción.