Mecánica de fluidos
La mecánica de fluidos es la rama de la física que se ocupa de la mecánica de los fluidos (líquidos, gases y plasmas) y las fuerzas que actúan sobre ellos. Tiene aplicaciones en una amplia gama de disciplinas, incluida la ingeniería mecánica, aeroespacial, civil, química y biomédica, así como geofísica, oceanografía, meteorología, astrofísica y biología.
Se puede dividir en estática de fluidos, el estudio de los fluidos en reposo; y dinámica de fluidos, el estudio del efecto de las fuerzas sobre el movimiento de los fluidos. Es una rama de la mecánica del continuo, una materia que modela la materia sin utilizar la información de que está formada por átomos; es decir, modela la materia desde un punto de vista macroscópico en lugar de uno microscópico.
La mecánica de fluidos, especialmente la dinámica de fluidos, es un campo de investigación activo, típicamente matemáticamente complejo. Muchos problemas están parcial o totalmente sin resolver y la mejor manera de abordarlos es mediante métodos numéricos, normalmente utilizando computadoras. Una disciplina moderna, llamada dinámica de fluidos computacional (CFD), está dedicada a este enfoque. La velocimetría de imágenes de partículas, un método experimental para visualizar y analizar el flujo de fluidos, también aprovecha la naturaleza altamente visual del flujo de fluidos.
Historia
El estudio de la mecánica de fluidos se remonta al menos a los días de la antigua Grecia, cuando Arquímedes investigó la estática y la flotabilidad de los fluidos y formuló su famosa ley conocida ahora como la Ley de Arquímedes. principio, que fue publicado en su trabajo Sobre cuerpos flotantes, generalmente considerado como el primer trabajo importante sobre mecánica de fluidos. El erudito iraní Abu Rayhan Biruni y más tarde Al-Khazini aplicaron métodos científicos experimentales a la mecánica de fluidos. El rápido avance en la mecánica de fluidos comenzó con Leonardo da Vinci (observaciones y experimentos), Evangelista Torricelli (inventó el barómetro), Isaac Newton (investigó la viscosidad) y Blaise Pascal (investigó la hidrostática, formuló la ley de Pascal), y fue continuado por Daniel Bernoulli con la introducción de la dinámica de fluidos matemática en Hydrodynamica (1739).
Varios matemáticos (Jean le Rond d'Alembert, Joseph Louis Lagrange, Pierre-Simon Laplace, Siméon Denis Poisson) analizaron más a fondo el flujo no viscoso y una multitud de ingenieros, entre ellos Jean Léonard Marie Poiseuille y Siméon Denis Poisson, exploraron el flujo viscoso. Gotthilf Hagen. Claude-Louis Navier y George Gabriel Stokes proporcionaron una justificación matemática adicional en las ecuaciones de Navier-Stokes, y se investigaron las capas límite (Ludwig Prandtl, Theodore von Kármán), mientras que varios científicos como Osborne Reynolds, Andrey Kolmogorov y Geoffrey Ingram Taylor avanzó en la comprensión de la viscosidad y la turbulencia de los fluidos.
Sucursales principales
Estática de fluidos
La estática de fluidos o hidrostática es la rama de la mecánica de fluidos que estudia los fluidos en reposo. Abarca el estudio de las condiciones bajo las cuales los fluidos están en reposo en equilibrio estable; y se contrasta con la dinámica de fluidos, el estudio de los fluidos en movimiento. La hidrostática ofrece explicaciones físicas para muchos fenómenos de la vida cotidiana, como por qué la presión atmosférica cambia con la altitud, por qué la madera y el aceite flotan en el agua y por qué la superficie del agua siempre está nivelada cualquiera que sea la forma de su recipiente. La hidrostática es fundamental para la hidráulica, la ingeniería de equipos para almacenar, transportar y utilizar fluidos. También es relevante para algunos aspectos de la geofísica y la astrofísica (por ejemplo, para comprender la tectónica de placas y las anomalías en el campo gravitacional de la Tierra), la meteorología, la medicina (en el contexto de la presión arterial) y muchos otros campos. .
Dinámica de fluidos
La dinámica de fluidos es una subdisciplina de la mecánica de fluidos que se ocupa del flujo de fluidos: la ciencia de los líquidos y gases en movimiento. La dinámica de fluidos ofrece una estructura sistemática, que subyace a estas disciplinas prácticas, que abarca leyes empíricas y semiempíricas derivadas de la medición del flujo y utilizadas para resolver problemas prácticos. La solución a un problema de dinámica de fluidos normalmente implica calcular varias propiedades del fluido, como velocidad, presión, densidad y temperatura, como funciones del espacio y el tiempo. Tiene varias subdisciplinas, incluida la aerodinámica (el estudio del aire y otros gases en movimiento) y la hidrodinámica (el estudio de líquidos en movimiento). La dinámica de fluidos tiene una amplia gama de aplicaciones, incluido el cálculo de fuerzas y movimientos en aviones, la determinación del caudal másico de petróleo a través de oleoductos, la predicción de patrones climáticos en evolución, la comprensión de las nebulosas en el espacio interestelar y el modelado de explosiones. Algunos principios de dinámica de fluidos se utilizan en ingeniería de tráfico y dinámica de multitudes.
Relación con la mecánica del continuo
La mecánica de fluidos es una subdisciplina de la mecánica continua, como se ilustra en la siguiente tabla.
| mecánicos continuos El estudio de la física de materiales continuos | Metal mecánica El estudio de la física de materiales continuos con una forma de reposo definida. | Elasticidad Describe materiales que regresan a su forma de reposo después de las tensiones aplicadas se eliminan. | |
| Plástico Describe materiales que deforman permanentemente después de un estrés aplicado suficiente. | Rheology Estudio de materiales con características sólidas y fluidas. | ||
| mecánicos fluidos El estudio de la física de materiales continuos que deforman cuando son sometidos a una fuerza. | Fluido no newtoniano No se sometan a tasas de tensión proporcionales a la tensión de cocción aplicada. | ||
| Los líquidos newtonianos experimentan tasas de tensión proporcionales al estrés del tinte aplicado. | |||
Desde el punto de vista mecánico, un fluido es una sustancia que no soporta esfuerzos cortantes; por eso un fluido en reposo tiene la forma del vaso que lo contiene. Un fluido en reposo no tiene esfuerzo cortante.
Suposiciones
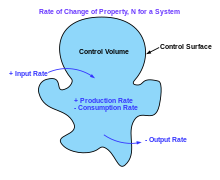
Las suposiciones inherentes a un tratamiento mecánico fluido de un sistema físico se pueden expresar en términos de ecuaciones matemáticas. Fundamentalmente, se asume que todo sistema mecánico fluido obedece:
- Conservación de las masas
- Conservación de la energía
- Conservación del impulso
- Suposición continua
Por ejemplo, la suposición de que la masa se conserva significa que para cualquier volumen de control fijo (por ejemplo, un volumen esférico) —cerrado por una superficie de control— la tasa de cambio de la masa contenida en ese volumen es igual a la tasa a la que la masa pasa por la superficie. afuera a dentro, menos la tasa a la que la masa está pasando dentro a afuera. Esto se puede expresar como una ecuación en forma integral sobre el volumen de control.
El suposición continua es una idealización de la mecánica continua bajo la cual los fluidos pueden ser tratados como continuos, aunque, a escala microscópica, están compuestos de moléculas. Bajo la suposición continuum, las propiedades macroscópicas (observadas/measurables) tales como densidad, presión, temperatura y velocidad de vracs se toman para ser bien definidas a los elementos de volumen "infinitesimales" —pequeñas en comparación con la escala de longitud característica del sistema, pero grandes en comparación con la escala de longitud molecular. Las propiedades fluidas pueden variar continuamente de un elemento de volumen a otro y son valores promedio de las propiedades moleculares. La hipótesis continua puede dar lugar a resultados inexactos en aplicaciones como flujos de velocidad supersónicos o flujos moleculares a escala nano. Los problemas para los que falla la hipótesis continua pueden resolverse utilizando la mecánica estadística. Para determinar si se aplica o no la hipótesis continuum, se evalúa el número de Knudsen, definido como la relación de la vía libre media molecular con la escala de longitud característica. Los problemas con los números de Knudsen inferiores a 0.1 se pueden evaluar utilizando la hipótesis continua, pero el enfoque molecular (mecanica estadística) se puede aplicar para encontrar el movimiento de fluido para los números Knudsen más grandes.
Ecuaciones de Navier-Stokes
El Ecuaciones Navier-Stokes (nombrado después de Claude-Louis Navier y George Gabriel Stokes) son ecuaciones diferenciales que describen el equilibrio de la fuerza en un punto dado dentro de un fluido. Para un fluido incompresible con campo de velocidad vectorial u{displaystyle mathbf {u}, las ecuaciones Navier-Stokes son
- ∂ ∂ u∂ ∂ t+()u⋅ ⋅ Silencio Silencio )u=− − 1*** *** Silencio Silencio p+. . Silencio Silencio 2u{displaystyle {frac {partial mathbf {u}{partial t}+(mathbf {u} cdot nabla)mathbf {u} =-{frac {1}{rho }nabla p+nu nabla ^{2}mathbf {u}.
Estas ecuaciones diferenciales son los análogos para materiales deformables a las ecuaciones de movimiento de Newton para partículas – las ecuaciones de Navier–Stokes describen cambios en el impulso (fuerza) en respuesta a la presión p{displaystyle p} y viscosidad, parametizada por la viscosidad cinemática . . {displaystyle nu }. Ocasionalmente, las fuerzas del cuerpo, como la fuerza gravitacional o la fuerza Lorentz se añaden a las ecuaciones.
Las soluciones de las ecuaciones de Navier-Stokes para un problema físico determinado deben buscarse con la ayuda del cálculo. En la práctica, sólo los casos más simples pueden resolverse exactamente de esta manera. Estos casos generalmente implican un flujo estable y no turbulento en el que el número de Reynolds es pequeño. Para casos más complejos, especialmente aquellos que involucran turbulencia, como sistemas climáticos globales, aerodinámica, hidrodinámica y muchos más, las soluciones de las ecuaciones de Navier-Stokes actualmente solo se pueden encontrar con la ayuda de computadoras. Esta rama de la ciencia se llama dinámica de fluidos computacional.
Fluidos invisidos y viscosos
An líquido invisivo no tiene viscosidad, . . =0{displaystyle nu =0}. En la práctica, un flujo invisivo es una idealización, que facilita el tratamiento matemático. De hecho, sólo se sabe que las corrientes puramente invisivas se realizan en el caso de la superfluididad. De lo contrario, los líquidos son generalmente viscous, una propiedad que es a menudo más importante dentro de una capa de límite cerca de una superficie sólida, donde el flujo debe coincidir en la condición de no-deslizante en el sólido. En algunos casos, las matemáticas de un sistema mecánico fluido pueden ser tratadas asumiendo que el fluido fuera de las capas de límites es invisivo, y luego coincide con su solución en eso para una capa de límite laminar delgada.
Para el flujo de fluido sobre un límite poroso, la velocidad del fluido puede ser discontinua entre el fluido libre y el fluido en el medio poroso (esto está relacionado con la condición de Beavers y Joseph). Además, a velocidades subsónicas bajas es útil suponer que el gas es incompresible, es decir, que la densidad del gas no cambia aunque cambien la velocidad y la presión estática.
Fluidos newtonianos versus no newtonianos
Un fluido newtoniano (llamado así en honor a Isaac Newton) se define como un fluido cuyo esfuerzo cortante es linealmente proporcional al gradiente de velocidad en la dirección perpendicular al plano de corte. Esta definición significa que independientemente de las fuerzas que actúan sobre un fluido, éste continúa fluyendo. Por ejemplo, el agua es un fluido newtoniano porque continúa mostrando propiedades fluidas sin importar cuánto se agite o mezcle. Una definición ligeramente menos rigurosa es que la resistencia de un objeto pequeño que se mueve lentamente a través del fluido es proporcional a la fuerza aplicada al objeto. (Compare la fricción). Los fluidos importantes, como el agua y la mayoría de los gases, se comportan (con buena aproximación) como un fluido newtoniano en condiciones normales en la Tierra.
Por el contrario, agitar un fluido no newtoniano puede dejar un "agujero" detrás. Este se llenará gradualmente con el tiempo; este comportamiento se observa en materiales como el pudín, el oobleck o la arena (aunque la arena no es estrictamente un fluido). Alternativamente, agitar un fluido no newtoniano puede hacer que la viscosidad disminuya, por lo que el fluido parece "más diluido" al mismo tiempo. (esto se ve en pinturas que no gotean). Hay muchos tipos de fluidos no newtonianos, ya que se definen como algo que no obedece a una propiedad particular; por ejemplo, la mayoría de los fluidos con largas cadenas moleculares pueden reaccionar de una manera no newtoniana.
Ecuaciones para un fluido newtoniano
La constante de proporcionalidad entre el tensor de tensión viscoso y el gradiente de velocidad se conoce como viscosidad. Una ecuación simple para describir el comportamiento de un fluido newtoniano incompresible es
- τ τ =− − μ μ dudn{displaystyle tau =-mu {mh00} ¿Qué? .
dónde
- τ τ {displaystyle tau } es el estrés del tinte ejercido por el fluido ("drag"),
- μ μ {displaystyle mu } es la viscosidad del fluido, una constante de proporcionalidad, y
- dudn{displaystyle {frac {mathrm} {mathrm}{mathrm {d} . es la velocidad gradiente perpendicular a la dirección del tinte.
Para un fluido Newtoniano, la viscosidad, por definición, depende sólo de la temperatura, no de las fuerzas que actúan sobre él. Si el fluido es incompresible la ecuación que rige el estrés viscoso (en coordenadas cartesianas) es
- τ τ ij=μ μ ()∂ ∂ vi∂ ∂ xj+∂ ∂ vj∂ ∂ xi){displaystyle tau _{ij}=muleft({frac {partial {fnK} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {f}}}} {fn}}} {fnMicrosoft}}}}} {f}}} {\fnMicrosoft}}}}}}}}}}} {\\\b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {fnK}} {fnMicroc {fnMicrosoft {fnMicrosoft} {f} {f}}} {fnMicroc} {\fnMicrosoft}}} {f}} {fn}}} {\fnMicroc {\fnMicroc}}}}}}}}}}}}\\\\\\\\\\\\\\\\\fnMicroc\\\\fn\\\\\\fn\\\\\\\\\\fn}\\fnMicroc}}\\\\\\\\\\\\\\\\\\\\\\\\\fn}\\\ ¿Qué?
dónde
- τ τ ij{displaystyle tau _{ij} es el estiércol de estrés ith{displaystyle i^{th}} cara de un elemento líquido en el jth{displaystyle j^{th} dirección
- vi{displaystyle V_{i} es la velocidad en la ith{displaystyle i^{th}} dirección
- xj{displaystyle x_{j} es jth{displaystyle j^{th} dirección coordenadas.
Si el líquido no es incompresible la forma general para el estrés viscoso en un líquido newtoniano es
- τ τ ij=μ μ ()∂ ∂ vi∂ ∂ xj+∂ ∂ vj∂ ∂ xi− − 23δ δ ijSilencio Silencio ⋅ ⋅ v)+κ κ δ δ ijSilencio Silencio ⋅ ⋅ v{displaystyle tau _{ij}=muleft({frac {partial {fnK} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {f}}}} {fn}}} {fnMicrosoft}}}}} {f}}} {\fnMicrosoft}}}}}}}}}}} {\\\b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {fnK} {fnMicroc {cHFF} {f}}{f}} {f}} {\fn}} {fnMicroc {fnMicrosoft {fn}}}} {\fn}}}}}}}}}\\\fnMicroc {\fn\\f}}}}}}}}}}}\\\\\\\\\\\fnfn\\\fnMicrocfn\\\\\\\\\fn\\\\fn}\\fnMicroc}}\\\\\\\fn}\\fn}\\\fn}fn\\\\\\\\\\fn ¿Por qué? {2}{3}delta _{ij}nabla cdot mathbf {v} right)+kappa delta _{ij}nabla cdot mathbf {v}
Donde κ κ {displaystyle kappa } es el segundo coeficiente de viscosidad (o viscosidad a granel). Si un líquido no obedece esta relación, se denomina un líquido no newtoniano, de los cuales hay varios tipos. Los fluidos no newtonianos pueden ser plásticos, plásticos Bingham, pseudoplásicos, dilatantes, thixotropic, reopectic, viscoelastic.
En algunas aplicaciones se realiza otra división áspera entre fluidos: fluidos ideales y no ideales. Un líquido ideal no es viscoso y no ofrece ninguna resistencia a una fuerza de arrastre. Un líquido ideal realmente no existe, pero en algunos cálculos, la suposición es justificable. Un ejemplo de esto es el flujo lejos de superficies sólidas. En muchos casos, los efectos viscosos se concentran cerca de los límites sólidos (como en las capas fronterizas) mientras que en las regiones del campo de flujo lejos de los límites se pueden descuidar los efectos viscosos y el líquido allí se trata como era invisivo (flujo ideal). Cuando se descuida la viscosidad, el término que contiene el tensor de estrés viscoso τ τ {displaystyle mathbf {tau } en la ecuación Navier-Stokes desaparece. La ecuación reducida en esta forma se llama la ecuación Euler.

















