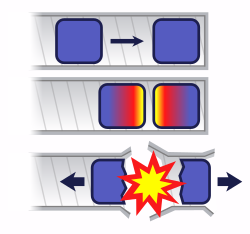
Masa critica

En ingeniería nuclear, una masa crítica es la cantidad más pequeña de material fisionable necesaria para una reacción nuclear en cadena sostenida. La masa crítica de un material fisionable depende de sus propiedades nucleares (específicamente, su sección transversal de fisión nuclear), densidad, forma, enriquecimiento, pureza, temperatura y entorno. El concepto es importante en el diseño de armas nucleares.
Explicación de la criticidad
Cuando una reacción nuclear en cadena en una masa de material fisible es autosuficiente, se dice que la masa se encuentra en un estado crítico en el que no hay aumento ni disminución de potencia, temperatura o población de neutrones.
Una medida numérica de una masa crítica depende del factor de multiplicación de neutrones efectivo k, el número promedio de neutrones liberados por evento de fisión que van para causar otro evento de fisión en lugar de ser absorbido o dejar el material. Cuando k = 1, la masa es crítica y la reacción en cadena es autosuficiente.
Una masa subcrítica es una masa de material fisible que no tiene la capacidad de sostener una reacción de fisión en cadena. Una población de neutrones introducida en un conjunto subcrítico disminuirá exponencialmente. En este caso, k < 1. Una tasa constante de fisiones espontáneas provoca un nivel proporcionalmente constante de actividad de neutrones. La constante de proporcionalidad aumenta a medida que aumenta k.
Una masa supercrítica es aquella que, una vez iniciada la fisión, procederá a un ritmo creciente. El material puede establecerse en equilibrio (es decir, volverse crítico de nuevo) a un nivel elevado de temperatura/potencia o destruirse a sí mismo. En el caso de supercriticidad, k > 1.
Debido a la fisión espontánea, una masa supercrítica sufrirá una reacción en cadena. Por ejemplo, una masa crítica esférica de uranio-235 puro (235U) con una masa de aproximadamente 52 kilogramos (115 lb) experimentaría alrededor de 15 eventos de fisión espontánea por segundo. La probabilidad de que uno de esos eventos cause una reacción en cadena depende de cuánto supere la masa a la masa crítica. Si hay uranio-238 (238U) presente, la tasa de fisión espontánea será mucho mayor. La fisión también puede ser iniciada por neutrones producidos por rayos cósmicos.
Cambiando el punto de criticidad
La masa donde ocurre la criticidad se puede cambiar modificando ciertos atributos como el combustible, la forma, la temperatura, la densidad y la instalación de una sustancia reflectante de neutrones. Estos atributos tienen interacciones e interdependencias complejas. Estos ejemplos solo describen los casos ideales más simples:
Variar la cantidad de combustible
Es posible que un conjunto de combustible sea crítico con una potencia casi nula. Si se añadiera la cantidad perfecta de combustible a una masa ligeramente subcrítica para crear una 'masa exactamente crítica', la fisión sería autosuficiente durante solo una generación de neutrones (el consumo de combustible hace que el conjunto vuelva a ser subcrítico).
Del mismo modo, si se añadiera la cantidad perfecta de combustible a una masa ligeramente subcrítica, para crear una masa apenas supercrítica, la temperatura del conjunto aumentaría hasta un máximo inicial (por ejemplo: 1 K por encima de la temperatura ambiente) y luego disminuir de nuevo a la temperatura ambiente después de un período de tiempo, porque el combustible consumido durante la fisión hace que el conjunto vuelva a la subcriticidad una vez más.
Cambiar la forma
Una masa puede ser exactamente crítica sin ser una esfera perfectamente homogénea. Refinar más de cerca la forma hacia una esfera perfecta hará que la masa sea supercrítica. Por el contrario, cambiar la forma a una esfera menos perfecta disminuirá su reactividad y la hará subcrítica.
Cambiar la temperatura
Una masa puede ser exactamente crítica a una temperatura particular. Las secciones transversales de fisión y absorción aumentan a medida que disminuye la velocidad relativa de los neutrones. A medida que aumenta la temperatura del combustible, los neutrones de una energía dada aparecen más rápido y, por lo tanto, la fisión/absorción es menos probable. Esto no es ajeno a la ampliación Doppler de las resonancias 238U, pero es común a todos los combustibles/absorbedores/configuraciones. Despreciando las resonancias muy importantes, la sección transversal total de neutrones de cada material exhibe una relación inversa con la velocidad relativa de los neutrones. El combustible caliente siempre es menos reactivo que el combustible frío (la moderación excesiva o insuficiente en LWR es un tema diferente). La expansión térmica asociada con el aumento de temperatura también contribuye con un coeficiente de reactividad negativo ya que los átomos de combustible se están separando más. Una masa que es exactamente crítica a temperatura ambiente sería subcrítica en un entorno por encima de la temperatura ambiente debido únicamente a la expansión térmica.
Variando la densidad de la masa
Cuanto mayor sea la densidad, menor será la masa crítica. La densidad de un material a una temperatura constante se puede cambiar variando la presión o la tensión o cambiando la estructura cristalina (ver alótropos de plutonio). Una masa ideal se volverá subcrítica si se le permite expandirse o, por el contrario, la misma masa se volverá supercrítica si se comprime. Cambiar la temperatura también puede cambiar la densidad; sin embargo, el efecto sobre la masa crítica se complica por los efectos de la temperatura (consulte "Cambio de la temperatura") y por si el material se expande o se contrae con el aumento de la temperatura. Suponiendo que el material se expande con la temperatura (por ejemplo, uranio-235 enriquecido a temperatura ambiente), en un estado exactamente crítico, se volverá subcrítico si se calienta a una densidad más baja o se volverá supercrítico si se enfría a una densidad más alta. Se dice que tal material tiene un coeficiente de reactividad de temperatura negativo para indicar que su reactividad disminuye cuando su temperatura aumenta. El uso de dicho material como combustible significa que la fisión disminuye a medida que aumenta la temperatura del combustible.
Uso de un reflector de neutrones
Rodear una masa crítica esférica con un reflector de neutrones reduce aún más la masa necesaria para la criticidad. Un material común para un reflector de neutrones es el metal berilio. Esto reduce la cantidad de neutrones que escapan del material fisionable, lo que aumenta la reactividad.
Uso de un tamper
En una bomba, una capa densa de material que rodea el núcleo fisible contendrá, por inercia, el material de fisión en expansión, lo que aumenta la eficiencia. Esto se conoce como manipulación. Un tamper también tiende a actuar como un reflector de neutrones. Debido a que una bomba se basa en neutrones rápidos (no moderados por la reflexión con elementos ligeros, como en un reactor), los neutrones reflejados por una manipulación se ralentizan por sus colisiones con los núcleos de la manipulación, y porque los neutrones reflejados tardan en regresar. al núcleo fisionable, tardan bastante más en ser absorbidos por un núcleo fisionable. Pero sí contribuyen a la reacción y pueden reducir la masa crítica en un factor de cuatro. Además, si el tamper es (por ejemplo, empobrecido) uranio, puede fisionarse debido a los neutrones de alta energía generados por la explosión primaria. Esto puede aumentar en gran medida el rendimiento, especialmente si se generan aún más neutrones al fusionar isótopos de hidrógeno, en una configuración denominada reforzada.
Tamaño crítico
El tamaño crítico es el tamaño mínimo del núcleo de un reactor nuclear o de un arma nuclear que se puede fabricar para una disposición geométrica y una composición de materiales específicas. El tamaño crítico debe incluir al menos suficiente material fisionable para alcanzar la masa crítica. Si el tamaño del núcleo del reactor es inferior a un cierto mínimo, se escapan demasiados neutrones de fisión a través de su superficie y la reacción en cadena no se mantiene.
Masa crítica de una esfera desnuda
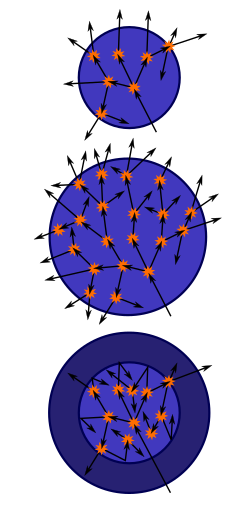
Medio: Al aumentar la masa de la esfera a una masa crítica, la reacción puede llegar a ser autosuficiente.
Tema: Alrededor de la esfera original con un reflector de neutrones aumenta la eficiencia de las reacciones y también permite que la reacción se vuelva autosuficiente.
La forma con masa crítica mínima y las dimensiones físicas más pequeñas es una esfera. Las masas críticas de esfera desnuda a densidad normal de algunos actínidos se enumeran en la siguiente tabla. La mayor parte de la información sobre masas de esferas desnudas se considera clasificada, ya que es fundamental para el diseño de armas nucleares, pero algunos documentos han sido desclasificados.
| Nuclide | Media vida (y) | Masa crítica (kg) | Diámetro (cm) | Ref. |
|---|---|---|---|---|
| uranio-233 | 159.200 | 15 | 11 | |
| uranio-235 | 703.800.000 | 52 | 17 | |
| neptunium-236 | 154.000 | 7 | 8.7 | |
| neptunium-237 | 144.000 | 60 | 18 | |
| plutonio-238 | 87,7 | 9.04-10.07 | 9.5–9.9 | |
| plutonio-239 | 24,110 | 10 | 9.9 | |
| plutonio-240 | 6561 | 40 | 15 | |
| plutonio-241 | 14.3 | 12 | 10,5 | |
| plutonio-242 | 375.000 | 75 a 100 | 19 a 21 | |
| americium-241 | 432.2 | 55 a 77 | 20 a 23 | |
| americium-242m | 141 | 9 a 14 | 11 a 13 | |
| americium-243 | 7370 | 180–280 | 30 a 35 | |
| curium-243 | 29.1 | 7.34 a 10 | 10 a 11 | |
| curium-244 | 18.1 | 13.5 a 30 | 12.4 a 16 | |
| curium-245 | 8500 | 9.41–12.3 | 11 a 12 | |
| curium-246 | 4760 | 39–70.1 | 18 a 21 | |
| curium-247 | 15.600,000 | 6.94 a 7.06 | 9.9 | |
| berkelium-247 | 1380 | 75,7 | 11.8-12.2 | |
| berkelium-249 | 0.9 | 192 | 16.1 a 16.6 | |
| californio-249 | 351 | 6 | 9 | |
| californio-251 | 900 | 5.46 | 8,5 | |
| californio-252 | 2.6 | 2.73 | 6.9 | |
| einsteinium-254 | 0,7555 | 9.89 | 7.1 |
La masa crítica para el uranio de grado inferior depende en gran medida del grado: con un 20 % de 235U, supera los 400 kg; con un 15 % de 235U, supera con creces los 600 kg.
La masa crítica es inversamente proporcional al cuadrado de la densidad. Si la densidad es un 1% más y la masa un 2% menos, entonces el volumen es un 3% menos y el diámetro un 1% menos. La probabilidad de que un neutrón por cm recorrido golpee un núcleo es proporcional a la densidad. De ello se deduce que un 1% más de densidad significa que la distancia recorrida antes de salir del sistema es un 1% menor. Esto es algo que debe tenerse en cuenta cuando se intentan estimaciones más precisas de las masas críticas de los isótopos de plutonio que los valores aproximados dados anteriormente, porque el plutonio metálico tiene una gran cantidad de fases cristalinas diferentes que pueden tener densidades muy variables.
Tenga en cuenta que no todos los neutrones contribuyen a la reacción en cadena. Algunos escapan y otros sufren captura radiativa.
Sea q la probabilidad de que un neutrón determinado induzca la fisión en un núcleo. Considere solo los neutrones rápidos y denote con ν el número de neutrones rápidos generados en una fisión nuclear. Por ejemplo, ν ≈ 2,5 para el uranio-235. Entonces, la criticidad ocurre cuando ν·q = 1. La dependencia de esto con la geometría, la masa y la densidad aparece a través del factor q.
Dada una sección de interacción total σ (normalmente medida en granos), el camino medio libre de un neutrón rápido es l l − − 1=nσ σ {displaystyle ell ^{-1}=nsigma } Donde n es la densidad del número nuclear. La mayoría de las interacciones están dispersando eventos, por lo que un determinado neutron obedece a un paseo aleatorio hasta que escapa del medio o causa una reacción de fisión. Mientras que otros mecanismos de pérdida no sean significativos, entonces, el radio de una masa crítica esférica es más bien dado por el producto del camino libre medio l l {displaystyle ell } y la raíz cuadrada de uno más el número de eventos de dispersión por evento de fisión (llamar esto s), ya que la distancia neta viajada en un paseo aleatorio es proporcional a la raíz cuadrada del número de pasos:
- Rc≃ ≃ l l s≃ ≃ snσ σ {displaystyle ¿Qué? {}{nsigma }
Tenga en cuenta de nuevo, sin embargo, que esto es solo una estimación aproximada.
En términos de la masa total M, la masa nuclear m, la densidad ρ y un factor fudge f que tiene en cuenta efectos geométricos y otros, la criticidad corresponde a
- 1=fσ σ ms*** *** 2/3M1/3{displaystyle 1={frac {sigma } {m{m { sqrt {s}}rho ^{2/3}M^{1/3}
lo que recupera claramente el resultado antes mencionado de que la masa crítica depende inversamente del cuadrado de la densidad.
Alternativamente, uno puede reformular esto de manera más sucinta en términos de la densidad de área de masa, Σ:
- 1=f.σ σ ms.. {displaystyle 1={frac {f'sigma } {m{m { sqrt {s}} Sigma
donde el factor f se ha reescrito como f' para tener en cuenta el hecho de que los dos valores pueden diferir según los efectos geométricos y cómo se define Σ. Por ejemplo, para una esfera sólida desnuda de 239Pu, la criticidad es de 320 kg/m2, independientemente de la densidad, y para 235U de 550 kg/m2. En cualquier caso, la criticidad depende entonces de un típico 'ver' de neutrones. una cantidad de núcleos a su alrededor tal que la densidad de área de los núcleos excede un cierto umbral.
Esto se aplica en armas nucleares de tipo implosión donde una masa esférica de material fisionable que es sustancialmente menor que una masa crítica se vuelve supercrítica aumentando muy rápidamente ρ (y por lo tanto también Σ) (ver más abajo). De hecho, los programas de armas nucleares sofisticados pueden fabricar un dispositivo funcional con menos material del que requieren los programas de armas más primitivos.
Además de las matemáticas, hay un análogo físico simple que ayuda a explicar este resultado. Considere los gases diesel expulsados por un tubo de escape. Inicialmente, los humos aparecen negros, luego, gradualmente, puede ver a través de ellos sin ningún problema. Esto no se debe a que la sección transversal de dispersión total de todas las partículas de hollín haya cambiado, sino a que el hollín se ha dispersado. Si consideramos un cubo transparente de longitud L por un lado, lleno de hollín, entonces la profundidad óptica de este medio es inversamente proporcional al cuadrado de L, y por tanto proporcional a la densidad de área de las partículas de hollín: podemos hacer que sea más fácil ver a través del cubo imaginario simplemente agrandando el cubo.
Varias incertidumbres contribuyen a la determinación de un valor preciso para las masas críticas, incluido (1) conocimiento detallado de las secciones transversales de fisión, (2) cálculo de efectos geométricos. Este último problema proporcionó una motivación significativa para el desarrollo del método Monte Carlo en física computacional por parte de Nicholas Metropolis y Stanislaw Ulam. De hecho, incluso para una esfera sólida homogénea, el cálculo exacto no es trivial. Finalmente, tenga en cuenta que el cálculo también se puede realizar asumiendo una aproximación continua para el transporte de neutrones. Esto lo reduce a un problema de difusión. Sin embargo, como las dimensiones lineales típicas no son significativamente mayores que el camino libre medio, tal aproximación es aplicable solo marginalmente.
Por último, tenga en cuenta que para algunas geometrías idealizadas, la masa crítica podría ser formalmente infinita y se utilizan otros parámetros para describir la criticidad. Por ejemplo, considere una lámina infinita de material fisionable. Para cualquier grosor finito, esto corresponde a una masa infinita. Sin embargo, la criticidad solo se logra una vez que el espesor de esta losa supera un valor crítico.
Criticidad en el diseño de armas nucleares
Hasta que se desee la detonación, un arma nuclear debe mantenerse subcrítica. En el caso de una bomba de tipo cañón de uranio, esto se puede lograr manteniendo el combustible en varias piezas separadas, cada una por debajo del tamaño crítico, ya sea porque son demasiado pequeñas o porque tienen una forma desfavorable. Para producir la detonación, las piezas de uranio se juntan rápidamente. En Little Boy, esto se logró disparando una pieza de uranio (una 'dona') por el cañón de una pistola sobre otra pieza (una 'punta'). Este diseño se conoce como arma de fisión tipo pistola.
Un arma de Pu 239 100 % pura teórica también podría construirse como un arma tipo pistola, como el diseño Thin Man propuesto por el Proyecto Manhattan. En realidad, esto no es práctico porque incluso el "grado de armas" 239Pu está contaminado con una pequeña cantidad de 240Pu, que tiene una fuerte propensión a la fisión espontánea. Debido a esto, un arma tipo pistola de tamaño razonable sufriría una reacción nuclear (predetonación) antes de que las masas de plutonio estuvieran en condiciones de que se produjera una explosión en toda regla.
En cambio, el plutonio está presente como una esfera subcrítica (u otra forma), que puede o no ser hueca. La detonación se produce al explotar una carga con forma que rodea la esfera, aumentando la densidad (y colapsando la cavidad, si está presente) para producir una configuración crítica inmediata. Esto se conoce como un arma de tipo implosión.
Importancia crítica
El evento de fisión debe liberar, en promedio, más de un neutrón libre del nivel de energía deseado para mantener una reacción en cadena, y cada uno debe encontrar otros núcleos y provocar su fisión. La mayoría de los neutrones liberados por un evento de fisión provienen inmediatamente de ese evento, pero una fracción de ellos llega más tarde, cuando los productos de fisión se desintegran, lo que puede ser en promedio de microsegundos a minutos más tarde. Esto es una suerte para la generación de energía atómica, ya que sin este retraso, 'se vuelve crítico'. sería un evento inmediatamente catastrófico, como lo es en una bomba nuclear donde ocurren más de 80 generaciones de reacciones en cadena en menos de un microsegundo, demasiado rápido para que un humano, o incluso una máquina, reaccione. Los físicos reconocen dos puntos en el aumento gradual del flujo de neutrones que son significativos: crítico, donde la reacción en cadena se vuelve autosuficiente gracias a las contribuciones de ambos tipos de generación de neutrones, y crítico rápido, donde el "rápido" inmediato; los neutrones solos sostendrán la reacción sin necesidad de los neutrones de desintegración. Las plantas de energía nuclear operan entre estos dos puntos de reactividad, mientras que por encima del punto crítico rápido está el dominio de las armas nucleares y algunos accidentes de energía nuclear, como el desastre de Chernobyl.
Contenido relacionado
Superplasticidad
Renault en la Fórmula Uno
El universo en pocas palabras