Máquina térmica de Carnot

Sección transversal axial del motor de calor de Carnot. En este diagrama, abcd es un vaso cilíndrico, cd es un pistón móvil, y A y B son cuerpos de temperatura constantes. El buque puede ponerse en contacto con el cuerpo o retirarse de ambos (como está aquí).

Una máquina térmica de Carnot es una máquina térmica que funciona según el ciclo de Carnot. El modelo básico de este motor fue desarrollado por Nicolas Léonard Sadi Carnot en 1824. Benoît Paul Émile Clapeyron amplió gráficamente el modelo de motor de Carnot en 1834 y Rudolf Clausius lo exploró matemáticamente en 1857, trabajo que condujo al concepto termodinámico fundamental de la entropía. El motor de Carnot es el motor térmico más eficiente que es teóricamente posible. La eficiencia depende únicamente de las temperaturas absolutas de los depósitos de calor frío y caliente entre los que opera.

Un motor térmico actúa transfiriendo energía de una región cálida a una región fría del espacio y, en el proceso, convierte parte de esa energía en trabajo mecánico. El ciclo también puede invertirse. Una fuerza externa puede trabajar sobre el sistema y, en el proceso, puede transferir energía térmica de un sistema más frío a uno más caliente, actuando así como un refrigerador o una bomba de calor en lugar de un motor térmico.

Todo sistema termodinámico existe en un estado particular. Un ciclo termodinámico ocurre cuando un sistema pasa por una serie de estados diferentes y finalmente regresa a su estado inicial. En el proceso de pasar por este ciclo, el sistema puede realizar trabajo sobre su entorno, actuando así como un motor térmico.

Diagrama de Carnot

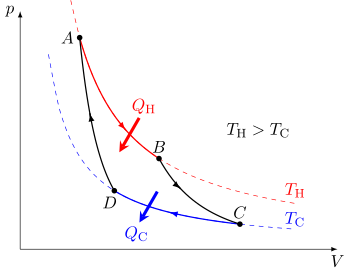
En el diagrama adyacente, de la obra de Carnot de 1824, Reflexiones sobre la fuerza motriz del fuego, hay "dos cuerpos A y B, mantenidas cada una a una temperatura constante, siendo la de A superior a la de B. Estos dos cuerpos a los que podemos dar, o de los que podemos sacar el calor sin hacer variar sus temperaturas, ejercen las funciones de dos depósitos ilimitados de calórico. Llamaremos al primero el horno y al segundo el refrigerador.” Carnot explica entonces cómo podemos obtener fuerza motriz, es decir, “trabajo”, llevando una cierta cantidad de calor del cuerpo A al cuerpo B. También actúa como enfriador y, por lo tanto, también puede actuar como refrigerador.

Diagrama moderno

Esquema de motor Carnot (moderna) - donde una cantidad de calor Q_H flujos de alta temperatura T_H horno a través del fluido del "cuerpo de trabajo" (sustancia de trabajo) y el calor restante Q_C flujos hacia el fregadero frío T_C, obligando así a la sustancia de trabajo a hacer trabajos mecánicos W sobre el entorno, mediante ciclos de contracciones y expansiones.

La imagen anterior muestra el diagrama original de pistón y cilindro utilizado por Carnot al hablar de su motor ideal. La figura de la derecha muestra un diagrama de bloques de una máquina térmica genérica, como la máquina de Carnot. En el diagrama, el "cuerpo de trabajo" (sistema), un término introducido por Clausius en 1850, puede ser cualquier cuerpo fluido o de vapor a través del cual se puede introducir o transmitir calor Q para producir trabajo. Carnot había postulado que el cuerpo fluido podía ser cualquier sustancia capaz de expandirse, como vapor de agua, vapor de alcohol, vapor de mercurio, un gas permanente, aire, etc. Aunque en esos primeros años, los motores tenían varias configuraciones., típicamente Q_H fue suministrado por una caldera, donde el agua se hirvió sobre un horno; Q_C normalmente se eliminaba con un chorro de agua fría en forma de un condensador ubicado en una parte separada del motor. El trabajo de salida, W, se transmite por el movimiento del pistón cuando se utiliza para hacer girar un brazo de manivela, que a su vez se usaba normalmente para accionar una polea a fin de sacar el agua de las aguas inundadas. minas de sal. Carnot definió el trabajo como “peso levantado a través de una altura”.

Ciclo de Carnot

Figura 1: Un ciclo de Carnot ilustrado en un diagrama de PV para ilustrar el trabajo realizado.

Figura 2: Un ciclo de Carnot actuando como un motor de calor, ilustrado en un diagrama de temperatura-entropía. El ciclo tiene lugar entre un embalse caliente a temperatura T_H y un depósito frío a temperatura T_C. El eje vertical es temperatura, el eje horizontal es entropía.

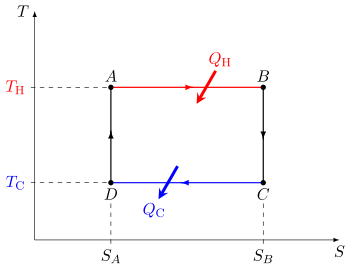
El ciclo de Carnot cuando actúa como máquina térmica consta de los siguientes pasos:

1. Ampliación isotérmica reversible del gas a la temperatura "caliente", T_H (adicionamiento térmico o absorción). Durante este paso (A a B) el gas se permite expandir y funciona en el entorno. La temperatura del gas (el sistema) no cambia durante el proceso, por lo que la expansión es isotérmica. La expansión del gas es impulsada por la absorción de energía térmica Q_H y de entropía Δ Δ SH=QH/TH{displaystyle Delta S_{text{H}=Q_{text{H}/T_{H}}} del depósito de alta temperatura.
2. Isentropic (reversible adiabático) expansión del gas (producto de trabajo histrópico). Para este paso (B a C) el pistón y el cilindro se supone que están aislados térmicamente, por lo que no ganan ni pierden calor. El gas continúa expandiendo, haciendo trabajo en el entorno y perdiendo una cantidad equivalente de energía interna. La expansión del gas hace que se enfríe a la temperatura "frío", T_C. La entropía sigue sin cambiar.
3. Compresión isotérmica reversible del gas a la temperatura "frío", T_C. (Rechazo de calor esotérmico) ()C a D) Ahora el gas está expuesto al depósito de temperatura fría, mientras que los alrededores trabajan en el gas comprimiéndolo (como a través de la compresión de retorno de un pistón), mientras que causa una cantidad de calor de desperdicio Q_C 0 (con la convención de signos estándar para el calor) y de la entropía <math alttext="{displaystyle Delta S_{text{C}}=Q_{text{C}}/T_{text{C}}Δ Δ SC=QC/TC.0{displaystyle Delta S_{text{C}}=Q_{text{C}/T_{text{C} {f} {f}} {f}}} {f}} {f}} {f}}} {f}}} {f}}}}}}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}} {f}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}<img alt="{displaystyle Delta S_{text{C}}=Q_{text{C}}/T_{text{C}} para salir del gas al depósito de baja temperatura. (En magnitud, esta es la misma cantidad de entropía absorbida en el paso 1. La entropía disminuye en la compresión isotérmica ya que la multiplicidad del sistema disminuye con el volumen.) En términos de magnitud, el trabajo de recompresión realizado por los alrededores en este paso es menor que el trabajo realizado en el entorno en el paso 1 porque se produce a una presión inferior debido a la temperatura inferior (es decir, la resistencia a la compresión es menor bajo paso 3 que la fuerza de expansión bajo paso 1).
4. Compresión istrópica del gas (insumo de trabajo histrópico). ()D a A) Una vez más se supone que el pistón y el cilindro están aislados térmicamente y se elimina el depósito de temperatura fría. Durante este paso, los alrededores continúan trabajando para comprimir el gas y el aumento de temperatura y presión ahora que se ha eliminado el disipador de calor. Este trabajo adicional aumenta la energía interna del gas, comprime y hace que la temperatura aumente T_H. La entropía sigue sin cambiar. En este punto el gas está en el mismo estado que al comienzo del paso 1.

Teorema de Carnot

Motores ideales reales (izquierda) en comparación con el ciclo Carnot (derecha). La entropía de un material real cambia con temperatura. Este cambio se indica por la curva en un diagrama T-S. Para esta figura, la curva indica un equilibrio líquido de vapor (Ver ciclo de Rankine). Los sistemas irreversibles y las pérdidas de calor (por ejemplo, debido a la fricción) impiden que el ideal tenga lugar a cada paso.

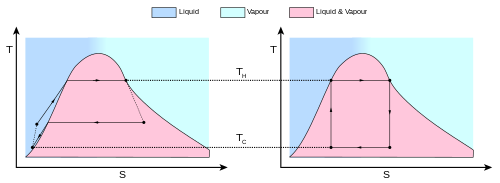
El teorema de Carnot es una declaración formal de este hecho: Ningún motor que funcione entre dos depósitos de calor puede ser más eficiente que un motor de Carnot que funcione entre los mismos depósitos.

.. I=WQH=1− − TCTH{displaystyle eta {fnMicroc} {fnMicrosoft Sans Serif} {H}}=1-{frac} {fnMicrom} {C} {fn} {fn}}} {fn}}} {fn}}}} {}}} {fn}}}}}}} {}}}}}}} {}}}}} {}}} {}}}} {}}}} {}}} {}}}}} {}}}}}} {}}}}}}}} {}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}} {}}} {} {}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Explicación
Esta máxima eficiencia .. I{displaystyle eta _{text{I}} se define como arriba:

W es el trabajo realizado por el sistema (energía saliendo del sistema como trabajo),

QH{displaystyle Q_{text{H}} es el calor puesto en el sistema (energía térmica entrando en el sistema),

TC{displaystyle T_{text{C}} es la temperatura absoluta del embalse frío, y

TH{displaystyle T_{text{H}} es la temperatura absoluta del embalse caliente.

Un corolario del teorema de Carnot establece que: Todos los motores reversibles que operan entre los mismos depósitos de calor son igualmente eficientes.

Se demuestra fácilmente que la eficiencia η es máxima cuando todo el proceso cíclico es un proceso reversible. Esto significa que la entropía total del sistema y el entorno (las entropías del horno caliente, el "fluido de trabajo" de la máquina térmica y el sumidero frío) permanece constante cuando el "fluido de trabajo" se mantiene constante. completa un ciclo y vuelve a su estado original. (En el caso general y más realista de un proceso irreversible, la entropía total de este sistema combinado aumentaría).

Dado que el "fluido de trabajo" vuelve al mismo estado después de un ciclo, y la entropía del sistema es una función de estado, el cambio en la entropía del "fluido de trabajo" sistema es 0. Por lo tanto, implica que el cambio de entropía total del horno y el fregadero es cero, para que el proceso sea reversible y la eficiencia del motor sea máxima. Esta derivación se lleva a cabo en la siguiente sección.

El coeficiente de rendimiento (COP) de la máquina térmica es el recíproco de su eficiencia.

Eficiencia de motores térmicos reales

Para una máquina térmica real, el proceso termodinámico total es generalmente irreversible. El fluido de trabajo vuelve a su estado inicial después de un ciclo y, por lo tanto, el cambio de entropía del sistema de fluido es 0, pero la suma de los cambios de entropía en el depósito caliente y frío en este proceso cíclico es mayor que 0.

La energía interna del fluido es también una variable estatal, por lo que su cambio total en un ciclo es 0. Así que el trabajo total realizado por el sistema W es igual al calor neto puesto en el sistema, la suma de QH{displaystyle Q_{text{H}} ■ 0 tomada y el calor de los residuos QC{displaystyle Q_{text{C}} 0 dado fuera:

W=Q=QH+QC{displaystyle ¿Qué?

()2)

Para motores reales, las etapas 1 y 3 del ciclo de Carnot, en las que el calor es absorbido por el "fluido de trabajo" del reservorio caliente, y liberados por éste al reservorio frío, respectivamente, ya no son idealmente reversibles, y existe un diferencial de temperatura entre la temperatura del reservorio y la temperatura del fluido mientras se produce el intercambio de calor.

Durante la transferencia de calor del depósito caliente TH{displaystyle T_{text{H}} al fluido, el fluido tendría una temperatura ligeramente inferior a la TH{displaystyle T_{text{H}}, y el proceso para el líquido puede no permanecer necesariamente estermal. Vamos Δ Δ SH{displaystyle Delta S_{text{H}} ser el cambio total entropía del fluido en el proceso de ingesta de calor.

Δ Δ SH=∫ ∫ QdentrodQHT{displaystyle Delta S_{text{H}=int {fnK} {fnK}} {fnK}} {fnK}}}}} {f}}} {f}} {fnf}}}} {fnfnK}}}} {fnK}}}}}}}}

()3)

donde la temperatura del líquido T es siempre ligeramente menor que TH{displaystyle T_{text{H}}En este proceso.

Entonces, uno obtendría:

QHTH=∫ ∫ dQHTH≤ ≤ Δ Δ SH{displaystyle {frac {f} {f}} {f}}}={f}}} {f}} {f}} {f}}} {f}}} {f}}}} {f}}} {f}}} {f}}}} {f}f}f}}}}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}} {f}}}} {f} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}f}}}}f}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}\\\\f}}}}}}}}} {cH} {fnh}}}mfnh} {fnh}}}leq}} Delta S_{text{H}}

()4)

Del mismo modo, en el momento de la inyección de calor del fluido al depósito frío uno tendría, por la magnitud del cambio total de entropía Δ Δ SC{displaystyle Delta S_{text{C}}}0 del fluido en el proceso de expulsión del calor:

<math alttext="{displaystyle Delta S_{text{C}}geqslant {frac {Q_{text{C}}}{T_{text{C}}}}Δ Δ SC⩾ ⩾ QCTC.0{displaystyle Delta S_{text{C}gqslant {frac {Q_{text{C}}{T_{text{C}}}}} {f}}}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}}}}}} {<img alt="{displaystyle Delta S_{text{C}}geqslant {frac {Q_{text{C}}}{T_{text{C}}}}

()5)

donde, durante este proceso de transferencia de calor al depósito frío, la temperatura del fluido T es siempre un poco mayor que TC{displaystyle T_{text{C}}.

Aquí solo hemos considerado la magnitud del cambio de entropía. Dado que el cambio total de entropía del sistema fluido para el proceso cíclico es 0, debemos tener

Δ Δ SH+Δ Δ SC=Δ Δ Sciclo=0{displaystyle Delta S_{text{H}+ Delta S_{text{C}= Delta S_{text{cycle}=0}

()6)

Las tres ecuaciones anteriores se combinan para dar:

− − QCTC⩾ ⩾ QHTH{displaystyle -{frac {fnK} {f}} {fnK}}} {f}}}}} {f}}}} {f}}} {f}}}} {f}}}}}}}}} {f}}}} {f}}}}} {f}}}}}} {f}}}}}}}}}}}}}}

()7)

Las ecuaciones (2) y (7) se combinan para dar

WQH≤ ≤ 1− − TCTH{displaystyle {frac {W}{text{H}}leq 1-{frac {T_{text{C} {T_{H}}} {f}} {f}} {f}} {f}}} {f}}}} {f}}}} {f}}}}}}}} {f}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

()8)

Por lo tanto,

.. ≤ ≤ .. I{displaystyle eta leq eta _{I}}

()9)

Donde .. =WQH{displaystyle eta ={frac {W}{Q_{H}}} es la eficiencia del motor real, y .. I{displaystyle eta _{text{I}} es la eficiencia del motor Carnot trabajando entre los mismos dos embalses a las temperaturas TH{displaystyle T_{text{H}} y TC{displaystyle T_{text{C}}. Para el motor Carnot, todo el proceso es "reversible", y Ecuación (7) es una igualdad. Por lo tanto, la eficiencia del motor real es siempre menos que el motor ideal de Carnot.

Ecuación7) significa que la entropía total del sistema y el entorno (el fluido y los dos embalses) aumenta para el motor real, porque (en un análisis basado en el entorno) la ganancia entropía del embalse frío como QC{displaystyle Q_{text{C}} fluye hacia ella a temperatura fija TC{displaystyle T_{text{C}}, es mayor que la pérdida de entropía del embalse caliente como QH{displaystyle Q_{text{H}} lo deja a su temperatura fija TH{displaystyle T_{text{H}}. La desigualdad en la ecuación (7) es esencialmente la declaración del teorema de Clausius.

Según el segundo teorema, "La eficiencia del motor de Carnot es independiente de la naturaleza de la sustancia de trabajo".

La máquina de Carnot y Rudolf Diesel

En 1892, Rudolf Diesel patentó un motor de combustión interna inspirado en el motor de Carnot. Diesel sabía que una máquina de Carnot es un ideal que no se puede construir, pero pensó que había inventado una aproximación funcional. Su principio no era sólido, pero en su lucha por implementarlo desarrolló el motor práctico que lleva su nombre.

El problema conceptual era cómo lograr la expansión isotérmica en un motor de combustión interna, ya que quemar combustible a la temperatura más alta del ciclo solo elevaría aún más la temperatura. La solución patentada de Diesel fue: haber alcanzado la temperatura más alta simplemente comprimiendo el aire, agregar una pequeña cantidad de combustible a un ritmo controlado, de modo que el calentamiento causado por la quema del combustible se contrarrestaría con el enfriamiento causado por la expansión del aire como el pistón se movió. Por tanto, todo el calor del combustible se transformaría en trabajo durante la expansión isotérmica, como exige el teorema de Carnot.

Para que la idea funcione, una pequeña masa de combustible tendría que quemarse en una gran masa de aire. Diesel propuso por primera vez un motor en funcionamiento que comprimiría el aire a 250 atmósferas a 800 °C, luego ciclaría a una atmósfera a 20 °C. Sin embargo, esto estaba mucho más allá de las capacidades tecnológicas de la época, ya que implicaba una relación de compresión de 60:1. Tal motor, si se hubiera construido, habría tenido una eficiencia del 73%. (En contraste, las mejores máquinas de vapor de su época alcanzaron el 7%).

En consecuencia, Diesel buscó llegar a un acuerdo. Calculó que, si redujera la presión máxima a 90 atmósferas menos ambiciosas, sacrificaría solo el 5% de la eficiencia térmica. Buscando apoyo financiero, publicó "Teoría y construcción de un motor térmico racional para tomar el lugar del motor de vapor y todos los motores de combustión actualmente conocidos" (1893). Respaldado por la opinión científica, incluido Lord Kelvin, obtuvo el respaldo de Krupp y Maschinenfabrik Augsburg. Se aferró al ciclo de Carnot como símbolo. Pero años de trabajo práctico no lograron ni podrían haber logrado un motor de combustión isotérmico, ya que requiere una cantidad de aire tan enorme que no puede desarrollar la potencia suficiente para comprimirlo. Además, la inyección de combustible controlada resultó no ser un asunto fácil.

Aún así, evolucionó lentamente durante 25 años para convertirse en un práctico motor de aire de alta compresión, su combustible se inyectaba cerca del final de la carrera de compresión y se encendía por el calor de la compresión, en una palabra, el motor diésel. Hoy su eficiencia es del 40%.