Máquina post-Turing
Una máquina post-Turing es una "formulación de programa" de un tipo de máquina de Turing, que comprende una variante del modelo de cálculo equivalente a Turing de Emil Post. El modelo de Post y el modelo de Turing, aunque muy similares entre sí, se desarrollaron de forma independiente. El artículo de Turing se recibió para su publicación en mayo de 1936, seguido por el del Post en octubre. Una máquina Post-Turing utiliza un alfabeto binario, una secuencia infinita de ubicaciones de almacenamiento binario y un lenguaje de programación primitivo con instrucciones para el movimiento bidireccional entre las ubicaciones de almacenamiento y la alteración de su contenido uno a la vez. Los nombres "Programa Post-Turing" y "Post-máquina de Turing" fueron utilizados por Martin Davis en 1973-1974 (Davis 1973, p. 69ff). Más tarde, en 1980, Davis utilizó el nombre "programa Turing-Post" (Davis, en Steen pág. 241).
1936: Postmodelo
En su artículo de 1936 "Procesos combinatorios finitos: formulación 1", Emil Post describió un modelo que, según conjeturó, es "lógicamente equivalente a la recursividad".
El modelo de cálculo de Post se diferencia del modelo de la máquina de Turing en una mayor "atomización" de los actos un ser humano "computadora" realizaría durante un cálculo.
El modelo de Post emplea un "espacio de símbolos" que consiste en una "secuencia infinita bidireccional de espacios o cajas", cada caja capaz de estar en cualquiera de dos condiciones posibles, a saber, "marcada"; (como por un solo trazo vertical) y "sin marcar" (vacío). Inicialmente, un número finito de casillas están marcadas y el resto sin marcar. Un "trabajador" entonces es moverse entre las cajas, estar dentro y operar en una sola caja a la vez, de acuerdo con un "conjunto de direcciones" finito y fijo; (instrucciones), que están numeradas en orden (1,2,3,...,n). Comenzando en un recuadro "señalado como punto de partida", el trabajador debe seguir el conjunto de instrucciones una por una, comenzando con la instrucción 1.
Hay cinco operaciones primitivas diferentes que el trabajador puede realizar:
- a) Marcar la caja en la que está, si está vacía
- b) Borrar la marca en la caja en la que está, si está marcada
- c) Mover a la caja a la derecha
- d) Mover a la caja a la izquierda
- e) Determinar si la caja en la que está, está o no está marcada.
Entonces, la i th "dirección" (instrucción) dada al trabajador debe ser de una de las siguientes formas:
- Operación de datos Oi [Oi a), b), c) o d)] y luego seguir la dirección ji
- Operación de datos e) y según la respuesta es sí o no correspondiente seguir dirección ji. o Ji.
- Para..
(El texto con sangría y cursiva anterior es el mismo que el original). La publicación comenta que esta formulación se encuentra "en sus etapas iniciales" de desarrollo, y menciona varias posibilidades para una "mayor flexibilidad" en su "forma definitiva" final, incluyendo
- reemplazando el infinito de cajas por un espacio de símbolos extensible finito, "extendiendo las operaciones primitivas para permitir la extensión necesaria del espacio de símbolo finito dado a medida que el proceso avanza",
- usando un alfabeto de más de dos símbolos, "tener más de una manera de marcar una caja",
- introduciendo "objetos físicos para servir como punteros, que el trabajador puede identificar y moverse de caja a caja".
1947: reducción formal de Post de las 5 tuplas de Turing a 4 tuplas
Como se menciona brevemente en el artículo La máquina de Turing, Post, en su artículo de 1947 (Insolvabilidad recursiva de un problema de Thue) atomizó las 5 tuplas de Turing en 4 tuplas:
- "Nuestros cuádruples son quintuplets en el desarrollo de Turing. Es decir, donde nuestra instrucción estándar ordena una impresión (sobreimpresión) o movimiento, izquierda o derecha, la instrucción estándar de Turing siempre ordena una impresión y a motion, right, left, or none" (nota 12, Undecidable, pág. 300)
Al igual que Turing, definió el borrado como imprimir un símbolo "S0". Y así su modelo admitía cuatrillizos de sólo tres tipos (cf. Indecidible, p. 294):
- qi Sj L ql,
- qi Sj R ql,
- qi Sj Sk ql
En ese momento todavía conservaba la convención de la máquina de estados de Turing: no había formalizado la noción de una supuesta ejecución secuencial de pasos hasta una prueba específica de un símbolo "ramificado" 34; la ejecución en otro lugar.
1954, 1957: modelo Wang
Para una reducción aún mayor (a solo cuatro instrucciones) del modelo Wang presentado aquí, consulte Wang B-machine.
A menudo se cita a Wang (1957, pero presentado a la ACM en 1954) (cf. Minsky (1967), p. 200) como la fuente de la "formulación del programa" de máquinas de Turing de cinta binaria utilizando instrucciones numeradas del conjunto
- escribir 0
- escribir 1
- movimiento izquierda
- movimiento derecho
- si escanea 0 entonces ir a la instrucción i
- si escanea 1 entonces ir a la instrucción j
Cualquier máquina de Turing de cinta binaria se convierte fácilmente en un programa equivalente "Wang" usando las instrucciones anteriores.
1974: primer modelo Davis
Martin Davis era un estudiante universitario de Emil Post. Junto con Stephen Kleene completó su doctorado. bajo Alonzo Church (Davis (2000) 1ª y 2ª notas al pie p. 188).
Presentó el siguiente modelo en una serie de conferencias en el Instituto Courant de la Universidad de Nueva York en 1973-1974. Este es el modelo al que Davis aplicó formalmente el nombre de "máquina post-Turing" con su "lenguaje post-Turing". Se supone que las instrucciones se ejecutan secuencialmente (Davis 1974, p. 71):
1978: segundo modelo de Davis
El siguiente modelo aparece como un ensayo ¿Qué es un cálculo? en las páginas 241–267 de Steen. Por alguna razón, Davis ha cambiado el nombre de su modelo a "máquina de Turing-Post" (con un retroceso en la página 256.)
En el siguiente modelo, Davis asigna los números "1" a la "marca/barra" de la publicación y "0" al cuadrado en blanco. Para citar a Davis: “Ahora estamos listos para presentar el lenguaje de programación Turing-Post. En este idioma existen siete tipos de instrucciones:
- "PRINT 1
- "PRINT 0
- "Correcto"
- "GO LEFT
- "GO TO STEP IF 1 IS SCANNED
- "GO TO STEP IF 0 IS SCANNED
- "STOP"
"Un programa de Turing-Post es entonces una lista de instrucciones, cada una de las cuales es de uno de estos siete tipos. Por supuesto, en un programa real, la letra i en un paso del quinto o sexto tipo debe reemplazarse con un número definido (entero positivo)." (Davis en Steen, pág. 247).
1994 (segunda edición): modelo de programa Post-Turing de Davis-Sigal-Weyuker
"Aunque la formulación de Turing que hemos presentado tiene un espíritu más cercano a la dada originalmente por Emil Post, fue el análisis de Turing del cálculo lo que hizo que esta formulación pareciera tan apropiada. Este lenguaje ha jugado un papel fundamental en la informática teórica." (Davis et al. (1994) pág. 129)
Este modelo permite la impresión de múltiples símbolos. El modelo permite B (en blanco) en lugar de S0. La cinta es infinita en ambas direcciones. O la cabeza o la cinta se mueven, pero sus definiciones de DERECHA e IZQUIERDA siempre especifican el mismo resultado en cualquier caso (Turing usó la misma convención).
- PRINT σ;Reemplazar símbolo escaneado con σ
- IF σ GOTO L;IF símbolo escaneado es σ THEN ir a "el primero" instrucción etiquetada L
- DERECHO;Scan cuadrado inmediatamente derecho del cuadrado actualmente escaneado
- LEFT;Scan cuadrado inmediatamente izquierda del cuadrado actualmente escaneado
Este modelo se reduce a las versiones binarias { 0, 1 } presentadas anteriormente, como se muestra aquí:
- PRINT 0 = ERASE;Reemplazar el símbolo escaneado con 0 = B = BLANK
- PRINT 1; Reemplazar el símbolo escaneado con 1
- IF 0 GOTO L;IF símbolo escaneado es 0 A continuación ir a "la primera" instrucción etiquetada L
- IF 1 GOTO L;IF símbolo escaneado es 1 A continuación ir a "la primera" instrucción etiquetada L
- DERECHO;Scan cuadrado inmediatamente derecho del cuadrado actualmente escaneado
- LEFT;Scan cuadrado inmediatamente izquierda del cuadrado actualmente escaneado
Ejemplos de la máquina de Post-Turing
Atomizar quintuplicados de Turing en una secuencia de instrucciones post-Turing
La siguiente "reducción" (descomposición, atomización), desde 5 tuplas de Turing de 2 símbolos hasta una secuencia de instrucciones Post-Turing de 2 símbolos, se puede encontrar en Minsky (1961). Afirma que esta reducción a "un programa... una secuencia de Instrucciones" está en el espíritu de la máquina B de Hao Wang (cursiva en el original, cf. Minsky (1961) p. 439).
(La reducción de Minsky a lo que él llama "una subrutina" da como resultado 5 en lugar de 7 instrucciones Post-Turing. No atomizó Wi0: "Escriba el símbolo Si0; vaya al nuevo estado Mi0" y Wi1: "Escriba el símbolo Si1; vaya al nuevo estado Mi1". El siguiente método atomiza aún más Wi0 y Wi1; en todos los demás aspectos, los métodos son idénticos).
Esta reducción de 5 tuplas de Turing a instrucciones posteriores a Turing puede no resultar en una solución "eficiente". Programa post-Turing, pero será fiel al programa Turing original.
En el siguiente ejemplo, cada 5-tupla de Turing del castor ocupado de 2 estados se convierte en
- un "golpe" condicional inicial (goto, rama), seguido por
- 2 instrucciones de cinta para el caso "0" – Imprimir o borrar o Ninguno, seguido de izquierda o derecha o ninguno, seguido por
- un "salto" incondicional para el caso "0" a su siguiente instrucción
- 2 instrucciones de cinta adhesiva para el caso "1" – Imprimir o borrar o Ninguno, seguido de izquierda o derecha o ninguno, seguido por
- un "salto" incondicional para el caso "1" a su siguiente instrucción
para un total de 1 + 2 + 1 + 2 + 1 = 7 instrucciones por estado de Turing.
Por ejemplo, el castor ocupado de 2 estados "" El estado de Turing, escrito como dos líneas de 5 tuplas, es:
| Configuración m inicial (Estado de medición) | Símbolo de cinta | Operación de impresión | Moción de la cinta | Configuración m final (Estado de medición) |
|---|---|---|---|---|
| A | 0 | P | R | B |
| A | 1 | P | L | B |
La tabla representa solo una "instrucción" de Turing, pero vemos que consta de dos líneas de 5 tuplas, una para el caso "símbolo de cinta debajo del encabezado = 1" , el otro para el caso "símbolo de cinta debajo del encabezado = 0". Turing observó (Indecidible, p. 119) que las dos columnas de la izquierda – "m-configuration" y "símbolo" – representan la "configuración" actual de la máquina; – su estado, que incluye tanto la Cinta como la Tabla en ese instante, y las últimas tres columnas son su "comportamiento" posterior. Como la máquina no puede estar en dos "estados" inmediatamente, la máquina debe "ramificar" a una configuración u otra:
| Primera m-configuración y símbolo S | Operación de impresión | Moción de la cinta | Configuración m final |
|---|---|---|---|
| S=0 → | P → | R → | B |
| → A c) | |||
| S=1 → | P → | L → | B |
Después de la "rama de configuración" (J1 xxx) o (J0 xxx) la máquina sigue uno de los dos "comportamientos" siguientes. Enumeramos estos dos comportamientos en una línea y los numeramos (o etiquetamos) de forma secuencial (única). Debajo de cada salto (rama, ir a) colocamos su "número" (dirección, ubicación):
| Inicial m-configuración " símbolo S | Operación de impresión | Moción de la cinta | Caso final de m-configuración S=0 | Operación de impresión | Moción de la cinta | Caso final de m-configuración S=1 | |
|---|---|---|---|---|---|---|---|
| Si S=0 entonces: | P | R | B | ||||
| → A c) | |||||||
| Si S=1 entonces: | P | L | B | ||||
| instrucción | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Post-Turing instruction | J1 | P | R | J | P | L | J |
| saltar a la instrucción | 5 | B | B |
Según las convenciones de la máquina Post-Turing, cada una de las instrucciones Imprimir, Borrar, Izquierda y Derecha consta de dos acciones:
- Aplicación: Entonces...
- Medida de la tabla: vaya a la siguiente instrucción en secuencia
Y según las convenciones de la máquina de Post-Turing, los "saltos" J0xxx, J1xxx constan de dos acciones:
- Aplicación: ver el símbolo en la cinta bajo la cabeza
- Medida del cuadro: Si el símbolo es 0 (1) y J0 (J1), entonces vaya a xxx más ir a la siguiente instrucción en secuencia
Y según las convenciones de la máquina Post-Turing, el "salto" Jxxx consta de una única acción, o si queremos regularizar la secuencia de 2 acciones:
- Aplicación: ver el símbolo en la cinta bajo la cabeza
- Medida del cuadro: Si el símbolo es 0 entonces ir a xxx si el símbolo es 1 entonces ir a xxx.
¿Cuáles y cuántos saltos son necesarios? El salto incondicional Jxxx es simplemente J0 seguido inmediatamente por J1 (o viceversa). Wang (1957) también demuestra que sólo se requiere un salto condicional, es decir, J0xxx o J1xxx. Sin embargo, con esta restricción, resulta difícil escribir instrucciones para la máquina. A menudo sólo se utilizan dos, es decir.
- {} J0xxx, J1xxx
- {} J1xxx, Jxxx
- {} J0xxx, Jxxx
pero el uso de los tres { J0xxx, J1xxx, Jxxx } elimina instrucciones adicionales. En el ejemplo de Busy Beaver de 2 estados, usamos solo { J1xxx, Jxxx}.
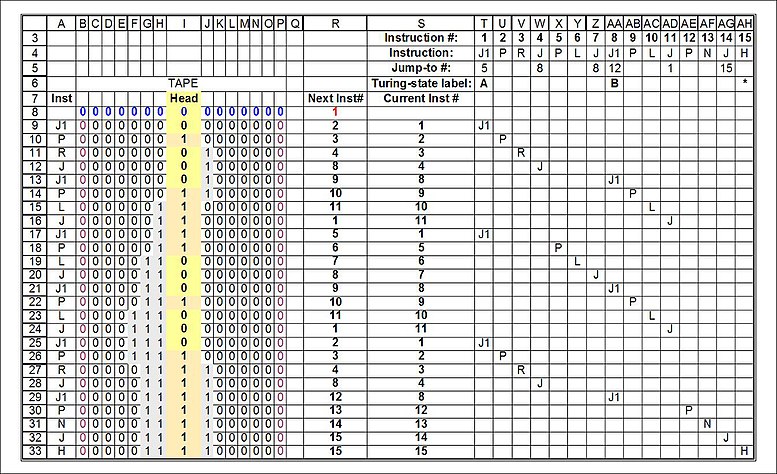
Castor ocupado de 2 estados
La misión del castor ocupado es imprimir tantos como sea posible antes de detenerse. La "Impresión" La instrucción escribe un 1, el comando "Borrar" La instrucción (no utilizada en este ejemplo) escribe un 0 (es decir, es lo mismo que P0). La cinta se mueve "Izquierda" o "Derecho" (es decir, la "cabeza" está estacionaria).
Tabla de estados para un castor ocupado de máquina de Turing de 2 estados:
| Símbolo de cinta | Estado actual A | Estado actual B | ||||
|---|---|---|---|---|---|---|
| Escribir símbolo | Mueve la cinta | Siguiente estado | Escribir símbolo | Mueve la cinta | Siguiente estado | |
| 0 | 1 | R | B | 1 | L | A |
| 1 | 1 | L | B | 1 | N | H |
Instrucciones para la versión Post-Turing de un castor ocupado de 2 estados: observe que todas las instrucciones estén en la misma línea y en secuencia. Esta es una desviación significativa del modelo de "Turing" versión y tiene el mismo formato que lo que se llama un "programa informático":
| Instrucción # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instrucción | J1 | P | R | J | P | L | J | J1 | P | L | J | P | N | J | H |
| Jump-to | 5 | 8 | 8 | 12 | 1 | 15 | |||||||||
| etiqueta Turing-state | A | B | H |
Como alternativa, podríamos escribir la tabla como una cadena. El uso de "separadores de parámetros" ":" y separadores de instrucciones "," son enteramente de nuestra elección y no aparecen en el modelo. No hay convenciones (pero consulte Booth (1967) p. 374, y Boolos y Jeffrey (1974, 1999) p. 23), para obtener algunas ideas útiles sobre cómo combinar las convenciones del diagrama de estados con las instrucciones, es decir, usar flechas para indicar el destino de los saltos). En el ejemplo inmediatamente siguiente, las instrucciones son secuenciales comenzando desde "1", y los parámetros/"operandos" se consideran parte de sus instrucciones/"códigos de operación":
- J1:5, P, R, J:8, P, L, J:8, J1:12, P, L, J1:1, P, N, J:15, H