Mapa logístico

El mapa logístico es un mapeo polinomial (equivalente a una relación de recurrencia) de grado 2, a menudo referido como un ejemplo arquetípico de cómo puede surgir un comportamiento caótico y complejo a partir de ecuaciones dinámicas no lineales muy simples.. El mapa fue popularizado en un artículo de 1976 por el biólogo Robert May, en parte como un modelo demográfico de tiempo discreto análogo a la ecuación logística escrita por Pierre François Verhulst. Matemáticamente, el mapa logístico se escribe

xn+1=rxn()1− − xn){displaystyle x_{n+1}=rx_{n}left(1-x_{n}right)}

()1)

donde x_n es un número entre cero y uno, que representa la proporción de población a la máxima población posible. Esta ecuación de diferencia no lineal pretende capturar dos efectos:

• reproducción donde la población aumentará a un ritmo proporcional a la población actual cuando el tamaño de la población sea pequeño.
• hambre (mortalidad dependiente de la densidad) donde la tasa de crecimiento disminuirá a una tasa proporcional al valor obtenido al tomar la "capacidad de cuidado" teórica del medio ambiente menos la población actual.

Los valores usuales de interés para el parámetro r son aquellos en el intervalo [0, 4], de modo que x_n permanezca delimitado en [ 0, 1]. El caso r = 4 del mapa logístico es una transformación no lineal tanto del mapa de desplazamiento de bits como del μ = 2 caso del mapa de la tienda. Si r > 4 esto conduce a tamaños de población negativos. (Este problema no aparece en el modelo anterior de Ricker, que también presenta una dinámica caótica). También se pueden considerar valores de r en el intervalo [−2, 0], de modo que x_n permanece delimitado en [−0.5, 1.5].

Características del mapa

Comportamiento dependiente de r

La siguiente imagen muestra el contenido de amplitud y frecuencia de algunas iteraciones de mapas logísticos para valores de parámetros que van de 2 a 4.

Al variar el parámetro r, se observa el siguiente comportamiento:

Evolución de diferentes condiciones iniciales como función r

• Con r entre 0 y 1, la población eventualmente morirá, independiente de la población inicial.
• Con r entre 1 y 2, la población se acercará rápidamente al valor r − 1/r, independiente de la población inicial.
• Con r entre 2 y 3 años, la población eventualmente se acercará al mismo valor r − 1/r, pero primero fluctuará alrededor de ese valor por algún tiempo. La tasa de convergencia es lineal, excepto para r = 3, cuando es dramáticamente lento, menos que lineal (ver memoria de Bifurcación).
• Con r entre 3 y 1 +√6 ■ 3.44949 la población se acercará a oscilaciones permanentes entre dos valores. Estos dos valores dependen de r y dado por x± ± =12r()r+1± ± ()r− − 3)()r+1)){displaystyle x_{pm }={frac {1}{2r}left(r+1pm {sqrt {(r-3)(r+1)}right)}.
• Con r entre 3.44949 y 3.54409 (aproximadamente), a partir de casi todas las condiciones iniciales, la población se acercará a oscilaciones permanentes entre cuatro valores. Este último número es una raíz de un polinomio de 12o grado (secuencia) A086181 en el OEIS).
• Con r aumentar más allá de 3.54409, desde casi todas las condiciones iniciales la población se aproximará a oscilaciones entre 8 valores, 16, 32, etc. Las longitudes de los intervalos de parámetro que producen oscilaciones de una longitud determinada disminuyen rápidamente; la relación entre las longitudes de dos intervalos de bifurcación sucesivos se acerca a la constante de Feigenbaum δ ■ 4.66920. Este comportamiento es un ejemplo de una cascada de doble duración.
• At r ■ 3.56995 (secuencia) A098587 en el OEIS) es el comienzo del caos, al final de la cascada de doble período. Desde casi todas las condiciones iniciales, ya no vemos oscilaciones de periodo finito. Las variaciones de la luz en la población inicial dan resultados dramáticamente diferentes con el tiempo, una característica primordial del caos.
• La mayoría de los valores r más allá de 3.56995 exhiben comportamiento caótico, pero todavía hay ciertos rangos aislados de r que muestran comportamiento no caótico; estos se llaman a veces islas de estabilidad. Por ejemplo, a partir de 1 +√8 (aproximadamente 3.8843) hay una gama de parámetros r que muestran oscilación entre tres valores, y para valores ligeramente superiores r oscilación entre 6 valores, luego 12 etc.
• El desarrollo del comportamiento caótico de la secuencia logística como parámetro r varía de aproximadamente 3.56995 a aproximadamente 3.82843 se llama a veces el escenario Pomeau-Manneville, caracterizado por una fase periódica (laminar) interrumpida por ráfagas de comportamiento aperiodico. Tal escenario tiene una aplicación en dispositivos semiconductores. Hay otros rangos que producen oscilación entre 5 valores, etc.; todos los períodos de oscilación ocurren para algunos valores de r. A ventana entre períodos con parámetro c es una gama de r-valores consistentes en una sucesión de subrangos. El kt subrange contiene los valores de r para el cual hay un ciclo estable (un ciclo que atrae un conjunto de puntos iniciales de medida unitaria) del período 2^kc. Esta secuencia de sub-ranges se llama a cascada de armónicos. En un subrango con un ciclo estable de período 2^k*c, hay ciclos inestables de período 2^kc para todos k. k*. El r valor al final de la secuencia infinita de sub-ranges se llama el punto de acumulación de la cascada de armónicos. As r surge una sucesión de ventanas nuevas con diferentes c valores. El primero es para c = 1; todas las ventanas posteriores que impliquen c se produce en orden decreciente c comenzando con arbitrariamente grande c.
• Más allá r = 4, casi todos los valores iniciales eventualmente salen del intervalo [0,1] y sumergir. El conjunto de condiciones iniciales que permanecen dentro [0,1] forma un conjunto Cantor y la dinámica restringida a este conjunto Cantor es caótica.

Para cualquier valor de r hay como máximo un ciclo estable. Si existe un ciclo estable, es globalmente estable, atrayendo casi todos los puntos. Algunos valores de r con un ciclo estable de algún período tienen infinitos ciclos inestables de varios períodos.

El diagrama de bifurcación de la derecha resume esto. El eje horizontal muestra los posibles valores del parámetro r mientras que el eje vertical muestra el conjunto de valores de x visitado asintóticamente desde casi todas las condiciones iniciales por las iteraciones de la ecuación logística con ese r valor.

Diagrama de Bifurcación para el mapa logístico. El atractivo para cualquier valor del parámetro r se muestra en la línea vertical en que r.

El diagrama de bifurcación es autosimilar: si nos acercamos al valor mencionado anteriormente r ≈ 3.82843 y nos enfocamos en un brazo de los tres, la situación cercana parece una versión reducida y ligeramente distorsionada de todo el diagrama. Lo mismo es cierto para todos los demás puntos no caóticos. Este es un ejemplo de la conexión profunda y omnipresente entre el caos y los fractales.

Magnificación de la región caótica del mapa.

Stable regions within the chaotic region, where a tangent bifurcation occurs at the boundary between the chaotic and periodic attractor, giving intermittent pathctories as described in the Pomeau-Manneville scenario.

También podemos considerar valores negativos de r:

• Para r entre -2 y -1 la secuencia logística también cuenta con comportamiento caótico.
• Con r entre -1 y 1 -√6 y para x₀ entre 1 y 1r y 1-1/r, la población se acercará a oscilaciones permanentes entre dos valores, como en el caso de r entre 3 y 1 +√6, y dado por la misma fórmula.

El caos y el mapa logístico

Un diagrama de cobweb del mapa logístico, mostrando comportamiento caótico para la mayoría de los valores r ■ 3.57

Función logística f (azul) y sus versiones iteradas f², f³, f⁴ y f⁵ para r = 3.5. Por ejemplo, para cualquier valor inicial en el eje horizontal, f⁴ da el valor del iterate cuatro iteraciones más tarde.

La relativa simplicidad del mapa logístico lo convierte en un punto de entrada ampliamente utilizado para considerar el concepto de caos. Una descripción aproximada del caos es que los sistemas caóticos exhiben una gran sensibilidad a las condiciones iniciales, una propiedad del mapa logístico para la mayoría de los valores de r entre aproximadamente 3,57 y 4 (como se indicó anteriormente). Una fuente común de tal sensibilidad a las condiciones iniciales es que el mapa representa un plegado y estiramiento repetido del espacio en el que se define. En el caso del mapa logístico, la ecuación de diferencia cuadrática que lo describe puede considerarse como una operación de estiramiento y plegado en el intervalo (0,1).

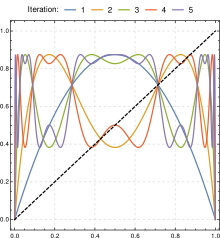
La siguiente figura ilustra cómo estirar y plegar una secuencia de iteraciones del mapa. La figura (a), a la izquierda, muestra un diagrama de Poincaré bidimensional del espacio de estado del mapa logístico para r = 4, y claramente muestra la curva cuadrática de la ecuación en diferencias (1). Sin embargo, podemos incrustar la misma secuencia en un espacio de estado tridimensional para investigar la estructura más profunda del mapa. La figura (b), a la derecha, demuestra esto, mostrando cómo los puntos inicialmente cercanos comienzan a divergir, particularmente en aquellas regiones de x_t correspondiente a las secciones más empinadas de la parcela.

Este estiramiento y plegado no solo produce una divergencia gradual de las secuencias de iteraciones, sino una divergencia exponencial (ver exponentes de Lyapunov), evidenciada también por la complejidad e imprevisibilidad del mapa logístico caótico. De hecho, la divergencia exponencial de secuencias de iteraciones explica la conexión entre el caos y la imprevisibilidad: un pequeño error en el supuesto estado inicial del sistema tenderá a corresponder a un gran error más adelante en su evolución. Por lo tanto, las predicciones sobre estados futuros se vuelven progresivamente (de hecho, exponencialmente) peores cuando hay incluso errores muy pequeños en nuestro conocimiento del estado inicial. Esta cualidad de imprevisibilidad y aparente aleatoriedad llevó a que la ecuación del mapa logístico se utilizara como un generador de números pseudoaleatorios en las primeras computadoras.

Dado que el mapa está confinado a un intervalo en la recta numérica real, su dimensión es menor o igual a la unidad. Las estimaciones numéricas arrojan una dimensión de correlación de 0.500±0,005 (Grassberger, 1983), una dimensión de Hausdorff de aproximadamente 0,538 (Grassberger 1981), y una dimensión de información de aproximadamente 0,5170976 (Grassberger 1983) para r ≈ 3.5699456 (inicio del caos). Nota: Se puede demostrar que la dimensión de correlación está ciertamente entre 0,4926 y 0,5024.

Sin embargo, a menudo es posible hacer afirmaciones precisas y exactas sobre la probabilidad de un estado futuro en un sistema caótico. Si un sistema dinámico (posiblemente caótico) tiene un atractor, entonces existe una medida de probabilidad que da la proporción a largo plazo del tiempo que pasa el sistema en las diversas regiones del atractor. En el caso del mapa logístico con parámetro r = 4 y un estado inicial en (0,1), el atractor es también el intervalo (0,1) y la medida de probabilidad corresponde a la distribución beta con parámetros a = 0,5 y b = 0,5. Específicamente, la medida invariante es

1π π x()1− − x).{displaystyle {frac {}}}}} {sqrt {x(1-x)}}}}}

La imprevisibilidad no es aleatoriedad, pero en algunas circunstancias se parece mucho a ella. Por lo tanto, y afortunadamente, incluso si sabemos muy poco sobre el estado inicial del mapa logístico (o algún otro sistema caótico), todavía podemos decir algo sobre la distribución de estados arbitrariamente lejanos en el futuro y usar este conocimiento para informar decisiones. según el estado del sistema.

Representación gráfica

El diagrama de bifurcación para el mapa logístico se puede visualizar con el siguiente código de Python:

importación numposo como npimportación matplotlib.pyplot como pltintervalo = ()2.8, 4) # start, endprecisión = 0,0001representantes = 600 # Número de repeticionesnumtoplot = 200lims = np.ceros()representantes)fig., biax = plt.subplots()fig..set_size_inches()16, 9)lims[0] = np.al azar.rand()para r dentro np.arange()intervalo[0] intervalo[1] precisión): para i dentro rango()representantes-1): lims[i+1] = r*lims[i]*()1-lims[i]) biax.parcela[r]*numtoplot, lims[representantes-numtoplot:] 'b. ', marcadores=.02)biax.set()xlabel='r ', Ylabel='x ', Título='Mapato logístico' ')plt.show()

Casos especiales del mapa

Límite superior cuando 0 ≤ r ≤ 1

Aunque las soluciones exactas para la relación de recurrencia solo están disponibles en un pequeño número de casos, se conoce un límite superior de forma cerrada en el mapa logístico cuando 0 ≤ r ≤ 1. Hay dos aspectos del comportamiento del mapa logístico que deben ser capturados por un límite superior en este régimen: el decaimiento geométrico asintótico con constante r, y el rápido decaimiento inicial cuando x₀ está cerca de 1, impulsado por (1 − x_n) término en la relación de recurrencia. El siguiente límite captura ambos efectos:

О О n▪ ▪ {}0,1,...... }yx0,r▪ ▪ [0,1],xn≤ ≤ x0r− − n+x0n.{displaystyle forall nin {0,1,ldots }quad {text{and}quad x_{0},rin [0,1],quad x_{n}leq {frac {x_{0} {r^{-n}+x_{0}} {0}} {cH0}} {cH0}} {cH0}}} {cH0}}}} {cH0}}} {cH0}} {cH0}}}}} {cH00}}}} {cH00}}}}}}}}}}}}}}} {cccccH00}}}}}}}}}} {ccccccccccH00}} {cccccccccccH00} {cH00}}}}}}}}}}}}}}} {cH00}}}}}}}}}}}}}}} {cccccccH00}}}}}}}}}}}}} {c

Solución cuando r = 4

El caso especial de r = 4 puede de hecho resolverse exactamente, al igual que el caso de r = 2; sin embargo, el caso general solo puede predecirse estadísticamente. La solución cuando r = 4 es,

xn=pecado2⁡ ⁡ ()2nSilencio Silencio π π ),{displaystyle x_{n}=sin ^{2}left(2^{n}theta piright),}

donde el parámetro de condición inicial θ viene dado por

Silencio Silencio =1π π pecado− − 1⁡ ⁡ ()x0).{displaystyle theta ={tfrac {1}{pi} }sin ^{-1}left({sqrt {x_{0}right).}

Para θ racionales, después de un número finito de iteraciones x_n se asigna a una secuencia periódica. Pero casi todos los θ son irracionales y, para los irracionales, θ, x_n nunca se repite, no es periódico. Esta ecuación de solución demuestra claramente las dos características clave del caos: estirarse y plegarse: el factor 2ⁿ muestra el crecimiento exponencial de estiramiento, lo que da como resultado una dependencia sensible de las condiciones iniciales, mientras que la función de seno al cuadrado mantiene x_n doblado dentro del rango [0,1].

Para r = 4 una solución equivalente en términos de números complejos en lugar de funciones trigonométricas es

xn=− − α α 2n− − α α − − 2n+24{displaystyle ¿Qué?.

donde α es cualquiera de los números complejos

α α =1− − 2x0± ± ()1− − 2x0)2− − 1{displaystyle alpha =1-2x_{0}pm {sqrt {left(1-2x_{0}right)^{2}-1}}

con módulo igual a 1. Así como la función de seno al cuadrado en la solución trigonométrica no conduce ni a la contracción ni a la expansión del conjunto de puntos visitados, en la última solución este efecto se logra mediante el módulo unitario de α.

Por el contrario, la solución cuando r = 2 es

xn=12− − 12()1− − 2x0)2n{displaystyle x_{n}={tfrac {1}{2}-{tfrac {1}{2}left(1-2x_{0}right)}{2^{n}}

para x₀ ∈ [0,1). Dado que (1 − 2x₀) ∈ (−1,1) para cualquier valor de x₀ que no sea el punto fijo inestable 0, el término (1 − 2x₀)²ⁿ va a 0 como n va hasta el infinito, entonces x_n va al punto fijo estable 1/2.

Encontrar ciclos de cualquier longitud cuando r = 4

Para el caso r = 4, desde casi todas las condiciones iniciales, la secuencia de iteración es caótica. Sin embargo, existe un número infinito de condiciones iniciales que dan lugar a ciclos, y de hecho existen ciclos de longitud k para todos enteros k > 0. Podemos explotar la relación del mapa logístico con la transformación diádica (también conocida como mapa de desplazamiento de bits) para encontrar ciclos de cualquier longitud. Si x sigue el mapa logístico x_{n + 1} = 4x_n(1 − x_n) y y sigue la transformación diádica

<math alttext="{displaystyle y_{n+1}={begin{cases}2y_{n}&0leq y_{n}<{tfrac {1}{2}}\2y_{n}-1&{tfrac {1}{2}}leq y_{n}Sí.n+1={}2Sí.n0≤ ≤ Sí.n.122Sí.n− − 112≤ ≤ Sí.n.1,{displaystyle Y_{n+1}={begin{cases}2y_{n} Y... {1}{2}2y_{n}-1 {1} {2}leq y_{n}Se hizo1,end{cases}}<img alt="{displaystyle y_{n+1}={begin{cases}2y_{n}&0leq y_{n}<{tfrac {1}{2}}\2y_{n}-1&{tfrac {1}{2}}leq y_{n}

entonces los dos están relacionados por un homeomorfismo

xn=pecado2⁡ ⁡ ()2π π Sí.n).{displaystyle x_{n}=sin ^{2}left(2pi y_{n}right).}

La razón por la que la transformación dyadica también se llama el mapa de bit-shift es que cuando Sí. está escrito en notación binaria, el mapa mueve el punto binario un lugar a la derecha (y si el bit a la izquierda del punto binario se ha convertido en un "1", este "1" se cambia a un "0"). Un ciclo de longitud 3, por ejemplo, ocurre si un itinerario tiene una secuencia de repetición de 3 bits en su expansión binaria (que no es también una secuencia de repetición de un solo bit): 001, 010, 100, 110, 101, o 011. El itinerario 001001001... mapas en 010010010..., que mapas en 100100100..., que a su vez mapas en el original 001001001...; así que este es un 3 ciclo del mapa de bits. Y las otras tres secuencias de repetición de expansión binaria dan el 3 ciclo 110110... → 101101... → 011011011... → 110110.... Cualquiera de estos 3 ciclos se puede convertir en forma fraccionada: por ejemplo, el primer ciclo dado puede ser escrito como 1/7 → 2/7 → 4/7 → 1/7. Utilizando la traducción anterior del mapa bit-shift al mapa r=4{displaystyle r=4} mapa logístico da el ciclo logístico correspondiente 0.611260467... → 0.950484434... → 0.188255099... → 0.611260467.... También podríamos traducir el otro bit-shift 3-cycle en su correspondiente ciclo logístico. Del mismo modo, ciclos de cualquier longitud k se puede encontrar en el mapa de bit-shift y luego se traduce en los ciclos logísticos correspondientes.

Sin embargo, dado que casi todos los números en [0,1) son irracionales, casi todas las condiciones iniciales del mapa de desplazamiento de bits conducen a la no periodicidad del caos. Esta es una forma de ver que el mapa logístico r = 4 es caótico para casi todas las condiciones iniciales.

El número de ciclos de longitud (mínima) k = 1, 2, 3,… para el mapa logístico con r = 4 (mapa de tienda con μ = 2) es una secuencia entera conocida (secuencia A001037 en el OEIS): 2, 1, 2, 3, 6, 9, 18, 30, 56, 99, 186, 335, 630, 1161... Esto nos dice que el mapa logístico con r = 4 tiene 2 puntos fijos, 1 ciclo de longitud 2, 2 ciclos de longitud 3 y así sucesivamente. Esta secuencia toma una forma particularmente simple para números primos k: 2 ⋅ 2^{k − 1} − 1 //span>k. Por ejemplo: 2 ⋅ 2^{13 − 1} − 1/13 = 630 es el número de ciclos de longitud 13. Dado que este caso del mapa logístico es caótico para casi todos los condiciones, todos estos ciclos de longitud finita son inestables.

Conceptos relacionados

Universalidad de Feigenbaum de mapas 1-D

Universalidad de mapas unidimensionales con maxima parabólica y constantes Feigenbaum δ δ =4.669201...{displaystyle delta =4.669201...}, α α =2.502907...{displaystyle alpha =2.502907...} es bien visible con el mapa propuesto como un juguete modelo para dinámicas láser discretas: x→ → Gx()1− − Tanh⁡ ⁡ ()x)){displaystyle xrightarrow Gx(1-tanh(x)}, Donde x{displaystyle x} representa la amplitud del campo eléctrico, G{displaystyle G. es ganancia láser como parámetro de bifurcación.

El aumento gradual G{displaystyle G. a intervalos [0,JUEGO JUEGO ){displaystyle [0,infty]} cambia dinámicas de regular a caótica con cualitativamente el mismo diagrama de bifurcación que los de mapa logístico.