Mapa lineal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función matemática, en álgebra lineal

En matemáticas, y más específicamente en álgebra lineal, a mapa lineal (también llamado a cartografía lineal, transformación lineal, homomorfismo espacial vectorial, o en algunos contextos función lineal) es un mapeo $Vto W$ entre dos espacios vectoriales que preserva las operaciones de la adición vectorial y la multiplicación del escalar. Los mismos nombres y la misma definición también se utilizan para el caso más general de módulos sobre un anillo; véase el homomorfismo del módulo.

Si un mapa lineal es una bijeción entonces se llama isomorfismo lineal. En el caso en que ${displaystyle V=W}$ , un mapa lineal se llama a (linear) endomorfismo. A veces el término operador lineal se refiere a este caso, pero el término "operador lineal" puede tener diferentes significados para diferentes convenciones: por ejemplo, se puede utilizar para enfatizar que $V$ y $W$ son espacios vectoriales reales (no necesariamente con ${displaystyle V=W}$ ), o se puede utilizar para enfatizar que $V$ es un espacio de función, que es una convención común en el análisis funcional. A veces el término función lineal tiene el mismo significado que mapa lineal, mientras que en análisis no lo hace.

Un mapa lineal de V a W siempre mapea el origen de V al origen de W. Además, asigna subespacios lineales en V a subespacios lineales en W (posiblemente de una dimensión inferior); por ejemplo, asigna un plano a través del origen en V a un plano a través del origen en W, una línea a través del origen en W, o simplemente el origen en W. Los mapas lineales a menudo se pueden representar como matrices, y los ejemplos simples incluyen transformaciones lineales de rotación y reflexión.

En el lenguaje de la teoría de categorías, los mapas lineales son los morfismos de los espacios vectoriales.

Definición y primeras consecuencias

Vamos $V$ y $W$ ser espacios vectoriales sobre el mismo campo $K$ . Una función $f:Vto W$ se dice que es un mapa lineal si para cualquier dos vectores ${textstyle mathbf {u}mathbf {v} in V}$ y cualquier escalar ${displaystyle cin K}$ las dos condiciones siguientes están satisfechas:

Aditividad / operación de adición ${displaystyle f(mathbf {u} +mathbf {v})=f(mathbf {u})+f(mathbf {v})}$
Homogeneidad del grado 1 / operación de multiplicación de escalar ${displaystyle f(cmathbf {u})=cf(mathbf {u})}$

Por lo tanto, se dice que un mapa lineal preserva la operación. En otras palabras, no importa si el mapa lineal se aplica antes (los lados derechos de los ejemplos anteriores) o después (los lados izquierdos de los ejemplos) de las operaciones de suma y multiplicación escalar.

Por la asociación de la operación de adición denotó como +, para cualquier vector ${textstyle mathbf {u} _{1},ldotsmathbf {u} _{n}in V}$ and scalars ${textstyle c_{1},ldotsc_{n}in K,}$ la siguiente igualdad establece:

{displaystyle f(c_{1}mathbf {u} _{1}+cdots +c_{n}mathbf {u} _{n})=c_{1}f(mathbf {u} _{1})+cdots +c_{n}f(mathbf {u} _{n}).}

Denotar los elementos cero de los espacios vectoriales $V$ y $W$ por ${textstyle mathbf {0} _{V}}$ y ${textstyle mathbf {0} _{W}}$ respectivamente, sigue que ${textstyle f(mathbf {0} _{V})=mathbf {0} _{W}.}$ Vamos $c=0$ y ${textstyle mathbf {v} in V}$ en la ecuación para la homogeneidad del grado 1:

{displaystyle f(mathbf {0} _{V})=f(0mathbf {v})=0f(mathbf {v})=mathbf {0} _{W}.}

Un mapa lineal ${displaystyle Vto K}$ con $K$ visto como un espacio vectorial único sobre sí mismo se llama un funcional lineal.

Estas declaraciones se generalizan a cualquier módulo izquierdo ${textstyle {}_{R}M}$ sobre un anillo $R$ sin modificación, y a cualquier modelo adecuado al invertir la multiplicación del escalar.

Ejemplos

Un ejemplo prototípico que da mapas lineales su nombre es una función ${displaystyle f:mathbb {R} to mathbb {R}:xmapsto cx}$ , del cual el gráfico es una línea a través del origen.
Más generalmente, cualquier homothety ${textstyle mathbf {v} mapsto cmathbf {v} }$ Donde $c$ centrado en el origen de un espacio vectorial es un mapa lineal.
El mapa cero ${textstyle mathbf {x} mapsto mathbf {0} }$ entre dos espacios vectoriales (sobre el mismo campo) es lineal.
El mapa de identidad en cualquier módulo es un operador lineal.
Para números reales, el mapa ${textstyle xmapsto x^{2}}$ no es lineal.
Para números reales, el mapa ${textstyle xmapsto x+1}$ no es lineal (pero es una transformación afinada).
Si $A$ es un $mtimes n$ matriz real, entonces $A$ define un mapa lineal desde $mathbb {R} ^{n}$ a $mathbb{R} ^{m}$ por enviar un vector de columna ${displaystyle mathbf {x} in mathbb {R} ^{n}}$ al vector de la columna ${displaystyle Amathbf {x} in mathbb {R} ^{m}}$ . Por el contrario, cualquier mapa lineal entre espacios vectoriales finitos-dimensionales puede ser representado de esta manera; vea el § Matrices, abajo.
Si ${textstyle f:Vto W}$ es una isometría entre los verdaderos espacios nórdicos tal que ${textstyle f(0)=0}$ entonces $f$ es un mapa lineal. Este resultado no es necesariamente cierto para el espacio complejo y ordenado.
Diferenciación define un mapa lineal desde el espacio de todas las funciones diferenciables hasta el espacio de todas las funciones. También define un operador lineal en el espacio de todas las funciones suaves (un operador lineal es lineal endomorfismo, es decir, un mapa lineal con el mismo dominio y codomain). Un ejemplo es ${displaystyle {frac {d}{dx}}left(c_{1}f_{1}(x)+c_{2}f_{2}(x)+cdots +c_{n}f_{n}(x)right)=c_{1}{frac {df_{1}(x)}{dx}}+c_{2}{frac {df_{2}(x)}{dx}}+cdots +c_{n}{frac {df_{n}(x)}{dx}}.}$
Una integral definida en algún intervalo $I$ es un mapa lineal desde el espacio de todas las funciones integrables de valor real en $I$ a $mathbb {R}$ . Por ejemplo, ${displaystyle int _{a}^{b}left[c_{1}f_{1}(x)+c_{2}f_{2}(x)+dots +c_{n}f_{n}(x)right],dx={c_{1}int _{a}^{b}f_{1}(x),dx}+c_{2}int _{a}^{b}f_{2}(x),dx+cdots +c_{n}int _{a}^{b}f_{n}(x),dx.}$
Una integral indefinida (o antiderivativa) con un punto de partida de integración fijo define un mapa lineal desde el espacio de todas las funciones integradoras de valor real en $mathbb {R}$ al espacio de todas las funciones de valor real y diferenciables en $mathbb {R}$ . Sin un punto de partida fijo, los mapas antiderivativos al espacio cociente de las funciones diferenciables por el espacio lineal de funciones constantes.
Si $V$ y $W$ son espacios vectoriales de dimensión finita sobre un campo $F$ , de las dimensiones respectivas $m$ y $n$ , entonces la función que mapea mapas lineales ${textstyle f:Vto W}$ a $n \times m$ matrices en la forma descrita en § Matrices (bajo) es un mapa lineal, e incluso un isomorfismo lineal.
El valor esperado de una variable aleatoria (que es de hecho una función, y como tal elemento de un espacio vectorial) es lineal, como para variables aleatorias $X$ y $Y$ tenemos ${displaystyle E[X+Y]=E[X]+E[Y]}$ y ${displaystyle E[aX]=aE[X]}$ , pero la variabilidad de una variable aleatoria no es lineal.

La función ${textstyle f:mathbb {R} ^{2}to mathbb {R} ^{2}}$ con ${textstyle f(x,y)=(2x,y)}$ es un mapa lineal. Esta función escala los ${textstyle x}$ componente de un vector por el factor ${textstyle 2}$ .
La función ${textstyle f(x,y)=(2x,y)}$ es aditivo: No importa si los vectores se añaden primero y luego se mapean o si se mapean y finalmente se añaden: ${textstyle f(mathbf {a} +mathbf {b})=f(mathbf {a})+f(mathbf {b})}$
La función ${textstyle f(x,y)=(2x,y)}$ es homogénea: No importa si un vector es escalado primero y luego mapeado o mapeado por primera vez y luego escalado: ${textstyle f(lambda mathbf {a})=lambda f(mathbf {a})}$

Extensiones lineales

A menudo, un mapa lineal se construye definiéndolo en un subconjunto de un espacio vectorial y luego extendiéndolo por linearidad al lazo lineal del dominio. A extensión lineal de una función $f$ es una extensión de $f$ a un espacio vectorial que es un mapa lineal.

Suppose $X$ y $Y$ son espacios vectoriales y ${displaystyle f:Sto Y}$ es una función definida en algún subconjunto ${displaystyle Ssubseteq X.}$ Entonces... $f$ se puede ampliar a un mapa lineal ${displaystyle F:operatorname {span} Sto Y}$ si $0}" xmlns="http://www.w3.org/1998/Math/MathML">n■0{displaystyle n confiado0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27a6a5d982d54202a14f111cb8a49210501b2c96" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ es un entero, $c_{1},ldotsc_{n}$ son escalares, y ${displaystyle s_{1},ldotss_{n}in S}$ son vectores tales que ${displaystyle 0=c_{1}s_{1}+cdots +c_{n}s_{n},}$ entonces necesariamente ${displaystyle 0=c_{1}fleft(s_{1}right)+cdots +c_{n}fleft(s_{n}right).}$ Si una extensión lineal ${displaystyle f:Sto Y}$ existe entonces la extensión lineal ${displaystyle F:operatorname {span} Sto Y}$ es único y

{displaystyle Fleft(c_{1}s_{1}+cdots c_{n}s_{n}right)=c_{1}fleft(s_{1}right)+cdots +c_{n}fleft(s_{n}right)}

{displaystyle n,c_{1},ldotsc_{n},}

{displaystyle s_{1},ldotss_{n}}

S

{displaystyle f:Sto Y}

{displaystyle ;operatorname {span} Sto Y}

Por ejemplo, si ${displaystyle X=mathbb {R} ^{2}}$ y ${displaystyle Y=mathbb {R} }$ entonces la asignación ${displaystyle (1,0)to -1}$ y ${displaystyle (0,1)to 2}$ se puede ampliar linealmente del conjunto linealmente independiente de vectores ${displaystyle S:={(1,0),(0,1)}}$ a un mapa lineal en ${displaystyle operatorname {span} {(1,0),(0,1)}=mathbb {R} ^{2}.}$ La extensión lineal única ${displaystyle F:mathbb {R} ^{2}to mathbb {R} }$ es el mapa que envía ${displaystyle (x,y)=x(1,0)+y(0,1)in mathbb {R} ^{2}}$ a

{displaystyle F(x,y)=x(-1)+y(2)=-x+2y.}

Cada (valorado escalar) funcionamiento lineal $f$ definido en un subespacio vectorial de un espacio vectorial real o complejo $X$ tiene una extensión lineal a todos $X.$ De hecho, el teorema de extensión dominado Hahn-Banach garantiza incluso que cuando este funcional lineal $f$ está dominado por algunos seminorm dado ${displaystyle p:Xto mathbb {R} }$ (que significa que ${displaystyle |f(m)|leq p(m)}$ para todos $m$ en el dominio de $f$ ) entonces existe una extensión lineal $X$ que también está dominado $p.$

Matrices

Si $V$ y $W$ son espacios vectoriales finitos y una base se define para cada espacio vectorial, entonces cada mapa lineal de $V$ a $W$ puede ser representado por una matriz. Esto es útil porque permite cálculos concretos. Las matrices dan ejemplos de mapas lineales: si $A$ es un verdadero $mtimes n$ matriz, entonces ${displaystyle f(mathbf {x})=Amathbf {x} }$ describe un mapa lineal ${displaystyle mathbb {R} ^{n}to mathbb {R} ^{m}}$ (ver Espacio Euclideano).

Vamos ${displaystyle {mathbf {v} _{1},ldotsmathbf {v} _{n}}}$ ser una base para $V$ . Entonces cada vector ${displaystyle mathbf {v} in V}$ está determinado por los coeficientes ${displaystyle c_{1},ldotsc_{n}}$ sobre el terreno $mathbb {R}$ :

{displaystyle mathbf {v} =c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n}.}

Si ${textstyle f:Vto W}$ es un mapa lineal,

{displaystyle f(mathbf {v})=f(c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n})=c_{1}f(mathbf {v} _{1})+cdots +c_{n}fleft(mathbf {v} _{n}right),}

que implica la función f es enteramente determinado por los vectores ${displaystyle f(mathbf {v} _{1}),ldotsf(mathbf {v} _{n})}$ . Ahora ${displaystyle {mathbf {w} _{1},ldotsmathbf {w} _{m}}}$ ser una base para $W$ . Entonces podemos representar cada vector ${displaystyle f(mathbf {v} _{j})}$ como

{displaystyle fleft(mathbf {v} _{j}right)=a_{1j}mathbf {w} _{1}+cdots +a_{mj}mathbf {w} _{m}.}

Así, la función $f$ está completamente determinado por los valores de $a_{ij}$ . Si ponemos estos valores en un $mtimes n$ matriz $M$ , entonces podemos utilizarlo convenientemente para calcular la salida vectorial $f$ para cualquier vector en $V$ . Para conseguir $M$ , cada columna $j$ de $M$ es un vector

{displaystyle {begin{pmatrix}a_{1j}\vdots \a_{mj}end{pmatrix}}}

{displaystyle f(mathbf {v} _{j})}

j

{displaystyle f(mathbf {v} _{j})}

{displaystyle mathbf {M} ={begin{pmatrix} cdots &a_{1j}&cdots \&vdots &\&a_{mj}&end{pmatrix}}}

M

f

j=1,ldotsn

{displaystyle f(mathbf {v} _{j})}

{displaystyle a_{1j},cdotsa_{mj}}

j

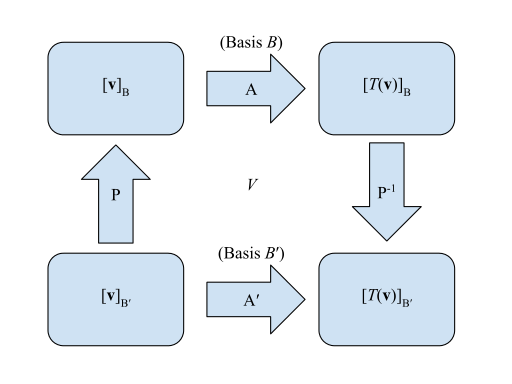
Las matrices de una transformación lineal se pueden representar visualmente:

Matriz para ${textstyle T}$ relativa a ${textstyle B}$ : ${textstyle A}$
Matriz para ${textstyle T}$ relativa a ${textstyle B'}$ : ${textstyle A'}$
Matriz de transición ${textstyle B'}$ a ${textstyle B}$ : ${textstyle P}$
Matriz de transición ${textstyle B}$ a ${textstyle B'}$ : ${textstyle P^{-1}}$

La relación entre matrices en una transformación lineal

Tal que comienza en la esquina inferior izquierda ${textstyle left[mathbf {v} right]_{B'}}$ y buscando la esquina inferior derecha ${textstyle left[Tleft(mathbf {v} right)right]_{B'}}$ , uno se dejaría-multiplicadamente - es decir, ${textstyle A'left[mathbf {v} right]_{B'}=left[Tleft(mathbf {v} right)right]_{B'}}$ . El método equivalente sería el método "peligro" que va en sentido de reloj desde el mismo punto tal que ${textstyle left[mathbf {v} right]_{B'}}$ está multiplicado por la izquierda ${textstyle P^{-1}AP}$ , o ${textstyle P^{-1}APleft[mathbf {v} right]_{B'}=left[Tleft(mathbf {v} right)right]_{B'}}$ .

Ejemplos en dos dimensiones

En el espacio bidimensional R² los mapas lineales se describen mediante matrices de 2 × 2. Estos son algunos ejemplos:

rotación
- por 90 grados a la derecha: ${displaystyle mathbf {A} ={begin{pmatrix}0&-1\1&0end{pmatrix}}}$
- por un ángulo Silencio en sentido contrario: ${displaystyle mathbf {A} ={begin{pmatrix}cos theta &-sin theta \sin theta &cos theta end{pmatrix}}}$
reflexión
- a través de x axis: ${displaystyle mathbf {A} ={begin{pmatrix}1&0\0&-1end{pmatrix}}}$
- a través de Sí. axis: ${displaystyle mathbf {A} ={begin{pmatrix}-1&0\0&1end{pmatrix}}}$
- a través de una línea haciendo un ángulo Silencio con el origen: ${displaystyle mathbf {A} ={begin{pmatrix}cos 2theta &sin 2theta \sin 2theta &-cos 2theta end{pmatrix}}}$
escalando por 2 en todas direcciones: ${displaystyle mathbf {A} ={begin{pmatrix}2&0\0&2end{pmatrix}}=2mathbf {I} }$
cartografía horizontal: ${displaystyle mathbf {A} ={begin{pmatrix}1&m\0&1end{pmatrix}}}$
mapeo de presión: ${displaystyle mathbf {A} ={begin{pmatrix}k&0\0&{frac {1}{k}}end{pmatrix}}}$
proyección sobre la Sí. axis: ${displaystyle mathbf {A} ={begin{pmatrix}0&0\0&1end{pmatrix}}.}$

Espacio vectorial de mapas lineales

La composición de los mapas lineales es lineal: si $f:Vto W$ y ${textstyle g:Wto Z}$ son lineales, entonces también su composición ${textstyle gcirc f:Vto Z}$ . De esto se desprende que la clase de todos los espacios vectoriales sobre un campo dado K, junto con K- mapas lineales como morfismos, forma una categoría.

El inverso de un mapa lineal, cuando se define, es nuevamente un mapa lineal.

Si ${textstyle f_{1}:Vto W}$ y ${textstyle f_{2}:Vto W}$ son lineales, entonces así es su suma de sentido $f_1 + f_2$ , que se define por ${displaystyle (f_{1}+f_{2})(mathbf {x})=f_{1}(mathbf {x})+f_{2}(mathbf {x})}$ .

Si ${textstyle f:Vto W}$ es lineal y ${textstyle alpha }$ es un elemento del campo terrestre ${textstyle K}$ , entonces el mapa ${textstyle alpha f}$ , definida por ${textstyle (alpha f)(mathbf {x})=alpha (f(mathbf {x}))}$ , también es lineal.

Así el conjunto ${textstyle {mathcal {L}}(V,W)}$ de mapas lineales de ${textstyle V}$ a ${textstyle W}$ forma un espacio vectorial sobre ${textstyle K}$ , a veces denotado ${textstyle operatorname {Hom} (V,W)}$ . Además, en el caso de que ${textstyle V=W}$ , este espacio vectorial, denotado ${textstyle operatorname {End} (V)}$ , es un álgebra asociativa bajo composición de mapas, ya que la composición de dos mapas lineales es de nuevo un mapa lineal, y la composición de mapas es siempre asociativa. Este caso se examina con más detalle a continuación.

Dado nuevamente el caso de dimensión finita, si se han elegido bases, entonces la composición de mapas lineales corresponde a la multiplicación de matrices, la suma de mapas lineales corresponde a la suma de matrices y la multiplicación de mapas lineales con escalares corresponde a la multiplicación de matrices con escalares.

Endomorfismos y automorfismos

Una transformación lineal ${textstyle f:Vto V}$ es un endomorfismo ${textstyle V}$ ; el conjunto de todos estos endomorfismos ${textstyle operatorname {End} (V)}$ junto con la adición, composición y multiplicación de escalar tal como se define arriba formas un álgebra asociativa con elemento de identidad sobre el campo ${textstyle K}$ (y en particular un anillo). El elemento de identidad multiplicativo de este álgebra es el mapa de identidad ${textstyle operatorname {id}:Vto V}$ .

Un endomorfismo ${textstyle V}$ que es también un isomorfismo se llama automorfismo ${textstyle V}$ . La composición de dos automorfismos es otra vez un automorfismo, y el conjunto de todos los automorfismos ${textstyle V}$ forma un grupo, el grupo de automorfismo ${textstyle V}$ que se denota ${textstyle operatorname {Aut} (V)}$ o ${textstyle operatorname {GL} (V)}$ . Puesto que los automorfismos son precisamente aquellos endomorfismos que poseen inversos bajo composición, ${textstyle operatorname {Aut} (V)}$ es el grupo de unidades en el anillo ${textstyle operatorname {End} (V)}$ .

Si ${textstyle V}$ tiene dimensión finita ${textstyle n}$ , entonces ${textstyle operatorname {End} (V)}$ es isomorfo al álgebra asociativa de todos ${textstyle ntimes n}$ matrices con entradas ${textstyle K}$ . El grupo de automorfismo ${textstyle V}$ es isomorfa al grupo lineal general ${textstyle operatorname {GL} (n,K)}$ de todos ${textstyle ntimes n}$ matrices invertibles con entradas ${textstyle K}$ .

Kernel, imagen y el teorema de rango-nulidad

Si ${textstyle f:Vto W}$ es lineal, definimos el núcleo y la imagen o rango de ${textstyle f}$ por

{displaystyle {begin{aligned}ker(f)&={,mathbf {x} in V:f(mathbf {x})=mathbf {0} ,}\operatorname {im} (f)&={,mathbf {w} in W:mathbf {w} =f(mathbf {x}),mathbf {x} in V,}end{aligned}}}

${textstyle ker(f)}$ es un subespacio ${textstyle V}$ y ${textstyle operatorname {im} (f)}$ es un subespacio ${textstyle W}$ . La siguiente fórmula de dimensión se conoce como el teorema de rango anual:

{displaystyle dim(ker(f))+dim(operatorname {im} (f))=dim(V).}

El número ${textstyle dim(operatorname {im} (f))}$ también se llama el rango de ${textstyle f}$ y escrito como ${textstyle operatorname {rank} (f)}$ , o a veces, ${textstyle rho (f)}$ ; el número ${textstyle dim(ker(f))}$ se llama la nulidad de ${textstyle f}$ y escrito como ${textstyle operatorname {null} (f)}$ o ${textstyle nu (f)}$ . Si ${textstyle V}$ y ${textstyle W}$ son finitos-dimensionales, bases han sido elegidas y ${textstyle f}$ está representado por la matriz ${textstyle A}$ , entonces el rango y la nulidad de ${textstyle f}$ son iguales al rango y la nulidad de la matriz ${textstyle A}$ , respectivamente.

Cokernel

Un invariante más sutil de una transformación lineal ${textstyle f:Vto W}$ es el cokernel, que se define como

{displaystyle operatorname {coker} (f):=W/f(V)=W/operatorname {im} (f).}

Esta es la noción dual del núcleo: así como el núcleo es un subespacio del dominio, el co-núcleo es un espacio cociente del objetivo. Formalmente, uno tiene la secuencia exacta

{displaystyle 0to ker(f)to Vto Wto operatorname {coker} (f)to 0.}

Estos pueden interpretarse así: dada una ecuación lineal f(v) = w para resolver,

el núcleo es el espacio de soluciones a la homogénea ecuación f()v) = 0, y su dimensión es el número de grados de libertad en el espacio de las soluciones, si no está vacía;
el co-kernel es el espacio de limitaciones que las soluciones deben satisfacer, y su dimensión es el número máximo de limitaciones independientes.

La dimensión del co-kernel y la dimensión de la imagen (el rango) suman la dimensión del espacio de destino. Para dimensiones finitas, esto significa que la dimensión del espacio cociente W/f(V) es la dimensión del espacio objetivo menos la dimensión de la imagen

Como ejemplo simple, considere el mapa f: R² → R², dado por f()x, Sí.) = (0, Sí.). Entonces para una ecuación f()x, Sí.) =a, b) para tener una solución, debemos tener a = 0 (una limitación), y en ese caso el espacio de solución es (x, b) o equivalentemente declarado, (0, b) + (x, 0), (un grado de libertad). El núcleo puede ser expresado como el subespacio (x, 0) V: el valor de x es la libertad en una solución – mientras que el cokernel puede ser expresado a través del mapa W → R, ${textstyle (a,b)mapsto (a)}$ : dado un vectora, b), el valor de a es obstrucción para que haya una solución.

Un ejemplo ilustrando el caso infinite-dimensional es proporcionado por el mapa f: R^JUEGO → R^JUEGO, ${textstyle left{a_{n}right}mapsto left{b_{n}right}}$ con b₁ = 0 y b_{n + 1} = a_n para n ■ 0. Su imagen consiste en todas las secuencias con el primer elemento 0, y por lo tanto su cokernel consiste en las clases de secuencias con el primer elemento idéntico. Así, mientras que su núcleo tiene dimensión 0 (sólo mapea la secuencia cero a la secuencia cero), su co-carne tiene dimensión 1. Puesto que el dominio y el espacio objetivo son iguales, el rango y la dimensión del núcleo agregan a la misma suma que el rango y la dimensión del co-kernel ( ${textstyle aleph _{0}+0=aleph _{0}+1}$ ), pero en el caso infinita-dimensional no se puede inferir que el núcleo y el co-carne de un endomorfismo tienen la misma dimensión (0 ≠1). La situación inversa obtiene para el mapa h: R^JUEGO → R^JUEGO, ${textstyle left{a_{n}right}mapsto left{c_{n}right}}$ con c_n = a_{n + 1}. Su imagen es todo el espacio objetivo, y por lo tanto su co-quenel tiene dimensión 0, pero ya que mapea todas las secuencias en las que sólo el primer elemento no es cero a la secuencia cero, su núcleo tiene dimensión 1.

Índice

Para un operador lineal con núcleo y co-núcleo de dimensión finita, uno puede definir índice como:

{displaystyle operatorname {ind} (f):=dim(ker(f))-dim(operatorname {coker} (f)),}

Para una transformación entre espacios vectoriales de dimensión finita, esta es solo la diferencia dim(V) − dim(W), por rango-nulidad. Esto da una indicación de cuántas soluciones o cuántas restricciones tiene uno: si se mapea de un espacio más grande a uno más pequeño, el mapa puede estar sobre y, por lo tanto, tendrá grados de libertad incluso sin restricciones. Por el contrario, si se mapea de un espacio más pequeño a uno más grande, el mapa no puede ser sobre y, por lo tanto, uno tendrá restricciones incluso sin grados de libertad.

El índice de un operador es precisamente la característica de Euler del complejo de 2 términos 0 → V → W → 0. En la teoría de operadores, el índice de los operadores de Fredholm es un objeto de estudio, siendo un resultado importante el teorema del índice de Atiyah-Singer.

Clasificaciones algebraicas de transformaciones lineales

Ninguna clasificación de mapas lineales podría ser exhaustiva. La siguiente lista incompleta enumera algunas clasificaciones importantes que no requieren ninguna estructura adicional en el espacio vectorial.

Sea $V$ y $W$ denota espacios vectoriales sobre un campo $F$ y deja $T : V \to W$ sea un mapa lineal.

Monomorfismo

$T$ se dice que es inyectivo o un monomorfismo si cualquiera de las siguientes condiciones equivalentes es verdadera:

$T$ es uno a uno como un mapa de conjuntos.
$ker T = {0} V}$
$dim(ker) T) = 0$
$T$ es monic o de izquierda-cancelable, que es decir, para cualquier espacio vectorial $U$ y cualquier par de mapas lineales $R : U \to V$ y $S : U \to V$ , la ecuación $TR = TS$ implicación $R = S$ .
$T$ es invertible izquierda, que es decir que existe un mapa lineal $S : W \to V$ tales que $ST$ es el mapa de identidad en $V$ .

Epimorfismo

$T$ se dice que es sobreyectiva o un epimorfismo si cualquiera de las siguientes condiciones equivalentes es verdadera:

$T$ está en un mapa de conjuntos.
$coker T = {0} W}$
$T$ es épico o bien-cancelable, que es decir, para cualquier espacio vectorial $U$ y cualquier par de mapas lineales $R : W \to U$ y $S : W \to U$ , la ecuación $RT = ST$ implicación $R = S$ .
$T$ es derecho-invertible, que es decir que existe un mapa lineal $S : W \to V$ tales que $TS$ es el mapa de identidad en $W$ .

Isomorfismo

$T$ se dice que es un isomorfismo si es invertible a la izquierda y a la derecha. Esto es equivalente a que $T$ sea uno a uno y sobre (una biyección de conjuntos) o también a $T$ siendo tanto épico como mónico, por lo que es un bimorfismo.

Si $T : V \to V$ es un endomorfismo, entonces:

Si, por algún entero positivo $n$ , el $n$ - el itinerario $T$ , $T n$ , es idéntico cero, entonces $T$ se dice que es nilpotente.
Si $T 2 = T$ , entonces $T$ se dice que es idempotente
Si $T = kI$ , donde $k$ es un escalar, entonces $T$ se dice que es un mapa de transformación de escalar o multiplicación de escalar; vea la matriz de escalar.

Cambio de base

Dado un mapa lineal que es un endomorfismo cuya matriz es A, en la base B del espacio transforma las coordenadas vectoriales [u] como [v] = A[u]. Como los vectores cambian con el inverso de B (los vectores son contravariantes) su transformación inversa es [v] = B[v'].

Sustituyendo esto en la primera expresión

{displaystyle Bleft[v'right]=ABleft[u'right]}

{displaystyle left[v'right]=B^{-1}ABleft[u'right]=A'left[u'right].}

Por lo tanto, la matriz en la nueva base es A′ = B⁻¹AB, siendo B la matriz de la base dada.

Por lo tanto, se dice que los mapas lineales son objetos 1-co- 1-contra-variante, o tensores de tipo (1, 1).

Continuidad

Una transformación lineal entre espacios vectoriales topológicos, por ejemplo espacios normados, puede ser continua. Si su dominio y codominio son iguales, entonces será un operador lineal continuo. Un operador lineal en un espacio lineal normado es continuo si y solo si está acotado, por ejemplo, cuando el dominio es de dimensión finita. Un dominio de dimensión infinita puede tener operadores lineales discontinuos.

Un ejemplo de una transformación lineal ilimitada, por lo tanto discontinua, es la diferenciación en el espacio de funciones suaves equipadas con la norma suprema (una función con valores pequeños puede tener una derivada con valores grandes, mientras que la derivada de 0 es 0). Para un ejemplo específico, $sin(nx)/ n$ converge a 0, pero su derivado $cos(nx)$ no lo hace, por lo que la diferenciación no es continua en 0 (y por una variación de este argumento, no es continua en ninguna parte).

Aplicaciones

Una aplicación específica de los mapas lineales es para transformaciones geométricas, como las realizadas en gráficos por computadora, donde la traslación, rotación y escalado de objetos 2D o 3D se realiza mediante el uso de una matriz de transformación. Las asignaciones lineales también se utilizan como mecanismo para describir el cambio: por ejemplo, en cálculo corresponden a derivadas; o en relatividad, utilizado como un dispositivo para realizar un seguimiento de las transformaciones locales de los marcos de referencia.

Otra aplicación de estas transformaciones es la optimización del compilador de código de bucle anidado y la paralelización de técnicas de compilación.

Contenido relacionado

Más resultados...