Mapa de argumentos

Un mapa de argumentos o diagrama de argumentos es una representación visual de la estructura de un argumento. Un mapa de argumento normalmente incluye los componentes clave del argumento, tradicionalmente llamados conclusión y premisas, también llamados argumento y razones. Los mapas de argumentos también pueden mostrar premisas compartidas, objeciones, contraargumentos, refutaciones y lemas. Hay diferentes estilos de mapas de argumentos, pero a menudo son funcionalmente equivalentes y representan las afirmaciones individuales de un argumento y las relaciones entre ellos.

Los mapas de argumentos se usan comúnmente en el contexto de la enseñanza y la aplicación del pensamiento crítico. El propósito del mapeo es descubrir la estructura lógica de los argumentos, identificar suposiciones no declaradas, evaluar el apoyo que ofrece un argumento para una conclusión y ayudar a comprender los debates. Los mapas de argumentos a menudo están diseñados para apoyar la deliberación de problemas, ideas y argumentos en problemas complicados.

Un mapa de argumentos no debe confundirse con un mapa conceptual o un mapa mental, otros dos tipos de diagramas de nodo-vínculo que tienen diferentes restricciones en nodos y enlaces.

Características clave

Se han propuesto varios tipos diferentes de mapas de argumentos, pero el más común, que Chris Reed y Glenn Rowe llamaron el diagrama estándar, consiste en una estructura de árbol con cada una de las razones que conducen a la conclusión. No hay consenso sobre si la conclusión debe estar en la parte superior del árbol con las razones que conducen a ella o si debe estar en la parte inferior con las razones que conducen a ella. Otra variación diagrama un argumento de izquierda a derecha.

De acuerdo con Douglas N. Walton y sus colegas, un mapa de argumentos tiene dos componentes básicos: "Un componente es un conjunto de números en círculos ordenados como puntos. Cada número representa una proposición (premisa o conclusión) en el argumento que se está diagramando. El otro componente es un conjunto de líneas o flechas que unen los puntos. Cada línea (flecha) representa una inferencia. Toda la red de puntos y líneas representa una especie de descripción general del razonamiento en el argumento dado..." Con la introducción del software para producir argumentos mapas, se ha vuelto común que los mapas de argumentos consistan en cuadros que contienen las proposiciones reales en lugar de números que hacen referencia a esas proposiciones.

Existe desacuerdo sobre la terminología que se debe usar al describir los mapas de argumentos, pero el diagrama estándar contiene las siguientes estructuras:

Premisas dependientes o co-premisas, donde al menos una de las premisas unidas requiere otra premisa antes de que pueda dar soporte a la conclusión: Un argumento con esta estructura ha sido llamado argumento enlazado.

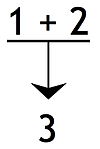Las declaraciones 1 y 2 son premisas dependientes o co-premisas

Premisas independientes, donde la premisa puede respaldar la conclusión por sí sola: aunque las premisas independientes pueden hacer que la conclusión sea más convincente en conjunto, esto debe distinguirse de las situaciones en las que una premisa no brinda respaldo a menos que esté unida a otra premisa. Cuando varias premisas o grupos de premisas conducen a una conclusión final, el argumento puede describirse como convergente. Esto se distingue de un argumento divergente en el que se puede usar una sola premisa para respaldar dos conclusiones separadas.

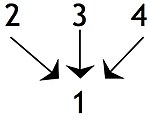Las declaraciones 2, 3, 4 son premisas independientes

Conclusiones intermedias o subconclusiones, donde una afirmación está respaldada por otra afirmación que se utiliza a su vez para respaldar otra afirmación, es decir, la conclusión final u otra conclusión intermedia: En el siguiente diagrama, la declaración 4 es una conclusión intermedia en el sentido de que es una conclusión en relación con el enunciado 5 pero es una premisa en relación con la conclusión final, es decir, el enunciado 1. Un argumento con esta estructura a veces se denomina argumento complejo. Si hay una sola cadena de afirmaciones que contiene al menos una conclusión intermedia, el argumento a veces se describe como un argumento en serie o un argumento en cadena.

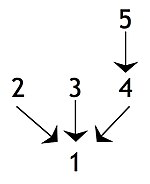La declaración 4 es una conclusión intermedia o una subconclusión

Cada una de estas estructuras se puede representar mediante el enfoque equivalente de "caja y línea" a los mapas de argumentos. En el siguiente diagrama, la afirmación se muestra en la parte superior y los recuadros vinculados a ella representan razones de apoyo, que comprenden una o más premisas. La flecha verde indica que las dos razones apoyan la afirmación:

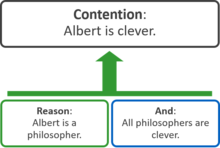Un diagrama de caja y línea

Los mapas de argumentos también pueden representar contraargumentos. En el siguiente diagrama, las dos objeciones debilitan el argumento, mientras que las razones apoyan la premisa de la objeción:

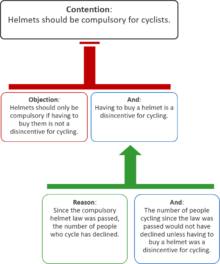Un ejemplo de argumento usando objeciones

Representar un argumento como un mapa de argumentos

Diagramación de texto escrito

Un texto escrito puede transformarse en un mapa argumental siguiendo una secuencia de pasos. El libro Practical Logic de Monroe Beardsley de 1950 recomendaba el siguiente procedimiento:

1. Separe los enunciados entre paréntesis y numérelos.
2. Ponga círculos alrededor de los indicadores lógicos.
3. Proporcione, entre paréntesis, cualquier indicador lógico que se haya omitido.
4. Expón las declaraciones en un diagrama en el que las flechas muestran las relaciones entre las declaraciones.

Beardsley dio el primer ejemplo de un texto analizado de esta manera:Aunque ① [ a las personas que hablan sobre el "significado social" de las artes no les gusta admitirlo ], ② [ la música y la pintura están destinadas a sufrir cuando se convierten en meros vehículos de propaganda ]. Para ③ [ la propaganda apela a los sentimientos más crudos y vulgares ]: (para) ④ [ mira las monstruosidades académicas producidas por los pintores nazis oficiales ]. Lo que es más importante, ⑤ [ el arte debe ser un fin en sí mismo para el artista ], porque ⑥ [ el artista puede hacer el mejor trabajo solo en una atmósfera de completa libertad ].

Beardsley dijo que la conclusión en este ejemplo es la afirmación ②. La declaración ④ debe reescribirse como una oración declarativa, por ejemplo, "las monstruosidades académicas [fueron] producidas por los pintores nazis oficiales". La declaración ① señala que la conclusión no es aceptada por todos, pero la declaración ① se omite del diagrama porque no respalda la conclusión. Beardsley dijo que la relación lógica entre el enunciado ③ y el enunciado ④ no está clara, pero propuso diagramar el enunciado ④ como enunciado de respaldo ③.

Más recientemente, la profesora de filosofía Maralee Harrell recomendó el siguiente procedimiento:

1. Identifique todas las afirmaciones hechas por el autor.
2. Vuelva a escribirlas como declaraciones independientes, eliminando las palabras no esenciales.
3. Identifique qué enunciados son premisas, subconclusiones y la conclusión principal.
4. Proporcione conclusiones implícitas faltantes y premisas implícitas. (Esto es opcional según el propósito del mapa de argumentos).
5. Coloque las declaraciones en cuadros y dibuje una línea entre los cuadros que están vinculados.
6. Indique el apoyo de la(s) premisa(s) a la (sub)conclusión con flechas.

Diagramar como pensar

Los mapas de argumentos son útiles no solo para representar y analizar escritos existentes, sino también para pensar en cuestiones como parte de un proceso de estructuración de problemas o un proceso de escritura. El uso de tal análisis de argumentos para pensar a través de los problemas se ha denominado "argumentación reflexiva".

Un mapa de argumentos, a diferencia de un árbol de decisiones, no dice cómo tomar una decisión, pero el proceso de elegir una posición coherente (o equilibrio reflexivo) basado en la estructura de un mapa de argumentos puede representarse como un árbol de decisiones.

Historia

Los orígenes filosóficos y la tradición del mapeo de argumentos

En Elements of Logic, publicado en 1826 y publicado en muchas ediciones posteriores, el arzobispo Richard Whately dio probablemente la primera forma de un mapa de argumentos, introduciéndolo con la sugerencia de que "muchos estudiantes probablemente encontrarán que es un modo muy claro y conveniente de exhibir el análisis lógico del curso del argumento, para dibujarlo en forma de Árbol, o División Lógica".

Sin embargo, la técnica no llegó a ser ampliamente utilizada, posiblemente porque para argumentos complejos, implicaba mucho escribir y reescribir las premisas.

El filósofo y teórico del derecho John Henry Wigmore produjo mapas de argumentos legales usando premisas numeradas a principios del siglo XX, basándose en parte en las ideas del filósofo del siglo XIX Henry Sidgwick, quien usó líneas para indicar relaciones entre términos.

Diagramación de argumentos anglófonos en el siglo XX

Al lidiar con el fracaso de la reducción formal de la argumentación informal, la teoría de la argumentación de habla inglesa desarrolló enfoques esquemáticos para el razonamiento informal durante un período de cincuenta años.

Monroe Beardsley propuso una forma de diagrama de argumento en 1950. Su método de marcar un argumento y representar sus componentes con números vinculados se convirtió en un estándar y todavía se usa ampliamente. También introdujo terminología que todavía está vigente para describir argumentos convergentes, divergentes y seriales.

Stephen Toulmin, en su innovador e influyente libro de 1958 The Uses of Argument, identificó varios elementos de un argumento que se han generalizado. El diagrama de Toulmin es ampliamente utilizado en la enseñanza crítica educativa.Si bien Toulmin finalmente tuvo un impacto significativo en el desarrollo de la lógica informal, tuvo poco impacto inicial y el enfoque de Beardsley para diagramar argumentos junto con sus desarrollos posteriores se convirtió en el enfoque estándar en este campo. Toulmin introdujo algo que faltaba en el enfoque de Beardsley. En Beardsley, "las flechas unen razones y conclusiones (pero) no se da apoyo a la implicación misma entre ellas. No hay teoría, en otras palabras, de inferencia distinta de la deducción lógica, el pasaje siempre se considera no controvertido y no sujeto a apoyo y evaluación". Toulmin introdujo el concepto de garantía que "puede considerarse como la representación de las razones detrás de la inferencia, el respaldo que autoriza el vínculo".

El enfoque de Beardsley fue refinado por Stephen N. Thomas, cuyo libro de 1973 Razonamiento práctico en lenguaje natural introdujo el término vinculado para describir argumentos en los que las premisas necesariamente trabajaban juntas para respaldar la conclusión. Sin embargo, la distinción real entre premisas dependientes e independientes se había hecho antes de esto. La introducción de la estructura vinculada hizo posible que los mapas de argumentos representaran premisas faltantes u "ocultas". Además, Thomas sugirió mostrar razones tanto a favor como en contra de una conclusión con las razones en contra representadas por flechas punteadas. Thomas introdujo el término diagrama de argumentos y definiórazones básicas como aquellas que no fueron respaldadas por ninguna otra en el argumento y la conclusión final como aquella que no se usó para respaldar ninguna conclusión posterior.

Michael Scriven desarrolló aún más el enfoque de Beardsley-Thomas en su libro Razonamiento de 1976. Mientras que Beardsley había dicho: "Al principio, escriba las declaraciones... después de un poco de práctica, refiérase a las declaraciones solo por número", Scriven abogó por aclarar el significado de las declaraciones, enumerarlas y luego usar un diagrama de árbol con números para mostrar el estructura. Las premisas faltantes (suposiciones no declaradas) debían incluirse e indicarse con una letra alfabética en lugar de un número para marcarlas de las declaraciones explícitas. Scriven introdujo contraargumentos en sus diagramas, que Toulmin había definido como refutación. Esto también permitió la diagramación de argumentos de "equilibrio de consideración".

En 1998, una serie de mapas de argumentos a gran escala publicados por Robert E. Horn estimuló un interés generalizado en el mapeo de argumentos.

Desarrollo de visualización de argumentos asistida por ordenador

El pionero de la interacción humano-computadora, Douglas Engelbart, en un famoso informe técnico de 1962 sobre el aumento de la inteligencia, imaginó en detalle algo así como un software de mapeo de argumentos como parte integral de las futuras interfaces de computadora que aumentan la inteligencia:

Por lo general, piensa en un argumento como una secuencia en serie de pasos de la razón, que comienza con hechos conocidos, suposiciones, etc., y avanza hacia una conclusión. Bueno, tenemos que pensar en estos pasos en serie, y generalmente enumeramos los pasos en serie cuando los escribimos porque esa es más o menos la forma en que nuestros artículos y libros tienen que presentarlos: son bastante limitantes en el símbolo que estructuran. permitirnos usar.... Para ayudarnos a obtener una mejor comprensión de la estructura de un argumento, también podemos invocar una visualización esquemática o gráfica. Una vez que se han establecido los vínculos antecedente-consecuente, la computadora puede construir automáticamente tal pantalla para nosotros.—  Douglas Engelbart, "Aumentar el intelecto humano: un marco conceptual" (1962)

A mediados y finales de la década de 1980, se desarrollaron aplicaciones de software de hipertexto que admitían la visualización de argumentos, incluidas NoteCards y gIBIS; este último generó un mapa hipertextual gráfico en pantalla de un sistema de información basado en problemas, un modelo de argumentación desarrollado por Werner Kunz y Horst Rittel en la década de 1970. En la década de 1990, Tim van Gelder y sus colegas desarrollaron una serie de aplicaciones de software que permitieron que las premisas de un mapa de argumentos se enunciaran y editaran completamente en el diagrama, en lugar de en una leyenda. El primer programa de Van Gelder, Reason!Able, fue reemplazado por dos programas posteriores, bCisive y Rationale.

A lo largo de las décadas de 1990 y 2000, se desarrollaron muchas otras aplicaciones de software para la visualización de argumentos. Para 2013, existían más de 60 de estos sistemas de software. En una encuesta de 2010 sobre argumentación asistida por computadora, Oliver Scheuer y sus colegas notaron que una de las diferencias entre estos sistemas de software es si se admite la colaboración. En su encuesta, los sistemas de argumentación de un solo usuario incluyeron Convince Me, iLogos, LARGO, Athena, Araucaria y Carneades; los sistemas de argumentación de grupos pequeños incluyeron Digalo, QuestMap, Compendium, Belvedere y AcademicTalk; los sistemas de argumentación comunitaria incluyeron Debategraph y Collaboratorium.

Aplicaciones

Los mapas de argumentos se han aplicado en muchas áreas, pero sobre todo en entornos educativos, académicos y empresariales, incluida la justificación del diseño. Los mapas de argumentos también se utilizan en ciencia forense, derecho e inteligencia artificial. También se ha propuesto que el mapeo de argumentos tiene un gran potencial para mejorar la forma en que entendemos y ejecutamos la democracia, en referencia a la evolución en curso de la e-democracia.

Dificultades con la tradición filosófica

Tradicionalmente, ha sido difícil separar la enseñanza del pensamiento crítico de la tradición filosófica de la enseñanza de la lógica y el método, y la mayoría de los libros de texto de pensamiento crítico han sido escritos por filósofos. Los libros de texto de lógica informal están repletos de ejemplos filosóficos, pero no está claro si el enfoque en dichos libros de texto se transfiere a estudiantes que no son de filosofía. Parece haber poco efecto estadístico después de tales clases. Sin embargo, el mapeo de argumentos tiene un efecto medible según muchos estudios. Por ejemplo, se ha demostrado que la instrucción en el mapeo de argumentos mejora las habilidades de pensamiento crítico de los estudiantes de negocios.

Evidencia de que el mapeo de argumentos mejora la capacidad de pensamiento crítico

Existe evidencia empírica de que las habilidades desarrolladas en los cursos de pensamiento crítico basados ​​en el mapeo de argumentos se transfieren sustancialmente al pensamiento crítico realizado sin mapas de argumentos. El metanálisis de Álvarez encontró que tales cursos de pensamiento crítico produjeron ganancias de alrededor de 0,70 SD, aproximadamente el doble que los cursos estándar de pensamiento crítico. Las pruebas utilizadas en los estudios revisados ​​eran pruebas estándar de pensamiento crítico.

Limitaciones

Cuando se usan con estudiantes en la escuela, los mapas de argumentos tienen limitaciones. Pueden "terminar pareciendo demasiado complejos" y pueden aumentar la carga cognitiva más allá de lo que es óptimo para aprender el contenido del curso. La creación de mapas requiere un amplio entrenamiento y comentarios de un mapeador de argumentos experimentado. Dependiendo de los objetivos de aprendizaje, el tiempo dedicado a entrenar a los estudiantes para crear buenos mapas puede emplearse mejor aprendiendo el contenido del curso en lugar de aprender a diagramar. Cuando el objetivo es incitar a los estudiantes a considerar otras perspectivas y contraargumentos, el objetivo puede lograrse más fácilmente con otros métodos, como debates, rúbricas y un marco de argumento simple o un organizador gráfico simple, como un diagrama en V.Para maximizar las fortalezas del mapeo de argumentos y minimizar sus limitaciones en el aula, se requiere considerar en qué punto de una progresión de aprendizaje los beneficios potenciales del mapeo de argumentos superarían sus posibles desventajas.

Estándares

Formato de intercambio de argumentos

El formato de intercambio de argumentos, AIF, es un esfuerzo internacional para desarrollar un mecanismo de representación para intercambiar recursos de argumentos entre grupos de investigación, herramientas y dominios utilizando un lenguaje semánticamente rico. AIF-RDF es la ontología extendida representada en el lenguaje semántico Resource Description Framework Schema (RDFS). Aunque AIF sigue siendo algo así como un objetivo en movimiento, se está asentando.

Formato de intercambio de conocimientos jurídicos

El Formato de Intercambio de Conocimiento Legal (LKIF) fue desarrollado en el proyecto europeo ESTRELLA y diseñado con el objetivo de convertirse en un estándar para representar e intercambiar políticas, leyes y casos, incluidos sus argumentos justificativos, en el ámbito legal. LKIF se basa y utiliza el lenguaje de ontología web (OWL) para representar conceptos e incluye una ontología básica reutilizable de conceptos legales.

Arg abajo

Argdown es un lenguaje de marcado ligero inspirado en Markdown para argumentaciones complejas. Está destinado a intercambiar argumentos y reconstrucciones de argumentos de una manera universalmente accesible y altamente legible por humanos. La sintaxis de Argdown se acompaña de herramientas que facilitan la codificación y transforman los documentos de Argdown en mapas de argumentos.