Magnitud aparente
Magnitud aparente (m) es una medida de la brillo de una estrella u otro objeto astronómico observado desde la Tierra. La magnitud aparente de un objeto depende de su luminosidad intrínseca, su distancia a la Tierra y cualquier extinción de la luz del objeto causada por el polvo interestelar a lo largo de la línea de visión del observador.
La palabra magnitud en astronomía, a menos que se indique lo contrario, generalmente se refiere a la magnitud aparente de un objeto celeste. La escala de magnitud se remonta al antiguo astrónomo romano Claudio Ptolomeo, cuyo catálogo de estrellas enumeró estrellas desde la primera magnitud (más brillante) hasta la sexta magnitud (más tenue). La escala moderna se definió matemáticamente de manera que coincidiera estrechamente con este sistema histórico.
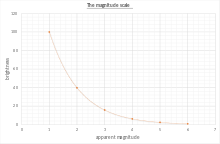
La escala es logarítmica inversa: cuanto más brillante es un objeto, menor es su número de magnitud. Una diferencia de 1.0 en magnitud corresponde a una relación de brillo 1005{displaystyle {sqrt[{5}{100}}, o alrededor de 2.512. Por ejemplo, una estrella de magnitud 2.0 es 2,512 veces tan brillante como una estrella de magnitud 3.0, 6.31 veces tan brillante como una estrella de magnitud 4.0, y 100 veces tan brillante como una de magnitud 7.0.
Los objetos astronómicos más brillantes tienen magnitudes aparentes negativas: por ejemplo, Venus en −4,2 o Sirio en −1,46. Las estrellas más débiles visibles a simple vista en la noche más oscura tienen magnitudes aparentes de aproximadamente +6,5, aunque esto varía según la vista de una persona y la altitud y las condiciones atmosféricas. Las magnitudes aparentes de los objetos conocidos van desde el Sol en −26,832 hasta objetos en imágenes profundas del telescopio espacial Hubble de magnitud +31,5.
La medida de la magnitud aparente se llama fotometría. Las mediciones fotométricas se realizan en las bandas de longitud de onda ultravioleta, visible o infrarroja utilizando filtros de banda de paso estándar pertenecientes a sistemas fotométricos como el sistema UBV o el sistema Strömgren uvbyβ.
La magnitud absoluta es una medida de la luminosidad intrínseca de un objeto celeste, en lugar de su brillo aparente, y se expresa en la misma escala logarítmica inversa. La magnitud absoluta se define como la magnitud aparente que tendría una estrella u objeto si se observara desde una distancia de 10 parsecs (33 años luz; 3,1× 1014 kilómetros; 1,9×1014 millas). Por tanto, es de mayor utilidad en astrofísica estelar ya que hace referencia a una propiedad de una estrella independientemente de lo cerca que esté de la Tierra. Pero en la astronomía observacional y la observación popular de estrellas, las referencias incondicionales a la "magnitud" se entiende que significan magnitud aparente.
Historia
| Visible a típico humanos ojo | Apparent magnitud | Brillante... ness relativo a Vega | Número de estrellas (excepto el Sol) más brillante que magnitud aparente en el cielo nocturno |
|---|---|---|---|
| Sí. | 1.0− | 251% | 1 (Sirius) |
| 00,0 | 100% | 4 | |
| 01.0 | 40% | 15 | |
| 02.0 | 16% | 48 | |
| 03.0 | 6,3% | 171 | |
| 04.0 | 2.5% | 513 | |
| 05.0 | 1.0% | 1602 | |
| 06.0 | 0,4% | 4800 | |
| 06.5 | 0,25% | 9100 | |
| No | 07.0 | 0,16% | 14000 |
| 08.0 | 0,063% | 42000 | |
| 09.0 | 0,025% | 121000 | |
| 10.0 | 0,010% | 340000 |
La escala utilizada para indicar la magnitud tiene su origen en la práctica helenística de dividir las estrellas visibles a simple vista en seis magnitudes. Se decía que las estrellas más brillantes del cielo nocturno eran de primera magnitud (m = 1), mientras que las más débiles eran de sexta magnitud (m = 6), que es el límite de la percepción visual humana (sin la ayuda de un telescopio). Cada grado de magnitud se consideró el doble del brillo del grado siguiente (una escala logarítmica), aunque esa proporción era subjetiva ya que no existían fotodetectores. Esta escala bastante tosca para el brillo de las estrellas fue popularizada por Ptolomeo en su Almagesto y generalmente se cree que se originó con Hiparco. Esto no se puede probar ni refutar porque el catálogo de estrellas original de Hiparco se ha perdido. El único texto conservado del propio Hipparchus (un comentario a Aratus) documenta claramente que no tenía un sistema para describir el brillo con números: siempre usa términos como "grande" o "pequeño", "brillante" o "desmayo" o incluso descripciones como "visible en luna llena".
En 1856, Norman Robert Pogson formalizó el sistema al definir una estrella de primera magnitud como una estrella que es 100 veces más brillante que una estrella de sexta magnitud, estableciendo así la escala logarítmica que todavía se usa en la actualidad. Esto implica que una estrella de magnitud m es aproximadamente 2,512 veces más brillante que una estrella de magnitud m + 1. Esta cifra, la quinta raíz de 100, se conoció como la Razón de Pogson. El punto cero de la escala de Pogson se definió originalmente asignando a Polaris una magnitud de exactamente 2. Más tarde, los astrónomos descubrieron que Polaris es ligeramente variable, por lo que cambiaron a Vega como la estrella de referencia estándar, asignando el brillo de Vega como definición. de magnitud cero en cualquier longitud de onda especificada.
Aparte de pequeñas correcciones, el brillo de Vega todavía sirve como definición de magnitud cero para longitudes de onda visibles e infrarrojas cercanas, donde su distribución de energía espectral (SED) se aproxima mucho a la de un cuerpo negro para una temperatura de 11000 K. Sin embargo, con el advenimiento de la astronomía infrarroja se reveló que la radiación de Vega incluye un exceso de infrarrojo presumiblemente debido a un disco circunestelar que consiste en polvo a temperaturas cálidas (pero mucho más frío que la superficie de la estrella). En longitudes de onda más cortas (por ejemplo, visibles), hay una emisión insignificante del polvo a estas temperaturas. Sin embargo, para extender adecuadamente la escala de magnitud más allá del infrarrojo, esta peculiaridad de Vega no debería afectar la definición de la escala de magnitud. Por lo tanto, la escala de magnitud se extrapoló a todas longitudes de onda sobre la base de la curva de radiación de cuerpo negro para una superficie estelar ideal en 11000 K sin contaminación por radiación circunestelar. Sobre esta base, se puede calcular la irradiancia espectral (generalmente expresada en janskys) para el punto de magnitud cero, en función de la longitud de onda. Se especifican pequeñas desviaciones entre sistemas que utilizan aparatos de medición desarrollados independientemente para que los datos obtenidos por diferentes astrónomos puedan compararse adecuadamente, pero de mayor importancia práctica es la definición de magnitud no en una sola longitud de onda sino que se aplica a la respuesta de filtros espectrales estándar utilizados en fotometría. en varias bandas de longitud de onda.
| Telescopio aperture (mm) | Limitación Magnitud |
|---|---|
| 35 | 11.3 |
| 60 | 12.3 |
| 102 | 13.3 |
| 152 | 14.1 |
| 203 | 14.7 |
| 305 | 15.4 |
| 406 | 15.7 |
| 508 | 16.4 |
Con los sistemas de magnitud modernos, el brillo en un rango muy amplio se especifica de acuerdo con la definición logarítmica que se detalla a continuación, utilizando esta referencia cero. En la práctica, tales magnitudes aparentes no exceden de 30 (para mediciones detectables). El brillo de Vega es superado por cuatro estrellas en el cielo nocturno en longitudes de onda visibles (y más en longitudes de onda infrarrojas), así como por los brillantes planetas Venus, Marte y Júpiter, y estos deben describirse como negativos. magnitudes Por ejemplo, Sirio, la estrella más brillante de la esfera celeste, tiene una magnitud de −1,4 en el visible. Las magnitudes negativas de otros objetos astronómicos muy brillantes se pueden encontrar en la siguiente tabla.
Los astrónomos han desarrollado otros sistemas fotométricos de punto cero como alternativas al sistema Vega. El más utilizado es el sistema de magnitud AB, en el que los puntos cero fotométricos se basan en un espectro de referencia hipotético que tiene un flujo constante por unidad de intervalo de frecuencia, en lugar de utilizar un espectro estelar o una curva de cuerpo negro como referencia. El punto cero de la magnitud AB se define de tal manera que las magnitudes basadas en AB y Vega de un objeto serán aproximadamente iguales en la banda del filtro V.
Medición
La medición de precisión de la magnitud (fotometría) requiere la calibración del aparato de detección fotográfico o (normalmente) electrónico. Esto generalmente implica la observación contemporánea, en condiciones idénticas, de estrellas estándar cuya magnitud se conoce con precisión utilizando ese filtro espectral. Además, como la cantidad de luz que realmente recibe un telescopio se reduce debido a la transmisión a través de la atmósfera terrestre, se deben tener en cuenta las masas de aire de las estrellas objetivo y de calibración. Por lo general, uno observaría algunas estrellas diferentes de magnitud conocida que son suficientemente similares. Se prefieren las estrellas calibradoras cercanas en el cielo al objetivo (para evitar grandes diferencias en las trayectorias atmosféricas). Si esas estrellas tienen ángulos cenitales algo diferentes (altitudes), entonces se puede derivar un factor de corrección en función de la masa de aire y aplicarlo a la masa de aire en la posición del objetivo. Tal calibración obtiene el brillo que se observaría desde arriba de la atmósfera, donde se define la magnitud aparente.
Para los principiantes en astronomía, la magnitud aparente escala con la potencia recibida (a diferencia de la amplitud), por lo que para la astrofotografía puede usar la medida de brillo relativo para escalar los tiempos de exposición entre estrellas. La magnitud aparente también se suma (integra) sobre todo el objeto, por lo que es independiente del foco. Esto debe tenerse en cuenta al escalar los tiempos de exposición de objetos con un tamaño aparente significativo, como el Sol, la Luna y los planetas. Por ejemplo, escalar directamente el tiempo de exposición de la Luna al Sol funciona, porque tienen aproximadamente el mismo tamaño en el cielo, pero escalar la exposición de la Luna a Saturno daría como resultado una sobreexposición, si la imagen de Saturno ocupa una área más pequeña en su sensor que la Luna (con el mismo aumento o más generalmente f/#).
Cálculos
Cuanto más tenue aparece un objeto, mayor es el valor numérico dado a su magnitud, con una diferencia de 5 magnitudes que corresponde a un factor de brillo de exactamente 100. Por lo tanto, la magnitud m, en la banda espectral x, estaría dada por
Ejemplo: Sol y Luna
¿Cuál es la relación de brillo entre el Sol y la Luna llena?
La magnitud aparente del Sol es −26,832 (más brillante) y la magnitud media de la luna llena es −12,74 (más tenue).
Diferencia en magnitud:
Factor de brillo:
El Sol aparece sobre 400000 veces más brillante que la Luna llena.
Suma de magnitudes
A veces uno podría desear agregar brillo. Por ejemplo, es posible que la fotometría en estrellas dobles muy separadas solo pueda producir una medición de su salida de luz combinada. Para encontrar la magnitud combinada de esa estrella doble conociendo solo las magnitudes de los componentes individuales, esto se puede hacer sumando el brillo (en unidades lineales) correspondiente a cada magnitud.
Solving for mf{displaystyle m_{f} rendimientos
Magnitud bolométrica aparente
Mientras que la magnitud generalmente se refiere a una medición en una banda de filtro particular correspondiente a algún rango de longitudes de onda, la magnitud bolométrica aparente o absoluta (mbol) es una medida de el brillo absoluto o aparente de un objeto integrado en todas las longitudes de onda del espectro electromagnético (también conocido como irradiancia o potencia del objeto, respectivamente). El punto cero de la escala de magnitud bolométrica aparente se basa en la definición de que una magnitud bolométrica aparente de 0 mag equivale a una irradiación recibida de 2,518×10−8 vatios por metro cuadrado (W·m−2).
Magnitud absoluta
Mientras que la magnitud aparente es una medida del brillo de un objeto visto por un observador en particular, la magnitud absoluta es una medida del brillo intrínseco de un objeto. El flujo disminuye con la distancia según la ley del inverso del cuadrado, por lo que la magnitud aparente de una estrella depende tanto de su brillo absoluto como de su distancia (y de cualquier extinción). Por ejemplo, una estrella a una distancia tendrá la misma magnitud aparente que una estrella cuatro veces más brillante al doble de esa distancia. En cambio, el brillo intrínseco de un objeto astronómico, no depende de la distancia del observador ni de extinción alguna.
La magnitud absoluta M de una estrella u objeto astronómico se define como la magnitud aparente que tendría vista desde un distancia de 10 parsecs (33 ly). La magnitud absoluta del Sol es 4,83 en la banda V (visual), 4,68 en la banda G del satélite Gaia (verde) y 5,48 en la banda B (azul).
En el caso de un planeta o asteroide, la magnitud absoluta H significa más bien la magnitud aparente que tendría si fuera 1 unidad astronómica (150 000 000 km) tanto del observador como del Sol, y completamente iluminada en la máxima oposición (una configuración que solo se puede lograr teóricamente, con el observador situado en la superficie del Sol).
Valores de referencia estándar
| Banda | λ (μm) | Δλ/λ (FWHM) | Flux en m = 0, Fx,0 | |
|---|---|---|---|---|
| Jy | 1020 - 20erg/(s·cm)2·Hz) | |||
| U | 0.36 | 0.15 | 1810 | 1.81 |
| B | 0.44 | 0.22 | 4260 | 4.26 |
| V | 0,555 | 0.16 | 3640 | 3.64 |
| R | 0,644 | 0.23 | 3080 | 3.08 |
| I | 0,79 | 0.19 | 2550 | 2.55 |
| J | 1.26 | 0.16 | 1600 | 1.60 |
| H | 1.60 | 0.23 | 1080 | 1.08 |
| K | 2.22 | 0.23 | 0670 | 0,677 |
| L | 3.50 | |||
| g | 0,522 | 0.14 | 3730 | 3.73 |
| r | 0,677 | 0.14 | 4490 | 4.49 |
| i | 0,79 | 0.16 | 4760 | 4.76 |
| z | 0.91 | 0,13 | 4810 | 4.81 |
La escala de magnitud es una escala logarítmica inversa. Un concepto erróneo común es que la naturaleza logarítmica de la escala se debe a que el propio ojo humano tiene una respuesta logarítmica. En la época de Pogson, se pensaba que esto era cierto (consulte la ley de Weber-Fechner), pero ahora se cree que la respuesta es una ley de potencia .
La magnitud se complica por el hecho de que la luz no es monocromática. La sensibilidad de un detector de luz varía según la longitud de onda de la luz, y la forma en que varía depende del tipo de detector de luz. Por esta razón, es necesario especificar cómo se mide la magnitud para que el valor sea significativo. Para ello se utiliza ampliamente el sistema UBV, en el que la magnitud se mide en tres bandas de longitud de onda diferentes: U (centrado a unos 350 nm, en el ultravioleta cercano), B (alrededor de 435 nm, en la región azul) y V (aproximadamente 555 nm, en el medio del rango visual humano a la luz del día). La banda V se eligió con fines espectrales y proporciona magnitudes que se corresponden estrechamente con las vistas por el ojo humano. Cuando se discute una magnitud aparente sin mayor calificación, generalmente se entiende la magnitud V.
Debido a que las estrellas más frías, como las gigantes rojas y las enanas rojas, emiten poca energía en las regiones azul y ultravioleta del espectro, su poder suele estar subrepresentado en la escala UBV. De hecho, algunas estrellas de clase L y T tienen una magnitud estimada de más de 100, porque emiten muy poca luz visible, pero son más intensas en el infrarrojo.
Las medidas de magnitud necesitan un tratamiento cauteloso y es extremadamente importante medir lo similar. En películas fotográficas ortocromáticas (sensibles al azul) de principios del siglo XX y más antiguas, los brillos relativos de la supergigante azul Rigel y la estrella variable irregular supergigante roja Betelgeuse (al máximo) se invierten en comparación con lo que perciben los ojos humanos, porque esta película arcaica es más más sensible a la luz azul que a la luz roja. Las magnitudes obtenidas con este método se conocen como magnitudes fotográficas y ahora se consideran obsoletas.
Para los objetos dentro de la Vía Láctea con una magnitud absoluta dada, se suma 5 a la magnitud aparente por cada aumento de diez veces en la distancia al objeto. Para objetos a distancias muy grandes (mucho más allá de la Vía Láctea), esta relación debe ajustarse para desplazamientos al rojo y para medidas de distancia no euclidianas debido a la relatividad general.
Para los planetas y otros cuerpos del Sistema Solar, la magnitud aparente se deriva de su curva de fase y las distancias al Sol y al observador.
Lista de magnitudes aparentes
Algunas de las magnitudes enumeradas son aproximadas. La sensibilidad del telescopio depende del tiempo de observación, el paso de banda óptico y la luz que interfiere debido a la dispersión y el resplandor del aire.
| Apparent magnitud (V) | Objeto | Visto de... | Notas |
|---|---|---|---|
| 67−57 | GRB 080319B | visto desde 1 AU lejos | Habría terminado 2×1016 (20 quadrillion) tiempos tan brillantes como el Sol cuando se ve desde la Tierra |
| −41.39 | estrella Cygnus OB2-12 | visto desde 1 AU lejos | |
| −40,67 | star M33-013406.63 | visto desde 1 AU lejos | |
| –40.17 | estrella Eta Carinae A | visto desde 1 AU lejos | |
| −40.07 | estrella Zeta1 Scorpii | visto desde 1 AU lejos | |
| −39.66 | estrella R136a1 | visto desde 1 AU lejos | |
| –39.47 | estrella P Cygni | visto desde 1 AU lejos | |
| −38.00 | estrella Rigel | visto desde 1 AU lejos | sería visto como un disco grande, muy brillante azulado de 35° diámetro aparente |
| 30 - 30 | estrella Sirius A | visto desde 1 AU lejos | |
| −29.30 | estrella Sun | visto desde Mercurio en perihelion | |
| −27.40 | estrella Sun | visto desde Venus en perihelion | |
| −26 - 832 | estrella Sun | visto desde la Tierra | alrededor de 400.000 veces tan brillante como la luna llena |
| 25 - 60 | estrella Sun | visto desde Marte en Aphelion | |
| −25.00 | El brillo mínimo que causa el dolor típico del ojo para mirar | ||
| 23−00 | estrella Sun | visto desde Júpiter en Aphelion | |
| −21,70 | estrella Sun | visto desde Saturno en aphelion | |
| 20 a 20 años | estrella Sun | visto desde Urano en aphelion | |
| −19.30 | estrella Sun | visto desde Neptuno | |
| −18.20 | estrella Sun | visto desde Plutón en aphelion | |
| −17.70 | planeta Tierra | visto como la luz de la luna | |
| −16.70 | estrella Sun | visto desde Eris en aphelion | |
| −14.20 | Nivel de iluminación de 1 lux | ||
| −12,90 | Luna llena | visto desde la Tierra en el perihelio | brillo máximo de perigeo + perihelio + Luna llena (valor de distancia medio es −12.74, aunque los valores son aproximadamente 0.18 magnitud más brillante cuando se incluye el efecto de oposición) |
| −12.40 | Betelgeuse | visto desde la Tierra cuando va supernova | |
| −11.20 | estrella Sun | visto desde Sedna en aphelion | |
| −10.00 | Comet Ikeya–Seki (1965) | visto desde la Tierra | que era el más brillante Kreutz Sungrazer de los tiempos modernos |
| −9.50 | Iridium (satélite) flare | visto desde la Tierra | brillo máximo |
| 9 a 10 | Phobos (luna) | visto desde Marte | brillo máximo |
| −7.50 | supernova de 1006 | visto desde la Tierra | el evento estelar más brillante en la historia registrada (7200 años luz de distancia) |
| −6.50 | La magnitud total integrada del cielo nocturno | visto desde la Tierra | |
| −6.00 | Crab Supernova de 1054 | visto desde la Tierra | (6500 años luz de distancia) |
| 5.90 | Estación Espacial Internacional | visto desde la Tierra | cuando el ISS está en su perigeo y completamente iluminado por el Sol |
| −4.92 | planeta Venus | visto desde la Tierra | brillo máximo cuando se ilumina como una crescente |
| −4.14 | planeta Venus | visto desde la Tierra | significa brillo |
| −4 | Objetos más falsos observables durante el día con ojo desnudo cuando el Sol está alto. Un objeto astronómico arroja sombras humanas visibles cuando su aparente magnitud es igual o inferior a -4 | ||
| −3.99 | estrella Epsilon Canis Majoris | visto desde la Tierra | máximo brillo de hace 4,7 millones de años, la estrella más brillante histórica de los últimos y próximos cinco millones de años. |
| −3.69 | Luna | iluminado por la luz de la tierra, reflejando el brillo de la Tierra (maximum) | |
| −2.98 | planeta Venus | visto desde la Tierra | brillo mínimo cuando está en el lado lejano del Sol |
| −2.94 | planeta Júpiter | visto desde la Tierra | brillo máximo |
| −2.94 | planeta Marte | visto desde la Tierra | brillo máximo |
| −2.5 | Objetos más falsos visibles durante el día con ojo desnudo cuando el Sol está a menos de 10° sobre el horizonte | ||
| −2.50 | nueva luna | visto desde la Tierra | brillo mínimo |
| −2.50 | planeta Tierra | visto desde Marte | brillo máximo |
| −2.48 | Planeta Mercurio | visto desde la Tierra | brillo máximo en conjunción superior (a diferencia de Venus, Mercurio está en su más brillante cuando en el lado lejano del Sol, la razón por la que son sus diferentes curvas de fase) |
| −2.20 | planeta Júpiter | visto desde la Tierra | significa brillo |
| −1.66 | planeta Júpiter | visto desde la Tierra | brillo mínimo |
| −1.47 | Star system Sirius | visto desde la Tierra | Estrella más brillante excepto para el Sol en longitudes de onda visibles |
| −0,83 | estrella Eta Carinae | visto desde la Tierra | brillo aparente como un impostor de supernova en abril de 1843 |
| −0,72 | estrella Canopus | visto desde la Tierra | 2a estrella más brillante en el cielo nocturno |
| −0.55 | planeta Saturno | visto desde la Tierra | máxima luminosidad cerca de la oposición y el perihelio cuando los anillos están inclinados hacia la Tierra |
| −0.3 | El cometa Halley | visto desde la Tierra | magnitud aparente esperada en el pasaje 2061 |
| −0,27 | sistema estelar Alpha Centauri AB | visto desde la Tierra | magnitud combinada (3a estrella más brillante en el cielo nocturno) |
| 0.0−4 | estrella Arcturus | visto desde la Tierra | 4a estrella más brillante al ojo desnudo |
| 0.0−1 | estrella Alpha Centauri A | visto desde la Tierra | 4o más brillante individual estrella visible telescópicamente en el cielo nocturno |
| +0.03 | estrella Vega | visto desde la Tierra | que fue elegido originalmente como una definición del punto cero |
| +0.23 | Planeta Mercurio | visto desde la Tierra | significa brillo |
| +0.46 | estrella Sun | visto desde Alpha Centauri | |
| +0.46 | planeta Saturno | visto desde la Tierra | significa brillo |
| +0.71 | planeta Marte | visto desde la Tierra | significa brillo |
| +0.90 | Luna | visto desde Marte | brillo máximo |
| +1.17 | planeta Saturno | visto desde la Tierra | brillo mínimo |
| +1.33 | estrella Alpha Centauri B | visto desde la Tierra | |
| +1.86 | planeta Marte | visto desde la Tierra | brillo mínimo |
| +1.98 | estrella Polaris | visto desde la Tierra | significa brillo |
| +3.03 | supernova SN 1987A | visto desde la Tierra | en la Gran Nube Magallanes (160,000 años luz de distancia) |
| +3 a +4 | Faintest estrellas visibles en un barrio urbano con ojo desnudo | ||
| +3.44 | Andromeda Galaxy | visto desde la Tierra | M31 |
| +4 | Nebulosa de Orión | visto desde la Tierra | M42 |
| +4.38 | Luna Ganymede | visto desde la Tierra | brillo máximo (luna de Júpiter y la luna más grande del Sistema Solar) |
| +4.50 | grupo abierto M41 | visto desde la Tierra | un clúster abierto que podría haber sido visto por Aristóteles |
| +4.5 | Sagittarius Dwarf Spheroidal Galaxy | visto desde la Tierra | |
| +5.20 | asteroides Vesta | visto desde la Tierra | brillo máximo |
| +5.38 | planeta Urano | visto desde la Tierra | brillo máximo (El Urano llega al perihelio en 2050) |
| +5.68 | planeta Urano | visto desde la Tierra | significa brillo |
| +5.72 | galaxia espiral M33 | visto desde la Tierra | que se utiliza como una prueba para observar a simple vista bajo cielos oscuros |
| +5.8 | GRB 080319B | visto desde la Tierra | Alcanzar la magnitud visual (el "Evento de Calaveras") visto en la Tierra el 19 de marzo de 2008 desde una distancia de 7,5 billones de años luz. |
| +6.03 | planeta Urano | visto desde la Tierra | brillo mínimo |
| +6.49 | asteroide Pallas | visto desde la Tierra | brillo máximo |
| +6.5 | Límite aproximado de estrellas observado por un # observador de ojos desnudos bajo muy buenas condiciones. Hay alrededor de 9.500 estrellas visibles a la revista 6.5. | ||
| +6.64 | enano planeta Ceres | visto desde la Tierra | brillo máximo |
| +6.75 | asteroides Iris | visto desde la Tierra | brillo máximo |
| +6.90 | galaxia espiral M81 | visto desde la Tierra | Este es un extremo de ojos desnudos que empuja la vista humana y la escala Bortle al límite |
| +7.25 | Planeta Mercurio | visto desde la Tierra | brillo mínimo |
| +7.67 | planeta Neptuno | visto desde la Tierra | brillo máximo (Neptuno llega al perihelio en 2042) |
| +7.78 | planeta Neptuno | visto desde la Tierra | significa brillo |
| +8.00 | planeta Neptuno | visto desde la Tierra | brillo mínimo |
| + 8 | Extremo límite de ojo desnudo, Clase 1 en escala Bortle, los cielos más oscuros disponibles en la Tierra. | ||
| +8.10 | Luna Titan | visto desde la Tierra | brillo máximo; luna más grande de Saturno; magnitud de oposición 8.4 |
| +8.29 | estrella UY Scuti | visto desde la Tierra | El brillo máximo; una de las mayores estrellas conocidas por radio |
| +8.94 | asteroide 10 Hygiea | visto desde la Tierra | brillo máximo |
| +9.50 | Objetos más falsos visibles usando binoculares comunes de 7×50 bajo condiciones típicas | ||
| +10.20 | Moon Iapetus | visto desde la Tierra | brillo máximo, más brillante cuando al oeste de Saturno y toma 40 días para cambiar los lados |
| +11.05 | estrella Proxima Centauri | visto desde la Tierra | estrella más cercana |
| +11.8 | luna Phobos | visto desde la Tierra | El brillo máximo; luna más brillante de Marte |
| +12.23 | estrella R136a1 | visto desde la Tierra | estrella más luminosa y masiva conocida |
| +12.89 | luna Deimos | visto desde la Tierra | Luminosidad máxima |
| +12.91 | quasar 3C 273 | visto desde la Tierra | más brillante (la distancia de la luminosidad de 2.4 billones de años luz) |
| +13.42 | Luna Triton | visto desde la Tierra | Luminosidad máxima |
| +13.65 | enano planeta Plutón | visto desde la Tierra | brillo máximo, 725 veces más débil que la magnitud 6.5 cielos de ojos desnudos |
| +13.9 | Luna Titania | visto desde la Tierra | El brillo máximo; luna más brillante de Urano |
| +14.1 | estrella WR 102 | visto desde la Tierra | La estrella más conocida |
| +15.4 | Centaur Chiron | visto desde la Tierra | brillo máximo |
| +15.55 | Luna Charon | visto desde la Tierra | brillo máximo (la luna más grande de Plutón) |
| +16.8 | enano planeta Makemake | visto desde la Tierra | El brillo actual de la oposición |
| +17.27 | enano planeta Haumea | visto desde la Tierra | El brillo actual de la oposición |
| +18.7 | enano planeta Eris | visto desde la Tierra | El brillo actual de la oposición |
| +19.5 | Objetos más falsos observables con el telescopio Catalina Sky Survey 0,7 metros utilizando una exposición de 30 segundos y también la magnitud limitante aproximada de Asteroid Terrestrial-impact Last Alert System (ATLAS) | ||
| +20.7 | Luna Callirrhoe | visto desde la Tierra | (pequeño satélite de 38 km de Júpiter) |
| +22 | Objetos más falsos observables en luz visible con 600 mm (24′) telescopio Ritchey-Chrétien con 30 minutos de imágenes apiladas (6 subframes a 5 minutos cada uno) usando un detector CCD | ||
| +22.8 | Luhman 16 | visto desde la Tierra | Enanas más cercanas (Luhman 16A=23.25, Luhman 16B=24.07) |
| +22.91 | Moon Hydra | visto desde la Tierra | brillo máximo de la luna de Plutón |
| +23.38 | Luna Nix | visto desde la Tierra | brillo máximo de la luna de Plutón |
| +24 | Objetos más falsos observables con el Pan-STARRS Telescopio de 1,8 metros con exposición de 60 segundos Esta es la magnitud límite de las encuestas astronómicas allsky automatizadas. | ||
| +25.0 | Luna Fenrir | visto desde la Tierra | (pequeño satélite de Saturno de 4 km) |
| +25.3 | Objeto trans-neptuniano 2018 AG37 | visto desde la Tierra | Objeto observable más conocido en el Sistema Solar alrededor de 132 AU (19.7 billones de km) del Sol |
| +26.2 | Objeto trans-neptuniano 2015 TH367 | visto desde la Tierra | 200 km de tamaño objeto alrededor de 90 AU (13 billones de km) del Sol y cerca 75 millones de veces más débil que lo que se puede ver con el ojo desnudo. |
| +27.7 | Objetos más falsos observables con un único telescopio basado en tierra de 8 metros de clase, como el Telescopio Subaru en una imagen de 10 horas | ||
| +28.2 | Halley's Comet | visto desde la Tierra (2003) | en 2003 cuando era 28 UA (4.2 mil millones de km) del Sol, imaginado utilizando 3 de 4 alcances individuales sincronizados en la matriz de Telescopio Muy Grande de ESO utilizando un tiempo de exposición total de alrededor de 9 horas |
| +28.4 | asteroides 2003 BH91 | visto desde la órbita terrestre | magnitud observada de Ω15-kilometro Objeto del cinturón de Kuiper visto por el telescopio espacial Hubble (HST) en 2003, más conocido asteroide observado directamente. |
| +31.5 | Objetos más falsos observables en luz visible con Telescopio Espacial Hubble a través del Campo Profundo EXtreme con Ω23 días de exposición recogidos durante 10 años | ||
| +34 | Objetos más falsos observables en luz visible con el telescopio espacial James Webb | ||
| +35 | asteroide sin nombre | visto desde la órbita terrestre | magnitud esperada del asteroide más conocido, un objeto de banda Kuiper de 950 metros descubrió (por el HST) pasando delante de una estrella en 2009. |
| +35 | estrella LBV 1806-20 | visto desde la Tierra | una estrella variable azul luminosa, la magnitud esperada en longitudes de onda visibles debido a la extinción interestelar |
Contenido relacionado
Filosofía del espacio y tiempo
Periodo orbital
Fénix (constelación)

![{displaystyle {sqrt[{5}]{100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d26eff2c044a521107db3cf827e04c2b8415691d)



![{sqrt[{5}]{100}}approx 2.512](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed184113e02b2f8b9edcedca0920c0d14661ead)





