Magnitud absoluta

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Medición de la luminosidad de los objetos celestes

Magnitud absoluta ( $M$ ) es una medida de la luminosidad de un objeto celeste en una escala de magnitud astronómica logarítmica inversa. La magnitud absoluta de un objeto se define como igual a la magnitud aparente que tendría el objeto si fuera visto desde una distancia de exactamente 10 parsecs (32,6 años luz), sin extinción (o atenuación) de su luz debido a la absorción por la materia interestelar y el polvo cósmico. Al colocar hipotéticamente todos los objetos a una distancia de referencia estándar del observador, sus luminosidades se pueden comparar directamente entre sí en una escala de magnitud.

Al igual que con todas las magnitudes astronómicas, la magnitud absoluta se puede especificar para diferentes rangos de longitud de onda correspondientes a bandas de filtro o bandas de paso específicas; para las estrellas, una magnitud absoluta comúnmente citada es la magnitud visual absoluta, que utiliza la banda visual (V) del espectro (en el sistema fotométrico UBV). Las magnitudes absolutas se indican con una M mayúscula, con un subíndice que representa la banda de filtro utilizada para la medición, como M_V para la magnitud absoluta en la banda V.

Cuanto más luminoso es un objeto, menor es el valor numérico de su magnitud absoluta. Una diferencia de 5 magnitudes entre las magnitudes absolutas de dos objetos corresponde a una relación de 100 en sus luminosidades, y una diferencia de n magnitudes en la magnitud absoluta corresponde a una relación de luminosidad de 100^n/5. Por ejemplo, una estrella de magnitud absoluta M_V = 3,0 sería 100 veces más luminosa que una estrella de magnitud absoluta M_V = 8,0 medida en la banda del filtro V. El Sol tiene una magnitud absoluta M_V = +4,83. Los objetos muy luminosos pueden tener magnitudes absolutas negativas: por ejemplo, la Vía Láctea tiene una magnitud B absoluta de aproximadamente −20,8.

La magnitud bolométrica absoluta de un objeto (M_bol) representa su luminosidad total en todas las longitudes de onda, en lugar de en una sola banda de filtro, como se expresa en un escala de magnitud logarítmica. Para convertir una magnitud absoluta en una banda de filtro específica a una magnitud bolométrica absoluta, se aplica una corrección bolométrica (BC).

Para los cuerpos del Sistema Solar que brillan con luz reflejada, se utiliza una definición diferente de magnitud absoluta (H), basada en una distancia de referencia estándar de una unidad astronómica.

Estrellas y galaxias

En astronomía estelar y galáctica, la distancia estándar es de 10 parsecs (alrededor de 32,616 años luz, 308,57 petametros o 308,57 billones de kilómetros). Una estrella a 10 parsecs tiene una paralaje de 0,1″ (100 milisegundos de arco). Las galaxias (y otros objetos extensos) son mucho más grandes que 10 parsecs, su luz se irradia sobre un área extendida del cielo y su brillo general no se puede observar directamente desde distancias relativamente cortas, pero se usa la misma convención. La magnitud de una galaxia se define midiendo toda la luz radiada sobre todo el objeto, tratando ese brillo integrado como el brillo de una sola fuente similar a un punto o similar a una estrella, y calculando la magnitud de esa fuente similar a un punto como aparecería si se observara a la distancia estándar de 10 parsecs. En consecuencia, la magnitud absoluta de cualquier objeto es igual a la magnitud aparente que tendría si estuviera a 10 parsecs de distancia.

Algunas estrellas visibles a simple vista tienen una magnitud absoluta tan baja que parecerían lo suficientemente brillantes como para eclipsar a los planetas y proyectar sombras si estuvieran a 10 parsecs de la Tierra. Los ejemplos incluyen Rigel (-7,0), Deneb (-7,2), Naos (-6,0) y Betelgeuse (-5,6). A modo de comparación, Sirius tiene una magnitud absoluta de solo 1,4, que es aún más brillante que el Sol, cuya magnitud visual absoluta es 4,83. La magnitud bolométrica absoluta del Sol se establece de forma arbitraria, normalmente en 4,75. Las magnitudes absolutas de las estrellas generalmente oscilan entre aproximadamente -10 y +20. Las magnitudes absolutas de las galaxias pueden ser mucho más bajas (más brillantes). Por ejemplo, la galaxia elíptica gigante M87 tiene una magnitud absoluta de −22 (es decir, tan brillante como unas 60 000 estrellas de magnitud −10). Algunos núcleos galácticos activos (quásares como CTA-102) pueden alcanzar magnitudes absolutas superiores a −32, lo que los convierte en los objetos persistentes más luminosos del universo observable, aunque estos objetos pueden variar en brillo en escalas de tiempo astronómicamente cortas. En el extremo, el resplandor óptico residual del estallido de rayos gamma GRB 080319B alcanzó, según un artículo, una magnitud r absoluta más brillante que −38 durante unas pocas decenas de segundos.

Magnitud aparente

El astrónomo griego Hipparchus estableció una escala numérica para describir el brillo de cada estrella que aparece en el cielo. A las estrellas más brillantes del cielo se les asignó una magnitud aparente $m = 1$ , y a las estrellas más tenues visibles a simple vista se les asignó m = 6. La diferencia entre ellos corresponde a un factor de 100 en brillo. Para objetos dentro de la vecindad inmediata del Sol, la magnitud absoluta $M$ y la magnitud aparente $m$ desde cualquier distancia $d$ (en parsecs, con 1 pc = 3,2616 años luz) están relacionados por

{displaystyle 100^{frac {m-M}{5}}={frac {F_{10}}{F}}=left({frac {d}{10;mathrm {pc} }}right)^{2},}

F

d

F 10

10 pc

{displaystyle M=m-5log _{10}(d_{text{pc}})+5=m-5left(log _{10}d_{text{pc}}-1right),}

Para objetos a distancias muy grandes (fuera de la Vía Láctea) la distancia de luminosidad $d L$ (distancia definida usando mediciones de luminosidad) deben usarse en lugar de $d$ , porque la aproximación euclidiana no es válida para objetos distantes. En cambio, se debe tener en cuenta la relatividad general. Además, el corrimiento al rojo cosmológico complica la relación entre la magnitud absoluta y la aparente, porque la radiación observada se desplazó hacia el rango rojo del espectro. Para comparar las magnitudes de objetos muy distantes con las de objetos locales, podría ser necesario aplicar una corrección K a las magnitudes de los objetos distantes.

La magnitud absoluta $M$ también se puede escribir en términos de la magnitud aparente $m$ y paralaje estelar $p$ :

{displaystyle M=m+5left(log _{10}p+1right),}

m

μ

{displaystyle M=m-mu.}

Ejemplos

Rigel tiene una magnitud visual $m V$ de 0,12 y una distancia de unos 860 años luz:

{displaystyle M_{mathrm {V} }=0.12-5left(log _{10}{frac {860}{3.2616}}-1right)=-7.0.}

Vega tiene un paralaje $p$ de 0,129″ y una magnitud aparente $m V$ de 0,03:

{displaystyle M_{mathrm {V} }=0.03+5left(log _{10}{0.129}+1right)=+0.6.}

La Galaxia del Ojo Negro tiene una magnitud visual $m V$ de 9,36 y un módulo de distancia $μ$ de 31.06:

{displaystyle M_{mathrm {V} }=9.36-31.06=-21.7.}

Magnitud bolométrica

La magnitud absoluta bolométrica $M bol$ , tiene en cuenta la radiación electromagnética en todas las longitudes de onda. Incluye los no observados debido a la banda de paso instrumental, la absorción atmosférica de la Tierra y la extinción por el polvo interestelar. Se define en base a la luminosidad de las estrellas. En el caso de estrellas con pocas observaciones, debe calcularse asumiendo una temperatura efectiva.

Clásicamente, la diferencia en la magnitud bolométrica está relacionada con la relación de luminosidad según:

{displaystyle M_{mathrm {bol,star } }-M_{mathrm {bol,odot } }=-2.5log _{10}left({frac {L_{star }}{L_{odot }}}right)}

{displaystyle {frac {L_{star }}{L_{odot }}}=10^{0.4left(M_{mathrm {bol,odot } }-M_{mathrm {bol,star } }right)}}

$L ⊙$ es la luminosidad del Sol (luminosidad bolométrica)
$L ★$ es la luminosidad de la estrella (luminosidad bolométrica)
$M bol,$ es la magnitud bolométrica del Sol
$M Bol,★$ es la magnitud bolométrica de la estrella.

En agosto de 2015, la Unión Astronómica Internacional aprobó la Resolución B2 que define los puntos cero de las escalas de magnitud bolométrica absoluta y aparente en unidades SI para potencia (vatios) e irradiancia (W/m²), respectivamente. Aunque los astrónomos han utilizado magnitudes bolométricas durante muchas décadas, ha habido diferencias sistemáticas en las escalas de luminosidad-magnitud absoluta presentadas en varias referencias astronómicas, y no hay estandarización internacional. Esto condujo a diferencias sistemáticas en las escalas de correcciones bolométricas. Combinado con magnitudes bolométricas absolutas supuestas incorrectas para el Sol, esto podría conducir a errores sistemáticos en las luminosidades estelares estimadas (y otras propiedades estelares, como radios o edades, que dependen de la luminosidad estelar para calcularse).

La resolución B2 define una escala de magnitud bolométrica absoluta donde $M bol = 0$ corresponde a la luminosidad $L 0 = 3.0128 \times 1028 W$ , con la luminosidad del punto cero $L 0$ establecido de tal manera que el Sol (con luminosidad nominal 3,828×10²⁶ W) corresponde a la magnitud bolométrica absoluta $M bol,⊙ = 4,74$ . Colocando una fuente de radiación (por ejemplo, una estrella) a la distancia estándar de 10 parsecs, se deduce que el punto cero de la escala de magnitud bolométrica aparente $m bol = 0$ corresponde a la irradiancia $f 0 = 2.518 021002 \times 10 -8 W/m 2 . Usando la escala IAU 2015, la irradiancia solar total nominal ("constante solar") medida en 1 unidad astronómica (1361 W/m 2) corresponde a una magnitud bolométrica aparente del Sol de m bol,⊙ = -26,832 .$

Después de la Resolución B2, la relación entre la magnitud bolométrica absoluta de una estrella y su luminosidad ya no está directamente relacionada con la luminosidad (variable) del Sol:

{displaystyle M_{mathrm {bol} }=-2.5log _{10}{frac {L_{star }}{L_{0}}}approx -2.5log _{10}L_{star }+71.197425}

$L ★$ es la luminosidad de la estrella (luminosidad bolométrica) en watts
$L 0$ es el punto cero luminosidad 3.0128×10²⁸W
$M perno$ es la magnitud bolométrica de la estrella

La nueva escala de magnitud absoluta de la IAU desconecta permanentemente la escala de la variable Sol. Sin embargo, en esta escala de potencia del SI, la luminosidad solar nominal corresponde estrechamente a $M bol = 4,74$ , valor que fue comúnmente adoptado por los astrónomos antes de la resolución de la IAU de 2015.

La luminosidad de la estrella en vatios se puede calcular en función de su magnitud bolométrica absoluta $M bol$ como:

{displaystyle L_{star }=L_{0}10^{-0.4M_{mathrm {bol} }}}

Cuerpos del Sistema Solar (H)

Abs Mag (H)
y Diámetro
para asteroides
(albedo=0.14)
H	Diámetro
10	36 km
12.7	10 km
15	3,6 km
17,7	1 km
19.2	510 m
20	360 m
22	140 m
22.7	100 m
24.2	51 m
25	36 m
26.6	17 m
27,7	10 m
30	3,6 m
32.7	1 m

Para planetas y asteroides se utiliza una definición de magnitud absoluta más significativa para objetos no estelares. La magnitud absoluta, comúnmente llamada $H$ , se define como la magnitud aparente que el objeto tendría si fuera una unidad astronómica (AU) tanto del Sol como del observador, y en condiciones de oposición solar ideal (un arreglo que es imposible en la práctica). Debido a que los cuerpos del Sistema Solar están iluminados por el Sol, su brillo varía como una función de las condiciones de iluminación, descritas por el ángulo de fase. Esta relación se denomina curva de fase. La magnitud absoluta es el brillo en el ángulo de fase cero, un arreglo conocido como oposición, desde una distancia de una UA.

Magnitud aparente

El ángulo de fase

alpha

se puede calcular a partir de las distancias cuerpo-sun, observador-sun y observador-cuerpo, utilizando la ley de cosines.

La magnitud absoluta $H$ se puede utilizar para calcular la magnitud aparente $m$ de un cuerpo. Para un objeto que refleje la luz solar, $H$ y $m$ están conectados por la relación

{displaystyle m=H+5log _{10}{left({frac {d_{BS}d_{BO}}{d_{0}^{2}}}right)}-2.5log _{10}{q(alpha)},}

alpha

{displaystyle q(alpha)}

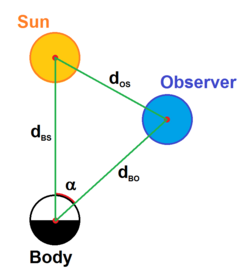
Por la ley de los cosenos, tenemos:

{displaystyle cos {alpha }={frac {d_{mathrm {BO} }^{2}+d_{mathrm {BS} }^{2}-d_{mathrm {OS} }^{2}}{2d_{mathrm {BO} }d_{mathrm {BS} }}}.}

Distancias:

$d BO$ es la distancia entre el cuerpo y el observador
$d BS$ es la distancia entre el cuerpo y el Sol
$d OS$ es la distancia entre el observador y el Sol
$d 0$ , un factor de conversión de unidad, es la constante 1 UA, la distancia promedio entre la Tierra y el Sol

Aproximaciones para la integral de fase q(α)

El valor de ${displaystyle q(alpha)}$ depende de las propiedades de la superficie reflectante, en particular de su rugosidad. En la práctica, se utilizan diferentes aproximaciones basadas en las propiedades conocidas o supuestas de la superficie. Las superficies de los planetas terrestres son generalmente más difíciles de modelar que las de los planetas gaseosos, los cuales tienen superficies visibles más suaves.

Los planetas como esferas difusas

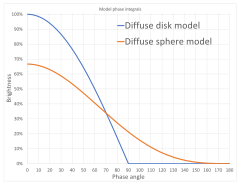
Reflexión difusa en esfera y disco plano

Brillo con fase para modelos de reflexión difusos. La esfera es 2/3 como brillante en fase cero, mientras que el disco no se puede ver más allá de 90 grados.

Los cuerpos planetarios pueden ser aproximados razonablemente así como las esferas de reflexión difundidas ideales. Vamos $alpha$ ser el ángulo de fase en grados, entonces

{displaystyle q(alpha)={frac {2}{3}}left(left(1-{frac {alpha }{180^{circ }}}right)cos {alpha }+{frac {1}{pi }}sin {alpha }right).}

{displaystyle alpha =90^{circ }}

{textstyle {frac {1}{pi }}}

{displaystyle alpha =0^{circ }}

Por contraste, a modelo de reflector de disco difuso es simplemente ${displaystyle q(alpha)=cos {alpha }}$ , que no es realista, pero representa la oleada de oposición para superficies rugosas que reflejan una luz más uniforme en ángulos de baja fase.

La definición del albedo geométrico $p$ , una medida para la reflectividad de las superficies planetarias, se basa en el modelo de reflector de disco difuso. La magnitud absoluta $H$ , diámetro $D$ (en kilómetros) y albedo geométrico $p$ de un cuerpo están relacionados por

{displaystyle D={frac {1329}{sqrt {p}}}times 10^{-0.2H}mathrm {km}.}

Ejemplo: La magnitud absoluta de la Luna $H$ puede calcularse a partir de su diámetro ${displaystyle D=3474{text{ km}}}$ albedo geométrico ${displaystyle p=0.113}$ :

{displaystyle H=5log _{10}{frac {1329}{3474{sqrt {0.113}}}}=+0.28.}

{displaystyle d_{BS}=1{text{ AU}}}

{displaystyle d_{BO}=384400{text{ km}}=0.00257{text{ AU}}.}

{textstyle q(alpha)approx {frac {2}{3pi }}}

{textstyle m=+0.28+5log _{10}{left(1cdot 0.00257right)}-2.5log _{10}{left({frac {2}{3pi }}right)}=-10.99.}

{displaystyle m=-10.0.}

Modelos más avanzados

Debido a que los cuerpos del Sistema Solar nunca son reflectores difusos perfectos, los astrónomos utilizan diferentes modelos para predecir magnitudes aparentes basadas en propiedades conocidas o supuestas del cuerpo. Para planetas, aproximaciones para el plazo de corrección ${displaystyle -2.5log _{10}{q(alpha)}}$ en la fórmula para $m$ han sido derivados empíricamente, para igualar las observaciones en diferentes ángulos de fase. Las aproximaciones recomendadas por el Almanac Astronómico son (con $alpha$ en grados:

Planeta	$H$	Aproximación para ${displaystyle -2.5log _{10}{q(alpha)}}$
Mercurio	−0.613	${displaystyle +6.328times 10^{-2}alpha -1.6336times 10^{-3}alpha ^{2}+3.3644times 10^{-5}alpha ^{3}-3.4265times 10^{-7}alpha ^{4}+1.6893times 10^{-9}alpha ^{5}-3.0334times 10^{-12}alpha ^{6}}$
Venus	−4.384	${displaystyle -1.044times 10^{-3}alpha +3.687times 10^{-4}alpha ^{2}-2.814times 10^{-6}alpha ^{3}+8.938times 10^{-9}alpha ^{4}}$ (por $<math alttext="{displaystyle 0^{circ }0∘ ∘ .α α ≤ ≤ 163.7∘ ∘ {displaystyle 0^{circ }traducidoalpha leq 163.7^{circ }<img alt="{displaystyle 0^{circ }$ ) ${displaystyle +240.44228-2.81914alpha +8.39034times 10^{-3}alpha ^{2}}$ (por $<math alttext="{displaystyle 163.7^{circ }<alpha 163.7∘ ∘ .α α .179∘ ∘ {displaystyle 163.7^{circ }traducidoalpha<img alt="{displaystyle 163.7^{circ }<alpha$ )
Tierra	−3.99	${displaystyle -1.060times 10^{-3}alpha +2.054times 10^{-4}alpha ^{2}}$
Luna	+0.28	${displaystyle +2.9994times 10^{-2}alpha -1.6057times 10^{-4}alpha ^{2}+3.1543times 10^{-6}alpha ^{3}-2.0667times 10^{-8}alpha ^{4}+6.2553times 10^{-11}alpha ^{5}}$ (por ${displaystyle alpha leq 150^{circ }}$ , antes de la Luna Llena ${displaystyle +3.3234times 10^{-2}alpha -3.0725times 10^{-4}alpha ^{2}+6.1575times 10^{-6}alpha ^{3}-4.7723times 10^{-8}alpha ^{4}+1.4681times 10^{-10}alpha ^{5}}$ (por ${displaystyle alpha leq 150^{circ }}$ , después de la Luna Llena
Marte	−1.601	${displaystyle +2.267times 10^{-2}alpha -1.302times 10^{-4}alpha ^{2}}$ (por $<math alttext="{displaystyle 0^{circ }0∘ ∘ .α α ≤ ≤ 50∘ ∘ {displaystyle 0^{circ }traducidoalpha leq 50^{circ }<img alt="{displaystyle 0^{circ }$ ) ${displaystyle +1.234-2.573times 10^{-2}alpha +3.445times 10^{-4}alpha ^{2}}$ (por $<math alttext="{displaystyle 50^{circ }50∘ ∘ .α α ≤ ≤ 120∘ ∘ {displaystyle 50^{circ }traducidoalpha leq 120^{circ }<img alt="{displaystyle 50^{circ }$ )
Júpiter	−9.395	${displaystyle -3.7times 10^{-4}alpha +6.16times 10^{-4}alpha ^{2}}$ (por ${displaystyle alpha leq 12^{circ }}$ ) ${displaystyle -0.033-2.5log _{10}{left(1-1.507left({frac {alpha }{180^{circ }}}right)-0.363left({frac {alpha }{180^{circ }}}right)^{2}-0.062left({frac {alpha }{180^{circ }}}right)^{3}+2.809left({frac {alpha }{180^{circ }}}right)^{4}-1.876left({frac {alpha }{180^{circ }}}right)^{5}right)}}$ (por $12^{circ }}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■12∘ ∘ {displaystyle alpha >{circ }12^{circ }}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e057673768c07c68a13b784b5ee085bccc736f" style="vertical-align: -0.338ex; width:7.965ex; height:2.343ex;"/>$ )
Saturno	−8.914	${displaystyle -1.825sin {left(beta right)}+2.6times 10^{-2}alpha -0.378sin {left(beta right)}e^{-2.25alpha }}$ (para planetas y anillos, $<math alttext="{displaystyle alpha α α .6.5\circ \circ {displaystyle alpha <img alt="{displaystyle alpha$ y $<math alttext="{displaystyle beta β β .27\circ \circ {displaystyle beta } <img alt="{displaystyle beta$ ) ${displaystyle -0.036-3.7times 10^{-4}alpha +6.16times 10^{-4}alpha ^{2}}$ (por el mundo solo, ${displaystyle alpha leq 6^{circ }}$ ) ${displaystyle +0.026+2.446times 10^{-4}alpha +2.672times 10^{-4}alpha ^{2}-1.505times 10^{-6}alpha ^{3}+4.767times 10^{-9}alpha ^{4}}$ (por el mundo solo, $<math alttext="{displaystyle 6^{circ }<alpha 6∘ ∘ .α α .150∘ ∘ {displaystyle 6^{circ }traducidoalpha<img alt="{displaystyle 6^{circ }<alpha$ )
Urano	−7.110	${displaystyle -8.4times 10^{-4}phi '+6.587times 10^{-3}alpha +1.045times 10^{-4}alpha ^{2}}$ (por $<math alttext="{displaystyle alpha α α .3.1\circ \circ {displaystyle alpha <img alt="{displaystyle alpha$ )
Neptuno	7.00	${displaystyle +7.944times 10^{-3}alpha +9.617times 10^{-5}alpha ^{2}}$ (por $<math alttext="{displaystyle alpha α α .133\circ \circ {displaystyle alpha <img alt="{displaystyle alpha$ y $2000.0}" xmlns="http://www.w3.org/1998/Math/MathML">t■2000.0{displaystyle t fiel2000.0}2000.0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f7c88b73a26963516110c9f7ef7029a222105bc5" style="vertical-align: -0.338ex; width:10.397ex; height:2.176ex;"/>$ )

Las diferentes mitades de la Luna, como se ve desde la Tierra

Luna al primer trimestre

Luna en el último trimestre

Aquí. $beta$ es la inclinación efectiva de los anillos de Saturno (su inclinación relativa al observador), que como se ve desde la Tierra varía entre 0° y 27° sobre el curso de una órbita de Saturno, y $phi '$ es un pequeño plazo de corrección dependiendo de las latitudes sub-Tierra y subsolar de Urano. $t$ es el año de la Era Común. La magnitud absoluta de Neptuno está cambiando lentamente debido a los efectos estacionales a medida que el planeta se mueve a lo largo de su órbita de 165 años alrededor del Sol, y la aproximación anterior sólo es válida después del año 2000. Por algunas circunstancias, como ${displaystyle alpha geq 179^{circ }}$ para Venus, no hay observaciones disponibles, y la curva de fase es desconocida en esos casos. La fórmula para la Luna sólo es aplicable al lado cercano de la Luna, la porción que es visible desde la Tierra.

Ejemplo 1: El 1 de enero de 2019, Venus fue ${displaystyle d_{BS}=0.719{text{ AU}}}$ del Sol, y ${displaystyle d_{BO}=0.645{text{ AU}}}$ desde la Tierra, en un ángulo de fase ${displaystyle alpha =93.0^{circ }}$ (near cuarta fase). Bajo condiciones de plena fase, Venus habría sido visible en ${displaystyle m=-4.384+5log _{10}{left(0.719cdot 0.645right)}=-6.09.}$ Contabilidad para el ángulo de alta fase, el plazo de corrección anterior produce una magnitud aparente real ${displaystyle m=-6.09+left(-1.044times 10^{-3}cdot 93.0+3.687times 10^{-4}cdot 93.0^{2}-2.814times 10^{-6}cdot 93.0^{3}+8.938times 10^{-9}cdot 93.0^{4}right)=-4.59.}$ Esto está cerca del valor ${displaystyle m=-4.62}$ predicho por el Laboratorio de Propulsión Jet.

Ejemplo 2: En la primera fase, la aproximación para la Luna da ${textstyle -2.5log _{10}{q(90^{circ })}=2.71.}$ Con eso, la aparente magnitud de la Luna es ${textstyle m=+0.28+5log _{10}{left(1cdot 0.00257right)}+2.71=-9.96,}$ cerca del valor esperado de aproximadamente ${displaystyle -10.0}$ . En el último trimestre, la Luna es aproximadamente 0.06 mag más débil que en el primer trimestre, porque esa parte de su superficie tiene un albedo inferior.

El albedo de la Tierra varía por un factor de 6, de 0,12 en el caso sin nubes a 0,76 en el caso de nubes altoestratos. La magnitud absoluta en la tabla corresponde a un albedo de 0,434. Debido a la variabilidad del clima, la magnitud aparente de la Tierra no se puede predecir con tanta precisión como la de la mayoría de los otros planetas.

Asteroides

Asteroid 1 Ceres, representado por la nave espacial Dawn en ángulos de fase de 0°, 7° y 33°. La fuerte diferencia en el brillo entre los tres es real. La imagen izquierda en ángulo de fase 0° muestra el aumento del brillo debido al efecto de oposición.

Integrantes de fase para diversos valores de G

Relación entre el parámetro de pendiente

G

y el aumento de la oposición. Valores más grandes de

G

corresponde a un efecto de oposición menos pronunciado. Para la mayoría de los asteroides, un valor de

{displaystyle G=0.15}

se asume, correspondiente a una oleada de oposición

{displaystyle 0.3{text{ mag}}}

Si un objeto tiene una atmósfera, refleja la luz más o menos isotropicamente en todas las direcciones, y su brillo puede ser modelado como un reflector difuso. Los cuerpos sin atmósfera, como asteroides o lunas, tienden a reflejar la luz más fuertemente a la dirección de la luz del incidente, y su brillo aumenta rápidamente a medida que el ángulo de fase se acerca ${displaystyle 0^{circ }}$ . Este rápido resplandor cerca de la oposición se llama efecto de oposición. Su fuerza depende de las propiedades físicas de la superficie del cuerpo, y por lo tanto difiere de asteroides a asteroides.

En 1985, la OUA adoptó la semiempírica $HG$ -sistema, basado en dos parámetros $H$ y $G$ llamado magnitud absoluta y pendiente, para modelar el efecto de oposición para los efímeros publicados por el Centro del Planeta Menor.

{displaystyle m=H+5log _{10}{left({frac {d_{BS}d_{BO}}{d_{0}^{2}}}right)}-2.5log _{10}{q(alpha)},}

dónde

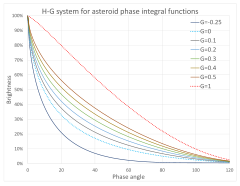
la fase integral es ${displaystyle q(alpha)=left(1-Gright)phi _{1}left(alpha right)+Gphi _{2}left(alpha right)}$ y
${textstyle phi _{i}left(alpha right)=exp {left(-A_{i}left(tan {frac {alpha }{2}}right)^{B_{i}}right)}}$ para $i=1$ o $2$ , ${displaystyle A_{1}=3.332}$ , ${displaystyle A_{2}=1.862}$ , ${displaystyle B_{1}=0.631}$ y ${displaystyle B_{2}=1.218}$ .

Esta relación es válida para ángulos de fase $<math alttext="{displaystyle alpha α α .120\circ \circ {displaystyle alpha <img alt="{displaystyle alpha$ , y funciona mejor cuando $<math alttext="{displaystyle alpha α α .20\circ \circ {displaystyle alpha <img alt="{displaystyle alpha$ .

El parámetro de pendiente $G$ se relaciona con el aumento del brillo, típicamente 0.3 mag, cuando el objeto está cerca de la oposición. Se conoce exactamente sólo para un pequeño número de asteroides, por lo tanto para la mayoría de asteroides un valor de ${displaystyle G=0.15}$ es asumido. En casos raros, $G$ puede ser negativo. Un ejemplo es 101955 Bennu, con ${displaystyle G=-0.08}$ .

En 2012, el $HG$ - El sistema fue reemplazado oficialmente por un sistema mejorado con tres parámetros $H$ , $G_{1}$ y $G_{2}$ , que produce resultados más satisfactorios si el efecto de oposición es muy pequeño o restringido a ángulos de fase muy pequeños. Sin embargo, a partir de 2022, esto ${displaystyle HG_{1}G_{2}}$ - El sistema no ha sido adoptado por el Centro de Planetas Menores ni el Laboratorio de Propulsión Jet.

La aparente magnitud de los asteroides varía cuando giran, a escalas de tiempo de segundos a semanas dependiendo de su período de rotación, hasta ${displaystyle 2{text{ mag}}}$ o más. Además, su magnitud absoluta puede variar con la dirección de visualización, dependiendo de su inclinación axial. En muchos casos, ni se conoce el período de rotación ni la inclinación axial, limitando la previsibilidad. Los modelos presentados aquí no capturan esos efectos.

Magnitudes cometarias

El brillo de los cometas se da por separado como total () $m_{{1}}$ , el brillo integrado sobre toda la extensión visible del coma) y magnitud nuclear () $m_{{2}}$ , el brillo de la región central sola). Ambas son diferentes escalas que la escala de magnitud utilizada para planetas y asteroides, y no se puede utilizar para una comparación de tamaño con la magnitud absoluta de un asteroide $H$ .

La actividad de los cometas varía con su distancia al Sol. Su brillo se puede aproximar como

{displaystyle m_{1}=M_{1}+2.5cdot K_{1}log _{10}{left({frac {d_{BS}}{d_{0}}}right)}+5log _{10}{left({frac {d_{BO}}{d_{0}}}right)}}

{displaystyle m_{2}=M_{2}+2.5cdot K_{2}log _{10}{left({frac {d_{BS}}{d_{0}}}right)}+5log _{10}{left({frac {d_{BO}}{d_{0}}}right)},}

{displaystyle m_{1,2}}

{displaystyle M_{1,2}}

{displaystyle d_{BS}}

{displaystyle d_{BO}}

{displaystyle d_{0}}

{displaystyle K_{1,2}}

K=2

Por ejemplo, el faro del cometa C/2011 L4 (PANSTARRS) puede ser aproximado por ${displaystyle M_{1}=5.41{text{, }}K_{1}=3.69.}$ El día de su pasaje perihelio, 10 de marzo de 2013, el cometa PANSTARRS fue ${displaystyle 0.302{text{ AU}}}$ del Sol y ${displaystyle 1.109{text{ AU}}}$ de la Tierra. La magnitud total aparente $m_{{1}}$ se predijo que ${displaystyle m_{1}=5.41+2.5cdot 3.69cdot log _{10}{left(0.302right)}+5log _{10}{left(1.109right)}=+0.8}$ en ese momento. El Centro Planetario Menor da un valor cercano a eso, ${displaystyle m_{1}=+0.5}$ .

Alcances y tamaños absolutos de núcleos de cometa
Comet	Absoluto magnitud $M_{{1}}$	Nucleus diámetro
Comet Sarabat	−3.0	¿A 100 km?
Comet Hale-Bopp	−1.3	60 ± 20 km
Comet Halley	4.0	14.9 x 8,2 km
promedio nuevo cometa	6.5	■2 km
C/2014 UN271 (Bernardinelli-Bernstein)	6.7	¿60 a 200 km?
289P/Blanpain (durante el desembolso de 1819)	8,5	320 m
289P/Blanpaina (actividad normal)	22.9	320 m

La magnitud absoluta de cualquier cometa puede variar dramáticamente. Puede cambiar a medida que el cometa se vuelve más o menos activo con el tiempo o si sufre un desembolso. Esto hace difícil utilizar la magnitud absoluta para una estimación de tamaño. Cuando el cometa 289P/Blanpain fue descubierto en 1819, se estimó su magnitud absoluta ${displaystyle M_{1}=8.5}$ . Posteriormente se perdió y sólo se redescubrió en 2003. En ese momento, su magnitud absoluta había disminuido a ${displaystyle M_{1}=22.9}$ , y se dio cuenta de que la aparición de 1819 coincidió con un desembolso. 289P/Blanpain alcanzó el brillo de ojos desnudos (5-8 mag) en 1819, aunque es el cometa con el núcleo más pequeño que se ha caracterizado físicamente, y por lo general no se vuelve más brillante que 18 mag.

Para algunos cometas que se han observado a distancias heliocéntricas lo suficientemente grandes como para distinguir entre la luz reflejada desde la coma y la luz del propio núcleo, se ha calculado una magnitud absoluta análoga a la utilizada para los asteroides, lo que permite estimar los tamaños de sus núcleos.

Meteoritos

Para un meteoro, la distancia estándar para la medición de magnitudes es a una altitud de 100 km (62 mi) en el cenit del observador.

Contenido relacionado

Más resultados...