Magnetohidrodinámica
Magnetohidrodinámica (MHD; también llamada magnetodinámica de fluidos o hidromagnetismo) es el estudio de la propiedades y comportamiento de los fluidos conductores de electricidad. Los ejemplos de tales magnetofluidos incluyen plasmas, metales líquidos, agua salada y electrolitos. La palabra magnetohidrodinámica se deriva de magneto- que significa campo magnético, hidro - que significa agua, y dinámica que significa movimiento. El campo de MHD fue iniciado por Hannes Alfvén, por lo que recibió el Premio Nobel de Física en 1970.
El concepto fundamental detrás de MHD es que los campos magnéticos pueden inducir corrientes en un fluido conductor en movimiento, que a su vez polariza el fluido y cambia recíprocamente el propio campo magnético. El conjunto de ecuaciones que describen MHD son una combinación de las ecuaciones de dinámica de fluidos de Navier-Stokes y las ecuaciones de electromagnetismo de Maxwell. Estas ecuaciones diferenciales deben resolverse simultáneamente, ya sea analítica o numéricamente.
Historia
El primer uso registrado de la palabra magnetohidrodinámica es de Hannes Alfvén en 1942:
Por fin se hacen algunas observaciones sobre la transferencia del impulso del Sol a los planetas, que es fundamental para la teoría. Se señala la importancia de las ondas Magnetohidrodinámicas a este respecto.
El agua salada menguante que pasa por el puente Waterloo de Londres interactúa con el campo magnético de la Tierra para producir una diferencia de potencial entre las dos orillas del río. Michael Faraday llamó a este efecto "inducción magnetoeléctrica" e intentó este experimento en 1832, pero la corriente era demasiado pequeña para medirla con el equipo en ese momento, y el lecho del río contribuyó a provocar un cortocircuito en la señal. Sin embargo, mediante un proceso similar, en 1851 se midió el voltaje inducido por la marea en el Canal de la Mancha.
Faraday omitió cuidadosamente el término hidrodinámica en este trabajo. Por omisión, se ha excluido todo un cuerpo de trabajo sobre la energía hidromagnética dentro de las represas.
MHD ideal y resistiva
(feminine)La forma más simple de MHD, Ideal MHD, asume que el fluido tiene tan poca resistividad que puede tratarse como un conductor perfecto. Este es el límite del número de Reynolds magnético infinito. En MHD ideal, la ley de Lenz dicta que el fluido está, en cierto sentido, ligado a las líneas del campo magnético. Para explicarlo, en el MHD ideal, un pequeño volumen de fluido similar a una cuerda que rodea una línea de campo continuará a lo largo de una línea de campo magnético, incluso cuando esté torcido y distorsionado por los flujos de fluido en el sistema. Esto a veces se denomina líneas de campo magnético "congeladas" en el fluido La conexión entre las líneas de campo magnético y el fluido en MHD ideal fija la topología del campo magnético en el fluido; por ejemplo, si un conjunto de líneas de campo magnético se atan en un nudo, permanecerán así mientras el fluido/plasma tiene una resistividad despreciable. Esta dificultad para volver a conectar las líneas del campo magnético permite almacenar energía moviendo el fluido o la fuente del campo magnético. Luego, la energía puede estar disponible si las condiciones para un MHD ideal se rompen, lo que permite una reconexión magnética que libera la energía almacenada del campo magnético.
Ecuaciones MHD ideales
Las ecuaciones ideales de MHD constan de la ecuación de continuidad, la ecuación del momento de Cauchy, la ley de Ampere sin tener en cuenta la corriente de desplazamiento y una ecuación de evolución de la temperatura. Al igual que con cualquier descripción de fluidos de un sistema cinético, se debe aplicar una aproximación de cierre al momento más alto de la ecuación de distribución de partículas. Esto a menudo se logra con aproximaciones al flujo de calor a través de una condición de adiabaticidad o isotermalidad.
Las principales cantidades que caracterizan al fluido conductor de electricidad son el campo de velocidad de plasma a granel v, la densidad de corriente J, la densidad de masa ρ y la presión del plasma p. La carga eléctrica que fluye en el plasma es la fuente de un campo magnético B y un campo eléctrico E. Todas las cantidades generalmente varían con el tiempo t. Se usará la notación de operadores vectoriales, en particular ∇ es gradiente, ∇ ⋅ es divergencia y ∇ × es curl.
La ecuación de continuidad de masa es
- ∂ ∂ *** *** ∂ ∂ t+Silencio Silencio ⋅ ⋅ ()*** *** v)=0.{displaystyle {frac {partial rho }{partial t}}+nabla cdot left(rho mathbf {v} right)=0.}
La ecuación del momento de Cauchy es
- *** *** ()∂ ∂ ∂ ∂ t+v⋅ ⋅ Silencio Silencio )v=J× × B− − Silencio Silencio p.{displaystyle rho left({frac {partial }{partial t}+mathbf {v} cdot nabla right)mathbf {v} =mathbf {J} times mathbf {B} -nabla p.}
El término de fuerza de Lorentz J × B se puede expandir usando la ley de Ampère y el cálculo vectorial identidad
- 12Silencio Silencio ()B⋅ ⋅ B)=()B⋅ ⋅ Silencio Silencio )B+B× × ()Silencio Silencio × × B){displaystyle {tfrac {1}{2}nabla (mathbf {B} cdot mathbf {B})=(mathbf {B} cdot nabla)mathbf {B} +mathbf {B} times (nabla times mathbf {B}}})}
dar
- J× × B=()B⋅ ⋅ Silencio Silencio )Bμ μ 0− − Silencio Silencio ()B22μ μ 0),{displaystyle mathbf {J} times mathbf {B} ={frac {left(mathbf {B} cdot nabla right)mathbf {B}{mu} ¿Qué? {B^{2}{2mu _{0}}derecha),}
donde el primer término del lado derecho es la fuerza de tensión magnética y el segundo término es la fuerza de presión magnética.
La ley de Ohm ideal para un plasma viene dada por
- E+v× × B=0.{displaystyle mathbf {E} +mathbf {v} times mathbf {B} =0.}
La ley de Faraday es
- ∂ ∂ B∂ ∂ t=− − Silencio Silencio × × E.{displaystyle {frac {partial mathbf {B}{partial t}=-nabla times mathbf {E}
La ley de Ampère de baja frecuencia desprecia la corriente de desplazamiento y viene dada por
- μ μ 0J=Silencio Silencio × × B.{displaystyle mu _{0}mathbf {J} =nabla times mathbf {B}
La restricción de divergencia magnética es
- Silencio Silencio ⋅ ⋅ B=0.{displaystyle nabla cdot mathbf {B} =0.}
La ecuación de la energía está dada por
- ddt()p*** *** γ γ )=0,{displaystyle {frac {mathrm}{mathrm {} t}left({frac {}{rho }{gamma - Sí.
donde γ = 5/3 es la proporción de calores específicos para una ecuación de estado adiabática. Esta ecuación de energía solo es aplicable en ausencia de choques o conducción de calor, ya que supone que la entropía de un elemento fluido no cambia.
Aplicabilidad de MHD ideal a plasmas
El MHD ideal solo es estrictamente aplicable cuando:
- El plasma es fuertemente colisional, por lo que la escala de tiempo de las colisiones es más corta que los otros tiempos característicos del sistema, y las distribuciones de partículas están por lo tanto cerca de Maxwellian.
- La resistencia debido a estas colisiones es pequeña. En particular, los tiempos típicos de difusión magnética sobre cualquier longitud de escala presente en el sistema deben ser más largos que cualquier escala de tiempo de interés.
- Interés en escalas de longitud mucho más largas que la profundidad de la piel de iones y Larmor radius perpendicular al campo, lo suficientemente largo a lo largo del campo para ignorar el humedecimiento de Landau, y escalas de tiempo mucho más largo que el tiempo de hidratación de iones (sistema es suave y evoluciona lentamente).
Importancia de la resistividad
En un fluido conductor imperfecto, el campo magnético generalmente puede moverse a través del fluido siguiendo una ley de difusión con la resistividad del plasma sirviendo como constante de difusión. Esto significa que las soluciones de las ecuaciones MHD ideales solo son aplicables durante un tiempo limitado para una región de un tamaño determinado antes de que la difusión se vuelva demasiado importante como para ignorarla. Se puede estimar que el tiempo de difusión a través de una región solar activa (a partir de la resistividad de colisión) es de cientos a miles de años, mucho más que el tiempo de vida real de una mancha solar, por lo que parecería razonable ignorar la resistividad. Por el contrario, un volumen de agua de mar del tamaño de un metro tiene un tiempo de difusión magnética medido en milisegundos.
Incluso en los sistemas físicos, que son lo suficientemente grandes y conductivos como para que las estimaciones simples del número de Lundquist sugieran que se puede ignorar la resistividad, la resistividad aún puede ser importante: existen muchas inestabilidades que pueden aumentar la resistividad efectiva del plasma por factores de más de 109. La resistividad mejorada suele ser el resultado de la formación de estructuras a pequeña escala, como láminas de corriente o turbulencias magnéticas a pequeña escala, que introducen pequeñas escalas espaciales en el sistema sobre las que se rompe el MHD ideal y la difusión magnética puede ocurrir rápidamente. Cuando esto sucede, puede ocurrir una reconexión magnética en el plasma para liberar la energía magnética almacenada en forma de ondas, aceleración mecánica masiva del material, aceleración de partículas y calor.
La reconexión magnética en sistemas altamente conductivos es importante porque concentra la energía en el tiempo y el espacio, de modo que las fuerzas suaves aplicadas a un plasma durante largos períodos de tiempo pueden causar explosiones violentas y ráfagas de radiación.
Cuando el fluido no puede considerarse completamente conductivo, pero se cumplen las demás condiciones para un MHD ideal, es posible utilizar un modelo extendido denominado MHD resistivo. Esto incluye un término adicional en la Ley de Ohm que modela la resistividad de colisión. En general, las simulaciones por computadora MHD son al menos algo resistivas porque su cuadrícula computacional introduce una resistividad numérica.
Importancia de los efectos cinéticos
Otra limitación de MHD (y de las teorías de fluidos en general) es que dependen de la suposición de que el plasma es fuertemente colisivo (este es el primer criterio mencionado anteriormente), por lo que la escala de tiempo de las colisiones es más corta que la otra característica. tiempos en el sistema, y las distribuciones de partículas son maxwellianas. Este no suele ser el caso en los plasmas de fusión, espaciales y astrofísicos. Cuando este no es el caso, o el interés está en escalas espaciales más pequeñas, puede ser necesario utilizar un modelo cinético que represente adecuadamente la forma no maxwelliana de la función de distribución. Sin embargo, debido a que MHD es relativamente simple y captura muchas de las propiedades importantes de la dinámica del plasma, a menudo es cualitativamente preciso y, por lo tanto, a menudo es el primer modelo probado.
Los efectos que son esencialmente cinéticos y no captados por los modelos de fluidos incluyen capas dobles, amortiguamiento de Landau, una amplia gama de inestabilidades, separación química en plasmas espaciales y fuga de electrones. En el caso de las interacciones láser de ultra alta intensidad, las escalas de tiempo increíblemente cortas de la deposición de energía significan que los códigos hidrodinámicos no logran capturar la física esencial.
Estructuras en sistemas MHD
En muchos sistemas MHD, la mayor parte de la corriente eléctrica se comprime en cintas delgadas casi bidimensionales denominadas láminas de corriente. Estos pueden dividir el fluido en dominios magnéticos, dentro de los cuales las corrientes son relativamente débiles. Hojas actuales en Se cree que la corona solar tiene entre unos pocos metros y unos pocos kilómetros de espesor, que es bastante delgada en comparación con los dominios magnéticos (que tienen miles o cientos de miles de kilómetros de ancho). Otro ejemplo está en la magnetosfera de la Tierra, donde las láminas de corriente separan dominios topológicamente distintos, aislando la mayor parte de la ionosfera de la Tierra del viento solar.
Olas
Los modos de onda derivados de la teoría del plasma MHD se denominan ondas magnetohidrodinámicas u ondas MHD. En general, hay tres modos de onda MHD:
- Puro (o oblicuo) onda Alfvén
- onda MHD lenta
- Onda rápida MHD
Todas estas ondas tienen velocidades de fase constantes para todas las frecuencias y, por lo tanto, no hay dispersión. En los límites cuando el ángulo entre el vector de propagación de ondas k y el campo magnético B es 0° (180°) o 90°, los modos de onda se denominan:
| Nombre | Tipo | Propagación | Velocidad de fase | Association | Mediana | Otros nombres |
|---|---|---|---|---|---|---|
| Ola de sonido | longitudinal | k ∥ B | velocidad adiabática del sonido | ninguno | líquido compresible, no conductor | |
| Alfvén wave | transversal | k ∥ B | Velocidad de Alfvén | B | onda Alfvén, onda Alfvén lenta, onda torsional Alfvén | |
| Ola Magnetosónica | longitudinal | k ⟂ B | B, E | compresión onda Alfvén, onda Alfvén rápida, onda magnetoacústica |
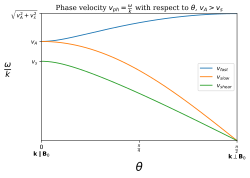
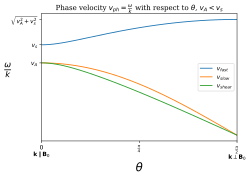
La velocidad de fase depende del ángulo entre el vector de onda k y el campo magnético B . Una onda MHD que se propaga en un ángulo arbitrario θ con respecto al campo volumétrico o independiente del tiempo B0 satisfará la relación de dispersión
- ⋅ ⋅ k=vA# Silencio Silencio {displaystyle {frac {omega } {k}=v_{A}cos theta }
dónde
- vA=B0μ μ 0*** *** {displaystyle v_{A}={frac {B_{0}{sqrt {m}}}} {cH0}} {cH0}}} {cH0}}}} {cH0}}}}} {cH0}}}}}}} {cH}}}}}} {cH}}}} {cH0}}}}}}}}}}} {\ccH}}}}}}}}}}}}}}}}}}}}}}}}}}}} {ccccccccccccccccccccccH}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
es la velocidad de Alfvén. Esta rama corresponde al modo cortante de Alfvén. Además, la ecuación de dispersión da
- ⋅ ⋅ k=()12()vA2+vs2)± ± 12()vA2+vs2)2− − 4vs2vA2#2 Silencio Silencio )12{displaystyle {frac {omega }=left({tfrac {1}{2}left (v_{A}{2}+v_{2}right)pm {tfrac {1}{2}{sqrt {left] ¿Qué? {1}{2}}}
dónde
- vs=γ γ p*** *** {displaystyle {fnK} {fnMic {cH00} {fnMicrosoft} {fnMicrosoft Sans}} {f}fnK} }
es la velocidad del sonido del gas ideal. La rama positiva corresponde al modo de onda MHD rápido y la rama negativa corresponde al modo de onda MHD lento.
Las oscilaciones MHD se amortiguarán si el fluido no es perfectamente conductor pero tiene una conductividad finita, o si hay efectos viscosos.
Las ondas y oscilaciones MHD son una herramienta popular para el diagnóstico remoto de plasmas astrofísicos y de laboratorio, por ejemplo, la corona del Sol (sismología coronal).
Extensiones
- Resistive
- MHD resistivo describe fluidos magnetizados con difusividad de electrones finitos (. ل 0). Esta difusividad conduce a una ruptura en la topología magnética; las líneas de campo magnético pueden 'reconectarse' cuando chocan. Normalmente este término es pequeño y las reconexiones se pueden manejar pensando en ellos como no disimilares a los choques; este proceso ha demostrado ser importante en las interacciones magnéticas de la Tierra-Solar.
- Extended
- MHD extendido describe una clase de fenómenos en plasmas que son más altos que el MHD resistivo, pero que pueden tratarse adecuadamente con una sola descripción del fluido. Estos incluyen los efectos de la física Hall, gradientes de presión de electrones, Larmor Radii finito en el giromo de partículas, e inercia de electrones.
- Dos fluidos
- MHD de dos fluidos describe plasmas que incluyen un campo eléctrico Hall no insignificante. Como resultado, el electron y ion momenta deben ser tratados por separado. Esta descripción está más estrechamente ligada a las ecuaciones de Maxwell como una ecuación de evolución para el campo eléctrico existe.
- Hall
- En 1960, M. J. Lighthill criticó la aplicabilidad de la teoría ideal o resistiva del MHD para plasmas. Se refería al abandono del "Hall current term", una simplificación frecuente hecha en la teoría de la fusión magnética. Hall-magnetohidrodinámica (HMHD) tiene en cuenta esta descripción de campo eléctrico de magnetohidrodinámica. La diferencia más importante es que en ausencia de ruptura de la línea de campo, el campo magnético está ligado a los electrones y no al líquido de vracs.
- Electron MHD
- Electron Magnetohidrodinámica (EMHD) describe plasmas de pequeñas escalas cuando el movimiento de electrones es mucho más rápido que el ion uno. Los principales efectos son los cambios en las leyes de conservación, la resistencia adicional, la importancia de la inercia electrones. Muchos efectos de Electron MHD son similares a los efectos de los dos fluidos MHD y el Hall MHD. EMHD es especialmente importante para los interruptores de z-pinch, reconexión magnética, propulsores de iones, estrellas de neutrones y plasma.
- Sin colisión
- MHD también se utiliza a menudo para plasmas sin colisión. En ese caso las ecuaciones MHD se derivan de la ecuación Vlasov.
- Reducción
- Mediante un análisis multiescala las ecuaciones (resistivas) MHD pueden reducirse a un conjunto de cuatro ecuaciones de escalar cerradas. Esto permite, entre otras cosas, cálculos numéricos más eficientes.
Aplicaciones
Geofísica
Debajo del manto de la Tierra se encuentra el núcleo, que se compone de dos partes: el núcleo interno sólido y el núcleo externo líquido. Ambos tienen cantidades significativas de hierro. El núcleo exterior líquido se mueve en presencia del campo magnético y se forman remolinos en el mismo debido al efecto Coriolis. Estos remolinos desarrollan un campo magnético que aumenta el campo magnético original de la Tierra, un proceso que es autosuficiente y se llama dínamo geomagnético.
Basándose en las ecuaciones MHD, Glatzmaier y Paul Roberts han creado un modelo de supercomputadora del interior de la Tierra. Después de ejecutar las simulaciones durante miles de años en tiempo virtual, se pueden estudiar los cambios en el campo magnético de la Tierra. Los resultados de la simulación concuerdan bien con las observaciones, ya que las simulaciones predijeron correctamente que el campo magnético de la Tierra cambia cada pocos cientos de miles de años. Durante los giros, el campo magnético no desaparece por completo, simplemente se vuelve más complejo.
Terremotos
Algunas estaciones de monitoreo han informado que los terremotos a veces están precedidos por un pico en la actividad de frecuencia ultra baja (ULF). Un ejemplo notable de esto ocurrió antes del terremoto de Loma Prieta en California en 1989, aunque un estudio posterior indica que esto fue poco más que un mal funcionamiento del sensor. El 9 de diciembre de 2010, los geocientíficos anunciaron que el satélite DEMETER observó un aumento espectacular de las ondas de radio ULF sobre Haití en el mes anterior al terremoto de magnitud 7,0 Mw de 2010. Los investigadores están tratando de aprender más sobre esta correlación para averiguar si este método se puede utilizar como parte de un sistema de alerta temprana para terremotos.
Astrofísica
MHD se aplica a la astrofísica, incluidas las estrellas, el medio interplanetario (espacio entre los planetas) y posiblemente dentro del medio interestelar (espacio entre las estrellas) y chorros. La mayoría de los sistemas astrofísicos no están en equilibrio térmico local y, por lo tanto, requieren un tratamiento cinemático adicional para describir todos los fenómenos dentro del sistema (ver Plasma astrofísico).
Las manchas solares son causadas por los campos magnéticos del Sol, como teorizó Joseph Larmor en 1919. El viento solar también se rige por MHD. La rotación solar diferencial puede ser el efecto a largo plazo del arrastre magnético en los polos del Sol, un fenómeno MHD debido a la forma de espiral de Parker asumida por el campo magnético extendido del Sol.
Anteriormente, las teorías que describían la formación del Sol y los planetas no podían explicar cómo el Sol tiene el 99,87 % de la masa, pero solo el 0,54 % del momento angular en el Sistema Solar. En un sistema cerrado como la nube de gas y polvo a partir de la cual se formó el Sol, la masa y el momento angular se conservan. Esa conservación implicaría que a medida que la masa se concentrara en el centro de la nube para formar el Sol, giraría más rápido, como un patinador que tira de sus brazos. La alta velocidad de rotación predicha por las primeras teorías habría arrojado al proto-Sol. aparte antes de que pudiera haberse formado. Sin embargo, los efectos magnetohidrodinámicos transfieren el momento angular del Sol al sistema solar exterior, lo que ralentiza su rotación.
Se sabe que la ruptura del MHD ideal (en forma de reconexión magnética) es la causa probable de las erupciones solares. El campo magnético en una región solar activa sobre una mancha solar puede almacenar energía que se libera repentinamente como un estallido de movimiento, rayos X y radiación cuando la lámina de corriente principal colapsa, reconectando el campo.
Sensores
Los sensores magnetohidrodinámicos se utilizan para mediciones de precisión de velocidades angulares en sistemas de navegación inercial, como en la ingeniería aeroespacial. La precisión mejora con el tamaño del sensor. El sensor es capaz de sobrevivir en entornos hostiles.
Ingeniería
MHD está relacionado con problemas de ingeniería como el confinamiento de plasma, el enfriamiento de metal líquido de reactores nucleares y la fundición electromagnética (entre otros).
Un impulso magnetohidrodinámico o propulsor MHD es un método para propulsar embarcaciones marítimas utilizando solo campos eléctricos y magnéticos sin partes móviles, usando magnetohidrodinámica. El principio de funcionamiento implica la electrificación del propulsor (gas o agua) que luego puede ser dirigido por un campo magnético, empujando el vehículo en la dirección opuesta. Aunque existen algunos prototipos que funcionan, las unidades MHD siguen siendo poco prácticas.
El primer prototipo de este tipo de propulsión fue construido y probado en 1965 por Steward Way, profesor de ingeniería mecánica en la Universidad de California, Santa Bárbara. Way, en una licencia de su trabajo en Westinghouse Electric, asignó a sus estudiantes universitarios de último año a desarrollar un submarino con este nuevo sistema de propulsión. A principios de la década de 1990, una fundación en Japón (Ship & Ocean Foundation (Minato-ku, Tokio)) construyó un barco experimental, el Yamato-1, que utilizaba un accionamiento magnetohidrodinámico que incorporaba un superconductor enfriado por helio líquido, y podía viajar a 15 km/h.
La generación de energía MHD alimentada por gas de combustión de carbón sembrado de potasio mostró potencial para una conversión de energía más eficiente (la ausencia de partes móviles sólidas permite la operación a temperaturas más altas), pero fracasó debido a dificultades técnicas de costo prohibitivo. Un problema de ingeniería importante fue la falla de la pared de la cámara de combustión de carbón primario debido a la abrasión.
En microfluídica, MHD se estudia como una bomba de fluido para producir un flujo continuo y no pulsante en un diseño de microcanal complejo.
MHD se puede implementar en el proceso de colada continua de metales para suprimir inestabilidades y controlar el flujo.
Los problemas MHD industriales se pueden modelar utilizando el software de código abierto EOF-Library. Dos ejemplos de simulación son 3D MHD con una superficie libre para la fusión por levitación electromagnética y agitación de metal líquido mediante la rotación de imanes permanentes.
Dirección de fármacos magnéticos
Una tarea importante en la investigación del cáncer es desarrollar métodos más precisos para administrar medicamentos en las áreas afectadas. Un método implica la unión del medicamento a partículas magnéticas biológicamente compatibles (como los ferrofluidos), que se guían hacia el objetivo mediante la colocación cuidadosa de imanes permanentes en el cuerpo externo. Las ecuaciones magnetohidrodinámicas y el análisis de elementos finitos se utilizan para estudiar la interacción entre las partículas de fluido magnético en el torrente sanguíneo y el campo magnético externo.
Contenido relacionado
Movimiento retrógrado aparente
Cronología de la agricultura y la tecnología alimentaria
Lev Landau