Longitud focal

El punto focal F y longitud focal f de una lente positiva (convex), una lente negativa (concave), un espejo concave y un espejo convexo.

La distancia focal de un sistema óptico es una medida de la fuerza con la que el sistema converge o diverge la luz; es la inversa de la potencia óptica del sistema. Una distancia focal positiva indica que un sistema converge en luz, mientras que una distancia focal negativa indica que el sistema diverge en luz. Un sistema con una distancia focal más corta desvía los rayos más bruscamente, enfocándolos en una distancia más corta o divergiéndolos más rápidamente. Para el caso especial de una lente delgada en el aire, una distancia focal positiva es la distancia sobre la cual los rayos inicialmente colimados (paralelos) se enfocan, o alternativamente, una distancia focal negativa indica qué tan lejos en frente de la lente debe estar una fuente puntual. ubicarse para formar un haz colimado. Para sistemas ópticos más generales, la distancia focal no tiene un significado intuitivo; es simplemente la inversa de la potencia óptica del sistema.

En la mayoría de las fotografías y todos los telescopios, donde el sujeto está esencialmente infinitamente lejos, una distancia focal más larga (menor potencia óptica) conduce a una mayor ampliación y un ángulo de visión más estrecho; por el contrario, una distancia focal más corta o una potencia óptica más alta se asocian con un aumento más bajo y un ángulo de visión más amplio. Por otro lado, en aplicaciones como la microscopía en las que la ampliación se logra acercando el objeto a la lente, una distancia focal más corta (mayor potencia óptica) conduce a una mayor ampliación porque el sujeto puede acercarse al centro de proyección.

Aproximación de lente delgada

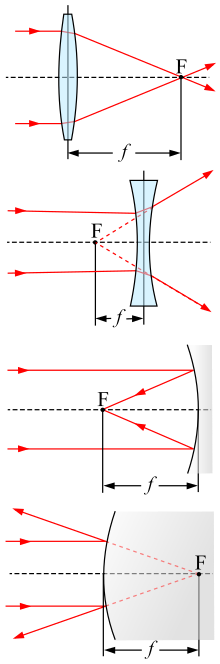
Para una lente delgada en el aire, la distancia focal es la distancia desde el centro de la lente hasta los focos principales (o puntos focales) de la lente. Para una lente convergente (por ejemplo, una lente convexa), la distancia focal es positiva y es la distancia a la que un haz de luz colimada se enfocará en un solo punto. Para una lente divergente (por ejemplo, una lente cóncava), la distancia focal es negativa y es la distancia al punto desde el cual un haz colimado parece divergir después de atravesar la lente.

Cuando se usa una lente para formar una imagen de algún objeto, la distancia del objeto a la lente u, la distancia de la lente a la imagen v, y la distancia focal f están relacionados por

1f=1u+1v.{displaystyle {frac} {f}={frac} {1}{u}+{frac} {1}{v}.}

La distancia focal de una lente delgada convexa se puede medir fácilmente usándola para formar una imagen de una fuente de luz distante en una pantalla. La lente se mueve hasta que se forma una imagen nítida en la pantalla. En este caso 1/u es despreciable, y la distancia focal viene dada por

f.. v.{displaystyle fapprox v}

Determinar la distancia focal de una lente cóncava es algo más difícil. La distancia focal de una lente de este tipo se considera el punto en el que los haces de luz que se propagan se encontrarían delante de la lente si la lente no estuviera allí. No se forma ninguna imagen durante dicha prueba, y la distancia focal debe determinarse pasando luz (por ejemplo, la luz de un rayo láser) a través de la lente, examinando cuánto se dispersa/dobla esa luz y siguiendo el rayo de luz. hacia atrás hasta el punto focal de la lente.

Sistemas ópticos generales

Diagrama de lentes gruesos

Para una lente gruesa (una que tiene un grosor no despreciable), o un sistema de imágenes que consta de varias lentes o espejos (por ejemplo, una lente fotográfica o un telescopio), la distancia focal suele ser llamado distancia focal efectiva (EFL), para distinguirlo de otros parámetros de uso común:

• Longitud focal frontal (FFL) or distancia focal (FFD) (FFD)s_F) es la distancia desde el punto focal frontal del sistema (F) hasta el vértice del primera superficie óptica (S₁).
• Longitud focal posterior (BFL) or distancia focal (BFD) (s_F′) es la distancia del vértice del última superficie óptica del sistema (S₂) al punto focal posterior (F′).

Para un sistema óptico en el aire, la distancia focal efectiva (f y f′) da la distancia desde los planos principales delantero y trasero (H y H′) a los focos correspondientes (F y F′). Si el medio circundante no es aire, la distancia se multiplica por el índice de refracción del medio (n es el índice de refracción de la sustancia de la que está hecha la lente; n₁ es el índice de refracción de cualquier medio delante de la lente; n₂ es el de cualquier medio detrás de ella). Algunos autores denominan a estas distancias las distancias focales delantera/trasera, distinguiéndolas de las distancias focales delantera/trasera, definidas anteriormente.

En general, la distancia focal o EFL es el valor que describe la capacidad del sistema óptico para enfocar la luz y es el valor que se utiliza para calcular la ampliación del sistema. Los otros parámetros se utilizan para determinar dónde se formará una imagen para una posición de objeto determinada.

Para el caso de una lente de espesor d en aire (n₁ = n₂ = 1), y superficies con radios de curvatura R₁ y R₂, la distancia focal efectiva f viene dada por la ecuación de Lensmaker:

1f=()n− − 1)()1R1− − 1R2+()n− − 1)dnR1R2),{displaystyle {frac {1} {f}=(n-1)left({frac} {1} {fn} {fnMicroc} {1}{2}}}} {fn1} {fn1}}}}derecho),}

donde n es el índice de refracción del medio de la lente. La cantidad 1/f también se conoce como la potencia óptica de la lente.

La distancia focal frontal correspondiente es:

FFD=f()1+()n− − 1)dnR2),{displaystyle {mbox{FFD}=fleft(1+{frac {(n-1)d}{nR_{2}}}right),}}

y la distancia focal posterior:

BFD=f()1− − ()n− − 1)dnR1).{displaystyle {mbox{BFD}=fleft(1-{frac {(n-1)d}{nR_{1}}}right).}

En la convención de signos utilizada aquí, el valor de R₁ será positivo si la primera superficie de la lente es convexa y negativa si es cóncava. El valor de R₂ es negativo si la segunda superficie es convexa y positivo si es cóncava. Tenga en cuenta que las convenciones de signos varían entre diferentes autores, lo que da como resultado diferentes formas de estas ecuaciones según la convención utilizada.

Para un espejo en el aire curvado esféricamente, la magnitud de la distancia focal es igual al radio de curvatura del espejo dividido por dos. La distancia focal es positiva para un espejo cóncavo y negativa para un espejo convexo. En la convención de signos utilizada en el diseño óptico, un espejo cóncavo tiene un radio de curvatura negativo, por lo que

f=− − R2,{displaystyle f=-{R over 2}

donde R es el radio de curvatura de la superficie del espejo.

Consulte Radio de curvatura (óptica) para obtener más información sobre la convención de signos para el radio de curvatura que se utiliza aquí.

En fotografía

Lente de 28 mm

Lente de 50 mm

Lente de 70 mm

Lente de 210 mm

Un ejemplo de cómo la elección de la lente afecta el ángulo de la vista. Las fotos arriba fueron tomadas por una cámara de 35 mm a una distancia fija del sujeto.

Imágenes de letras negras en una fina lente convexa de longitud focal f se muestran en rojo. Se muestran los rayos seleccionados para letras E, I y K en azul, verde y naranja, respectivamente. Note que E (a las 2f) tiene una imagen igual, real e invertida; I (a f) tiene su imagen en el infinito; y K (a f/2) tiene una imagen doble, virtual y vertical.

En esta simulación de ordenador, ajustar el campo de visión (cambiando la longitud focal) manteniendo el sujeto en marco (cambiando en consecuencia la posición de la cámara) resulta en imágenes muy diferentes. En las longitudes focales que se acercan al infinito (0 grados de campo de vista), los rayos de luz son casi paralelos entre sí, lo que resulta en el sujeto que se ve "planificado". En pequeñas longitudes focales (campo negro de vista), el sujeto aparece "exhortado".

Las distancias focales de las lentes de las cámaras se especifican generalmente en milímetros (mm), pero algunas lentes más antiguas están marcadas en centímetros (cm) o pulgadas.

La distancia focal (f) y el campo de visión (FOV) de una lente son inversamente proporcionales. Para una lente rectilínea estándar, FOV = 2 arctan x/2f, donde x es la diagonal de la película.

Cuando una lente fotográfica se ajusta a "infinito", su plano principal posterior se separa del sensor o la película, que luego se sitúa en el plano focal, por la distancia focal de la lente. Los objetos lejos de la cámara producen imágenes nítidas en el sensor o la película, que también se encuentra en el plano de la imagen.

Para mostrar objetos más cercanos con un enfoque nítido, la lente debe ajustarse para aumentar la distancia entre el plano principal posterior y la película, para colocar la película en el plano de la imagen. La distancia focal (f), la distancia desde el plano principal frontal al objeto a fotografiar (s₁), y la distancia desde el plano principal posterior al plano de la imagen (s₂) están entonces relacionados por:

1s1+1s2=1f.{fnMicroc} {1}{1}}+{frac} {1}{2}={frac} {1}{f}.}

A medida que se disminuye s₁, se debe aumentar s₂. Por ejemplo, considere una lente normal para una cámara de 35 mm con una distancia focal de f = 50 mm. Para enfocar un objeto distante (s₁ ≈ ∞), el plano principal posterior de la lente debe estar ubicado a una distancia s₂ = 50 mm desde el plano de la película, de modo que esté en la ubicación del plano de la imagen. Para enfocar un objeto a 1 m de distancia (s₁ = 1000 mm), la lente debe alejarse 2,6 mm del plano de la película, a s₂ = 52,6 mm.

La distancia focal de una lente determina el aumento con el que toma imágenes de objetos distantes. Es igual a la distancia entre el plano de la imagen y un agujero de alfiler que refleja objetos distantes del mismo tamaño que la lente en cuestión. Para lentes rectilíneos (es decir, sin distorsión de imagen), la imagen de objetos distantes está bien modelada como un modelo de cámara estenopeica. Este modelo conduce al modelo geométrico simple que usan los fotógrafos para calcular el ángulo de visión de una cámara; en este caso, el ángulo de visión depende únicamente de la relación entre la distancia focal y el tamaño de la película. En general, el ángulo de visión también depende de la distorsión.

Una lente con una distancia focal aproximadamente igual al tamaño de la diagonal de la película o el formato del sensor se conoce como lente normal; su ángulo de visión es similar al ángulo subtendido por una impresión lo suficientemente grande vista a una distancia de visualización típica de la diagonal de la impresión, que por lo tanto produce una perspectiva normal al ver la impresión; este ángulo de visión es de unos 53 grados en diagonal. Para las cámaras de formato completo de 35 mm, la diagonal es de 43 mm y una típica "normal" lente tiene una distancia focal de 50 mm. Un objetivo con una distancia focal más corta de lo normal suele denominarse objetivo gran angular (normalmente de 35 mm o menos, para cámaras de formato de 35 mm), mientras que un objetivo significativamente más largo de lo normal puede denominarse teleobjetivo (típicamente 85 mm y más, para cámaras de formato de 35 mm). Técnicamente, las lentes de distancia focal larga son solo "telefoto" si la distancia focal es más larga que la distancia física de la lente, pero el término se usa a menudo para describir cualquier lente de distancia focal larga.

Debido a la popularidad del estándar de 35 mm, las combinaciones de cámara y lente a menudo se describen en términos de su distancia focal equivalente a 35 mm, es decir, la distancia focal de una lente que tendría el mismo ángulo de visión, o campo de visión, si se utiliza en una cámara de fotograma completo de 35 mm. El uso de una distancia focal equivalente a 35 mm es particularmente común con las cámaras digitales, que a menudo usan sensores más pequeños que una película de 35 mm y, por lo tanto, requieren distancias focales correspondientemente más cortas para lograr un ángulo de visión determinado, por un factor conocido como factor de recorte.