Lógica temporal

En lógica, lógica temporal es cualquier sistema de reglas y simbolismo para representar y razonar sobre proposiciones cualificadas en términos de tiempo (por ejemplo, "yo soy siempre hambre", "Tendré eventualmente hambre", o "Tendré hambre hasta que coma algo";). A veces también se usa para referirse a la lógica temporal, un sistema de lógica temporal basado en la lógica modal introducido por Arthur Prior a fines de la década de 1950, con importantes contribuciones de Hans Kamp. Ha sido desarrollado aún más por informáticos, en particular Amir Pnueli, y lógicos.

La lógica temporal ha encontrado una aplicación importante en la verificación formal, donde se utiliza para establecer los requisitos de los sistemas de hardware o software. Por ejemplo, se puede desear decir que siempre se realiza una solicitud, eventualmente se otorga acceso a un recurso, pero nunca se otorga a dos solicitantes simultáneamente. Tal enunciado puede expresarse convenientemente en una lógica temporal.

Motivación

Considere la afirmación "Tengo hambre". Aunque su significado es constante en el tiempo, el valor de verdad de la declaración puede variar en el tiempo. A veces es verdadero, y a veces falso, pero nunca simultáneamente verdadero y falso. En una lógica temporal, un enunciado puede tener un valor de verdad que varía en el tiempo, en contraste con una lógica atemporal, que se aplica solo a enunciados cuyos valores de verdad son constantes en el tiempo. Este tratamiento del valor de verdad a lo largo del tiempo diferencia la lógica temporal de la lógica verbal computacional.

La lógica temporal siempre tiene la capacidad de razonar sobre una línea de tiempo. El llamado "tiempo lineal" las lógicas se restringen a este tipo de razonamiento. Sin embargo, las lógicas de tiempo ramificado pueden razonar sobre múltiples líneas de tiempo. Esto permite, en particular, el tratamiento de entornos que pueden actuar de forma impredecible. Para continuar con el ejemplo, en una lógica de tiempo de bifurcación podemos afirmar que "existe la posibilidad de que me quede con hambre para siempre" y que "existe la posibilidad de que finalmente ya no tenga hambre". #34;. Si no sabemos si alguna vez me alimentarán o no, estas afirmaciones pueden ser ambas ciertas.

Historia

Aunque la lógica de Aristóteles se ocupa casi por completo de la teoría del silogismo categórico, hay pasajes en su obra que ahora se ven como anticipaciones de la lógica temporal, y pueden implicar una forma temprana y parcialmente desarrollada de primera- orden bivalente modal lógico temporal. Aristóteles estaba particularmente preocupado por el problema de los contingentes futuros, donde no podía aceptar que el principio de bivalencia se aplica a declaraciones sobre eventos futuros, es decir, que podemos decidir en el presente si una declaración sobre un evento futuro es verdadera o falsa, como &# 34;habrá una batalla naval mañana".

Hubo poco desarrollo durante milenios, señaló Charles Sanders Peirce en el siglo XIX:

El tiempo generalmente ha sido considerado por los lógicas para ser lo que se llama materia 'extralógica'. Nunca he compartido esta opinión. Pero he pensado que la lógica aún no había alcanzado el estado de desarrollo en el que la introducción de modificaciones temporales de sus formas no daría lugar a una gran confusión; y soy mucho de esa manera de pensar todavía.

Sorprendentemente para Peirce, el primer sistema de lógica temporal se construyó, hasta donde sabemos, en la primera mitad del siglo XX. Aunque Arthur Prior es ampliamente conocido como uno de los fundadores de la lógica temporal, la primera formalización de dicha lógica fue proporcionada en 1947 por el lógico polaco Jerzy Łoś. En su trabajo Podstawy Analizy Metodologicznej Kanonów Milla (Los fundamentos de un análisis metodológico de los métodos de Mill) presentó una formalización de los cánones de Mill. En Łoś' enfoque, se hizo hincapié en el factor tiempo. Por lo tanto, para alcanzar su objetivo, tuvo que crear una lógica que pudiera proporcionar medios para la formalización de las funciones temporales. La lógica podría verse como un subproducto de Łoś' objetivo principal, aunque fue la primera lógica posicional que, como marco, se usó más tarde para Łoś' Invenciones en lógica epistémica. La lógica en sí tiene una sintaxis muy diferente a la lógica temporal de Prior, que utiliza operadores modales. El idioma de Łoś' la lógica utiliza más bien un operador de realización, específico de la lógica posicional, que vincula la expresión con el contexto específico en el que se considera su valor de verdad. En Łoś' trabajo este contexto considerado era sólo temporal, por lo que las expresiones se vinculaban con momentos o intervalos de tiempo específicos.

En los años siguientes, comenzó la investigación de la lógica temporal por parte de Arthur Prior. Estaba preocupado por las implicaciones filosóficas del libre albedrío y la predestinación. Según su esposa, consideró por primera vez formalizar la lógica temporal en 1953. Los resultados de su investigación se presentaron por primera vez en la conferencia en Wellington en 1954. El sistema que presentó Prior era similar sintácticamente a Łoś' lógica, aunque no fue hasta 1955 que se refirió explícitamente a Łoś' trabajo, en la última sección del Apéndice 1 en la Formal Logic de Prior.

Prior dio conferencias sobre el tema en la Universidad de Oxford entre 1955 y 1956, y en 1957 publicó un libro, Tiempo y modalidad, en el que introdujo una lógica modal proposicional con dos conectores temporales (operadores modales), F y P, correspondientes a "algún momento en el futuro" y "en algún momento del pasado". En este trabajo temprano, Prior consideraba que el tiempo era lineal. En 1958, sin embargo, recibió una carta de Saul Kripke, quien señaló que esta suposición quizás no esté justificada. En un desarrollo que presagiaba otro similar en la informática, Prior tomó esto como consejo y desarrolló dos teorías del tiempo de bifurcación, a las que llamó 'Ockhamist'. y "Peirceano". Entre 1958 y 1965, Prior también mantuvo correspondencia con Charles Leonard Hamblin, y una serie de desarrollos tempranos en el campo se pueden rastrear a esta correspondencia, por ejemplo, las implicaciones de Hamblin. Prior publicó su obra más madura sobre el tema, el libro Pasado, presente y futuro en 1967. Murió dos años después.

Junto con la lógica temporal, Prior construyó algunos sistemas de lógica posicional, que heredaron sus ideas principales de Łoś. El trabajo en lógicas temporales posicionales fue continuado por Nicholas Rescher en los años 60 y 70. En obras como Nota sobre lógica cronológica (1966), Sobre la lógica de las proposiciones cronológicas (1968), Lógica topológica (1968), y Lógica temporal (1971) investigó las conexiones entre Łoś' y los sistemas de Prior. Además, demostró que los operadores de tiempo de Prior podían definirse utilizando un operador de realización en lógicas posicionales específicas. Rescher, en su trabajo, también creó sistemas más generales de lógica posicional. Aunque los primeros se construyeron para usos puramente temporales, propuso el término lógica topológica para las lógicas que debían contener un operador de realización pero que no tenían axiomas temporales específicos, como el axioma del reloj.

Los operadores temporales binarios Desde y Hasta fueron presentados por Hans Kamp en su doctorado de 1968. tesis, que también contiene un resultado importante que relaciona la lógica temporal con la lógica de primer orden, un resultado que ahora se conoce como teorema de Kamps.

Dos de los primeros contendientes en las verificaciones formales fueron la lógica temporal lineal, una lógica de tiempo lineal de Amir Pnueli, y la lógica de árbol de cálculo (CLT), una lógica de tiempo ramificado de Mordechai Ben-Ari, Zohar Manna y Amir Pnueli. Casi al mismo tiempo, E. M. Clarke y E. A. Emerson sugirieron un formalismo casi equivalente a CTL. El hecho de que la segunda lógica pueda decidirse más eficientemente que la primera no se refleja en las lógicas de ramificación y de tiempo lineal en general, como se ha argumentado a veces. Más bien, Emerson y Lei muestran que cualquier lógica de tiempo lineal se puede extender a una lógica de tiempo ramificado que se puede decidir con la misma complejidad.

Łoś' lógica posicional

La lógica de Łoś se publicó como su tesis de maestría de 1947 Podstawy Analizy Metodologicznej Kanonów Milla (Los fundamentos de un análisis metodológico de los métodos de Mill). Sus conceptos filosóficos y formales podrían verse como una continuación de los de la Escuela de Lógica de Lviv-Varsovia, ya que su supervisor fue Jerzy Słupecki, discípulo de Jan Łukasiewicz. El artículo no se tradujo al inglés hasta 1977, aunque Henryk Hiż presentó en 1951 una reseña breve, pero informativa, en el Journal of Symbolic Logic. Esta revisión contenía conceptos centrales del trabajo de Łoś y fue suficiente para popularizar sus resultados entre la comunidad lógica. El objetivo principal de este trabajo fue presentar los cánones de Mill en el marco de la lógica formal. Para lograr este objetivo, el autor investigó la importancia de las funciones temporales en la estructura del concepto de Mill. Teniendo eso, proporcionó su sistema axiomático de lógica que encajaría como marco para los cánones de Mill junto con sus aspectos temporales.

Sintaxis

The language of the logic first published in Podstawy Analizy Metodologiczne Kanonów Millani> (The Foundations of a Methodological Analysis of Mill’s Methods) consisted of:

• operadores lógicos de primera orden ‘¬’, ‘∧’, ‘∨’, ‘→’, ‘ cuándo’, ‘ cuándo’ ’
• Operador de realización U
• símbolo funcional δ
• variables proposición p₁,p₂,p₃,...
• variables denotando momentos de tiempo t₁,t₂,t₃,...
• variables denotando intervalos de tiempo n₁,n₂,n₃,...

El conjunto de términos (indicado por S) se construye de la siguiente manera:

• variables denotando momentos de tiempo o intervalos son términos
• si τ τ ▪ ▪ S{displaystyle tau in S} y ε ε {displaystyle epsilon } es una variable intervalo de tiempo, entonces δ δ ()τ τ ,ε ε )▪ ▪ S{displaystyle delta (tauepsilon)in S}

El conjunto de fórmulas (denotado por For) se construye de la siguiente manera:

• todas las fórmulas lógicas de primer orden son válidas
• si τ τ ▪ ▪ S{displaystyle tau in S} y φ φ {displaystyle phi } es una variable proposicional, entonces Uτ τ ()φ φ )▪ ▪ For{displaystyle U_{tau }(phi)in For}
• si φ φ ▪ ▪ For{displaystyle phi in For}, entonces ¬ ¬ φ φ ▪ ▪ For{displaystyle neg phi in For}
• si φ φ ,↑ ↑ ▪ ▪ For{displaystyle phipsiin For} y ∘ ∘ ▪ ▪ {}∧ ∧ ,Alternativa Alternativa ,→ → ,↑ ↑ }{displaystyle circ in {wedgeveerightarrowequiv {}}, entonces φ φ ∘ ∘ ↑ ↑ ▪ ▪ For{displaystyle phi circ psi in For}
• si φ φ ▪ ▪ For{displaystyle phi in For} y Q▪ ▪ {}О О ,∃ ∃ }{displaystyle Qin {forallexists} y es una variable proposición, momento o intervalo, entonces Q.. φ φ ▪ ▪ For{displaystyle Q_{upsilon }phi in For}

Sistema Axiomático Original

1. Ut1¬ ¬ p1↑ ↑ ¬ ¬ Ut1p1{displaystyle U_{t_{1}neg p_{1}equiv neg U_{t_{1}p_{1}
2. Ut1()p1→ → p2)→ → ()Ut1p1→ → Ut1p2){displaystyle ¿Qué? (U_{t_{1}p_{1}derecho U_{t_{1}p_{2}}
3. Ut1()()p1→ → p2)→ → ()()p2→ → p3)→ → ()p1→ → p3))){displaystyle ¿Por qué?
4. Ut1()p1→ → ()¬ ¬ p1→ → p2)){displaystyle ¿Qué?
5. Ut1()()¬ ¬ p1→ → p1)→ → p1){displaystyle U_{t_{1}(neg p_{1}rightarrow ############## P_{1}}
6. О О t1Ut1p1→ → p1{displaystyle forall ¿Qué? P_{1}
7. О О t1О О n1∃ ∃ t2О О p1()Uδ δ ()t1,n1)p1↑ ↑ Ut2p1){displaystyle forall Para todos ### {n_{1}exists Para todos ¿Qué? (t_{1},n_{1}p_{1}equiv U_{t_{2}p_{1}}
8. О О t1О О n1∃ ∃ t2О О p1()Uδ δ ()t2,n1)p1↑ ↑ Ut1p1){displaystyle forall Para todos ### {n_{1}exists Para todos ¿Qué? (t_{2},n_{1}p_{1}equiv U_{t_{1}p_{1}}
9. О О t1∃ ∃ p1О О t2()Ut2p1↑ ↑ О О p2()Ut1p2↑ ↑ Ut2p2)){displaystyle forall _{t_{1}exists Para todos ¿Qué? ################################################################################################################################################################################################################################################################ U_{t_{2}p_{2})}

Did you mean:

Prior 's tense logic (TL)

La lógica del tiempo verbal introducida en Tiempo y modalidad tiene cuatro operadores modales (no funcionales de verdad) (además de todos los operadores funcionales de verdad habituales en la lógica proposicional de primer orden).

• P"Fue el caso que..." (P significa "past")
• F"Es el caso que..." (F significa "futuro")
• G"Siempre será el caso que..."
• H"Siempre fue el caso que..."

Estos se pueden combinar si dejamos que π sea un camino infinito:

• π π ⊨ ⊨ FGφ φ {displaystyle pi vDash FGphi }: "En cierto punto, φ φ {displaystyle phi } es verdad en todos los estados futuros del camino"
• π π ⊨ ⊨ GFφ φ {displaystyle pi vDash GFphi }:φ φ {displaystyle phi } es verdad en infinitamente muchos estados en el camino"

De P y F se puede definir G y H, y viceversa:

F↑ ↑ ¬ ¬ G¬ ¬ P↑ ↑ ¬ ¬ H¬ ¬ {displaystyle {begin{aligned} F Pulsequiv lnot Glnot \pctavequiv lnot Hlnot end{aligned}}

Sintaxis y semántica

Se especifica una sintaxis mínima para TL con la siguiente gramática BNF:

φ φ ::=aSilencio⊥ ⊥ Silencio¬ ¬ φ φ Silencioφ φ Alternativa Alternativa φ φ SilencioGφ φ SilencioHφ φ {displaystyle phi::=a; WordPress;bot; Tortura;lnot phi; sufrimiento;phi lor phi phi ;

donde a es alguna fórmula atómica.

Los modelos de Kripke se utilizan para evaluar la verdad de las oraciones en TL. Un par (T, <) de un conjunto T y una relación binaria < en T (llamado "precedencia") se llama un marco. Un modelo viene dado por triple (T, <, V ) de un marco y una función V llamada valoración que asigna a cada par (a, u) de una fórmula atómica y un valor de tiempo algún valor de verdad. La noción "ϕ es verdadera en un modelo U=(T, <, V) en el momento u" se abrevia U⊨ϕ[u]. Con esta notación,

Estado	... es verdad justo cuando
U⊨a[u]	V()a,u)=true
U⊨φ[u]	no U⊨φ[u]
U⊨φ∧↑[u]	U⊨φ[u] y U⊨↑[u]
U⊨φAlternativa↑[u]	U⊨φ[uO U⊨↑[u]
U⊨φ→↑[u]	U⊨↑[uSi U⊨φ[u]
U⊨Gφ[u]	U⊨φ[vPara todos v con u.v
U⊨ Hφ[u]	U⊨φ[vPara todos v con v.u

Dada una clase F de marcos, una oración ϕ de TL es

• válido con respecto a F si por cada modelo U=T,VCon...Ten F y para todos u dentro T, U⊨φ[u]
• satisfizo con respecto a F si hay un modelo U=T,VCon...Ten F tal que para algunos u dentro T, U⊨φ[u]
• a consecuencia de una sentencia ↑ con respecto a F si por cada modelo U=T,VCon...Ten F y para todos u dentro T, si U⊨↑[uEntonces U⊨φ[u]

Muchas oraciones solo son válidas para una clase limitada de marcos. Es común restringir la clase de marcos a aquellos con una relación < que es transitivo, antisimétrico, reflexivo, tricotómico, irreflexivo, total, denso o alguna combinación de estos.

Una lógica axiomática mínima

Burgess describe una lógica que no hace suposiciones sobre la relación <, pero permite deducciones significativas, basadas en el siguiente esquema axiomático:

1. A Donde A es una tautología de la lógica de primer orden
2. G(A→B)→(GA→GB)
3. H(A→B)→(HA→ HB)
4. A→GPA
5. A→HFA

con las siguientes reglas de deducción:

1. dado A→B y A, deduce B (modus ponens)
2. dado una tautología A, infer GA
3. dado una tautología A, infer HA

Se pueden derivar las siguientes reglas:

1. La regla de Becker: dado A→B, deduce TA→TB donde T es un tenso, cualquier secuencia hecha de G, H, F y P.
2. Espejo: dado un teorema A, deducir su declaración del espejo A^§, que se obtiene reemplazando G por H (y así F por P) y viceversa.
3. Dualidad: dado un teorema A, deducir su doble declaración A*, que se obtiene por intercambiar ∧ con ∨, G con F, y H con P.

Traducción a lógica de predicados

Burgess ofrece una traducción de Meredith de declaraciones en TL a declaraciones en lógica de primer orden con una variable libre x₀ (que representa el momento presente). Esta traducción M se define recursivamente de la siguiente manera:

<math alttext="{displaystyle {begin{aligned}&M(a)&&=a^{*}x_{0}\&M(lnot phi)&&=lnot M(phi)\&M(phi land psi)&&=M(phi)land M(psi)\&M({mathsf {G}}phi)&&=forall x_{1}(x_{0}<x_{1}rightarrow M(A^{+}))\&M({mathsf {H}}phi)&&=forall x_{1}(x_{1}M()a)=aAlternativa Alternativa x0M()¬ ¬ φ φ )=¬ ¬ M()φ φ )M()φ φ ∧ ∧ ↑ ↑ )=M()φ φ )∧ ∧ M()↑ ↑ )M()Gφ φ )=О О x1()x0.x1→ → M()A+))M()Hφ φ )=О О x1()x1.x0→ → M()A+)){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cH} {f}} {f}f}f}f} {f}f}f} {f}f}f}f} {f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMincip]cnMinMinMinMinMinMinMinMinMin<img alt="{displaystyle {begin{aligned}&M(a)&&=a^{*}x_{0}\&M(lnot phi)&&=lnot M(phi)\&M(phi land psi)&&=M(phi)land M(psi)\&M({mathsf {G}}phi)&&=forall x_{1}(x_{0}<x_{1}rightarrow M(A^{+}))\&M({mathsf {H}}phi)&&=forall x_{1}(x_{1}

Donde A+{displaystyle A^{+} es la sentencia A{displaystyle A} con todos los índices variables aumentados por 1 y aAlternativa Alternativa {displaystyle a^{*} es un predicado de un lugar definido por x↦ ↦ V()a,x){displaystyle xmapsto V(a,x)}.

Operadoras temporales

(feminine)

La lógica temporal tiene dos tipos de operadores: operadores lógicos y operadores modales. Los operadores lógicos son operadores habituales de funcionamiento de la verdad (¬ ¬ ,Alternativa Alternativa ,∧ ∧ ,→ → {displaystyle neglorlandrightarrow }). Los operadores modales utilizados en lógica temporal lineal y lógica de árbol de computación se definen como sigue.

Textual	Símbolo	Definición	Explicación	Diagrama
Operadores binarios
φ U ↑	φ φ U↑ ↑ {displaystyle phi ~{mathcal {U}~psi }	<math alttext="{displaystyle (B,{mathcal {U}},C)(phi)= (exists i:C(phi _{i})land (forall j()BUC)()φ φ )=()∃ ∃ i:C()φ φ i)∧ ∧ ()О О j.i:B()φ φ j))){displaystyle (B,{mathcal {U},C)(phi)=exists i:C(phi _{i})land (forall j madei:B(phi _{j})})}<img alt="{displaystyle (B,{mathcal {U}},C)(phi)= (exists i:C(phi _{i})land (forall j	Until: ↑ mantiene en la posición actual o futura, y φ tiene que mantenerse hasta esa posición. En esa posición φ no tiene que aguantar más.
φ R ↑	φ φ R↑ ↑ {displaystyle phi ~{mathcal {R}~psi }	<math alttext="{displaystyle (B,{mathcal {R}},C)(phi)= (forall i:C(phi _{i})lor (exists j()BRC)()φ φ )=()О О i:C()φ φ i)Alternativa Alternativa ()∃ ∃ j.i:B()φ φ j))){displaystyle (B,{mathcal {R},C)(phi)=(forall i:C(phi _{i})lor (exists j madei:B(phi _{j})})}<img alt="{displaystyle (B,{mathcal {R}},C)(phi)= (forall i:C(phi _{i})lor (exists j	RElease: φ liberaciones ↑ si ↑ es cierto hasta e incluyendo la primera posición en la que φ es verdad (o para siempre si tal posición no existe).
Operadores no autorizados
N φ	◯ ◯ φ φ {displaystyle bigcirc phi }	NB()φ φ i)=B()φ φ i+1){displaystyle {mathcal {N}B(phi _{i})=B(phi _{i+1}}	Next: φ tiene que mantenerse en el próximo estado. ()X se utiliza sinónimo.)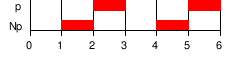
F φ	Cause Cause φ φ {displaystyle Diamond phi }	FB()φ φ )=()trueUB)()φ φ ){fnMicrosoft Sans Serif}fnMicrosoft Sans Serif}	Future: φ eventualmente tiene que sostener (alguna parte en el camino posterior).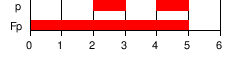
G φ	▪ ▪ φ φ {displaystyle Box phi }	GB()φ φ )=¬ ¬ F¬ ¬ B()φ φ ){displaystyle {mathcal {}B(phi)=neg {mathcal {F}neg B(phi)}	GLobally: φ tiene que aferrarse a todo el camino subsiguiente.
A φ	О О φ φ {displaystyle forall phi }	()AB)()↑ ↑ )=()О О φ φ :φ φ 0=↑ ↑ → → B()φ φ )){displaystyle ({mathcal {}A}B)(psi)=(forall phi:phi _{0}=psi to B(phi)}	All: φ tiene que mantenerse en todos los caminos desde el estado actual.
E φ	∃ ∃ φ φ {displaystyle exists phi }	()EB)()↑ ↑ )=()∃ ∃ φ φ :φ φ 0=↑ ↑ ∧ ∧ B()φ φ )){displaystyle ({mathcal {}E}B)(psi)= (exists phi:phi _{0}=psi land B(phi)}	Exists: existe al menos un camino desde el estado actual donde φ sostiene.

Símbolos alternativos:

• operador R a veces se denota V
• El operador W es débil hasta operador: fWg{displaystyle fmathbf {W} g} equivale a fUgAlternativa Alternativa Gf{displaystyle fmathbf {U} glor mathbf {G} f}

Los operadores unarios son fórmulas bien formadas cuando B(φ) está bien formado. Los operadores binarios son fórmulas bien formadas siempre que B(φ) y C(φ) están bien formados.

En algunas lógicas, algunos operadores no se pueden expresar. Por ejemplo, el operador N no se puede expresar en lógica temporal de acciones.

Lógicas temporales

Las lógicas temporales incluyen:

• Algunos sistemas de lógica posicional
• Lógica temporal lineal (LTL) lógica temporal sin plazos ramificados
• Lógica del árbol de computación (CTL) lógica temporal con líneas de tiempo ramificado
• Lógica intervaloraria temporal (ITL)
• Lógica temporal de acciones (TLA)
• Lógica temporal de signos (STL)
• Lógica temporal (TTL)
• Idioma de especificación de bienes (PSL)
• CTL*, que generaliza LTL y CTL
• Hennessy–Milner logic (HML)
• Modal μ-calculus, que incluye como subconjunto HML y CTL*
• Lógica temporal métrica (MTL)
• Lógica temporal de intervalo métrico (MITL)
• Lógica temporal proposiciónl (TPTL)
• Lógica temporal truncada (TLTL)
• Lógica hipertemporal (HyperLTL)

Did you mean:

A variation, closely related to temporal or chronological or tense logics, are modal logics based upon n#34;topology", "place", or "spatial position#34;.