Lóbulo de Roche

Este es un esquema de un sistema binario semidepartido con el componente más grande llenando su lóbulo Roche (línea negra).

En astronomía, el lóbulo de Roche es la región alrededor de una estrella en un sistema binario dentro del cual el material en órbita está unido gravitacionalmente a esa estrella. Es una región aproximadamente en forma de lágrima delimitada por un equipotencial gravitacional crítico, con el vértice de la lágrima apuntando hacia la otra estrella (el vértice está en el punto L1 Lagrangiano del sistema).

El lóbulo de Roche es diferente de la esfera de Roche, que se aproxima a la esfera de influencia gravitatoria de un cuerpo astronómico frente a las perturbaciones de un cuerpo más masivo alrededor del cual orbita. También es diferente del límite de Roche, que es la distancia a la que un objeto que se mantiene unido solo por la gravedad comienza a romperse debido a las fuerzas de marea. El lóbulo de Roche, el límite de Roche y la esfera de Roche llevan el nombre del astrónomo francés Édouard Roche.

Definición

Una representación tridimensional del potencial de Roche en una estrella binaria con una relación de masa de 2, en el marco co-rotante. Las figuras en forma de goteo en la parcela de equipotential en la parte inferior de la figura definen lo que se consideran los lóbulos de Roche de las estrellas. L1, L2 y L3 son los puntos Lagrangian donde las fuerzas (consideradas en el marco giratorio) cancelan. La misa puede fluir a través del punto de silla L1 de una estrella a su compañero, si la estrella llena su lóbulo de Roche.

Modelo 3D STL del potencial de Roche de dos cuerpos orbitales, representado medio como superficie y medio como malla

En un sistema binario con una órbita circular, suele ser útil describir el sistema en un sistema de coordenadas que gira junto con los objetos. En este marco no inercial, se debe considerar la fuerza centrífuga además de la gravedad. Los dos juntos pueden describirse mediante un potencial, de modo que, por ejemplo, las superficies estelares se encuentran a lo largo de superficies equipotenciales.

Cerca de cada estrella, las superficies de igual potencial gravitacional son aproximadamente esféricas y concéntricas con la estrella más cercana. Lejos del sistema estelar, las equipotenciales son aproximadamente elipsoidales y alargadas paralelas al eje que une los centros estelares. Una equipotencial crítica se corta a sí misma en el punto L1 Lagrangiano del sistema, formando una figura de ocho de dos lóbulos con una de las dos estrellas en el centro de cada lóbulo. Esta equipotencial crítica define los lóbulos de Roche.

Cuando la materia se mueve en relación con el marco co-rotatorio, parecerá que actúa sobre ella una fuerza de Coriolis. Esto no se puede derivar del modelo de lóbulo de Roche ya que la fuerza de Coriolis es una fuerza no conservativa (es decir, no representable por un potencial escalar).

Más análisis

array potencial

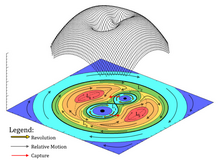
En los gráficos de potencial de gravedad, L₁, L₂, L₃, L₄, L ₅ están en rotación síncrona con el sistema. Las regiones de rojo, naranja, amarillo, verde, azul claro y azul son matrices potenciales de mayor a menor. Las flechas rojas son la rotación del sistema y las flechas negras son los movimientos relativos de los escombros.

Los desechos van más rápido en la región de menor potencial y más lentos en la región de mayor potencial. Por lo tanto, los movimientos relativos de los desechos en la órbita inferior tienen la misma dirección que la revolución del sistema, mientras que en la órbita superior son opuestos.

L₁ es el punto de equilibrio de captura gravitacional. Es un punto de corte de gravedad del sistema estelar binario. Es el equilibrio de potencial mínimo entre L₁, L₂, L₃, L₄ y L₅. Es la forma más fácil para que los escombros se desplacen entre una esfera de Hill (un círculo interior de azul y azul claro) y regiones de gravedad comunales (figuras de ocho de amarillo y verde en el lado interior).

Esfera de colina y órbita herradura

L₂ y L₃ son puntos de equilibrio de perturbaciones gravitacionales. Pasando a través de estos dos puntos de equilibrio, los escombros pueden conmutar entre la región externa (forma de ocho de amarillo y verde en el lado exterior) y la región de gravedad comunal del sistema binario.

L₄ y L₅ son los puntos de potencial máximo en el sistema. Son equilibrios inestables. Si la proporción de masa de las dos estrellas aumenta, las regiones naranja, amarilla y verde se convertirán en una órbita de herradura.

La región roja se convertirá en la órbita del renacuajo.

Transferencia de masa

Cuando una estrella "excede su lóbulo de Roche", su superficie se extiende más allá de su lóbulo de Roche y el material que se encuentra fuera del lóbulo de Roche puede "caerse" en el lóbulo de Roche del otro objeto a través del primer punto de Lagrange. En la evolución binaria esto se conoce como transferencia de masa a través del desbordamiento del lóbulo de Roche.

En principio, la transferencia de masa podría conducir a la desintegración total del objeto, ya que una reducción de la masa del objeto hace que su lóbulo de Roche se encoja. Sin embargo, hay varias razones por las que esto no sucede en general. En primer lugar, una reducción de la masa de la estrella donante puede hacer que la estrella donante también se encoja, lo que posiblemente impida tal resultado. En segundo lugar, con la transferencia de masa entre los dos componentes binarios, también se transfiere el momento angular. Mientras que la transferencia de masa de un donante más masivo a un acretor menos masivo generalmente conduce a una órbita que se encoge, lo contrario hace que la órbita se expanda (bajo el supuesto de conservación de la masa y el momento angular). La expansión de la órbita binaria conducirá a una contracción menos dramática o incluso a una expansión del lóbulo de Roche del donante, a menudo evitando la destrucción del donante.

Para determinar la estabilidad de la transferencia de masa y, por tanto, el destino exacto de la estrella donante, es necesario tener en cuenta cómo reaccionan el radio de la estrella donante y el de su lóbulo de Roche a la pérdida de masa de la donante; si la estrella se expande más rápido que su lóbulo de Roche o se encoge menos rápidamente que su lóbulo de Roche durante un tiempo prolongado, la transferencia de masa será inestable y la estrella donante puede desintegrarse. Si la estrella donante se expande con menos rapidez o se encoge más rápido que su lóbulo de Roche, la transferencia de masa generalmente será estable y puede continuar durante mucho tiempo.

La transferencia de masa debido al desbordamiento del lóbulo de Roche es responsable de una serie de fenómenos astronómicos, incluidos los sistemas Algol, las novas recurrentes (estrellas binarias que consisten en una gigante roja y una enana blanca que están lo suficientemente cerca como para que el material de la gigante roja gotee hacia abajo en la enana blanca), binarias de rayos X y púlsares de milisegundos. Tal transferencia de masa por desbordamiento del lóbulo de Roche (RLOF) se divide en tres casos distintos:

Caso A

El caso A RLOF ocurre cuando la estrella donante está quemando hidrógeno. Según Nelson y Eggleton, hay una serie de subclases que se reproducen aquí:

AD dinámica

cuando RLOF le sucede a una estrella con una zona de convección profunda. La transferencia de masa ocurre rápidamente en la escala de tiempo dinámica de la estrella y puede terminar con una fusión completa.

Contacto rápido AR

similar a AD, pero a medida que la estrella en la que la materia se acumula rápidamente gana masa, gana el tamaño físico suficiente para alcanzar su propio lóbulo de Roche. En tales ocasiones, el sistema se manifiesta como un contacto binario como una variable W Ursae Majoris.

AS contacto lento

similar a AR, pero solo ocurre un período corto de transferencia de masa rápida seguido de un período mucho más largo de transferencia de masa lenta. Eventualmente, las estrellas entrarán en contacto, pero habrán cambiado sustancialmente en el momento en que esto suceda. Las variables algol son el resultado de tales situaciones.

Adelantar antes de tiempo por AE

similar a AS, pero la estrella que gana masa supera a la estrella que dona masa para evolucionar más allá de la secuencia principal. La estrella donante puede encogerse tanto como para detener la transferencia de masa, pero eventualmente la transferencia de masa comenzará de nuevo a medida que la evolución estelar continúa y conduce a los casos.

Adelantos tardíos de la AL

el caso en que la estrella que inicialmente era la donante sufre una supernova después de que la otra estrella haya pasado por su propia ronda de RLOF.

AB binario

el caso en el que las estrellas cambian de un lado a otro entre las cuales una está experimentando RLOF al menos tres veces (técnicamente una subclase de las anteriores).

Una no adelantamiento

el caso en que la estrella que inicialmente era la donante experimenta una supernova antes de que la otra estrella alcance una fase RLOF.

Gigante AG

La transferencia de masa no comienza hasta que la estrella alcanza la rama gigante roja, pero antes de que haya agotado su núcleo de hidrógeno (después de lo cual el sistema se describe como Caso B).

Caso B

El caso B ocurre cuando RLOF comienza mientras el donante es una estrella que quema hidrógeno después del núcleo o una capa de hidrógeno. Este caso se puede subdividir en clases Br y Bc según si la transferencia de masa ocurre desde una estrella dominada por una zona de radiación (Br) y, por lo tanto, evoluciona como la situación con la mayoría del Caso A RLOF o una zona convectiva (Bc) después de la cual una puede ocurrir una fase de envolvente común (similar al Caso C). Una división alternativa de casos es Ba, Bb y Bc, que corresponden aproximadamente a las fases RLOF que ocurren durante la fusión de helio, después de la fusión de helio pero antes de la fusión de carbono, o después de la fusión de carbono en la estrella altamente evolucionada.

Caso C

El caso C ocurre cuando RLOF comienza cuando el donante está en la fase de combustión de la capa de helio o más allá. Estos sistemas son los más raros observados, pero esto puede deberse a un sesgo de selección.

Geometría

La forma precisa del lóbulo de Roche depende de la relación de masa q=M1/M2{displaystyle q=M_{1}/M_{2}, y debe ser evaluado numéricamente. Sin embargo, para muchos propósitos es útil aproximar el lóbulo de Roche como una esfera del mismo volumen. Una fórmula aproximada para el radio de esta esfera es

r1A=max[f1,f2]{fnMicroc} {} {fn}}=máximo {[f_{1},f_{2}}}, para <math alttext="{displaystyle 0<q0.q.20{displaystyle 0 won2}<img alt="{displaystyle 0<q

Donde f1=0,38+0.2log⁡ ⁡ q{displaystyle f_{1}=0.38+0.2log {q} y f2=0.46224()q1+q)1/3{displaystyle f_{2}=0.46224left({frac {q}{1+q}right)^{1/3}. Función f1{displaystyle f_{1} es mayor que f2{displaystyle f_{2} para q≳ ≳ 0,5228{displaystyle qgtrsim 0.5228}. La longitud A es la separación orbital del sistema y r₁ es el radio de la esfera cuyo volumen aproxima el lóbulo Roche de masa M₁. Esta fórmula es precisa en aproximadamente 2%. Otra fórmula aproximada fue propuesta por Eggleton y dice lo siguiente:

r1A=0.49q2/30.6q2/3+In⁡ ⁡ ()1+q1/3){fnMicroc} {} {fn} {fnK}} {fnMicroc}} {f}}} {fn}}} {f}}} {fn}} {fn}}}} {fnK}}}} {fn}}} {fnf}}}} {fnMicroc}}}}}}} {f}}}}} {f}}}}} {f}}}}}}} {f}}}} {f} {f}}}}}} {f}} {f} {f}} {f}f}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f}f}}f}}}}}f} {f}f}f}}}}}}}f}f}f}f}f}f}f}}}}}}} {0.49q^{2/3}{0.6q^{2/3}+ln(1+q^{1/3}}}}}.

Esta fórmula da resultados de hasta 1% de precisión sobre todo el rango de la relación de masa q{displaystyle q}.