Lista de momentos de inercia

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El Momento de inercia, denotado por $I$ , mide el grado en que un objeto resiste la aceleración de rotación alrededor de un eje particular, es el análogo rotacional de la masa (que determina la resistencia de un objeto a la aceleración lineal). Los momentos de inercia de una masa tienen unidades de dimensión ML² ([masa] × [longitud]²). No debe confundirse con el segundo momento de área, que tiene unidades de dimensión L⁴ ([longitud]⁴) y se utiliza en los cálculos de vigas. El momento de inercia de la masa a menudo también se conoce como inercia rotacional y, a veces, como masa angular.

Para objetos simples con simetría geométrica, a menudo se puede determinar el momento de inercia en una expresión exacta de forma cerrada. Normalmente, esto ocurre cuando la densidad de masa es constante, pero en algunos casos la densidad también puede variar en todo el objeto. En general, puede que no sea sencillo expresar simbólicamente el momento de inercia de formas con distribuciones de masa más complicadas y carentes de simetría. Al calcular los momentos de inercia, es útil recordar que es una función aditiva y aprovechar los teoremas de los ejes paralelos y perpendiculares.

Este artículo considera principalmente distribuciones de masa simétricas, con densidad constante en todo el objeto, y se considera que el eje de rotación pasa por el centro de masa, a menos que se especifique lo contrario.

Momentos de inercia

A continuación se muestran los momentos escalares de inercia. En general, el momento de inercia es un tensor, ver más abajo.

Description	Figure	Moment(s) of inertia
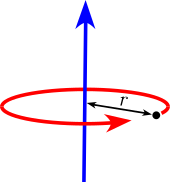
Point mass M at a distance r from the axis of rotation. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved.		${displaystyle I=Mr^{2}}$
Two point masses, m₁ and m₂, with reduced mass μ and separated by a distance x, about an axis passing through the center of mass of the system and perpendicular to the line joining the two particles.		${displaystyle I={frac {m_{1}m_{2}}{m_{1}!+!m_{2}}}x^{2}=mu x^{2}}$
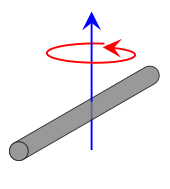
Thin rod of length L and mass m, perpendicular to the axis of rotation, rotating about its center. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0.		${displaystyle I_{mathrm {center} }={frac {1}{12}}mL^{2},!}$
Thin rod of length L and mass m, perpendicular to the axis of rotation, rotating about one end. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0.		${displaystyle I_{mathrm {end} }={frac {1}{3}}mL^{2},!}$
Thin circular loop of radius r and mass m. This is a special case of a torus for a = 0 (see below), as well as of a thick-walled cylindrical tube with open ends, with r₁ = r₂ and h = 0.		$I_{z}=mr^{2}!$ ${displaystyle I_{x}=I_{y}={frac {1}{2}}mr^{2},!}$
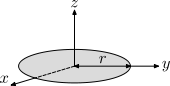
Thin, solid disk of radius r and mass m. This is a special case of the solid cylinder, with h = 0. That $I_{x}=I_{y}={frac {I_{z}}{2}},$ is a consequence of the perpendicular axis theorem.		${displaystyle I_{z}={frac {1}{2}}mr^{2},!}$ ${displaystyle I_{x}=I_{y}={frac {1}{4}}mr^{2},!}$
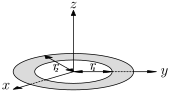
A uniform annulus (disk with a concentric hole) of mass m, inner radius r₁ and outer radius r₂		${displaystyle I_{z}={frac {1}{2}}m(r_{1}^{2}+r_{2}^{2})}$ ${displaystyle I_{x}=I_{y}={frac {1}{4}}m(r_{1}^{2}+r_{2}^{2})}$
An annulus with a constant area density $rho _{A}$		${displaystyle I_{z}={frac {1}{2}}pi rho _{A}(r_{2}^{4}-r_{1}^{4})}$ ${displaystyle I_{x}=I_{y}={frac {1}{4}}pi rho _{A}(r_{2}^{4}-r_{1}^{4})}$
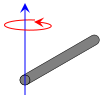
Thin cylindrical shell with open ends, of radius r and mass m. This expression assumes that the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r₁ = r₂. Also, a point mass m at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration.		${displaystyle Iapprox mr^{2},!}$
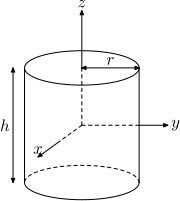
Solid cylinder of radius r, height h and mass m. This is a special case of the thick-walled cylindrical tube, with r₁ = 0.		${displaystyle I_{z}={frac {1}{2}}mr^{2},!}$ ${displaystyle I_{x}=I_{y}={frac {1}{12}}mleft(3r^{2}+h^{2}right)}$
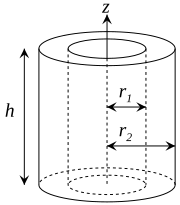
Thick-walled cylindrical tube with open ends, of inner radius r₁, outer radius r₂, length h and mass m.		${displaystyle I_{z}={frac {1}{2}}mleft(r_{2}^{2}+r_{1}^{2}right)=mr_{2}^{2}left(1-t+{frac {t^{2}}{2}}right)}$ where t = (r₂ − r₁)/r₂ is a normalized thickness ratio; ${displaystyle I_{x}=I_{y}={frac {1}{12}}mleft(3left(r_{2}^{2}+r_{1}^{2}right)+h^{2}right)}$ The above formula is for the xy plane passing through the center of mass, which coincides with the geometric center of the cylinder. If the xy plane is at the base of the cylinder, i.e. offset by ${displaystyle d={frac {h}{2}},}$ then by the parallel axis theorem the following formula applies: ${displaystyle I_{x}=I_{y}={frac {1}{12}}mleft(3left(r_{2}^{2}+r_{1}^{2}right)+4h^{2}right)}$
With a density of ρ and the same geometry		${displaystyle I_{z}={frac {pi rho h}{2}}left(r_{2}^{4}-r_{1}^{4}right)}$ ${displaystyle I_{x}=I_{y}={frac {pi rho h}{12}}left(3(r_{2}^{4}-r_{1}^{4})+h^{2}(r_{2}^{2}-r_{1}^{2})right)}$
Regular tetrahedron of side s and mass m with an axis of rotation passing through a tetrahedron's vertex and its center of mass		${displaystyle I_{mathrm {solid} }={frac {1}{20}}ms^{2},!}$ ${displaystyle I_{mathrm {hollow} }={frac {1}{12}}ms^{2},!}$
Regular octahedron of side s and mass m		${displaystyle I_{x,mathrm {hollow} }=I_{y,mathrm {hollow} }=I_{z,mathrm {hollow} }={frac {1}{6}}ms^{2},!}$ ${displaystyle I_{x,mathrm {solid} }=I_{y,mathrm {solid} }=I_{z,mathrm {solid} }={frac {1}{10}}ms^{2},!}$
Regular dodecahedron of side s and mass m		${displaystyle I_{x,mathrm {hollow} }=I_{y,mathrm {hollow} }=I_{z,mathrm {hollow} }={frac {39phi +28}{90}}ms^{2}}$ ${displaystyle I_{x,mathrm {solid} }=I_{y,mathrm {solid} }=I_{z,mathrm {solid} }={frac {39phi +28}{150}}ms^{2},!}$ (where $phi ={frac {1+{sqrt {5}}}{2}}$ )
Regular icosahedron of side s and mass m		${displaystyle I_{x,mathrm {hollow} }=I_{y,mathrm {hollow} }=I_{z,mathrm {hollow} }={frac {phi ^{2}}{6}}ms^{2}}$ ${displaystyle I_{x,mathrm {solid} }=I_{y,mathrm {solid} }=I_{z,mathrm {solid} }={frac {phi ^{2}}{10}}ms^{2},!}$
Hollow sphere of radius r and mass m.		${displaystyle I={frac {2}{3}}mr^{2},!}$
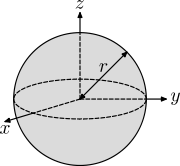
Solid sphere (ball) of radius r and mass m.		${displaystyle I={frac {2}{5}}mr^{2},!}$
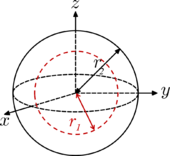
Sphere (shell) of radius r₂ and mass m, with centered spherical cavity of radius r₁. When the cavity radius r₁ = 0, the object is a solid ball (above). When r₁ = r₂, ${displaystyle {frac {r_{2}^{5}-r_{1}^{5}}{r_{2}^{3}-r_{1}^{3}}}={frac {5}{3}}r_{2}^{2}}$ , and the object is a hollow sphere.		${displaystyle I={frac {2}{5}}mcdot {frac {r_{2}^{5}-r_{1}^{5}}{r_{2}^{3}-r_{1}^{3}}},!}$
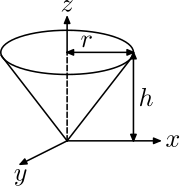
Right circular cone with radius r, height h and mass m		${displaystyle I_{z}={frac {3}{10}}mr^{2},!}$ About an axis passing through the tip: ${displaystyle I_{x}=I_{y}=mleft({frac {3}{20}}r^{2}+{frac {3}{5}}h^{2}right),!}$ About an axis passing through the base: ${displaystyle I_{x}=I_{y}=mleft({frac {3}{20}}r^{2}+{frac {1}{10}}h^{2}right),!}$ About an axis passing through the center of mass: ${displaystyle I_{x}=I_{y}=mleft({frac {3}{20}}r^{2}+{frac {3}{80}}h^{2}right),!}$
Right circular hollow cone with radius r, height h and mass m		${displaystyle I_{z}={frac {1}{2}}mr^{2},!}$ ${displaystyle I_{x}=I_{y}={frac {1}{4}}mleft(r^{2}+2h^{2}right),!}$
Torus with minor radius a, major radius b and mass m.		About an axis passing through the center and perpendicular to the diameter: ${displaystyle {frac {1}{4}}mleft(4b^{2}+3a^{2}right)}$ About a diameter: ${displaystyle {frac {1}{8}}mleft(5a^{2}+4b^{2}right)}$
Ellipsoid (solid) of semiaxes a, b, and c with mass m		${displaystyle I_{x}={frac {1}{5}}mleft(b^{2}+c^{2}right),!}$ ${displaystyle I_{y}={frac {1}{5}}mleft(a^{2}+c^{2}right),!}$ ${displaystyle I_{z}={frac {1}{5}}mleft(a^{2}+b^{2}right),!}$
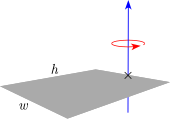
Thin rectangular plate of height h, width w and mass m (Axis of rotation at the end of the plate)		${displaystyle I_{e}={frac {1}{12}}mleft(4h^{2}+w^{2}right),!}$
Thin rectangular plate of height h, width w and mass m (Axis of rotation at the center)		${displaystyle I_{c}={frac {1}{12}}mleft(h^{2}+w^{2}right),!}$
Thin rectangular plate of mass m, length of side adjacent to side containing axis of rotation is r(Axis of rotation along a side of the plate)		${displaystyle I={frac {1}{3}}mr^{2}}$
Solid rectangular cuboid of height h, width w, and depth d, and mass m. For a similarly oriented cube with sides of length $s$ , ${displaystyle I_{mathrm {CM} }={frac {1}{6}}ms^{2},!}$		${displaystyle I_{h}={frac {1}{12}}mleft(w^{2}+d^{2}right)}$ ${displaystyle I_{w}={frac {1}{12}}mleft(d^{2}+h^{2}right)}$ ${displaystyle I_{d}={frac {1}{12}}mleft(w^{2}+h^{2}right)}$
Solid cuboid of height D, width W, and length L, and mass m, rotating about the longest diagonal. For a cube with sides $s$ , ${displaystyle I={frac {1}{6}}ms^{2},!}$ .		${displaystyle I={frac {1}{6}}mleft({frac {W^{2}D^{2}+D^{2}L^{2}+W^{2}L^{2}}{W^{2}+D^{2}+L^{2}}}right)}$
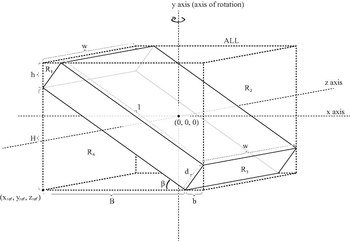
Tilted solid cuboid of depth d, width w, and length l, and mass m, rotating about the vertical axis (axis y as seen in figure). For a cube with sides $s$ , ${displaystyle I={frac {1}{6}}ms^{2},!}$ .		${displaystyle I={frac {m}{12}}left(l^{2}cos ^{2}beta +d^{2}sin ^{2}beta +w^{2}right)}$
Triangle with vertices at the origin and at P and Q, with mass m, rotating about an axis perpendicular to the plane and passing through the origin.		${displaystyle I={frac {1}{6}}m(mathbf {P} cdot mathbf {P} +mathbf {P} cdot mathbf {Q} +mathbf {Q} cdot mathbf {Q})}$
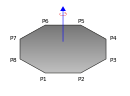
Plane polygon with vertices P₁, P₂, P₃,..., P_N and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.		${displaystyle I=mleft({frac {sum limits _{n=1}^{N}\|mathbf {P} _{n+1}times mathbf {P} _{n}\|left(left(mathbf {P} _{n}cdot mathbf {P} _{n}right)+left(mathbf {P} _{n}cdot mathbf {P} _{n+1}right)+left(mathbf {P} _{n+1}cdot mathbf {P} _{n+1}right)right)}{6sum limits _{n=1}^{N}\|mathbf {P} _{n+1}times mathbf {P} _{n}\|}}right)}$
Plane regular polygon with n-vertices and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through its barycenter. R is the radius of the circumscribed circle.		${displaystyle I={frac {1}{2}}mR^{2}left(1-{frac {2}{3}}sin ^{2}left({tfrac {pi }{n}}right)right)}$
An isosceles triangle of mass M, vertex angle 2β and common-side length L (axis through tip, perpendicular to plane)		${displaystyle I={frac {1}{2}}mL^{2}left(1-{frac {2}{3}}sin ^{2}left(beta right)right)}$
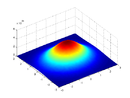
Infinite disk with mass distributed in a Bivariate Gaussian distribution on two axes around the axis of rotation with mass-density as a function of the position vector ${mathbf x}$ ${displaystyle rho ({mathbf {x} })=m{frac {exp left(-{frac {1}{2}}{mathbf {x} }^{mathrm {T} }{boldsymbol {Sigma }}^{-1}{mathbf {x} }right)}{sqrt {(2pi)^{2}\|{boldsymbol {Sigma }}\|}}}}$		${displaystyle I=mcdot operatorname {tr} ({boldsymbol {Sigma }}),!}$

Lista de tensores de inercia 3D

Esta lista de tensores de momento de inercia se proporciona para los ejes principales de cada objeto.

Para obtener los momentos de inercia escalares I anteriores, el momento de inercia tensorial I se proyecta a lo largo de algún eje definido por un vector unitario n > según la fórmula:

mathbf {n} cdot mathbf {I} cdot mathbf {n} equiv n_{i}I_{ij}n_{j},,

donde los puntos indican la contracción del tensor y se utiliza la convención de suma de Einstein. En la tabla anterior, n sería la unidad de base cartesiana e_x, e_y, e_z para obtener I_x, I_y, I_z respectivamente.

Descripción	Gráfico	Momento de tensor inercia
Esfera sólida de radio r y masa m		$I={begin{bmatrix}{frac {2}{5}}mr^{2}&0&0\0&{frac {2}{5}}mr^{2}&0\0&0&{frac {2}{5}}mr^{2}end{bmatrix}}$
Esfera hueca del radio r y masa m		$I={begin{bmatrix}{frac {2}{3}}mr^{2}&0&0\0&{frac {2}{3}}mr^{2}&0\0&0&{frac {2}{3}}mr^{2}end{bmatrix}}$
Elipsoide sólido de semi-axones a, b, c y masa m		$I={begin{bmatrix}{frac {1}{5}}m(b^{2}+c^{2})&0&0\0&{frac {1}{5}}m(a^{2}+c^{2})&0\0&0&{frac {1}{5}}m(a^{2}+b^{2})end{bmatrix}}$
Cono circular derecho con radio r, altura h y masa m, sobre el ápice		$I={begin{bmatrix}{frac {3}{5}}mh^{2}+{frac {3}{20}}mr^{2}&0&0\0&{frac {3}{5}}mh^{2}+{frac {3}{20}}mr^{2}&0\0&0&{frac {3}{10}}mr^{2}end{bmatrix}}$
Cuboide sólido de ancho w, altura h, profundidad d, y masa m	180x	$I={begin{bmatrix}{frac {1}{12}}m(h^{2}+d^{2})&0&0\0&{frac {1}{12}}m(w^{2}+d^{2})&0\0&0&{frac {1}{12}}m(w^{2}+h^{2})end{bmatrix}}$
Barra esbelta a lo largo Sí.-eje de longitud l y masa m sobre el final		$I={begin{bmatrix}{frac {1}{3}}ml^{2}&0&0\0&0&0\0&0&{frac {1}{3}}ml^{2}end{bmatrix}}$
Barra esbelta a lo largo Sí.-eje de longitud l y masa m sobre el centro		$I={begin{bmatrix}{frac {1}{12}}ml^{2}&0&0\0&0&0\0&0&{frac {1}{12}}ml^{2}end{bmatrix}}$
Cilindro sólido de radio r, altura h y masa m		$I={begin{bmatrix}{frac {1}{12}}m(3r^{2}+h^{2})&0&0\0&{frac {1}{12}}m(3r^{2}+h^{2})&0\0&0&{frac {1}{2}}mr^{2}end{bmatrix}}$
Tubo cilíndrico de paredes gruesas con extremos abiertos, de radio interior r₁, radio exterior r₂, longitud h y masa m		${displaystyle I={begin{bmatrix}{frac {1}{12}}m(3(r_{2}^{2}+r_{1}^{2})+h^{2})&0&0\0&{frac {1}{12}}m(3(r_{2}^{2}+r_{1}^{2})+h^{2})&0\0&0&{frac {1}{2}}m(r_{2}^{2}+r_{1}^{2})end{bmatrix}}}$

Contenido relacionado

Más resultados...