Lista de distribuciones de probabilidad

A muchas distribuciones de probabilidad que son importantes en teoría o aplicaciones se les han dado nombres específicos.

Distribuciones discretas

Con soporte finito

• La distribución Bernoulli, que toma el valor 1 con probabilidad p y valor 0 con probabilidad q 1 − p.
• La distribución Rademacher, que toma valor 1 con probabilidad 1/2 y valor −1 con probabilidad 1/2.
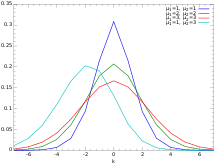
• La distribución binomial, que describe el número de éxitos en una serie de experimentos independientes Yes/No todos con la misma probabilidad de éxito.
• La distribución beta-binomial, que describe el número de éxitos en una serie de experimentos independientes Yes/No con heterogeneidad en la probabilidad de éxito.
• La distribución degenerada x₀, donde X es seguro tomar el valor x₀. Esto no parece aleatorio, pero satisface la definición de variable aleatoria. Esto es útil porque pone variables deterministas y variables aleatorias en el mismo formalismo.
• La distribución uniforme discreta, donde todos los elementos de un conjunto finito son igualmente probables. Este es el modelo de distribución teórica para una moneda equilibrada, una muerte imparcial, una ruleta de casino, o la primera carta de una cubierta bien doblada.
• La distribución hipergeométrica, que describe el número de éxitos en la primera m de una serie de n Sí consecutivo/No experimentos, si se conoce el número total de éxitos. Esta distribución surge cuando no hay reemplazo.
• La distribución hipergeométrica negativa, una distribución que describe el número de intentos necesarios para conseguir el nt éxito en una serie de experimentos Yes/No sin reemplazo.
• La distribución binomial Poisson, que describe el número de éxitos en una serie de experimentos independientes Yes/No con diferentes probabilidades de éxito.
• Distribución hipergeométrica no central de Fisher
• Distribución hipergeométrica no central de Wallenius
• La ley de Benford, que describe la frecuencia del primer dígito de muchos datos naturales.
• Las distribuciones soliton ideales y robustas.
• La ley de Zipf o la distribución de Zipf. Una distribución discreta de la ley de poder, cuyo ejemplo más famoso es la descripción de la frecuencia de las palabras en el idioma inglés.
• La ley Zipf-Mandelbrot es una distribución discreta de la ley de poder que es una generalización de la distribución de Zipf.

Con apoyo infinito

• Distribución binomial negativa beta
• La distribución Boltzmann, una distribución discreta importante en la física estadística que describe las probabilidades de los diversos niveles de energía discreta de un sistema en equilibrio térmico. Tiene una analogía continua. Los casos especiales incluyen:
  • Distribución de Gibbs
  • Distribución Maxwell-Boltzmann
• Distribución de Borel
• La distribución discreta del tipo de fase, una generalización de la distribución geométrica que describe la primera vez golpeada del estado absorbente de una cadena finita que termina Markov.
• Distribución binomial negativa ampliada
• Distribución generalizada de las series de registros
• Distribución Gauss–Kuzmin
• La distribución geométrica, una distribución discreta que describe el número de intentos necesarios para obtener el primer éxito en una serie de ensayos independientes de Bernoulli, o alternativamente sólo el número de pérdidas antes del primer éxito (es decir, uno menos).
• Distribución Hermite
• Distribución logarítmica (serie)
• Distribución de Poisson mixto
• Distribución binomial negativa o distribución pascal, generalización de la distribución geométrica a la néxito.
• Distribución del compuesto discreto Poisson
• Distribución fractal parabólica
• La distribución Poisson, que describe un número muy grande de eventos improbables individualmente que suceden en un intervalo de tiempo determinado. Relacionados con esta distribución son varias otras distribuciones: el Poisson desplazado, el hiper-Poisson, el binomial general Poisson y las distribuciones tipo Poisson.
  • La distribución Conway-Maxwell-Poisson, una extensión de dos parámetros de la distribución Poisson con una tasa ajustable de decadencia.
  • La distribución de Poisson sin tregua, para procesos en los que no se observan números cero
• Distribución Polya-Eggenberger
• La distribución de Skellam, la distribución de la diferencia entre dos variables aleatorias distribuidas por Poisson independientes.
• La distribución elíptica de la sierra
• Distribución Yule-Simon
• La distribución de zeta tiene usos en estadísticas aplicadas y mecánica estadística, y tal vez pueda ser de interés para los teóricos del número. Es la distribución Zipf para un número infinito de elementos.
• La distribución Hardy, que describe las probabilidades de las puntuaciones del agujero para un jugador de golf dado.

Distribuciones absolutamente continuas

Soportado en un intervalo acotado

• La distribución Beta en [0,1], una familia de distribuciones de dos parámetros con un modo, de los cuales la distribución uniforme es un caso especial, y que es útil para estimar las probabilidades de éxito.
  • Distribución Beta de cuatro parámetros, una generalización directa de la distribución Beta a intervalos arbitrarios consolidados [a,b]{displaystyle [a,b]}.
• La distribución arcsina en [a,b], que es un caso especial de la distribución Beta si α = β = 1/2, a = 0, y b = 1.
• La distribución PERT es un caso especial de la distribución beta de cuatro parámetros.
• Distribución uniforme o distribución rectangular en [a,b], donde todos los puntos en un intervalo finito son igualmente probables, es un caso especial de la distribución Beta de cuatro parámetros.
• La distribución Irwin-Hall es la distribución de la suma de la n variables aleatorias independientes, cada una de las cuales tiene la distribución uniforme en [0,1].
• La distribución de los Bates es la distribución de la media n variables aleatorias independientes, cada una de las cuales tiene la distribución uniforme en [0,1].
• La distribución logit-normal en (0,1).
• La función Dirac delta, aunque no estrictamente una distribución de probabilidad, es una forma de limitación de muchas funciones de probabilidad continua. Representa una discreta distribución de probabilidad concentrada en 0 —una distribución degenerada— es una Distribución (matemática) en el sentido generalizado de la función; pero la notación lo trata como si fuera una distribución continua.
• La distribución de Kent en la esfera bidimensional.
• La distribución Kumaraswamy es tan versátil como la distribución Beta pero tiene formas simples cerradas tanto para el cdf como para el pdf.
• La distribución logit metalog, que es altamente flexible en forma, tiene formas simples cerradas, y puede ser parametizada con datos usando mínimos cuadrados lineales.
• La distribución Marchenko-Pastur es importante en la teoría de matrices aleatorias.
• Las distribuciones parametrizadas cuantitativas, altamente flexibles y pueden ser parametizadas con datos usando mínimos cuadrados lineales (véase distribución parametrizada cuantitativa#Transformaciones)
• Distribución cosina elevada en [μ μ − − s,μ μ +s{displaystyle mu -s,mu +s}]
• Distribución recíproca
• La distribución triangular en [a, b], un caso especial de que es la distribución de la suma de dos variables aleatorias distribuidas uniformemente independientes (la convolution de dos distribuciones uniformes).
• Distribución trapezoidal
• La distribución normal truncada en [a, b].
• Distribución U-quadratic en [a, b].
• La distribución de Von Mises-Fisher en N-dimensional esfera tiene la distribución de von Mises como un caso especial.
• La distribución de Bingham en N- esfera dimensional.
• La distribución de semicírculos Wigner es importante en la teoría de matrices aleatorias.
• La distribución continua de Bernoulli es una familia exponencial de un solo parámetro que proporciona una contraparte probabilística a la pérdida binaria de la entropía.

Soportado en intervalos de longitud 2π – distribuciones direccionales

• Función de fase Henyey-Greenstein
• Función de la fase Mie
• Distribución de von Mises
• La distribución normal envuelta
• La distribución exponencial envuelta
• La distribución envuelta de Lévy
• La distribución de Cauchy envuelta
• La distribución de Laplace envuelta
• Distribución envuelta asimétrica de Laplace
• El peine Dirac del período 2π, aunque no estrictamente una función, es una forma límite de muchas distribuciones direccionales. Es esencialmente una función Dirac delta envuelta. Representa una discreta distribución de la probabilidad concentrada en 2πn — una distribución degenerada — pero la notación lo trata como si fuera una distribución continua.

Admitido en intervalos semiinfinitos, normalmente [0,∞)

• La distribución principal de Beta
• La distribución Birnbaum-Saunders, también conocida como la distribución de la vida de fatiga, es una distribución de probabilidad utilizada ampliamente en aplicaciones de confiabilidad a tiempos de falla modelo.
• La distribución chi
  • Distribución de chi no central
• La distribución chi-cuadrada, que es la suma de los cuadrados de n variables independientes Gaussian random. Es un caso especial de la distribución Gamma, y se utiliza en pruebas de bondad de beneficio en las estadísticas.
  • Distribución inversa-chi-squared
  • La distribución no central de chi-squared
  • La distribución inversa de chi-squared
• Distribución Dagum
• La distribución exponencial, que describe el tiempo entre eventos aleatorios raros consecutivos en un proceso sin memoria.
• Distribución exponencial-logarítmica
• La F-distribución, que es la distribución de la relación de dos (normalizadas) variables aleatorias distribuidas en chi-squared, utilizadas en el análisis de la varianza. Se conoce como la distribución principal beta cuando es la proporción de dos variatos quiscuas que no se normalizan dividiéndolos por su número de grados de libertad.
  • La distribución F no central
• La distribución normal plegada
• Distribución de Fréchet
• La distribución Gamma, que describe el tiempo hasta n eventos aleatorios consecutivos raros ocurren en un proceso sin memoria.
  • La distribución Erlang, que es un caso especial de la distribución gamma con parámetro de forma integral, desarrollada para predecir los tiempos de espera en los sistemas de búsqueda
  • Distribución inversa-gamma
• Distribución gamma generalizada
• Distribución generalizada de Pareto
• Distribución Gamma/Gompertz
• La distribución Gompertz
• La distribución medio-normal
• Distribución de la T de Hotelling
• La distribución inversa de Gaussian, también conocida como la distribución Wald
• Distribución de Lévy
• Distribución log-Cauchy
• Distribución log-Laplace
• Distribución logística
• La distribución log-metalog, que es altamente flexil de forma, tiene formas simples cerradas, se puede parametizar con datos utilizando mínimos cuadrados lineales, y sustituye la distribución log-logistic como caso especial.
• La distribución log-normal, describiendo variables que pueden ser modeladas como el producto de muchas pequeñas variables positivas independientes.
• La distribución Lomax
• Distribución Mittag-Leffler
• Distribución Nakagami
• La distribución de Pareto, o distribución de "ley de poder", utilizado en el análisis de datos financieros y comportamiento crítico.
• Distribución Pearson Tipo III
• La distribución tipo fase, utilizada en la teoría de colas
• La distribución bi-exponencial gradual se utiliza comúnmente en farmacocinética
• Distribución gradual bi-Weibull
• Las distribuciones semifinalizadas, altamente flexibles en forma y pueden ser parametizadas con datos usando mínimos cuadrados lineales (véase distribución cuantitativa parametrizada § Transformaciones
• Distribución de Rayleigh
• Distribución de la mezcla Rayleigh
• Distribución del arroz
• La distribución de Gompertz cambiada
• Distribución Gumbel tipo-2
• La distribución Weibull o la distribución de Rosin Rammler, de la que la distribución exponencial es un caso especial, se utiliza para modelar la vida útil de los dispositivos técnicos y se utiliza para describir la distribución del tamaño de partículas generadas por las operaciones de trituración, fresado y trituración.
• La distribución media-normal modificada.
• Distribución Polya-Gamma
• La distribución modificada Polya-gamma.

Soportado en toda la línea real

• La distribución Behrens-Fisher, que surge en el problema Behrens-Fisher.
• La distribución Cauchy, un ejemplo de una distribución que no tiene un valor esperado o una varianza. En física generalmente se llama perfil Lorentziano, y está asociado con muchos procesos, incluyendo la resonancia de distribución de energía, impacto y la línea espectral natural ampliando y ampliando la línea de Stark cuadrática.
• La distribución inversa-Fano centralizada, que es la distribución que representa la relación de variables aleatorias normales independientes y gamma-diferencia.
• Distribución de Chernoff
• La distribución exponencialmente modificada Gaussiana, una convolución de una distribución normal con una distribución exponencial, y la distribución exponencial menos gausiana, una convolución de una distribución normal con el negativo de una distribución exponencial.
• La distribución de expectiles, que anida la distribución Gaussiana en el caso simétrico.
• La distribución Fisher-Tippett, valor extremo o log-Weibull
• Fisher z-distribución
• La distribución generalizada de t
• La distribución gamma-difference, que es la distribución de la diferencia de variables gamma aleatorias independientes.
• Distribución logística generalizada
• Distribución normal generalizada
• La distribución geométrica estable
• Distribución Gumbel
• La distribución Holtsmark, un ejemplo de una distribución que tiene un valor esperado finito pero varianza infinita.
• Distribución hiperbólica
• Distribución del secant hiperbólico
• Distribución de Johnson SU
• Distribución de Landau
• Distribución del lugar
• La distribución alfa-estable de Lévy es una familia de distribuciones que a menudo se utilizan para caracterizar datos financieros y comportamientos críticos; la distribución Cauchy, distribución Holtsmark, distribución Landau, distribución Lévy y distribución normal son casos especiales.
• Distribución Linnik
• Distribución logística
• La distribución del mapa-Airy
• La distribución de metalog, que es altamente flexible en forma, tiene formas simples cerradas, y puede ser parametizada con datos usando mínimos cuadrados lineales.
• La distribución normal, también llamada Gaussian o la curva de campana. Es omnipresente en la naturaleza y las estadísticas debido al teorema límite central: cada variable que puede ser modelada como una suma de muchas pequeñas variables independientes, distribuidas idénticamente con media finita y varianza es aproximadamente normal.
• Distribución de la gamma-exponencial normal
• Distribución Gaussiana normal
• Distribución Pearson Tipo IV (ver distribuciones Pearson)
• Las distribuciones cuantil-parametrizadas, que son altamente flexibles en forma y pueden ser parametizadas con datos usando mínimos cuadrados lineales.
• La distribución normal del tirón
• La t-distribución del estudiante, útil para estimar medios desconocidos de poblaciones gausianas.
  • La distribución no central
  • La distribución de la moto t
• Distribución Champernowne
• Distribución Gumbel tipo-1
• Distribución Tracy-Widom
• La distribución Voigt, o perfil Voigt, es la evolución de una distribución normal y una distribución Cauchy. Se encuentra en espectroscopia cuando los perfiles de línea espectral se amplían mediante una mezcla de mecanismos de ampliación Lorentzian y Doppler.
• La distribución de Chen.

Con soporte variable

• La distribución generalizada de valor extremo tiene un límite superior finito o un límite inferior finito dependiendo de qué rango se encuentra el valor de uno de los parámetros de la distribución (o se apoya en toda la línea real para un valor especial del parámetro
• La distribución generalizada de Pareto cuenta con un apoyo que se limita sólo a continuación, o que se limita tanto arriba como abajo
• La distribución de metalog, que proporciona flexibilidad para el soporte sin límites, ligado y semi-limitado, es altamente flexible en forma, tiene formas simples cerradas, y puede ajustarse a los datos usando mínimos cuadrados lineales.
• La distribución de lambda Tukey está soportada en toda la línea real, o en un intervalo atado, dependiendo de qué rango se encuentre el valor de uno de los parámetros de la distribución.
• Distribución de Wakeby

Distribuciones mixtas discretas/continuas

• La distribución Gaussiana rectificada reemplaza valores negativos de una distribución normal con un componente discreto a cero.
• La distribución compuesta poisson-gamma o Tweedie es continua sobre los números reales estrictamente positivos, con una masa a cero.

Distribuciones conjuntas

Para cualquier conjunto de variables aleatorias independientes, la función de densidad de probabilidad de su distribución conjunta es el producto de sus funciones de densidad individuales.

Dos o más variables aleatorias en el mismo espacio muestral

• La distribución Dirichlet, una generalización de la distribución beta.
• La fórmula de muestreo de Ewens es una distribución de probabilidad en el conjunto de todas las particiones de un entero n, surgiendo en genética poblacional.
• El modelo Balding-Nichols
• La distribución multinomial, una generalización de la distribución binomial.
• La distribución normal multivariada, una generalización de la distribución normal.
• La distribución multivariada t, una generalización de la distribución t del estudiante.
• La distribución multinomial negativa, una generalización de la distribución binomial negativa.
• La distribución multinomial negativa Dirichlet, una generalización de la distribución binomial negativa beta.
• Distribución multivariada de log-gamma
• Distribución exponencial de Marshall-Olkin
• La distribución continua-categorical, una familia exponencial apoyada en el simplex que generaliza la distribución continua de Bernoulli.

Distribuciones de variables aleatorias matriciales

• Distribución de Wishart
• Distribución inversa-Wishart
• Distribución Lewandowski-Kurowicka-Joe
• Distribución normal de la matriz
• La matriz t-distribución
• Distribución Matrix Langevin
• La matriz variate beta distribution

Distribuciones no numéricas

• Distribución categórica

Distribuciones varias

• Distribución Cantor
• La familia de distribución logística generalizada
• La familia de distribución de metalog
• La familia de distribución Pearson
• Distribución tipo fase