Línea de transmisión

Esquema de una onda que se mueve hacia la derecha hacia abajo una línea de transmisión sin pérdidas de dos hilos. Los puntos negros representan electrones, y las flechas muestran el campo eléctrico.

Uno de los tipos más comunes de línea de transmisión, cable coaxial.

En ingeniería eléctrica, una línea de transmisión es un cable especializado u otra estructura diseñada para conducir ondas electromagnéticas de forma contenida. El término se aplica cuando los conductores son lo suficientemente largos como para tener en cuenta la naturaleza ondulatoria de la transmisión. Esto se aplica especialmente a la ingeniería de radiofrecuencia porque las longitudes de onda cortas significan que los fenómenos ondulatorios surgen en distancias muy cortas (esto puede ser tan corto como milímetros dependiendo de la frecuencia). Sin embargo, la teoría de las líneas de transmisión se desarrolló históricamente para explicar fenómenos en líneas telegráficas muy largas, especialmente cables telegráficos submarinos.

Las líneas de transmisión se utilizan para fines tales como conectar transmisores y receptores de radio con sus antenas (entonces se denominan líneas de alimentación o alimentadores), distribuir señales de televisión por cable, líneas troncales que enrutan llamadas entre centros de conmutación telefónica, conexiones de redes informáticas y computadoras de alta velocidad. buses de datos Los ingenieros de RF suelen utilizar piezas cortas de línea de transmisión, generalmente en forma de líneas de transmisión planas impresas, dispuestas en ciertos patrones para construir circuitos como filtros. Estos circuitos, conocidos como circuitos de elementos distribuidos, son una alternativa a los circuitos tradicionales que utilizan capacitores e inductores discretos.

Resumen

Los cables eléctricos ordinarios son suficientes para transportar corriente alterna (CA) de baja frecuencia, como la red eléctrica, que invierte la dirección de 100 a 120 veces por segundo, y señales de audio. Sin embargo, no se pueden utilizar para transportar corrientes en el rango de radiofrecuencia, por encima de unos 30 kHz, porque la energía tiende a irradiarse del cable en forma de ondas de radio, lo que provoca pérdidas de potencia. Las corrientes de radiofrecuencia también tienden a reflejarse en las discontinuidades del cable, como conectores y empalmes, y viajan de regreso por el cable hacia la fuente. Estos reflejos actúan como cuellos de botella, impidiendo que la potencia de la señal llegue al destino. Las líneas de transmisión utilizan una construcción especializada y adaptación de impedancia para transportar señales electromagnéticas con reflejos y pérdidas de energía mínimos. La característica distintiva de la mayoría de las líneas de transmisión es que tienen dimensiones de sección transversal uniformes a lo largo de su longitud, lo que les otorga una impedancia uniforme, denominada impedancia característica, para evitar reflejos. Los tipos de línea de transmisión incluyen línea paralela (línea de escalera, par trenzado), cable coaxial y líneas de transmisión planas, como línea de banda y microbanda. Cuanto mayor sea la frecuencia de las ondas electromagnéticas que se mueven a través de un cable o medio determinado, menor será la longitud de onda de las ondas. Las líneas de transmisión se vuelven necesarias cuando la longitud de onda de la frecuencia transmitida es lo suficientemente corta como para que la longitud del cable se convierta en una parte importante de una longitud de onda.

A frecuencias de microondas y superiores, las pérdidas de energía en las líneas de transmisión se vuelven excesivas y, en su lugar, se utilizan guías de ondas, que funcionan como "tuberías" para confinar y guiar las ondas electromagnéticas. Algunas fuentes definen las guías de ondas como un tipo de línea de transmisión; sin embargo, este artículo no los incluirá. A frecuencias aún más altas, en los rangos de terahercios, infrarrojos y visibles, las guías de ondas a su vez se vuelven con pérdidas y se utilizan métodos ópticos (como lentes y espejos) para guiar las ondas electromagnéticas.

Historia

El análisis matemático del comportamiento de las líneas de transmisión eléctrica surgió del trabajo de James Clerk Maxwell, Lord Kelvin y Oliver Heaviside. En 1855, Lord Kelvin formuló un modelo de difusión de la corriente en un cable submarino. El modelo predijo correctamente el bajo rendimiento del cable telegráfico submarino transatlántico de 1858. En 1885, Heaviside publicó los primeros artículos que describían su análisis de la propagación en cables y la forma moderna de las ecuaciones del telegrafista.

El modelo de cuatro terminales

Variaciones en el símbolo electrónico esquemático para una línea de transmisión.

Para fines de análisis, una línea de transmisión eléctrica se puede modelar como una red de dos puertos (también llamada cuadripolo), de la siguiente manera:

En el caso más simple, se supone que la red es lineal (es decir, el voltaje complejo a través de cualquiera de los puertos es proporcional a la corriente compleja que fluye hacia él cuando no hay reflejos), y se supone que los dos puertos son intercambiables. Si la línea de transmisión es uniforme a lo largo de su longitud, entonces su comportamiento se describe en gran medida por un solo parámetro llamado impedancia característica, símbolo Z₀. Esta es la relación entre el voltaje complejo de una onda dada y la corriente compleja de la misma onda en cualquier punto de la línea. Los valores típicos de Z₀ son 50 o 75 ohmios para un cable coaxial, alrededor de 100 ohmios para un par trenzado de cables y alrededor de 300 ohmios para un tipo común de par no trenzado que se usa en la transmisión de radio.

Al enviar energía a través de una línea de transmisión, generalmente es deseable que la carga absorba la mayor cantidad posible de energía y que la menor cantidad posible se refleje hacia la fuente. Esto se puede asegurar haciendo que la impedancia de carga sea igual a Z₀, en cuyo caso se dice que la línea de transmisión está coincidente.

Una línea de transmisión se dibuja como dos alambres negros. A una distancia x en la línea, hay corriente I(x) viajar a través de cada alambre, y hay una diferencia de tensión V(x) entre los cables. Si la corriente y el voltaje provienen de una sola onda (sin reflexión), entonces V()x)I()x)Z₀, donde Z₀ es impedancia característica de la línea.

Parte de la energía que alimenta una línea de transmisión se pierde debido a su resistencia. Este efecto se llama pérdida óhmica o resistiva (ver calentamiento óhmico). A altas frecuencias, otro efecto llamado pérdida dieléctrica se vuelve significativo y se suma a las pérdidas causadas por la resistencia. La pérdida dieléctrica se produce cuando el material aislante dentro de la línea de transmisión absorbe energía del campo eléctrico alterno y la convierte en calor (ver calentamiento dieléctrico). La línea de transmisión se modela con una resistencia (R) y una inductancia (L) en serie con una capacitancia (C) y una conductancia (G) en paralelo. La resistencia y la conductancia contribuyen a la pérdida en una línea de transmisión.

La pérdida total de potencia en una línea de transmisión a menudo se especifica en decibelios por metro (dB/m) y, por lo general, depende de la frecuencia de la señal. El fabricante a menudo proporciona un gráfico que muestra la pérdida en dB/m en un rango de frecuencias. Una pérdida de 3 dB corresponde aproximadamente a la mitad de la potencia.

Las líneas de transmisión de alta frecuencia se pueden definir como aquellas diseñadas para transportar ondas electromagnéticas cuyas longitudes de onda son más cortas o comparables a la longitud de la línea. En estas condiciones, las aproximaciones útiles para los cálculos a frecuencias más bajas ya no son precisas. Esto ocurre a menudo con señales ópticas, de microondas y de radio, filtros ópticos de malla metálica y con las señales que se encuentran en los circuitos digitales de alta velocidad.

Ecuaciones del telegrafista

El ecuaciones de telégrafo (o simplemente ecuaciones de telégrafo) son un par de ecuaciones diferenciales lineales que describen el voltaje (V{displaystyle V}) y actual (I{displaystyle Yo...) en una línea de transmisión eléctrica con distancia y tiempo. Ellos fueron desarrollados por Oliver Heaviside que creó el modelo de línea de transmisiónY están basados en las ecuaciones de Maxwell.

Representación esquemática del componente elemental de una línea de transmisión.

El modelo de línea de transmisión es un ejemplo del modelo de elementos distribuidos. Representa la línea de transmisión como una serie infinita de componentes elementales de dos puertos, cada uno de los cuales representa un segmento infinitesimalmente corto de la línea de transmisión:

• Resistencia distribuida R{displaystyle R. de los conductores está representado por un resistor de serie (expresado en ohms por longitud de unidad).
• La inductancia distribuida L{displaystyle L. (debido al campo magnético alrededor de los alambres, auto-inductancia, etc.) está representado por un ductor de serie (en las heces por longitud de unidad).
• La capacitancia C{displaystyle C} entre los dos conductores está representado por un condensador shunt (en farads por longitud de unidad).
• La conducta G{displaystyle G. del material dieléctrico que separa a los dos conductores está representado por un resistor de punta entre el alambre de señal y el alambre de retorno (en siemens por longitud de unidad).

El modelo consiste en un serie infinita de los elementos mostrados en la figura, y los valores de los componentes se especifican por unidad para que la imagen del componente pueda ser engañosa. R{displaystyle R., L{displaystyle L., C{displaystyle C}, y G{displaystyle G. puede ser también funciones de frecuencia. Una notación alternativa es usar R.{displaystyle R}, L.{displaystyle Yo..., C.{displaystyle C'} y G.{displaystyle G. enfatizar que los valores son derivados con respecto a la longitud. Estas cantidades también pueden ser conocidas como las constantes de la línea primaria para distinguir de las constantes de la línea secundaria derivadas de ellas, siendo ésta la constante de propagación, constante de atenuación y constante de fase.

Tensión de línea V()x){displaystyle V(x)} y la corriente I()x){displaystyle I(x)} se puede expresar en el dominio de frecuencia como

∂ ∂ V()x)∂ ∂ x=− − ()R+j⋅ ⋅ L)I()x){displaystyle {frac {partial V(x)}{partial x}=-(R+j,omega ,L),I(x)}

∂ ∂ I()x)∂ ∂ x=− − ()G+j⋅ ⋅ C)V()x).{displaystyle {frac {partial I(x)}{partial x}=-(G+j,omega ,C),V(x)~,}

(ver ecuación diferencial, frecuencia angular ω y unidad imaginaria j)

Caso especial de una línea sin pérdidas

Cuando los elementos R{displaystyle R. y G{displaystyle G. son insignificantes la línea de transmisión se considera una estructura sin pérdidas. En este caso hipotético, el modelo depende sólo del L{displaystyle L. y C{displaystyle C} elementos que simplifican enormemente el análisis. Para una línea de transmisión sin pérdidas, las ecuaciones de Telegrapher de segundo orden son:

∂ ∂ 2V()x)∂ ∂ x2+⋅ ⋅ 2LCV()x)=0{displaystyle {frac {partial ^{2}V(x)}{partial x^{2}}+omega ^{2}L,C,V(x)=0}

∂ ∂ 2I()x)∂ ∂ x2+⋅ ⋅ 2LCI()x)=0.{displaystyle {frac {partial }I(x)}{partial x^{2}}+omega ^{2}L,C,I(x)=0~,}

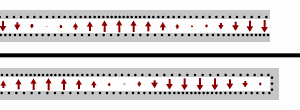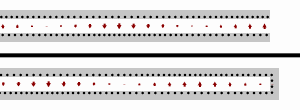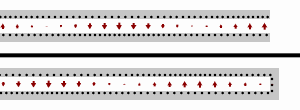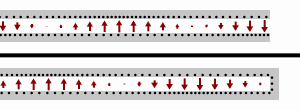
Estas son ecuaciones de onda que tienen ondas planas con la misma velocidad de propagación en las direcciones directa e inversa como soluciones. El significado físico de esto es que las ondas electromagnéticas se propagan por las líneas de transmisión y, en general, hay un componente reflejado que interfiere con la señal original. Estas ecuaciones son fundamentales para la teoría de líneas de transmisión.

Caso general de una línea con pérdidas

En el caso general los términos de pérdida, R{displaystyle R. y G{displaystyle G., ambos están incluidos, y la forma completa de las ecuaciones del Telegrapher se convierten en:

∂ ∂ 2V()x)∂ ∂ x2=γ γ 2V()x){displaystyle {frac {partial ^{2}V(x)}{partial x^{2}}=gamma ^{2}V(x),}

∂ ∂ 2I()x)∂ ∂ x2=γ γ 2I()x){displaystyle {frac {partial }I(x)}{partial x^{2}=gamma ^{2}I(x),}

Donde γ γ {displaystyle gamma } es la constante de propagación (complejo). Estas ecuaciones son fundamentales para la teoría de la línea de transmisión. También son ecuaciones de onda, y tienen soluciones similares al caso especial, pero que son una mezcla de pecados y cosines con factores de decaimiento exponencial. Solving for the propagation constant γ γ {displaystyle gamma } en términos de los parámetros primarios R{displaystyle R., L{displaystyle L., G{displaystyle G., y C{displaystyle C} da:

γ γ =()R+j⋅ ⋅ L)()G+j⋅ ⋅ C){displaystyle gamma ={sqrt {(R+j,omega ,L)(G+j,omega ,C),}}}}

y la impedancia característica se puede expresar como

Z0=R+j⋅ ⋅ LG+j⋅ ⋅ C.{displaystyle Z_{0}={sqrt {frac {R+j,omega ,L}{G+j,omega ,C},}~,}

Las soluciones para V()x){displaystyle V(x)} y I()x){displaystyle I(x)} son:

V()x)=V()+)e− − γ γ x+V()− − )e+γ γ x{displaystyle V(x)=V_{(+)}e^{-gamma ,x}+V_{(-)}e^{+gamma #

I()x)=1Z0()V()+)e− − γ γ x− − V()− − )e+γ γ x).{displaystyle I(x)={frac {1}{Z_{0},left(V_{(+)}e^{-gamma ,x}-V_{(-)}e^{+gamma ,x}right)~,}

Las constantes V()± ± ){displaystyle V_{(pm)} debe determinarse desde las condiciones fronterizas. Para un pulso de tensión Vin()t){displaystyle V_{mathrm}(t),}, comenzando en x=0{displaystyle x=0} y moverse en el positivo x{displaystyle x}dirección, luego el pulso transmitido Vout()x,t){displaystyle V_{mathrm}(x,t),} en posición x{displaystyle x} puede obtenerse computando el Fourier Transform, V~ ~ ()⋅ ⋅ ){displaystyle {tilde {V}(omega)}, de Vin()t){displaystyle V_{mathrm}(t),}, atenuando cada componente de frecuencia por e− − Re⁡ ⁡ ()γ γ )x{displaystyle e^{-fnMimbre de operador {Re} (gamma),x},}, avanzando su fase por − − Im⁡ ⁡ ()γ γ )x{displaystyle -operatorname {Im} (gamma),x,}, y tomar el inverso Fourier Transform. Las partes reales e imaginarias de γ γ {displaystyle gamma } puede ser calculado como

Re⁡ ⁡ ()γ γ )=α α =()a2+b2)1/4#⁡ ⁡ ()↑ ↑ ){displaystyle operatorname {Re} (gamma)=alpha =(a^{2}+b^{2})^{1/4}cos(psi)}

Im⁡ ⁡ ()γ γ )=β β =()a2+b2)1/4pecado⁡ ⁡ ()↑ ↑ ){displaystyle operatorname {Im} (gamma)=beta =(a^{2}+b^{2})^{1/4}sin(psi),}

con

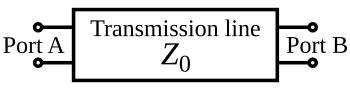
a↑ ↑ RG− − ⋅ ⋅ 2LC=⋅ ⋅ 2LC[()R⋅ ⋅ L)()G⋅ ⋅ C)− − 1]{fnMiequipo a~equiv ~R,G,-omega ^{2}L,C ~=~omega ^{2}L,C,left[left({frac {f}{omega L}right)left({frac}{omega C}}right)-1}

b↑ ↑ ⋅ ⋅ CR+⋅ ⋅ LG=⋅ ⋅ 2LC()R⋅ ⋅ L+G⋅ ⋅ C){displaystyle b~equiv ~omega ,C,R+omega ,L,G~=~omega ^{2}L,C,left({frac {R}{omega ,L}}+{frac {G}{omega ,C}right)}

las expresiones de la mano derecha que sostienen cuando ni L{displaystyle L., ni C{displaystyle C}, ni ⋅ ⋅ {displaystyle omega } es cero, y con

↑ ↑ ↑ ↑ 12atan2⁡ ⁡ ()b,a){displaystyle psi ~equiv ~{tfrac [1}{2}operatorname {atan2} (b,a),}

donde atan2 es la forma definida en todas partes de la función arcotangente de dos parámetros, con valor arbitrario cero cuando ambos argumentos son cero.

Alternativamente, la raíz cuadrada compleja se puede evaluar algebraicamente para producir:

α α =± ± b2()− − a+a2+b2),{displaystyle alpha ={frac {fnK}{sqrt {2left(-a+{sqrt {a}+b^{2}} {}}}}}}}}}}

y

β β =± ± 12()− − a+a2+b2),{displaystyle beta =pm {{tfrac {1}{2}left(-a+{sqrt {a^{2}+b^{2}} {}}}}}}}}}}}

con el más o menos signos escogidos opuestos a la dirección del movimiento de la ola a través del medio conductor. (Nota eso) a es generalmente negativo, ya G{displaystyle G. y R{displaystyle R. son generalmente mucho más pequeños que ⋅ ⋅ C{displaystyle omega C} y ⋅ ⋅ L{displaystyle omega L}, respectivamente, así −a es generalmente positivo. b es siempre positivo.)

Caso especial de baja pérdida

Para pequeñas pérdidas y altas frecuencias, las ecuaciones generales se pueden simplificar: Si R⋅ ⋅ L≪ ≪ 1{displaystyle {tfrac {R}{omega ,L}ll 1} y G⋅ ⋅ C≪ ≪ 1{displaystyle {tfrac {}{omega ,C}ll 1} entonces

Re⁡ ⁡ ()γ γ )=α α .. 12LC()RL+GC){displaystyle operatorname {Re} (gamma)=alpha approx {tfrac {1}{2}{sqrt {L,C,}},left({fracfracfnMicroc} {fnMicroc}} {fnMicroc}}cccH0}ccH0}cccH00ccccH00cH00ccccH00cH00cH00ccH00cH00cH00cH00cH00cH00cccH00cH00cH00cH00cH00ccH00cH00cH00cH00cH00}cH00}cH00cH00cH00}cH00cH00cH00}ccH00c {R} {L}}+{frac {G} {C}right),}

Im⁡ ⁡ ()γ γ )=β β .. ⋅ ⋅ LC.{displaystyle operatorname {Im} (gamma)=beta approx omega ,{sqrt {L,C,}~,}

Desde un avance en fase por − − ⋅ ⋅ δ δ {displaystyle -omega ,delta } equivale a una demora de tiempo por δ δ {displaystyle delta }, Vout()t){displaystyle V_{out}(t)} puede ser simplemente calculado como

Vout()x,t).. Vin()t− − LCx)e− − 12LC()RL+GC)x.{displaystyle V_{mathrm {out}(x,t)approx V_{mathrm {in}(t-{sqrt {L,C,},x),e^{-{tfrac {1}{2}{sqrt {L,C,},left({fracfnMic {R}}+{frac {C}derecha),x}

Condición de Heaviside

La condición de Heaviside es un caso especial en el que la onda viaja a lo largo de la línea sin ninguna distorsión de dispersión. La condición para que esto suceda es

GC=RL{displaystyle {frac {f} {fnMicroc} {fnMicroc}}}} {fnMicroc} {fn}}}}} {fnMicroc}}}} {fnMicroc}}}}} {fnMicroc} {R} {L}}

Impedancia de entrada de la línea de transmisión

Mirando hacia una carga a través de una longitud l l {displaystyle ell } de la línea de transmisión sin pérdida, la impedancia cambia como l l {displaystyle ell } aumenta, siguiendo el círculo azul en este gráfico de impedancia Smith. (Esta impedancia se caracteriza por su coeficiente de reflexión, que es el voltaje reflejado dividido por el voltaje del incidente.) El círculo azul, centrado en el gráfico, a veces se llama un SWR circle (Corto para constante de onda de pie).

La impedancia característica Z0{displaystyle Z_{0} de una línea de transmisión es la relación de la amplitud de una single onda de voltaje a su onda actual. Como la mayoría de las líneas de transmisión también tienen una onda reflejada, la impedancia característica generalmente no es la impedancia que se mide en la línea.

La impedancia medida a cierta distancia l l {displaystyle ell } de la impedancia de carga ZL{displaystyle Z_{mathrm {L}} puede expresarse como

Zin()l l )=V()l l )I()l l )=Z01+.. Le− − 2γ γ l l 1− − .. Le− − 2γ γ l l {displaystyle Z_{mathrm}left(ell right)={frac {V(ell)}{I(ell)}}=Z_{0}{frac {1+{mit} {fnMicrosoft Sans Serif} {L}e^{-2gamma ell }{1-{ mathit {fnMicrosoft Sans Serif} {L}e^{-2gammaell}}},

Donde γ γ {displaystyle gamma } es la propagación constante y .. L=ZL− − Z0ZL+Z0{fnMitit {fnMitit {fnMicrosoft Sans Serif} {L}={frac {fnMicroc} {L}-Z_{0},}{Z_{mathrm {L}+Z_{0}}} es el coeficiente de reflexión de voltaje medido en el extremo de carga de la línea de transmisión. Alternativamente, la fórmula anterior se puede reorganizar para expresar la impedancia de entrada en términos de impedancia de carga en lugar del coeficiente de reflexión de voltaje de carga:

Zin()l l )=Z0ZL+Z0Tanh⁡ ⁡ ()γ γ l l )Z0+ZLTanh⁡ ⁡ ()γ γ l l ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {L} }+Z_{0}tanh left(gamma ell right)}{Z_{0}+Z_{mathrm {L},tanh left(gamma ell right)}}}}}}.

Impedancia de entrada de la línea de transmisión sin pérdidas

Para una línea de transmisión sin pérdidas, la constante de propagación es puramente imaginaria, γ γ =jβ β {displaystyle gamma =j,beta }, por lo que las fórmulas anteriores pueden ser reescritas como

Zin()l l )=Z0ZL+jZ0#⁡ ⁡ ()β β l l )Z0+jZL#⁡ ⁡ ()β β l l ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {L} }+j,Z_{0},tan(beta ell)}{Z_{0}+j,Z_{mathrm {L}tan(beta ell)}}}}}

Donde β β =2π π λ λ {displaystyle beta ={frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} } es el número de onda.

Al calcular β β ,{displaystyle beta} la longitud de onda es generalmente diferente dentro la línea de transmisión a lo que sería en el espacio libre. En consecuencia, el factor de velocidad del material que la línea de transmisión se hace de las necesidades a tener en cuenta al realizar dicho cálculo.

Casos especiales de líneas de transmisión sin pérdidas

Media longitud de onda

Para el caso especial donde β β l l =nπ π {displaystyle beta ,ell =n,pi} donde n es un entero (que significa que la longitud de la línea es un múltiplo de media longitud de onda), la expresión reduce a la impedancia de carga para que

Zin=ZL{displaystyle Z_{mathrm {in} }=Z_{mathrm {L},}

para todos n.{displaystyle n,} Esto incluye el caso cuando n=0{displaystyle n=0}, lo que significa que la longitud de la línea de transmisión es insignificante en comparación con la longitud de onda. El significado físico de esto es que la línea de transmisión puede ser ignorada (es decir, tratada como un alambre) en cualquier caso.

Longitud de un cuarto de onda

Para el caso en que la longitud de la línea sea un cuarto de longitud de onda, o un múltiplo impar de un cuarto de longitud de onda, la impedancia de entrada se convierte en

Zin=Z02ZL.{displaystyle Z_{mathrm {in} }={frac {Z_{0}{2}{Z_{mathrm.

Carga combinada

Otro caso especial es cuando la impedancia de carga es igual a la impedancia característica de la línea (es decir, la línea coincide), en cuyo caso la impedancia se reduce a la impedancia característica de la línea de modo que

Zin=ZL=Z0{displaystyle Z_{mathrm {in} }=Z_{mathrm {L}=Z_{0},}

para todos l l {displaystyle ell } y todos λ λ {displaystyle lambda }.

Corto

Las ondas permanentes en una línea de transmisión con una carga de circuito abierto (top), y una carga de cortocircuito (bottom). Los puntos negros representan electrones, y las flechas muestran el campo eléctrico.

Para el caso de una carga cortada (es decir, ZL=0{displaystyle Z_{mathrm {L}=0}), la impedancia de entrada es puramente imaginaria y una función periódica de posición y longitud de onda (frecuencia)

Zin()l l )=jZ0#⁡ ⁡ ()β β l l ).{displaystyle Z_{mathrm {in}(ell)=j,Z_{0},tan(beta ell).,}

Abierto

Para el caso de una carga abierta (es decir, ZL=JUEGO JUEGO {displaystyle Z_{mathrm {L}=infty), la impedancia de entrada es una vez más imaginario y periódico

Zin()l l )=− − jZ0cot⁡ ⁡ ()β β l l ).{displaystyle Z_{mathrm {in}(ell)=-j,Z_{0}cot(beta ell).,}

Tipos prácticos

Cable coaxial

Las líneas coaxiales confinan prácticamente todas las ondas electromagnéticas al área interior del cable. Por lo tanto, las líneas coaxiales se pueden doblar y torcer (sujetas a límites) sin efectos negativos, y se pueden atar a soportes conductores sin inducir corrientes no deseadas en ellos. En aplicaciones de radiofrecuencia de hasta unos pocos gigahercios, la onda se propaga únicamente en el modo transversal eléctrico y magnético (TEM), lo que significa que los campos eléctrico y magnético son perpendiculares a la dirección de propagación (el campo eléctrico es radial y el campo magnético es circunferencial). Sin embargo, en frecuencias para las cuales la longitud de onda (en el dieléctrico) es significativamente más corta que la circunferencia del cable, se pueden propagar otros modos transversales. Estos modos se clasifican en dos grupos, modos de guía de onda eléctrica transversal (TE) y magnética transversal (TM). Cuando puede existir más de un modo, las curvas y otras irregularidades en la geometría del cable pueden hacer que la energía se transfiera de un modo a otro.

El uso más común de los cables coaxiales es para televisión y otras señales con un ancho de banda de varios megahercios. A mediados del siglo XX llevaban conexiones telefónicas de larga distancia.

Líneas planas

Las líneas de transmisión planas son líneas de transmisión con conductores o, en algunos casos, tiras dieléctricas, que son líneas planas en forma de cinta. Se utilizan para interconectar componentes en circuitos impresos y circuitos integrados que trabajan en frecuencias de microondas porque el tipo plano encaja bien con los métodos de fabricación de estos componentes. Existen varias formas de líneas de transmisión planas.

Microtira

Un tipo de línea de transmisión llamada línea de jaula, utilizado para aplicaciones de alta potencia, baja frecuencia. Funciona de forma similar a un cable coaxial grande. Este ejemplo es la línea de alimentación de la antena para un transmisor de radio de onda larga en Polonia, que opera a una frecuencia de 225 kHz y una potencia de 1200 kW.

Un circuito microstrip utiliza un conductor plano delgado que es paralelo a un plano de tierra. La microcinta se puede fabricar con una tira de cobre en un lado de una placa de circuito impreso (PCB) o sustrato de cerámica, mientras que el otro lado es un plano de tierra continuo. El ancho de la tira, el espesor de la capa aislante (PCB o cerámica) y la constante dieléctrica de la capa aislante determinan la impedancia característica. Microstrip es una estructura abierta mientras que el cable coaxial es una estructura cerrada.

Línea de franjas

Un circuito stripline utiliza una tira plana de metal que se intercala entre dos planos de tierra paralelos. El material aislante del sustrato forma un dieléctrico. El ancho de la tira, el espesor del sustrato y la permitividad relativa del sustrato determinan la impedancia característica de la tira que es una línea de transmisión.

Guía de onda coplanaria

Una guía de ondas coplanar consta de una tira central y dos conductores exteriores adyacentes, los tres son estructuras planas que se depositan sobre el mismo sustrato aislante y, por lo tanto, se ubican en el mismo plano ("coplanar"). El ancho del conductor central, la distancia entre los conductores interior y exterior y la permitividad relativa del sustrato determinan la impedancia característica de la línea de transmisión coplanar.

Líneas equilibradas

Una línea balanceada es una línea de transmisión que consta de dos conductores del mismo tipo e igual impedancia a tierra y otros circuitos. Existen muchos formatos de líneas balanceadas, entre los más comunes se encuentran el par trenzado, el cuadrete en estrella y el bifilar.

Par trenzado

Los pares trenzados se usan comúnmente para comunicaciones telefónicas terrestres. En tales cables, se agrupan muchos pares en un solo cable, desde dos hasta varios miles. El formato también se usa para la distribución de redes de datos dentro de edificios, pero el cable es más caro porque los parámetros de la línea de transmisión están estrictamente controlados.

Cuatriciclo de estrellas

Star quad es un cable de cuatro conductores en el que los cuatro conductores están trenzados juntos alrededor del eje del cable. A veces se utiliza para dos circuitos, como telefonía de 4 hilos y otras aplicaciones de telecomunicaciones. En esta configuración, cada par utiliza dos conductores no adyacentes. Otras veces se utiliza para una sola línea balanceada, como aplicaciones de audio y telefonía de 2 hilos. En esta configuración, dos conductores no adyacentes terminan juntos en ambos extremos del cable y los otros dos conductores también terminan juntos.

Cuando se utiliza para dos circuitos, la diafonía se reduce en relación con los cables con dos pares trenzados separados.

Cuando se usa para una sola línea balanceada, la interferencia magnética captada por el cable llega como una señal de modo común prácticamente perfecta, que se elimina fácilmente mediante transformadores de acoplamiento.

Los beneficios combinados de la torsión, la señalización balanceada y el patrón de cuadrupolo brindan una excelente inmunidad al ruido, especialmente ventajoso para aplicaciones de bajo nivel de señal, como cables de micrófono, incluso cuando se instalan muy cerca de un cable de alimentación. La desventaja es que el cuádruple en estrella, al combinar dos conductores, normalmente tiene el doble de capacitancia que un cable de audio blindado y trenzado similar de dos conductores. La alta capacitancia provoca una distorsión cada vez mayor y una mayor pérdida de frecuencias altas a medida que aumenta la distancia.

Doble derivación

Los conductores gemelos consisten en un par de conductores separados por un aislante continuo. Manteniendo los conductores separados por una distancia conocida, la geometría es fija y las características de la línea son confiablemente consistentes. Tiene una pérdida más baja que el cable coaxial porque la impedancia característica del cable doble es generalmente más alta que la del cable coaxial, lo que lleva a pérdidas resistivas más bajas debido a la corriente reducida. Sin embargo, es más susceptible a la interferencia.

Líneas de lectura

Las líneas Lecher son una forma de conductor paralelo que se puede usar en UHF para crear circuitos resonantes. Son un formato práctico conveniente que llena el vacío entre los componentes agrupados (usados en HF/VHF) y las cavidades resonantes (usadas en UHF/SHF).

Línea monofilar

Anteriormente, las líneas no balanceadas se usaban mucho para la transmisión telegráfica, pero esta forma de comunicación ahora ha caído en desuso. Los cables son similares al par trenzado en el sentido de que muchos núcleos se agrupan en el mismo cable, pero solo se proporciona un conductor por circuito y no hay torsión. Todos los circuitos de la misma ruta utilizan un camino común para la corriente de retorno (retorno a tierra). Hay una versión de transmisión de energía de retorno a tierra de un solo cable en uso en muchos lugares.

Aplicaciones generales

Transferencia de señal

Las líneas de transmisión eléctrica se utilizan mucho para transmitir señales de alta frecuencia a largas o cortas distancias con una mínima pérdida de energía. Un ejemplo familiar es el cable de bajada de una antena de TV o radio al receptor.

Circuitos de línea de transmisión

También se puede construir una gran variedad de circuitos con líneas de transmisión, incluidos circuitos de adaptación de impedancia, filtros, divisores de potencia y acopladores direccionales.

Línea de transmisión escalonada

Un simple ejemplo de línea de transmisión gradual consistente en tres segmentos.

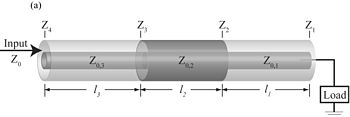
Una línea de transmisión paso se utiliza para la impedancia de amplio rango que coincide. Se puede considerar como múltiples segmentos de líneas de transmisión conectados en serie, con la impedancia característica de cada elemento individual para ser Z0,i{displaystyle Z_{mathrm {0,i} }. La impedancia de entrada puede obtenerse de la sucesiva aplicación de la relación de cadena

Zi+1=Z0,iZi+jZ0,i#⁡ ⁡ ()β β il l i)Z0,i+jZi#⁡ ⁡ ()β β il l i){displaystyle Z_{mathrm {i+1}=Z_{mathrm {0,i} {fnMicrosoft Sans Serif} {i} }+j,Z_{mathrm {0,i},tan(beta _{mathrm {i} }ell _{mathrm {i}),}{Z_{mathrm {0,i} }+j,Z_{mathrm {i},tan(beta _{mathrm {i} }ell _{mathrm {}}},}

Donde β β i{displaystyle beta _{mathrm {i}} es el número de onda del i{displaystyle mathrm {i}- segmento de la línea de transmisión l l i{displaystyle ell _{mathrm {}} es la longitud de este segmento, y Zi{displaystyle Z_{mathrm {}}} es la impedancia frontal que carga el i{displaystyle mathrm {i}- el segmento.

El círculo de transformación de impedancia a lo largo de una línea de transmisión cuya impedancia característica Z0,i{displaystyle Z_{mathrm {0,i} } es más pequeño que el cable de entrada Z0{displaystyle Z_{0}. Y como resultado, la curva de impedancia está fuera de lugar hacia el − − x{displaystyle -x. Axis. Por el contrario, si Z_{0}}" xmlns="http://www.w3.org/1998/Math/MathML">Z0,i■Z0{displaystyle Z_{mathrm {0,i}Z_{0}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1685f340564cf846e83652e782a583198afb26ad" style="vertical-align: -1.005ex; width:9.297ex; height:2.843ex;"/>, la curva de impedancia debe estar fuera de lugar hacia el +x{displaystyle +x} Axis.

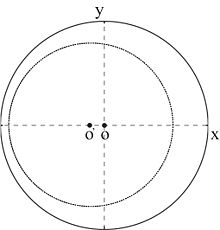
Debido a la impedancia característica de cada segmento de línea de transmisión Z0,i{displaystyle Z_{mathrm {0,i} } es a menudo diferente de la impedancia Z0{displaystyle Z_{0} del cuarto cable de entrada (sólo se muestra como una flecha marcada Z0{displaystyle Z_{0} en el lado izquierdo del diagrama anterior), el círculo de transformación de impedancia está fuera de centrado a lo largo de x{displaystyle x} eje del Gráfico Smith cuya representación de impedancia se normaliza generalmente contra Z0{displaystyle Z_{0}.

Filtros de punta

Si una línea de transmisión en cortocircuito o en circuito abierto se conecta en paralelo con una línea utilizada para transferir señales del punto A al punto B, entonces funcionará como un filtro. El método para hacer stubs es similar al método para usar líneas de Lecher para la medición de frecuencia bruta, pero 'funciona al revés'. Un método recomendado en el manual de radiocomunicaciones de RSGB es tomar una longitud de línea de transmisión en circuito abierto conectada en paralelo con el alimentador que envía señales desde una antena. Al cortar el extremo libre de la línea de transmisión, se puede encontrar un mínimo en la intensidad de la señal observada en un receptor. En esta etapa, el filtro stub rechazará esta frecuencia y los armónicos impares, pero si el extremo libre del stub está cortocircuitado, el stub se convertirá en un filtro que rechazará los armónicos pares.

Los filtros de banda ancha se pueden lograr usando varios stubs. Sin embargo, esta es una técnica algo anticuada. Se pueden hacer filtros mucho más compactos con otros métodos, como resonadores de línea paralela.

Generación de pulsos

Las líneas de transmisión se utilizan como generadores de impulsos. Al cargar la línea de transmisión y luego descargarla en una carga resistiva, se puede obtener un pulso rectangular de longitud igual al doble de la longitud eléctrica de la línea, aunque con la mitad del voltaje. Una línea de transmisión de Blumlein es un dispositivo formador de pulsos relacionado que supera esta limitación. A veces se utilizan como fuentes de energía pulsada para transmisores de radar y otros dispositivos.

Sonido

La teoría de la propagación de ondas sonoras es muy similar matemáticamente a la de las ondas electromagnéticas, por lo que también se utilizan técnicas de la teoría de líneas de transmisión para construir estructuras para conducir ondas acústicas; y estas se llaman líneas de transmisión acústica.