Límite de una secuencia

La secuencia dada por los perímetros regulares n- polígonos laterales que circunscriben el círculo de la unidad tiene un límite igual al perímetro del círculo, es decir. 2π π r{displaystyle 2pi r}. La secuencia correspondiente para los polígonos inscritos tiene el mismo límite.

n{displaystyle n}	n× × pecado⁡ ⁡ ()1n){displaystyle ntimes sin left({tfrac {1}right)}
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

Como el entero positivo n{textstyle n} se vuelve más grande y más grande, el valor n× × pecado⁡ ⁡ ()1n){textstyle ntimes sin left({tfrac {1}right)} se hace arbitrariamente cercano 1{textstyle 1}. Decimos que "el límite de la secuencia n× × pecado⁡ ⁡ ()1n){textstyle ntimes sin left({tfrac {1}right)} iguales 1{textstyle 1}."

En matemáticas, la límite de una secuencia es el valor que los términos de una secuencia "tend to", y a menudo se denota utilizando el lim{displaystyle lim } símbolo (por ejemplo, limn→ → JUEGO JUEGO an{displaystyle lim _{nto infty }a_{n}). Si existe tal límite, la secuencia se llama convergente. Se dice que una secuencia que no converge divergente. El límite de una secuencia se dice que es la noción fundamental en la que el análisis matemático en última instancia descansa.

Los límites se pueden definir en cualquier espacio métrico o topológico, pero generalmente se encuentran primero en los números reales.

Historia

El filósofo griego Zenón de Elea es famoso por formular paradojas que involucran procesos limitantes.

Leucipo, Demócrito, Antífona, Eudoxo y Arquímedes desarrollaron el método de agotamiento, que utiliza una secuencia infinita de aproximaciones para determinar un área o un volumen. Arquímedes logró sumar lo que ahora se llama una serie geométrica.

Grégoire de Saint-Vincent dio la primera definición de límite (terminal) de una serie geométrica en su obra Opus Geometricum (1647): "The terminus de una progresión es el final de la serie, al que ninguna progresión puede llegar, ni siquiera si se continúa en el infinito, pero al que puede acercarse más que un segmento dado."

Newton trató de series en sus obras Análisis con serie infinita (escrito en 1669, distribuido en manuscrito, publicado en 1711), Método de fluxiones y series infinitas (escrito en 1671, publicado en traducción al inglés en 1736, original latino publicado mucho más tarde) y Tractatus de Quadratura Curvarum (escrito en 1693, publicado en 1704 como Apéndice de su Optiks). En este último trabajo, Newton considera la expansión binomio ()x+o)n{textstyle (x+o)}{n}, que luego linealiza toman el límite como o{textstyle o} tiende a 0{textstyle 0}.

En el siglo XVIII, matemáticos como Euler lograron sumar algunas series divergentes deteniéndose en el momento adecuado; no les importaba mucho si existía un límite, siempre que pudiera calcularse. A finales de siglo, Lagrange en su Théorie des fonctions analytiques (1797) opinó que la falta de rigor impedía un mayor desarrollo del cálculo. Gauss en su estudio de series hipergeométricas (1813) por primera vez investigó rigurosamente las condiciones bajo las cuales una serie convergía a un límite.

La definición moderna de un límite (para cualquier ε ε {textstyle varepsilon } existe un índice N{textstyle N} así que...) fue dado por Bernard Bolzano (Der binomische Lehrsatz, Praga 1816, que fue poco notado en ese momento), y por Karl Weierstrass en los años 1870.

Números reales

La trama de una secuencia convergente {a_n} se muestra en azul. Aquí, se puede ver que la secuencia está convergendo al límite 0 como n aumenta.

En los números reales, un número L{displaystyle L. es límite de la secuencia ()xn){displaystyle (x_{n}}, si los números en la secuencia se acercan más y más L{displaystyle L., y no a ningún otro número.

Ejemplos

• Si xn=c{displaystyle x_{n}=c} para constante c{textstyle c}, entonces xn→ → c{displaystyle x_{n}to c}.
• Si xn=1n{displaystyle x_{n}={frac {1}{n}}, entonces xn→ → 0{displaystyle x_{n}to 0}.
• Si xn=1n{displaystyle x_{n}={frac {1}{n}} cuando n{displaystyle n} es incluso, y xn=1n2{displaystyle x_{n}={frac {1}{n^{2}}} cuando n{displaystyle n} es extraño, entonces xn→ → 0{displaystyle x_{n}to 0}. (El hecho de que x_{n}}" xmlns="http://www.w3.org/1998/Math/MathML">xn+1■xn{displaystyle x_{n+1} títulox_{n}x_{n}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/88ea8ac409f813afbeff842769723994ffd3cb36" style="vertical-align: -0.671ex; width:10.295ex; height:2.176ex;"/> siempre n{displaystyle n} es extraño es irrelevante.)
• Dado cualquier número real, uno puede fácilmente construir una secuencia que converge a ese número tomando aproximaciones decimales. Por ejemplo, la secuencia 0.3,0.33,0.333,0.3333,...... {textstyle 0.3,0.33,0.333,0.3333,dots } convergencias a 13{textstyle {frac {1}{3}}. Note que la representación decimal 0.3333...... {textstyle 0.3333dots} es límite de la secuencia anterior, definida por
  0.3333...:=limn→ → JUEGO JUEGO .. k=1n310k{displaystyle 0.3333...:=lim _{nto infty }sum _{k=1}^{n}{n}{frac {3}{10^ {k}}}

  
• Encontrar el límite de una secuencia no siempre es obvio. Dos ejemplos limn→ → JUEGO JUEGO ()1+1n)n{displaystyle lim _{ntoinfty }left(1+{tfrac {1}{n}right)^{n}} (el límite es el número e) y la media aritmética-geométrica. El teorema de presión suele ser útil en el establecimiento de tales límites.

Definición

Nosotros llamamos x{displaystyle x} el límite de la secuencia ()xn){displaystyle (x_{n}}, que está escrito

xn→ → x{displaystyle x_{n}to x}, o

limn→ → JUEGO JUEGO xn=x{displaystyle lim _{nto infty }x_{n}=x},

si se cumple la siguiente condición:

Para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>, existe un número natural N{displaystyle N} tal que, por cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos <math alttext="{displaystyle |x_{n}-x|Silencioxn− − xSilencio.ε ε {displaystyle Silencio.<img alt="{displaystyle |x_{n}-x|.

En otras palabras, por cada medida de cercanía ε ε {displaystyle varepsilon }, los términos de la secuencia son eventualmente tan cerca del límite. La secuencia ()xn){displaystyle (x_{n}} se dice que converger o tiende a el límite x{displaystyle x}.

Simbólicamente, esto es:

0left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n}-x|О О ε ε ■0()∃ ∃ N▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ Silencioxn− − xSilencio.ε ε ))){displaystyle forall varepsilon √0left(exists) Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies tenciónx_{n}-x perpetuación escritavarepsilon right)right)right)}0left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n}-x|.

Si una secuencia ()xn){displaystyle (x_{n}} converge a algún límite x{displaystyle x}, entonces es convergente y x{displaystyle x} es el único límite; de lo contrario ()xn){displaystyle (x_{n}} es divergente. Una secuencia que tiene cero como su límite a veces se llama secuencia null.

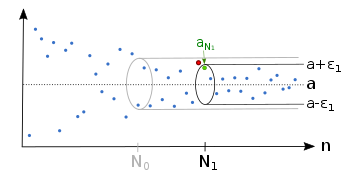
Ilustración

• 

  Ejemplo de una secuencia que converge al límite a{displaystyle a}.

• 

  Independientemente de cuál 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> tenemos, hay un índice N0{displaystyle N_{0}, por lo que la secuencia se encuentra después completamente en el tubo epsilon ()a− − ε ε ,a+ε ε ){displaystyle (a-varepsilona+varepsilon)}.

• 

  También hay para un menor 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε 1■0{displaystyle varepsilon ¿Qué?0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7735fb81938ddaa47ca75578f95010e4e3c4ec28" style="vertical-align: -0.671ex; width:6.399ex; height:2.509ex;"/> un índice N1{displaystyle N_{1}, por lo que la secuencia es después dentro del tubo epsilon ()a− − ε ε 1,a+ε ε 1){displaystyle (a-varepsilon _{1},a+varepsilon _{1})}.

• 

  Para cada uno 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> hay sólo finitamente muchos miembros de secuencia fuera del tubo de epsilon.

Propiedades

Algunas otras propiedades importantes de los límites de las sucesiones reales incluyen las siguientes:

• Cuando existe, el límite de una secuencia es único.
• Los límites de las secuencias se comportan bien con respecto a las operaciones aritméticas habituales. Si limn→ → JUEGO JUEGO an{displaystyle lim _{nto infty }a_{n} y limn→ → JUEGO JUEGO bn{displaystyle lim _{nto infty }b_{n} existe, entonces

limn→ → JUEGO JUEGO ()an± ± bn)=limn→ → JUEGO JUEGO an± ± limn→ → JUEGO JUEGO bn{displaystyle lim _{nto infty }(a_{n}pm b_{n})=lim _{nto infty }a_{n}pm lim _{nto infty }b_{n}

limn→ → JUEGO JUEGO can=c⋅ ⋅ limn→ → JUEGO JUEGO an{displaystyle lim _{nto infty }ca_{n}=ccdot lim _{nto infty }a_{n}

limn→ → JUEGO JUEGO ()an⋅ ⋅ bn)=()limn→ → JUEGO JUEGO an)⋅ ⋅ ()limn→ → JUEGO JUEGO bn){displaystyle lim _{nto infty }(a_{n}cdot b_{n})=left(lim _{nto infty }a_{n}right)cdot left(lim _{nto infty }b_{n}right)}

limn→ → JUEGO JUEGO ()anbn)=limn→ → JUEGO JUEGO anlimn→ → JUEGO JUEGO bn{displaystyle lim _{nto infty }left({frac {fn} {fn}}derecha)={frac {lim limits _{nto infty {}a_{n}{lim limits _{nto infty - Sí. proporcionadas limn→ → JUEGO JUEGO bnل ل 0{displaystyle lim _{nto infty }b_{n}neq 0}

limn→ → JUEGO JUEGO anp=()limn→ → JUEGO JUEGO an)p{displaystyle lim _{nto infty }a_{n} {p}=left(lim _{nto infty - Sí.

• Para cualquier función continua f{textstyle f}, si limn→ → JUEGO JUEGO xn{displaystyle lim _{nto infty }x_{n} existe, entonces limn→ → JUEGO JUEGO f()xn){displaystyle lim _{nto infty }fleft(x_{n}right)} existe también. De hecho, cualquier función de valor real f{textstyle f} es continuo si y sólo si preserva los límites de las secuencias (aunque esto no es necesariamente cierto al utilizar nociones más generales de continuidad).

• Si an≤ ≤ bn{displaystyle a_{n}leq B_{n} para todos n{displaystyle n} más grande que algunos N{displaystyle N}, entonces limn→ → JUEGO JUEGO an≤ ≤ limn→ → JUEGO JUEGO bn{displaystyle lim _{nto infty }a_{n}leq lim _{nto infty }b_{n}.
• (Squeeze theorem) Si an≤ ≤ cn≤ ≤ bn{displaystyle a_{n}leq C_{n}leq B_{n} para todos n{displaystyle n} más grande que algunos N{displaystyle N}, y limn→ → JUEGO JUEGO an=limn→ → JUEGO JUEGO bn=L{displaystyle lim _{nto infty }a_{n}=lim _{nto infty }b_{n}=L}, entonces limn→ → JUEGO JUEGO cn=L{displaystyle lim _{nto infty }c_{n}=L}.
• (Monotone convergence theorem) Si an{displaystyle a_{n} está atado y monotónico para todos n{displaystyle n} más grande que algunos N{displaystyle N}Entonces es convergente.
• Una secuencia es convergente si y sólo si cada subsequencia es convergente.
• Si cada subsequencia de una secuencia tiene su propia subsequencia que converge al mismo punto, entonces la secuencia original converge a ese punto.

Estas propiedades se utilizan ampliamente para demostrar límites, sin la necesidad de utilizar directamente la engorrosa definición formal. Por ejemplo, una vez que se demuestre que 1/n→ → 0{displaystyle 1/nto 0}, se hace fácil mostrar - usando las propiedades arriba - que ab+cn→ → ab{displaystyle {frac {a}{b+{frac {n}}to} {fn} {to} {f}} {fn}}} {f}}}} {fn}}}}} {fn}}} {f}}} {f}}}} {f}}}}}}}}}}}}}} { {fnK} {fnMicroc} {fnK}}} {fnK}}}} {fnK}}}} {fn}}}}}} {fnK}}} {fnK}}}}}}}} {fnK}}}}}} (suponiendo que bل ل 0{displaystyle bneq 0}).

Límites infinitos

Una secuencia ()xn){displaystyle (x_{n}} se dice que tienden a infinito, escrito

xn→ → JUEGO JUEGO {displaystyle x_{n}to infty }, o

limn→ → JUEGO JUEGO xn=JUEGO JUEGO {displaystyle lim _{nto infty }x_{n}=infty,

si se cumple lo siguiente:

Por cada número real K{displaystyle K}, hay un número natural N{displaystyle N} tal que por cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos K}" xmlns="http://www.w3.org/1998/Math/MathML">xn■K{displaystyle x_{n} {}}}K" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0a816f6e76fff7c5327caa3d024d35780f07f8b8" style="vertical-align: -0.671ex; width:7.713ex; height:2.509ex;"/>; es decir, los términos de secuencia son eventualmente más grandes que cualquier K{displaystyle K}.

Simbólicamente, esto es:

Kright)right)right)}" xmlns="http://www.w3.org/1998/Math/MathML">О О K▪ ▪ R()∃ ∃ N▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ xn■K))){displaystyle forall Kin mathbb {R} left(existidos) Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies x_{n} {Kright)right)}}Kright)right)right)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6a712f8f0d97cc793434ebe1fa5fc8f7452a15a5" style="vertical-align: -0.838ex; width:50.203ex; height:2.843ex;"/>.

Del mismo modo, decimos que una secuencia tiende a menos infinito, escrita

xn→ → − − JUEGO JUEGO {displaystyle x_{n}to -infty }, o

limn→ → JUEGO JUEGO xn=− − JUEGO JUEGO {displaystyle lim _{nto infty }x_{n}=-infty,

si se cumple lo siguiente:

Por cada número real K{displaystyle K}, hay un número natural N{displaystyle N} tal que por cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos <math alttext="{displaystyle x_{n}xn.K{displaystyle x_{n}<img alt="x_{n}; es decir, los términos de secuencia son eventualmente más pequeños que cualquier K{displaystyle K}.

Simbólicamente, esto es:

<math alttext="{displaystyle forall Kin mathbb {R} left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies x_{n}О О K▪ ▪ R()∃ ∃ N▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ xn.K))){displaystyle forall Kin mathbb {R} left(existidos) Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies) ################<img alt="{displaystyle forall Kin mathbb {R} left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies x_{n}.

Si una secuencia tiende a infinito o menos infinito, entonces es divergente. Sin embargo, una secuencia divergente no necesita tender a más o menos infinito, y la secuencia xn=()− − 1)n{displaystyle x_{n}=(-1)}{n} proporciona uno de esos ejemplos.

Espacios métricos

Definición

Un punto x{displaystyle x} del espacio métrico ()X,d){displaystyle (X,d)} es límite de la secuencia ()xn){displaystyle (x_{n}} si:

Para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>, hay un número natural N{displaystyle N} tal que, por cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos <math alttext="{displaystyle d(x_{n},x)d()xn,x).ε ε {displaystyle d(x_{n},x) segÃonvarepsilon<img alt="{displaystyle d(x_{n},x).

Simbólicamente, esto es:

0left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies d(x_{n},x)О О ε ε ■0()∃ ∃ N▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ d()xn,x).ε ε ))){displaystyle forall varepsilon √0left(exists) Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies d(x_{n},x) madevarepsilon right)right)right)}0left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies d(x_{n},x).

Esto coincide con la definición dada para números reales cuando X=R{displaystyle X=Mathbb {R} y d()x,Sí.)=Silenciox− − Sí.Silencio{displaystyle d(x,y)=vivx-y habit}.

Propiedades

• Cuando existe, el límite de una secuencia es único, ya que puntos distintos están separados por alguna distancia positiva, por lo que ε ε {displaystyle varepsilon } menos de la mitad de esta distancia, los términos de secuencia no pueden estar a una distancia ε ε {displaystyle varepsilon } de ambos puntos.

• Para cualquier función continua f, si limn→ → JUEGO JUEGO xn{displaystyle lim _{nto infty }x_{n} existe, entonces limn→ → JUEGO JUEGO f()xn)=f()limn→ → JUEGO JUEGO xn){displaystyle lim _{nto infty }f(x_{n})=fleft(lim _{nto infty }x_{n}right)}. De hecho, una función f es continuo si y sólo si preserva los límites de las secuencias.

Secuencias de Cauchy

La trama de una secuencia Cauchy (x_n), mostrado en azul, como xn{displaystyle x_{n} versus n. Visualmente, vemos que la secuencia parece estar convergendo a un punto límite a medida que los términos de la secuencia se vuelven más unidos como n aumenta. En los números reales cada secuencia Cauchy converge a algún límite.

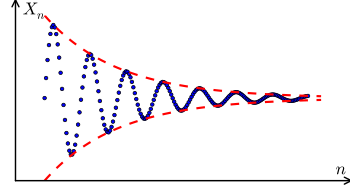
Una sucesión de Cauchy es una sucesión cuyos términos finalmente se acercan arbitrariamente, después de que se hayan descartado suficientes términos iniciales. La noción de sucesión de Cauchy es importante en el estudio de sucesiones en espacios métricos y, en particular, en el análisis real. Un resultado particularmente importante en el análisis real es el criterio de Cauchy para la convergencia de sucesiones: una sucesión de números reales es convergente si y sólo si es una sucesión de Cauchy. Esto sigue siendo cierto en otros espacios métricos completos.

Espacios topológicos

Definición

Un punto x▪ ▪ X{displaystyle xin X} del espacio topológico ()X,τ τ ){displaystyle (X,tau)} es un límite o punto límite de la secuencia ()xn)n▪ ▪ N{displaystyle left(x_{n}right)_{nin mathbb {N} si:

Por cada barrio U{displaystyle U} de x{displaystyle x}, hay algunos N▪ ▪ N{displaystyle Nin mathbb {N} por cada uno n≥ ≥ N{displaystyle ngeq N}, tenemos xn▪ ▪ U{displaystyle x_{n}in U}.

Esto coincide con la definición dada para los espacios métricos, si ()X,d){displaystyle (X,d)} es un espacio métrico y τ τ {displaystyle tau } es la topología generada por d{displaystyle d}.

Un límite de una secuencia de puntos ()xn)n▪ ▪ N{displaystyle left(x_{n}right)_{nin mathbb {N} en un espacio topológico T{displaystyle T} es un caso especial de un límite de una función: el dominio es N{displaystyle mathbb {N} en el espacio N∪ ∪ {}+JUEGO JUEGO }{displaystyle mathbb {N} cup lbrace +infty rbrace }, con la topología inducida del sistema de número real afinalmente extendido, el rango es T{displaystyle T}, y el argumento de la función n{displaystyle n} tiende a +JUEGO JUEGO {displaystyle +infty }, que en este espacio es un punto límite N{displaystyle mathbb {N}.

Propiedades

En un espacio Hausdorff, los límites de las secuencias son únicos cuando existen. Tenga en cuenta que esta necesidad no es el caso en espacios no Hausdorff; en particular, si dos puntos x{displaystyle x} y Sí.{displaystyle y} son topológicamente indistinguibles, entonces cualquier secuencia que converge x{displaystyle x} debe converger Sí.{displaystyle y} y viceversa.

Números hiperreales

La definición del límite usando los números hiperreal formaliza la intuición que para un valor "muy grande" del índice, el término correspondiente es "muy cercano" al límite. Más precisamente, una secuencia real ()xn){displaystyle (x_{n}} tiende a L si por cada infinita hipernatural H{textstyle H}, el término xH{displaystyle x_{H} está infinitamente cerca L{textstyle L} (es decir, la diferencia xH− − L{displaystyle x_{H}-L} es infinitesimal). Equivalentemente, L es la parte estándar de xH{displaystyle x_{H}:

L=st()xH){displaystyle L={rm}(x_{H}}.

Por lo tanto, el límite se puede definir mediante la fórmula

limn→ → JUEGO JUEGO xn=st()xH){displaystyle lim _{nto infty }x_{n}={rm {st}(x_{H}}.

donde el límite existe si y sólo si el lado derecho es independiente de la elección de un infinito H{textstyle H}.

Secuencia de más de un índice

A veces uno también puede considerar una secuencia con más de un índice, por ejemplo, una doble secuencia ()xn,m){displaystyle (x_{n,m})}. Esta secuencia tiene un límite L{displaystyle L. si se acerca y se acerca L{displaystyle L. cuando ambos n y m se vuelve muy grande.

Ejemplo

• Si xn,m=c{displaystyle x_{n,m}=c} para constante c{textstyle c}, entonces xn,m→ → c{displaystyle x_{n,m}to c}.
• Si xn,m=1n+m{displaystyle x_{n,m}={frac {1}{n+m}}, entonces xn,m→ → 0{displaystyle x_{n,m}to 0}.
• Si xn,m=nn+m{displaystyle x_{n,m}={frac {n} {n+m}}, entonces el límite no existe. Dependiendo de la relativa "velocidad creciente" de n{textstyle n} y m{textstyle m}, esta secuencia puede acercarse a cualquier valor entre 0{textstyle 0} y 1{textstyle 1}.

Definición

Nosotros llamamos x{displaystyle x} el doble límite de la secuencia ()xn,m){displaystyle (x_{n,m})}, escrito

xn,m→ → x{displaystyle x_{n,m}to x}, o

limn→ → JUEGO JUEGO m→ → JUEGO JUEGO xn,m=x{displaystyle lim _{begin{smallmatrix}nto infty \mto infty end{smallmatrix}x_{n,m}=x},

si se cumple la siguiente condición:

Para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>, existe un número natural N{displaystyle N} tal que, por cada par de números naturales n,m≥ ≥ N{displaystyle n,mgeq N}, tenemos <math alttext="{displaystyle |x_{n,m}-x|Silencioxn,m− − xSilencio.ε ε {displaystyle Silenciox_{n,m}-x ocultadovarepsilon }<img alt="{displaystyle |x_{n,m}-x|.

En otras palabras, por cada medida de cercanía ε ε {displaystyle varepsilon }, los términos de la secuencia son eventualmente tan cerca del límite. La secuencia ()xn,m){displaystyle (x_{n,m})} se dice que converger o tiende a el límite x{displaystyle x}.

Simbólicamente, esto es:

0left(exists Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies |x_{n,m}-x|О О ε ε ■0()∃ ∃ N▪ ▪ N()О О n,m▪ ▪ N()n,m≥ ≥ N⟹ ⟹ Silencioxn,m− − xSilencio.ε ε ))){displaystyle forall varepsilon √0left(exists) Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies vulx_{n,m}-x perpetuación escritavarepsilon right)right)}0left(exists Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies |x_{n,m}-x|.

Tenga en cuenta que el límite doble es diferente de tomar el límite en n primero y luego en m. Este último se conoce como límite iterado. Dado que tanto el límite doble como el límite iterado existen, tienen el mismo valor. Sin embargo, es posible que uno de ellos exista pero el otro no.

Límites infinitos

Una secuencia ()xn,m){displaystyle (x_{n,m})} se dice que tienden a infinito, escrito

xn,m→ → JUEGO JUEGO {displaystyle x_{n,m}to infty }, o

limn→ → JUEGO JUEGO m→ → JUEGO JUEGO xn,m=JUEGO JUEGO {displaystyle lim _{begin{smallmatrix}nto infty \mto infty end{smallmatrix}x_{n,m}=infty },

si se cumple lo siguiente:

Por cada número real K{displaystyle K}, hay un número natural N{displaystyle N} tal que por cada par de números naturales n,m≥ ≥ N{displaystyle n,mgeq N}, tenemos K}" xmlns="http://www.w3.org/1998/Math/MathML">xn,m■K{displaystyle #K}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3020cb808bc6a6f4881d2ef437a4dbb6e8550fe8" style="vertical-align: -1.005ex; width:9.613ex; height:2.843ex;"/>; es decir, los términos de secuencia son eventualmente más grandes que cualquier K{displaystyle K}.

Simbólicamente, esto es:

Kright)right)right)}" xmlns="http://www.w3.org/1998/Math/MathML">О О K▪ ▪ R()∃ ∃ N▪ ▪ N()О О n,m▪ ▪ N()n,m≥ ≥ N⟹ ⟹ xn,m■K))){displaystyle forall Kin mathbb {R} left(existidos) Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies x_{n,m} {Kright)right)}}Kright)right)right)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b74cc083dc3f2201808116cabaa85ebb47172b4b" style="vertical-align: -1.005ex; width:58.252ex; height:3.009ex;"/>.

Del mismo modo, una secuencia ()xn,m){displaystyle (x_{n,m})} tiende a menos infinito, escrito

xn,m→ → − − JUEGO JUEGO {displaystyle x_{n,m}to -infty }, o

limn→ → JUEGO JUEGO m→ → JUEGO JUEGO xn,m=− − JUEGO JUEGO {displaystyle lim _{begin{smallmatrix}nto infty \mto infty end{smallmatrix}}x_{n,m}=-infty },

si se cumple lo siguiente:

Por cada número real K{displaystyle K}, hay un número natural N{displaystyle N} tal que por cada par de números naturales n,m≥ ≥ N{displaystyle n,mgeq N}, tenemos <math alttext="{displaystyle x_{n,m}xn,m.K{displaystyle x_{n,m}traducido}<img alt="{displaystyle x_{n,m}; es decir, los términos de secuencia son eventualmente más pequeños que cualquier K{displaystyle K}.

Simbólicamente, esto es:

<math alttext="{displaystyle forall Kin mathbb {R} left(exists Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies x_{n,m}О О K▪ ▪ R()∃ ∃ N▪ ▪ N()О О n,m▪ ▪ N()n,m≥ ≥ N⟹ ⟹ xn,m.K))){displaystyle forall Kin mathbb {R} left(existidos) Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies x_{n,m} madeKright)right)}<img alt="{displaystyle forall Kin mathbb {R} left(exists Nin mathbb {N} left(forall n,min mathbb {N} left(n,mgeq Nimplies x_{n,m}.

Si una secuencia tiende a infinito o menos infinito, entonces es divergente. Sin embargo, una secuencia divergente no necesita tender a más o menos infinito, y la secuencia xn,m=()− − 1)n+m{displaystyle x_{n,m}=(-1)^{n+m} proporciona uno de esos ejemplos.

Límites puntuales y límites uniformes

Para una doble secuencia ()xn,m){displaystyle (x_{n,m})}, podemos tomar límite en uno de los índices, digamos, n→ → JUEGO JUEGO {displaystyle nto infty }, para obtener una sola secuencia ()Sí.m){displaystyle (y_{m}}. De hecho, hay dos significados posibles al tomar este límite. El primero se llama límite del punto de vista, denotado

xn,m→ → Sí.mpunto a punto{displaystyle x_{n,m}to Y..., o

limn→ → JUEGO JUEGO xn,m=Sí.mpunto a punto{displaystyle lim _{nto infty }x_{n,m}=y_{m}quad {text{pointwise}},

que significa:

Para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> y cada número natural fijo m{displaystyle m}, existe un número natural 0}" xmlns="http://www.w3.org/1998/Math/MathML">N()ε ε ,m)■0{displaystyle N(varepsilonm)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4dce65bdad83a08d9fadc190053e917f35ec47fc" style="vertical-align: -0.838ex; width:12.292ex; height:2.843ex;"/> tal que, por cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos <math alttext="{displaystyle |x_{n,m}-y_{m}|Silencioxn,m− − Sí.mSilencio.ε ε {displaystyle Silencio.<img alt="{displaystyle |x_{n,m}-y_{m}|.

Simbólicamente, esto es:

0left(forall min mathbb {N} left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n,m}-y_{m}|О О ε ε ■0()О О m▪ ▪ N()∃ ∃ N▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ Silencioxn,m− − Sí.mSilencio.ε ε )))){displaystyle forall varepsilon √0left(forall min mathbb {N} left(existidos) Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies latitudx_{n,m}-y_{m} perpetuación escritavarepsilon right)right)right)}0left(forall min mathbb {N} left(exists Nin mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n,m}-y_{m}|.

Cuando existe tal límite, decimos la secuencia ()xn,m){displaystyle (x_{n,m})} converge punto a punto ()Sí.m){displaystyle (y_{m}}.

El segundo se llama límite uniforme, denotado

xn,m→ → Sí.muniformemente{displaystyle x_{n,m}to Y...,

limn→ → JUEGO JUEGO xn,m=Sí.muniformemente{displaystyle lim _{nto infty }x_{n,m}=y_{m}quad {text{uniformly}},

xn,m⇉ ⇉ Sí.m{displaystyle x_{n,m}rightarrows Y..., o

uniflimn→ → JUEGO JUEGO xn,m=Sí.m{displaystyle {underset {ntoinfty}{mathrm {unif} lim };x_{n,m}=y_{m},

que significa:

Para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>, existe un número natural 0}" xmlns="http://www.w3.org/1998/Math/MathML">N()ε ε )■0{displaystyle N(varepsilon)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c1b107d97e8f6a926bbf733e238f449bc0a96e6d" style="vertical-align: -0.838ex; width:9.217ex; height:2.843ex;"/> tal que, por cada número natural m{displaystyle m} y para cada número natural n≥ ≥ N{displaystyle ngeq N}, tenemos <math alttext="{displaystyle |x_{n,m}-y_{m}|Silencioxn,m− − Sí.mSilencio.ε ε {displaystyle Silencio.<img alt="{displaystyle |x_{n,m}-y_{m}|.

Simbólicamente, esto es:

0left(exists Nin mathbb {N} left(forall min mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n,m}-y_{m}|О О ε ε ■0()∃ ∃ N▪ ▪ N()О О m▪ ▪ N()О О n▪ ▪ N()n≥ ≥ N⟹ ⟹ Silencioxn,m− − Sí.mSilencio.ε ε )))){displaystyle forall varepsilon √0left(exists) Nin mathbb {N} left(forall min mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies tenciónx_{n,m}-y_{m} arrestadovarepsilon right)right)right)}0left(exists Nin mathbb {N} left(forall min mathbb {N} left(forall nin mathbb {N} left(ngeq Nimplies |x_{n,m}-y_{m}|.

En esta definición, la elección de N{displaystyle N} es independiente de m{displaystyle m}. En otras palabras, la elección de N{displaystyle N} es aplicable uniformemente a todos los números naturales m{displaystyle m}. Por lo tanto, se puede ver fácilmente que la convergencia uniforme es una propiedad más fuerte que la convergencia puntual: la existencia de límite uniforme implica la existencia e igualdad de límite puntero:

Si xn,m→ → Sí.m{displaystyle x_{n,m}to Y... uniformemente, entonces xn,m→ → Sí.m{displaystyle x_{n,m}to Y... En sentido de punto.

Cuando existe tal límite, decimos la secuencia ()xn,m){displaystyle (x_{n,m})} converge uniformemente a ()Sí.m){displaystyle (y_{m}}.

Límite iterado

Para una doble secuencia ()xn,m){displaystyle (x_{n,m})}, podemos tomar límite en uno de los índices, digamos, n→ → JUEGO JUEGO {displaystyle nto infty }, para obtener una sola secuencia ()Sí.m){displaystyle (y_{m}}, y luego tomar límite en el otro índice, m→ → JUEGO JUEGO {displaystyle mto infty}, para conseguir un número Sí.{displaystyle y}. Simbólicamente,

limm→ → JUEGO JUEGO limn→ → JUEGO JUEGO xn,m=limm→ → JUEGO JUEGO Sí.m=Sí.{displaystyle lim _{mto infty }lim _{nto infty }x_{n,m}=lim _{mto infty Sí..

Este límite se conoce como límite iterado de la doble secuencia. Tenga en cuenta que el orden de tomar los límites puede afectar el resultado, es decir,

limm→ → JUEGO JUEGO limn→ → JUEGO JUEGO xn,mل ل limm→ → JUEGO JUEGO limn→ → JUEGO JUEGO xn,m{displaystyle lim _{mto infty }lim _{nto infty }x_{n,m}neq lim _{mto infty }lim _{nto infty }x_{n,m} en general.

Una condición suficiente de igualdad es dada por el teorema Moore-Osgood, que requiere el límite limn→ → JUEGO JUEGO xn,m=Sí.m{displaystyle lim _{nto infty }x_{n,m}=y_{m} para ser uniforme m{textstyle m}.