Límite de grano

En ciencia de materiales, un límite de grano es la interfaz entre dos granos, o cristalitos, en un material policristalino. Los límites de grano son defectos bidimensionales en la estructura cristalina y tienden a disminuir la conductividad eléctrica y térmica del material. La mayoría de los límites de grano son sitios preferidos para el inicio de la corrosión y para la precipitación de nuevas fases del sólido. También son importantes para muchos de los mecanismos de fluencia. Por otro lado, los límites de grano interrumpen el movimiento de las dislocaciones a través de un material, por lo que reducir el tamaño de los cristalitos es una forma común de mejorar la resistencia mecánica, como se describe en la relación Hall-Petch.

Límites de ángulo alto y bajo

Es conveniente categorizar los límites de los granos según el grado de desorientación entre los dos granos. Los límites de grano de ángulo bajo (LAGB) o límites de subgrano son aquellos con una desorientación inferior a unos 15 grados. En general, se componen de una serie de dislocaciones y sus propiedades y estructura están en función de la desorientación. Por el contrario, las propiedades de los límites de grano de ángulo alto, cuya desorientación es superior a unos 15 grados (el ángulo de transición varía de 10 a 15 grados dependiendo del material), normalmente son independientes de la desorientación. Sin embargo, existen 'límites especiales' en orientaciones particulares cuyas energías interfaciales son marcadamente más bajas que las de los límites generales de grano de alto ángulo.

El límite más simple es el de un límite de inclinación donde el eje de rotación es paralelo al plano límite. Se puede concebir que este límite se forma a partir de un único cristalito o grano contiguo que se dobla gradualmente por alguna fuerza externa. La energía asociada con la flexión elástica de la red se puede reducir insertando una dislocación, que es esencialmente un semiplano de átomos que actúa como una cuña, que crea una desorientación permanente entre los dos lados. A medida que el grano se dobla más, se deben introducir más y más dislocaciones para acomodar la deformación, lo que da como resultado un muro creciente de dislocaciones: un límite de ángulo bajo. Ahora se puede considerar que el grano se ha dividido en dos subgranos de cristalografía relacionada pero con orientaciones notablemente diferentes.

Una alternativa es un límite giratorio donde la desorientación ocurre alrededor de un eje que es perpendicular al plano límite. Este tipo de límite incorpora dos conjuntos de dislocaciones de tornillos. Si los vectores de Burgers de las dislocaciones son ortogonales, entonces las dislocaciones no interactúan fuertemente y forman una red cuadrada. En otros casos, las dislocaciones pueden interactuar para formar una estructura hexagonal más compleja.

Estos conceptos de límites de inclinación y torsión representan casos algo idealizados. La mayoría de los límites son de tipo mixto y contienen dislocaciones de diferentes tipos y vectores de Burgers, para crear el mejor ajuste entre los granos vecinos.

Si las dislocaciones en el límite permanecen aisladas y distintas, se puede considerar que el límite tiene un ángulo bajo. Si la deformación continúa, la densidad de las dislocaciones aumentará y, por tanto, se reducirá el espacio entre las dislocaciones vecinas. Con el tiempo, los núcleos de las dislocaciones comenzarán a superponerse y la naturaleza ordenada de la frontera comenzará a desmoronarse. En este punto se puede considerar que el límite tiene un ángulo alto y que el grano original se ha separado en dos granos completamente separados.

En comparación con los límites de grano de ángulo bajo, los límites de ángulo alto son considerablemente más desordenados, con grandes áreas de mal ajuste y una estructura comparativamente abierta. De hecho, originalmente se pensó que eran algún tipo de capa amorfa o incluso líquida entre los granos. Sin embargo, este modelo no podía explicar la fuerza observada de los límites de los granos y, después de la invención de la microscopía electrónica, la evidencia directa de la estructura de los granos obligó a descartar la hipótesis. Ahora se acepta que una frontera consta de unidades estructurales que dependen tanto de la mala orientación de los dos granos como del plano de la interfaz. Los tipos de unidad estructural que existen se pueden relacionar con el concepto de red de sitios de coincidencia, en el que se forman unidades repetidas a partir de puntos donde las dos están desorientadas. En la teoría de la red de sitios coincidentes (CSL), el grado de ajuste (Σ) entre las estructuras de los dos granos se describe mediante el recíproco de la relación entre los sitios de coincidencia y el número total de sitios. En este marco, es posible dibujar la red para los dos granos y contar el número de átomos que se comparten (sitios de coincidencia) y el número total de átomos en el límite (número total de sitios). Por ejemplo, cuando Σ=3 habrá un átomo de cada tres que se compartirá entre las dos redes. Por lo tanto, se podría esperar que una frontera con Σ alta tenga una energía mayor que una con Σ baja. Los límites de ángulo bajo, donde la distorsión se acomoda completamente mediante dislocaciones, son Σ1. Algunos otros límites de bajo Σ tienen propiedades especiales, especialmente cuando el plano límite contiene una alta densidad de sitios coincidentes. Los ejemplos incluyen límites gemelos coherentes (p. ej., Σ3) y límites de alta movilidad en materiales FCC (p. ej., Σ7). Las desviaciones de la orientación CSL ideal pueden adaptarse mediante relajación atómica local o la inclusión de dislocaciones en el límite.

Describir un límite

Un límite se puede describir mediante la orientación del límite hacia los dos granos y la rotación tridimensional requerida para que los granos coincidan. Por tanto, un límite tiene 5 grados de libertad macroscópicos. Sin embargo, es común describir un límite sólo como la relación de orientación de los granos vecinos. Generalmente, la conveniencia de ignorar la orientación del plano límite, que es muy difícil de determinar, pesa más que la información reducida. La orientación relativa de los dos granos se describe utilizando la matriz de rotación:

${\displaystyle R={\begin{bmatrix}a_{11} limita_{12} limita_{13}\a_{21} limitadaa_{22} limita_{23}\a_{31} limita_{32} {33}\end{bmatrix}}}}}}}}$

Utilizando este sistema el ángulo de rotación θ es:

${\displaystyle 2\cos \;\theta \;+1=a_{11}+a_{22}+a_{33}\,\!}$

mientras que la dirección [uvw] del eje de rotación es:

${\displaystyle [a_{32}-a_{23}),(a_{13}-a_{31}),(a_{21}-a_{12})]\,\!}$

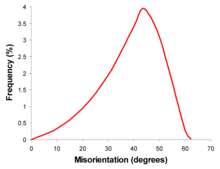
La naturaleza de la cristalografía involucrada limita la desorientación del límite. Un policristal completamente aleatorio, sin textura, tiene por tanto una distribución característica de desorientaciones de límites (ver figura). Sin embargo, estos casos son raros y la mayoría de los materiales se desviarán de este ideal en mayor o menor grado.

Energía límite

La energía de un límite de ángulo bajo depende del grado de desorientación entre los granos vecinos hasta la transición al estado de ángulo alto. En el caso de límites de inclinación simples, la energía de un límite formado por dislocaciones con el vector de Burgers b y el espaciado h se predice mediante Lea la ecuación de Shockley:

${\displaystyle \gamma _{s}=\gamma _{0}\theta (A-\ln\theta)\,\!}$

donde:

${\displaystyle \theta =b/h\,\!}$

${\displaystyle \gamma ¿Qué?$

${\displaystyle A=1+\ln(b/2\pi r_{0}\,\!$

con ${\displaystyle G.$ es el módulo de tijera, ${\displaystyle \nu }$ es la relación de Poisson, y ${\displaystyle R_{0}$ es el radio del núcleo de dislocación. Se puede ver que a medida que la energía del límite aumenta la energía por dislocación disminuye. Por lo tanto hay una fuerza motriz para producir límites menos y más mal orientados (es decir, el crecimiento del grano).

La situación en los límites de alto ángulo es más compleja. Aunque la teoría predice que la energía será un mínimo para configuraciones ideales de CSL, con desviaciones que requieren dislocaciones y otras características energéticas, las mediciones empíricas sugieren que la relación es más complicada. Algunos troughs predicho en energía se encuentran como esperado mientras que otros desaparecidos o sustancialmente reducidos. Las encuestas de los datos experimentales disponibles han indicado que relaciones simples como las bajas ${\displaystyle \Sigma$ son engañosos:

Se concluye que ningún criterio general y útil para la baja energía puede ser consagrado en un marco geométrico simple. Cualquier comprensión de las variaciones de la energía interfacial debe tener en cuenta la estructura atómica y los detalles de la unión en la interfaz.

Exceso de volumen

El volumen excesivo es otra propiedad importante en la caracterización de los límites de grano. El volumen excesivo fue propuesto por Mons. en una comunicación privada a Aaron y Bolling en 1972. Describe cuánta expansión es inducida por la presencia de un GB y se piensa que el grado y la susceptibilidad de la segregación es directamente proporcional a esto. A pesar del nombre el volumen excesivo es en realidad un cambio de longitud, esto es debido a la naturaleza 2D de GBs la longitud de interés es la expansión normal al plano GB. El volumen de exceso (${\displaystyle \delta V}$) se define de la siguiente manera,

${\displaystyle \delta V=\left({\frac {\partial V}{\partial A}\right)_{T,p,n_{i}}}}$

a temperatura constante ${\displaystyle T}$, presión ${\displaystyle p}$ y número de átomos ${\displaystyle No.$. Aunque existe una relación lineal aproximada entre la energía GB y el exceso de volumen, las orientaciones en las que se viola esta relación pueden comportarse de manera significativamente diferente afectando las propiedades mecánicas y eléctricas.

Se han desarrollado técnicas experimentales que analizan directamente el exceso de volumen y se han utilizado para explorar las propiedades del cobre y el níquel nanocristalinos. También se han desarrollado métodos teóricos que coinciden. Una observación clave es que existe una relación inversa con el módulo de volumen, lo que significa que cuanto mayor sea el módulo de volumen (la capacidad de comprimir un material), menor será el exceso de volumen; también existe una relación directa con la constante de red, esto proporciona la metodología. para encontrar materiales con un exceso de volumen deseable para una aplicación específica.

Migración fronteriza

El movimiento de los límites de grano (HAGB) tiene implicaciones para la recristalización y el crecimiento del grano, mientras que el movimiento de los límites de subgrano (LAGB) influye fuertemente en la recuperación y la nucleación de la recristalización.

Un límite se mueve debido a una presión que actúa sobre él. Generalmente se supone que la velocidad es directamente proporcional a la presión y que la constante de proporcionalidad es la movilidad del límite. La movilidad depende en gran medida de la temperatura y, a menudo, sigue una relación de tipo Arrhenius:

${\displaystyle M=M_{0}\exp \left(-{\frac {Q}\right)\,\!}$

La energía de activación aparente (Q) puede estar relacionada con los procesos atomísticos activados térmicamente que ocurren durante el movimiento de los límites. Sin embargo, existen varios mecanismos propuestos en los que la movilidad dependerá de la presión de conducción y la proporcionalidad asumida puede fracasar.

En general, se acepta que la movilidad de los límites de ángulo bajo es mucho menor que la de los límites de ángulo alto. Las siguientes observaciones parecen ser ciertas en una variedad de condiciones:

• La movilidad de los límites de bajo ángulo es proporcional a la presión que actúa sobre él.
• El proceso de control de tarifas es el de la difusión a granel
• La movilidad de límites aumenta con desorientación.

Dado que los límites de ángulo bajo están compuestos por conjuntos de dislocaciones y su movimiento puede estar relacionado con la teoría de las dislocaciones. El mecanismo más probable, dados los datos experimentales, es el de ascenso de dislocaciones, velocidad limitada por la difusión del soluto en la masa.

El movimiento de los límites de ángulo alto se produce por la transferencia de átomos entre los granos vecinos. La facilidad con la que esto puede ocurrir dependerá de la estructura del límite, que a su vez depende de la cristalografía de los granos involucrados, los átomos de impureza y la temperatura. Es posible que alguna forma de mecanismo sin difusión (similar a las transformaciones de fase sin difusión como la martensita) pueda funcionar en determinadas condiciones. Algunos defectos en la frontera, como escalones y repisas, también pueden ofrecer mecanismos alternativos para la transferencia atómica.

Dado que un límite de ángulo alto está imperfectamente empaquetado en comparación con la red normal, tiene cierta cantidad de espacio libre o volumen libre donde los átomos de soluto pueden poseer una energía más baja. Como resultado, un límite puede estar asociado con una atmósfera de soluto que retardará su movimiento. Sólo a velocidades más altas la frontera podrá liberarse de su atmósfera y reanudar su movimiento normal.

Tanto los límites de ángulo bajo como los de alto ángulo se retardan por la presencia de partículas a través del llamado efecto Zener pinning. Este efecto suele explotarse en aleaciones comerciales para minimizar o prevenir la recristalización o el crecimiento del grano durante el tratamiento térmico.

Tez

Los límites de grano son el sitio preferencial para la segregación de impurezas, que pueden formar una capa delgada con una composición diferente a la del resto y una variedad de estructuras atómicas que son distintas de las fases cristalinas contiguas. Por ejemplo, en el nitruro de silicio suele haber una fina capa de sílice, que también contiene cationes impurezas.

Ming Tang, Rowland Cannon y W. Craig Carter introdujeron las complexiones de los límites de grano en 2006.

Estas fases de límite de grano son termodinámicamente estables y pueden considerarse como fases cuasi bidimensionales, que pueden sufrir una transición, similar a las de las fases masivas. En este caso, es posible que se produzcan cambios abruptos en la estructura y la química en un valor crítico de un parámetro termodinámico como la temperatura o la presión. Esto puede afectar fuertemente las propiedades macroscópicas del material, por ejemplo la resistencia eléctrica o las tasas de fluencia. Los límites de los granos se pueden analizar utilizando la termodinámica de equilibrio, pero no se pueden considerar fases porque no satisfacen la definición de Gibbs: son no homogéneos y pueden tener un gradiente de estructura, composición o propiedades. Por este motivo se definen como complexión: un material o estado interfacial que está en equilibrio termodinámico con sus fases contiguas, con un espesor finito y estable (que suele ser de 2 a 20 Å). Un cutis necesita la fase siguiente para existir y su composición y estructura deben ser diferentes de la fase siguiente. A diferencia de las fases masivas, la tez también depende de la fase siguiente. Por ejemplo, la capa amorfa rica en sílice presente en Si₃N₃ tiene aproximadamente 10 Å de espesor, pero para límites especiales este espesor de equilibrio es cero. La tez se puede agrupar en 6 categorías, según su espesor: monocapa, bicapa, tricapa, nanocapa (con espesor de equilibrio entre 1 y 2 nm) y humectante. En los primeros casos el espesor de la capa será constante; si hay material adicional, se segregará en la unión de múltiples granos, mientras que en el último caso no hay espesor de equilibrio y esto está determinado por la cantidad de fase secundaria presente en el material. Un ejemplo de transición de la complexión del límite de grano es el paso del límite seco a la capa bicapa en Si dopado con Au, que se produce por el aumento de Au.

Efecto en la estructura electrónica

Los límites de grano pueden causar fallas mecánicas por fragilización a través de la segregación de solutos (ver Hinkley Point, una central nuclear), pero también pueden afectar perjudicialmente las propiedades electrónicas. En el caso de los óxidos metálicos se ha demostrado teóricamente que en los límites de grano de Al₂O₃ y MgO las propiedades aislantes pueden verse claramente disminuidas. Utilizando la teoría funcional de la densidad, las simulaciones por computadora de los límites de los granos han demostrado que la banda prohibida se puede reducir hasta en un 45%. En el caso de metales, los límites de grano aumentan la resistividad a medida que el tamaño de los granos en relación con el recorrido libre medio de otras dispersiones se vuelve significativo.

Concentración de defectos cerca de los límites del grano

Se sabe que la mayoría de los materiales son policristalinos y contienen límites de grano y que los límites de grano pueden actuar como sumideros y vías de transporte para defectos puntuales. Sin embargo, es difícil determinar experimental y teóricamente qué efecto tienen los defectos puntuales en un sistema. Ejemplos interesantes de las complicaciones de cómo se comportan los defectos puntuales se han manifestado en la dependencia de la temperatura del efecto Seebeck. Además, la respuesta dieléctrica y piezoeléctrica puede verse alterada por la distribución de defectos puntuales cerca de los límites de los granos. Las propiedades mecánicas también pueden verse influenciadas significativamente, ya que propiedades como el módulo de volumen y la amortiguación se ven influenciadas por cambios en la distribución de defectos puntuales dentro de un material. También se ha descubierto que el efecto Kondo dentro del grafeno se puede ajustar debido a una relación compleja entre los límites de los granos y los defectos puntuales. Cálculos teóricos recientes han revelado que los defectos puntuales pueden ser extremadamente favorables cerca de ciertos tipos de límites de grano y afectar significativamente las propiedades electrónicas con una reducción en la banda prohibida.

Relación entre teoría y experimento

Ha habido una cantidad significativa de trabajo experimental para observar tanto la estructura como medir las propiedades de los límites de los granos, pero los grados de libertad de cinco dimensiones de los límites de los granos dentro de redes policristalinas complejas aún no se han entendido completamente y, por lo tanto, actualmente no hay Método para controlar la estructura y propiedades de la mayoría de los metales y aleaciones con precisión atómica. Parte del problema está relacionado con el hecho de que gran parte del trabajo teórico para comprender los límites de los granos se basa en la construcción de (dos) granos bicristalinos que no representan la red de granos que normalmente se encuentra en un sistema real y el uso de campos de fuerza clásicos. como el método del átomo incrustado a menudo no describen correctamente la física cerca de los granos y podría ser necesaria la teoría del funcional de densidad para brindar información realista. Un modelado preciso de los límites de los granos, tanto en términos de estructura como de interacciones atómicas, podría tener el efecto de mejorar la ingeniería, lo que podría reducir el desperdicio y aumentar la eficiencia en términos de uso y rendimiento del material. Desde un punto de vista computacional gran parte de la investigación sobre límites de grano se ha centrado en sistemas bicristalinos, estos son sistemas que solo consideran dos límites de grano. Ha habido trabajos recientes que han utilizado nuevos modelos de evolución de granos que muestran que existen diferencias sustanciales en las propiedades de los materiales asociadas con la presencia de granos curvos o planos.