Leyes de Kepler del movimiento planetario

Figura 1: Ilustración de las tres leyes de Kepler con dos órbitas planetarias.

1. Las órbitas son elipses, con puntos focales F₁ y F₂ para el primer planeta y F₁ y F₃ para el segundo planeta. El Sol se coloca en el punto focal F₁.
2. Los dos sectores sombreados A₁ y A₂ tienen la misma superficie y el tiempo para el planeta 1 para cubrir segmento A₁ es igual al tiempo para cubrir el segmento A₂.
3. Los tiempos de órbita total para el planeta 1 y el planeta 2 tienen una relación ${textstyle left({frac {a_{1}{a_{2}}right) {3}{2}}$.

En astronomía, las leyes del movimiento planetario de Kepler, publicadas por Johannes Kepler entre 1609 y 1619, describen las órbitas de los planetas alrededor del Sol. Las leyes modificaron la teoría heliocéntrica de Nicolás Copérnico, sustituyendo sus órbitas circulares y epiciclos por trayectorias elípticas, y explicando cómo varían las velocidades planetarias. Las tres leyes establecen que:

1. La órbita de un planeta es un elipse con el Sol en uno de los dos focos.
2. Un segmento de línea que une un planeta y el Sol barre áreas iguales durante intervalos iguales de tiempo.
3. El cuadrado del período orbital de un planeta es proporcional al cubo de la longitud del eje semi-major de su órbita.

Las órbitas elípticas de los planetas se indicaron mediante cálculos de la órbita de Marte. A partir de esto, Kepler infirió que otros cuerpos del Sistema Solar, incluidos los más alejados del Sol, también tienen órbitas elípticas. La segunda ley ayuda a establecer que cuando un planeta está más cerca del Sol, viaja más rápido. La tercera ley expresa que cuanto más lejos está un planeta del Sol, más lenta es su velocidad orbital, y viceversa.

Isaac Newton demostró en 1687 que relaciones como las de Kepler se aplicarían en el Sistema Solar como consecuencia de sus propias leyes de movimiento y ley de gravitación universal.

Comparación con Copérnico

Las leyes de Johannes Kepler mejoraron el modelo de Copérnico. Según Copérnico:

1. La órbita planetaria es un círculo con epiciclos.
2. El Sol está aproximadamente en el centro de la órbita.
3. La velocidad del planeta en la órbita principal es constante.

A pesar de tener razón al decir que los planetas giraban alrededor del Sol, Copérnico se equivocó al definir sus órbitas. Fue Kepler quien definió correctamente la órbita de los planetas de la siguiente manera:

1. La órbita planetaria es no un círculo con epiciclos, pero un elipse.
2. El Sol es no cerca del centro pero en punto focal de la órbita elíptica.
3. Ni la velocidad lineal ni la velocidad angular del planeta en la órbita es constante, pero la velocidad de la zona (cercamente vinculado históricamente con el concepto de impulso angular) es constante.

La excentricidad de la órbita de la Tierra hace que el tiempo del equinoccio de marzo al equinoccio de septiembre, alrededor de 186 días, no sea igual al tiempo del equinoccio de septiembre al equinoccio de marzo, alrededor de 179 días. Un diámetro cortaría la órbita en partes iguales, pero el plano que pasa por el Sol paralelo al ecuador de la Tierra corta la órbita en dos partes con áreas en una proporción de 186 a 179, por lo que la excentricidad de la órbita de la Tierra es aproximadamente

${displaystyle eapprox {fnMicroc {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\\fnMicrosoft {fnMicrosoft {\\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\\\\\\\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\\fnMicrosoft {\fnMicro }{4}{frac {186-179}{186+179}approx 0.015,}$

que está cerca del valor correcto (0.016710218). La precisión de este cálculo requiere que las dos fechas elegidas estén a lo largo del eje menor de la órbita elíptica y que los puntos medios de cada mitad estén a lo largo del eje mayor. Como las dos fechas elegidas aquí son equinoccios, esto será correcto cuando el perihelio, la fecha en que la Tierra está más cerca del Sol, caiga en un solsticio. El perihelio actual, cerca del 4 de enero, está bastante cerca del solsticio del 21 o 22 de diciembre.

Nomenclatura

Se necesitaron casi dos siglos para que la formulación actual del trabajo de Kepler adquiriera su forma establecida. Eléments de la philosophie de Newton de Voltaire (Elementos de la filosofía de Newton) de 1738 fue la primera publicación en utilizar la terminología de " leyes". La Biographical Encyclopedia of Astronomers en su artículo sobre Kepler (p. 620) afirma que la terminología de las leyes científicas para estos descubrimientos estaba vigente al menos desde la época de Joseph de Lalande. Fue la exposición de Robert Small, en Relato de los descubrimientos astronómicos de Kepler (1814) la que compuso el conjunto de tres leyes, sumando la tercera. Small también afirmó, contra la historia, que se trataba de leyes empíricas, basadas en un razonamiento inductivo.

Además, el uso actual de la "segunda ley de Kepler" es algo así como un nombre inapropiado. Kepler tenía dos versiones, relacionadas en un sentido cualitativo: la "ley de distancia" y la "ley de área". La "ley de área" es lo que se convirtió en la Segunda Ley en el conjunto de tres; pero Kepler mismo no lo privilegió de esa manera.

Historia

Kepler publicó sus dos primeras leyes sobre el movimiento planetario en 1609, y las encontró analizando las observaciones astronómicas de Tycho Brahe. La tercera ley de Kepler se publicó en 1619. Kepler había creído en el modelo copernicano del Sistema Solar, que requería órbitas circulares, pero no pudo conciliar las observaciones de alta precisión de Brahe con un ajuste circular a Marte. 39; órbita: Marte tiene la excentricidad más alta de todos los planetas excepto Mercurio. Su primera ley reflejó este descubrimiento.

En 1621, Kepler observó que su tercera ley se aplica a las cuatro lunas más brillantes de Júpiter. Godefroy Wendelin también hizo esta observación en 1643. La segunda ley, en la "ley de área" forma, fue impugnada por Nicolaus Mercator en un libro de 1664, pero en 1670 sus Transacciones filosóficas estaban a su favor. A medida que avanzaba el siglo se hizo más ampliamente aceptado. La recepción en Alemania cambió notablemente entre 1688, año en que se publicaron los Principia de Newton y se los tomó como básicamente copernicanos, y 1690, cuando el trabajo de Gottfried Leibniz sobre Kepler había sido publicado. publicado.

A Newton se le atribuye haber entendido que la segunda ley no es especial de la ley del inverso del cuadrado de la gravitación, sino que es una consecuencia de la naturaleza radial de esa ley, mientras que las otras leyes sí dependen de la forma del inverso del cuadrado de la atracción. Carl Runge y Wilhelm Lenz identificaron mucho más tarde un principio de simetría en el espacio de fase del movimiento planetario (la actuación del grupo ortogonal O(4)) que explica la primera y la tercera leyes en el caso de la gravitación newtoniana, como lo hace la conservación del momento angular a través de simetría rotacional de la segunda ley.

Formulario

El modelo matemático de la cinemática de un planeta sujeto a las leyes permite una amplia gama de cálculos adicionales.

Primera ley

La órbita de cada planeta es un elipse con el Sol en uno de los dos focos.

Gráfico 2: La primera ley de Kepler colocando el Sol en el foco de una órbita elíptica

Figura 3: Sistema de coordinación heliocéntrico (r,SilencioPara elipse. También se muestra: eje semi-major a, eje semi-minor b y semi-latus recto p; centro de elipse y sus dos focos marcados por puntos grandes. Para θ = 0°, r = r_min y para θ = 180°, r = r_max.

Matemáticamente, una elipse se puede representar mediante la fórmula:

${displaystyle r={frac {p}{1+varepsilon {fnMicrosoft Sans Serif}$

Donde ${displaystyle p}$ es el recto semi-lato, ε es la excentricidad de la elipse, r es la distancia del Sol al planeta, y Silencio es el ángulo a la posición actual del planeta desde su enfoque más cercano, como se ve desde el Sol. Así que...r,Silencio) son coordenadas polares.

Para una elipse 0 < ε < 1; en el caso límite ε = 0, la órbita es un círculo con el Sol en el centro (es decir, donde hay cero excentricidad).

En θ = 0°, perihelio, la distancia es mínima

${displaystyle r_{min}={frac} {p}{1+varepsilon }$

At Silencio = 90° y a Silencio = 270° la distancia es igual a ${displaystyle p}$.

En θ = 180°, afelio, la distancia es máxima (por definición, afelio es, invariablemente, perihelio más 180°)

${displaystyle r_{max }={frac {p}{1-varepsilon }$

El semieje mayor a es la media aritmética entre r_min y r_max :

${displaystyle {begin{aligned}a ventaja={frac {r_{max }+r_{min {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {p}{1-varepsilon }end{aligned}}$

El eje semi-menor b es la media geométrica entre r_min y r_max :

${fnMicrosoftware {fnMicrosoft Sans Serif}}[3pt]b Pulse={frac={frac {fnK}} {fnK}} {fn}} {fn}}} {fn}}} {fn}}}} {fn}} {fn}}}}} {fn}}} {fn}}} {f}}}} {f}}$

El semi-latus rectum p es la media armónica entre r_min y r_max :

${displaystyle {begin{aligned}p limit=left({frac {\maxfn0}. ¿Qué? }r_{min }=b^{2},end{aligned}}$

La excentricidad ε es el coeficiente de variación entre r_min y r_max:

${displaystyle varepsilon ={frac {r_{max }-r_{min }{r_{max }+r_{min }}}$

El área de la elipse es

${displaystyle A=pi ab,$

El caso especial de un círculo es ε = 0, dando como resultado r = p = r< sub>mín = r_máx = a = b y A = πr².

Segunda ley

Una línea que une un planeta y el Sol barre áreas iguales durante intervalos iguales de tiempo.

El mismo área (azul) es barrida en un período de tiempo fijo. La flecha verde es velocidad. La flecha púrpura dirigida hacia el Sol es la aceleración. Las otras dos flechas púrpuras son componentes de aceleración paralelos y perpendiculares a la velocidad.

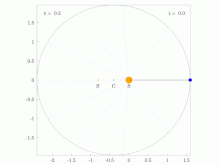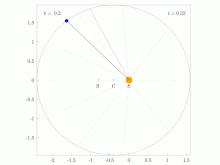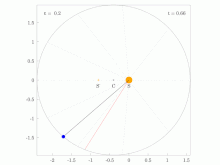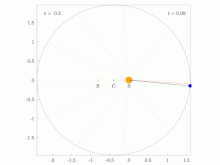
El radio orbital y la velocidad angular del planeta en la órbita elíptica variarán. Esto se muestra en la animación: el planeta viaja más rápido cuando está más cerca del Sol, luego más lento cuando está más lejos del Sol. La segunda ley de Kepler establece que el sector azul tiene área constante.

En un pequeño momento ${displaystyle dt}$ el planeta barre un pequeño triángulo con línea base ${displaystyle r}$ y altura ${displaystyle r,dtheta}$ y zona ${cdot rcdot rcdot,dtheta }$, por lo que la velocidad areal constante es

$${displaystyle {frac {}{dt}={frac} {fnK}} {fnMicroc} {fnK}}}} {fnMicroc}}} {f}}} {fn}}} {f}}}} {fn}}}} {fn}}} {f}}} {f}}}}} {fnMicroc}}}}} {f}} {f}}}}}}}}}}}}} {f}}} {f}}}}} {f} {f}}}}} {f}} {f} {f}}}} {f}}} {f}} {f}}}} {f} {f} {f} {f}}}} {f}}} {f}}}}}f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {dtheta } {dt}}}$$

El área encerrada por la órbita elíptica es ${displaystyle pi ab}$. Así que el período ${displaystyle T}$ satisfizo

${displaystyle Tcdot {frac {}{2}{2}{frac {dtheta } {dt}=pi ab$

y el movimiento medio del planeta alrededor del Sol

${displaystyle n={frac {2pi}{T}} {f}} {f}} {f}} {f}} {f}}}$

satisface

${displaystyle r^{2},dtheta =abn,dt.}$

Y así,

$${displaystyle {frac {}{dt}={frac} {abn}{2}={frac} ♪ Ab} {T}.}$$

Orbits de planetas con diferentes excentricidades. El rayo rojo gira a una velocidad angular constante y con el mismo período orbital que el planeta, ${displaystyle T=1}$. S: Sol en el foco primario, C: Centro de elipse, S': El enfoque secundario. En cada caso, el área de todos los sectores representados es idéntica.

Baja	Alto
Planeta orbitando el Sol en una órbita circular (e=0.0)	Planeta orbitando el Sol en una órbita con e=0.5
Planeta orbitando el Sol en una órbita con e=0.2	Planeta orbitando el Sol en una órbita con e=0.8

Tercera ley

La relación del cuadrado del período orbital de un objeto con el cubo del eje semi-major de su órbita es la misma para todos los objetos que orbitan la misma primaria.

Esto captura la relación entre la distancia de los planetas al Sol y sus períodos orbitales.

Kepler enunció en 1619 esta tercera ley en un laborioso intento de determinar lo que él veía como la "música de las esferas" según leyes precisas, y expresarlo en términos de notación musical. Por lo tanto, se la conoció como la ley armónica.

Usando la ley de gravitación de Newton (publicada en 1687), esta relación se puede encontrar en el caso de una órbita circular igualando la fuerza centrípeta a la fuerza gravitacional:

${displaystyle mromega ^{2}=G{frac {mM}{2}}}$

Luego, expresando la velocidad angular ω en términos del período orbital ${displaystyle {T}$ y luego reorganización, resultados en la Tercera Ley de Kepler:

${displaystyle mrleft({frac {2pi - Sí. {mM} {r^{2}}derecho T^{2}=left({frac {4pi ¿Qué? T^{2}propto r^{3}$

Una derivación más detallada se puede hacer con órbitas elípticas generales, en lugar de círculos, así como orbitando el centro de masa, en lugar de sólo la masa grande. Esto resulta en reemplazar un radio circular, ${displaystyle r}$, con el eje semi-major, ${displaystyle a}$, del movimiento relativo elíptico de una masa relativa a la otra, así como la sustitución de la masa grande ${displaystyle M}$ con ${displaystyle M+m}$. Sin embargo, con las masas planetarias siendo mucho más pequeñas que el Sol, esta corrección es a menudo ignorada. La fórmula correspondiente completa es:

${displaystyle {frac {fnK}{2}={frac {G(M+m)}{4pi} ^{2}approx {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicros} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}}}}} {f}f} {f}f}f}f}f}f}f} {f}f} {f}f}fnMicrocfnMicrocf}f}f}f}f}fnMicrocfnMicrox}fnMicrocf}f} {fnKf}f}f}}f}}fnMicrocfnMicrocf}fnMicrocfnMicrocf}fnMi$

Donde ${displaystyle M}$ es la masa del Sol, ${displaystyle m}$ es la masa del planeta, ${displaystyle G.$ es la constante gravitacional, ${displaystyle T}$ es el período orbital y ${displaystyle a}$ es el eje semi-major elíptico, y ${displaystyle {text{AU}}}$ es la unidad astronómica, la distancia media de la tierra al sol.

Análisis dimensional

La tercera ley de Kepler puede derivarse con análisis dimensional utilizando la definición de fuerza como ${displaystyle T^{-2}LM}$ y la ley de gravedad de Newton que ${displaystyle F=Gm_{1}m_{2}/r^{2}$. Se puede utilizar la siguiente notación:

Signatura	Representación
${displaystyle F}$	la fuerza gravitatoria del cuerpo central, en este caso el Sol
${displaystyle l}$	eje semi-major del elipse de la órbita
${displaystyle m}$	masa del cuerpo orbital, en este caso el planeta
${displaystyle m_{s}$	masa del cuerpo central, en este caso la masa del Sol
${displaystyle t}$	el tiempo que el cuerpo toma para completar su órbita, en este caso el período de órbita planetaria

Entonces hay una función ${displaystyle t=f(F,m,l)}$ que se puede encontrar con el análisis dimensional. La siguiente tabla muestra cómo encontrar la forma no dimensional utilizando el análisis dimensional con el teorema de Buckingham Pi:

t	F	m	l
${displaystyle {Mathsf}}$	${displaystyle {Mathsf {2}LM}}$	${displaystyle {Mathsf}}$	${displaystyle {Mathsf}}$
	${displaystyle F*m^{-1}$
	${displaystyle {mathsf {2}L}}$
	${displaystyle F*m^{-1}*t^{2}$
	${displaystyle {Mathsf}}$
	${displaystyle F*m^{-1}*t^{2}*l^{-1}$
	1

Esto significa que la siguiente ecuación es verdadera:

${displaystyle F*m^{-1}*t^{2}*l^{-1}=constant}$

La ley de gravitación de Newton nos dice que

${displaystyle Fpropto m*m_{-2}$

Entonces esto se puede escribir como una ecuación:

${displaystyle ¿Qué?$

Las dos ecuaciones se pueden dividir entre sí. En el lado izquierdo hay

${displaystyle ¿Qué?$

Reordenando tenemos:

${displaystyle ¿Qué?$

Las variables ${displaystyle m}$ y ${displaystyle m_{s}$ ambos tienen la misma dimensión ${displaystyle {Mathsf}}$, que causa ${displaystyle ¿Qué?$ ser dimensionalmente equivalente a ${fnMicrosoft Sans} {fnMicrosoft Sans Ser} {f} {fnMicrosoft} {f}} {\fnMitsf}}} {fnMitsf}}} {fnMitsf} {f}}}} {\fnMitssf}}} {f}}}}}}}}}}}}}}} {m}}}}}}}} {m} {m} {m} {m} {m} {sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssoysssssssssssssssssssssssssssssssssssssssssssssssssssss {M}{-1+1}={mathsf {M} {0}=1}$. La dimensión de fuerza también cancela ${displaystyle F*F^{-1}$. Los únicos términos restantes ahora en el lado izquierdo son ${displaystyle ################################################################################################################################################################################################################################################################$. La ecuación es ahora ${displaystyle T^{2}*l^{-3}=constant}$. Esto prueba que ${displaystyle t^{2}propto l^{3}$. Así es como utilizar la ley de gravedad y análisis dimensional de Newton para derivar la tercera ley de Kepler.

Mesa

La siguiente tabla muestra los datos utilizados por Kepler para derivar empíricamente su ley:

Datos utilizados por Kepler (1618)

Planeta	Distancia media al sol (AU)	Período (días)	${textstyle {frac {}} {fn}} {fn}}} {fn}}}} {fn}}}}}} {fn}}}}}}}}}}}}}}}}}} {fn}} {}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}$(10)-6AU3Día2)
Mercurio	0,3989	87.77	7.64
Venus	0,724	224.70	7.52
Tierra	1	365.25	7.50
Marte	1.524	686.95	7.50
Júpiter	5.20	4332.62	7.49
Saturno	9.510	10759.2	7.43

Al encontrar este patrón, Kepler escribió:

Creía que estaba soñando... Pero es absolutamente cierto y exacto que la proporción que existe entre los tiempos de período de cualquier dos planetas es precisamente la proporción del 3/2 de poder de la distancia media.

—traducido del Armonías del Mundo por Kepler (1619)

Parcela de registro del período T vs semi-major axis a (promedio de aphelion y perihelion) de algunas órbitas del Sistema Solar (crudas que denotan los valores de Kepler) mostrando que a3/T2 es constante (línea verde)

A modo de comparación, aquí hay estimaciones modernas:

Datos modernos (Wolfram Alpha Knowledgebase 2018)

Planeta	Axis semi-major (AU)	Período (días)	${textstyle {frac {}} {fn}} {fn}}} {fn}}}} {fn}}}}}} {fn}}}}}}}}}}}}}}}}}} {fn}} {}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}$(10)-6AU3Día2)
Mercurio	0.38710	87.9693	7.496
Venus	0,7233	224.7008	7.496
Tierra	1	365.2564	7.496
Marte	1.52366	686.9796	7.495
Júpiter	5.20336	4332.8201	7.504
Saturno	9.53707	10775.599	7.498
Urano	19.1913	30687.153	7.506
Neptuno	30.0690	60190.03	7.504

Aceleración planetaria

Isaac Newton calculó en su Philosophiæ Naturalis Principia Mathematica la aceleración de un planeta que se mueve según la primera y la segunda ley de Kepler.

1. El dirección de la aceleración es hacia el Sol.
2. El magnitud de la aceleración es inversamente proporcional a la plaza de la distancia del planeta desde el Sol (el Derecho cuadrado inverso).

Esto implica que el Sol puede ser la causa física de la aceleración de los planetas. Sin embargo, Newton afirma en sus Principia que considera las fuerzas desde un punto de vista matemático, no físico, por lo que adopta una visión instrumentalista. Además, no asigna una causa a la gravedad.

Newton definió la fuerza que actúa sobre un planeta como el producto de su masa y la aceleración (consulte las leyes de movimiento de Newton). Asi que:

1. Cada planeta es atraído hacia el Sol.
2. La fuerza que actúa en un planeta es directamente proporcional a la masa del planeta y es inversamente proporcional a la plaza de su distancia del Sol.

El Sol juega un papel asimétrico, lo cual no está justificado. Así que asumió, en la ley de gravitación universal de Newton:

1. Todos los cuerpos del Sistema Solar se atraen unos a otros.
2. La fuerza entre dos cuerpos es en proporción directa al producto de sus masas y en proporción inversa a la plaza de la distancia entre ellos.

Como los planetas tienen masas pequeñas en comparación con la del Sol, las órbitas se ajustan aproximadamente a las leyes de Kepler. El modelo de Newton mejora el modelo de Kepler y se ajusta a las observaciones reales con mayor precisión. (Ver problema de dos cuerpos).

A continuación se muestra el cálculo detallado de la aceleración de un planeta que se mueve según la primera y la segunda ley de Kepler.

Vector de aceleración

Desde el punto de vista heliocéntrico considerar el vector al planeta ${displaystyle mathbf {r} =r{hat {mathbf {r}}} {f}$ Donde ${displaystyle r}$ es la distancia al planeta y ${fnMicrosoft Sans Serif} }$ es un vector unitario apuntando hacia el planeta.

$${displaystyle {frac {fnK} {fnMitbf} {fnK} {fnh} {fnh}} {fnh} {fnh}} {f} {fn}} {fn} {fnf}} {fn}}} {fn} {f}}}} {f} {f}}} {fnf} {f}}}} {f} {f}}}} {f}}} {f}}}} {f}}}} {f}}}}}}}}}} {f} {f} {f} {f} {f} {f}}} {f}}}}} {f} {f} {f}}} {f}} {f} {f}} {f}}}}f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}} }={dot {theta }{hat {boldsymbol {theta}}qquad {frac {fnha {fnMicrosoft {fnMicrosoft} {}} {}}={dot {ha {fnfnMicrosoft {fnMicrosoft} }=-{dot {theta - Sí.$$

Donde ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\f}fnMicrosoft {\\\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\\\\\fnMicrosoft {fnMicrosoft }$ es el vector de unidad cuya dirección es de 90 grados en sentido contrario ${fnMicrosoft Sans Serif} }$, y ${displaystyle theta }$ es el ángulo polar, y donde un punto en la parte superior de la variable significa diferenciación con respecto al tiempo.

Diferencie el vector de posición dos veces para obtener el vector de velocidad y el vector de aceleración:

$${fnMitbf {}} {fnK}} {fn}} {fn}} {fn} {fn}} {fn}}} {fnfn} {fn}}} {fn}}}}} {fnf}}}} {fnfnf}}}} {f}}}}}}}}}}} {f}}}}}} {f}}}}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}} {f}}}} {f} {f} {f} {f}}} {f}}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} ¿Qué? }={dot {} {hat {mathbf {r} }+r{dot {theta {fnK} {fnMitbf {fnK}}\fnMitbf {f} {fnh}fnh} {fnh} {fnh}fnhfnh}+ {fnh} {fnh} {fnh}}}nh}nhnhnh}nhnh}hnhnh}nhhhnhhhnhhhhhnhhhhh}hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh }{hat {boldsymbol {theta }+r{ddot {theta }{hat {boldsymbol {theta {fnfnfnh} {fnfnfnfnhfnhfnfnK}}}r {dot {theta} {fnh} {fnfnfnfnfnh} {fnfnh} {fnfnfnfnfnh}}}}}}}}} {f}}}}}}}}}}}}}}}nns\s\\\nh}t {nns}t {hns}}}t {h}t {hns}}}}}t {h}}}}}}}}}nnnnnnnnn}}t {h}}}n}}}}}nnnnnnnnnnnn - Sí. {fnMicrosoft Sans Serif} {fnMicrosoft}fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {f}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}fnMicros}}}} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnun}f}f}f}f}f}f}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}}fnun}fnun} {fnun}fn {fnMicrosoft Sans Serif}$$

Entonces

$${displaystyle {ddot {fnMitbf} }=a_{r} {hat {boldsymbol {fnh}+a_{theta } {hat {boldsymbol {theta }$$

$${displaystyle A_{r}={ddot {r}-r{dot {theta } {2}$$

$${displaystyle a_{theta - ¿Qué? }}$$

Ley del cuadrado inverso

La segunda ley de Kepler dice que

$${displaystyle r^{2}{dot {theta }=nab}$$

La aceleración transversal ${displaystyle a_{theta }$ es cero:

$${displaystyle {frac {dleft(r^{2}{dot {theta }right)}{dt}}=rleft(2{dot {fnK} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}} {fn}} {fn}}} {fnMicrosoft}}} {fn}} {f}} {f}}}} {fnMis}}} {f}}}} {f} {f}}}} {f}}}} {f} {f}}f}}}}f}f}f} {f} }+r{ddot {theta - Sí. }=0.}$$

Entonces, la aceleración de un planeta que obedece la segunda ley de Kepler está dirigida hacia el Sol.

La aceleración radial ${displaystyle a_{text{r}}$ es

$${displaystyle a_{text{r}={ddot {R}-r{dot {theta {fnMicroc {fnK}}}derecho)}={ddot {r}-{frac} {n^{2}a} {2}}} {r^{3}}}} {cH00}} {cH00}}} {ccH00}}}} {cH00}}}}}}}}}} {ccH00}}}}$$

La primera ley de Kepler establece que la órbita se describe mediante la ecuación:

$${displaystyle {frac {}=1+varepsilon cos(theta).}$$

Derivar con respecto al tiempo

$${displaystyle - ¿Qué? {}}{2}}=-varepsilon sin(theta),{dot {theta] }$$

$${displaystyle p{dot {r}=nab,varepsilon sin(theta).}$$

Diferenciando una vez más

$${displaystyle p{ddot {}=nabvarepsilon cos(theta),{dot {theta] }=nabvarepsilon cos(theta),{frac {nab}{2}}}={frac {n^{2}a^{2} {2}}varepsilon cos(theta).}$$

La aceleración radial ${displaystyle a_{text{r}}$ satisfizo

$${displaystyle pa_{text{r}}={frac {2}a^{2}b^{2}}{2}}}varepsilon cos(theta)-p{frac} {fn}} {c}}}}}}varepsilon cos(theta)-p{f} {n^{2}a^{2}{2}}}={frac {n^{2}a} {2}b^{2}}} {r^{2}}}}left(varepsilon cos(theta)-{frac {r} {r}}right).}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$$

Sustituyendo la ecuación de la elipse da

$${displaystyle pa_{text{}}={frac {2}a}b^{2}}{2}}}}}left({frac} {f} {f}}}} {fn}}}}}}}}m} {f} {f} {f} {fnf}f}}}}}}}}}}}}}}}}}}}f}}}}}}}m}}}}}}}}}m}m}}}}m}m}}}m}m}}}}m}}}}}}}}}m} {f}}}m}m}}}m}m}}m}m}m}m}m}m}m}m}m} {m}m}m} {m}m}}m}}}}m}}}}m}m} {p} {r}-1-{frac} {p} {r}right)=-{frac {n^{2}a} {r^{2}}b^{2}}$$

La relación ${displaystyle b^{2}=pa}$ da el resultado final simple

$${displaystyle a_{text{r}=-{frac {n^{2}a} {r^{2}}}}$$

Esto significa que el vector de aceleración ${displaystyle mathbf {ddot {r}$ de cualquier planeta obedeciendo la primera y segunda ley de Kepler satisfice la Derecho cuadrado inverso

$${displaystyle mathbf {ddot {r} {fnh} {fnh}} {fnh}}}$$

$${displaystyle alpha =n^{2}a^{3}$$

${fnMicrosoft Sans Serif} }$

${displaystyle r,}$

Desde la moción media ${displaystyle n={frac {2pi}{T}} {f}} {f}} {f}} {f}} {f}}}$ Donde ${displaystyle T}$ es el período, según la tercera ley de Kepler, ${displaystyle alpha }$ tiene el mismo valor para todos los planetas. Así que la inversa ley cuadrada para las aceleraciones planetarias se aplica en todo el Sistema Solar.

La ley del cuadrado inverso es una ecuación diferencial. Las soluciones a esta ecuación diferencial incluyen los movimientos keplerianos, como se muestra, pero también incluyen movimientos en los que la órbita es una hipérbola, una parábola o una línea recta. (Ver órbita de Kepler).

La ley de gravitación de Newton

Por la segunda ley de Newton, la fuerza gravitatoria que actúa sobre el planeta es:

$${displaystyle mathbf {F} =m_{text{planet}mathbf {ddot {r} =-m_{text{planet}alpha {fnK}$$

Donde ${displaystyle m_{text{planet}}$ es la masa del planeta y ${displaystyle alpha }$ tiene el mismo valor para todos los planetas del Sistema Solar. Según la tercera ley de Newton, el Sol es atraído al planeta por una fuerza de la misma magnitud. Puesto que la fuerza es proporcional a la masa del planeta, bajo la consideración simétrica, también debe ser proporcional a la masa del Sol, ${displaystyle m_{text{Sun}}$. Así que...

$${displaystyle alpha =Gm_{text{Sun}}$$

${displaystyle G.$

La aceleración del cuerpo del sistema solar número i es, según las leyes de Newton:

$${displaystyle mathbf {ddot {r} _{i}=Gsum _{jneq {fnMicrosoft Sans Serif} - Sí.$$

${displaystyle #$

${displaystyle r_{ij}$

${fnMicrosoft Sans Serif} - Sí.$

En el caso especial en el que solo hay dos cuerpos en el Sistema Solar, la Tierra y el Sol, la aceleración se convierte en

$${displaystyle mathbf {ddot {r} {text{f}=Gm_{text{Sun}r_{text{f}} {text{f}}} {text{sun}}}{-2}{hat {mathbf {r}}}} {f}} {f}}}} {f}}} {f}}} {f}} {f}}} {f}}} {f}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}} {f}} {f} {f} {f} {f} {f} {f} {f} {f} {f}f} {f}f}f} {f}f}f}f}f}f}}f}}}}f}f}f}}f} } {text{f}} {text{sun}}}$$

Si los dos cuerpos del Sistema Solar son la Luna y la Tierra, la aceleración de la Luna se convierte en

$${displaystyle mathbf {ddot {r} {text{Moon}=Gm_{text{Earth}r_{text{Moon}} {text{Earth}}}{-2}{hat {hat {mathbf {r}}}} {f}}} {f}}} {f}}}}} {f}}}}} {f} {f}} {f}}}}} {f}}} {f}} {f}}}} {f}}}}} {f}}}}}}}f}}}}}}}}}}}}}}} {f} {f} {f} {f} {f} {f} {f} {f} {f}f} {f}f}}f}f}f}f}f}f}f}f}f}}}}}}} {fnMicrosoft} {fnMicrosoft}}$$

Entonces, en esta aproximación, la Luna se mueve alrededor de la Tierra según las leyes de Kepler.

En el caso de tres cuerpos las aceleraciones son

$${displaystyle {begin{aligned}mathbf {ddot {r} _{text{Sun} {f}} {text{f}}r_{text{sun}} {text{f}}} {f} {f} {f}} {f}}} {f}f}f}}}}} {f} {f}}}}f}}}}}f}f}}f}}}f}f}f}f}}}f}}}}f}}}}}}f}}}}}}}}}}}}}}}}}} {f}}}} {f} {f} {f}f} {f} {f}f}f}}}}f}}}}}}}}f}f}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {f}} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}}} {f} {fnMitbf {f}}}}} {f}f}f}f} {f}f}f}f}f}}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnfnf}f}f}f}f}f}}}f}fn {fnh}\fnh}\\fnh}\\fnh}\mfnh}} {text{f}}}} {fn}}} {fn}fnh}}} {mfnh}} {f}f}}f}fnf} {f}f}}}}f}f}}f}f}}f}f}f}}}}}\f}f}}\\f}}\\f}\\f}\\\\\f}\\\fn\\\f}fnh}f}\\\\\\f}\\\\\\fnfn\\fn\\\\fnh}\\\ {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {f}} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}}} {f} {fnMitbf {f}}}} {f}f}}f}}}} {f}f}f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}f}}f}f}f}}f}f}f}f}f}f}f}}}f}}}}}f}f}f}f}f}f}f}f}f}fnfnfnf}}}f}}}}}f}}}}}}}fn {fnMicrosoft} {fnK}\fnh}\\fnh} {fnh} {f}}} {text{m}}}} {text{fn}} {fnf}} {mf}}} {f} {f}}}f}}}} {f} {f}f}f}f}}}}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}}}f}f}f}}f}}}}}}}}}f} {f}f}}}f}}}}}}f}}}}f}\\f}f}}}f}}}}}}f}f}f}}}}}}}}}}f}f}}}}}}} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}} {f}} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f} {fnMitbf {f}}}}} {f}f}}f}}f}}f}f}f}f}f}f}f}}f}f}f} {f}f} {f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}fnf}fnf}f}f}}}f}f}}}}}fn {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}}$$

Estas aceleraciones no son las de las órbitas de Kepler, y el problema de los tres cuerpos es complicado. Pero la aproximación Kepleriana es la base para los cálculos de perturbaciones. (Ver teoría lunar).

Posición en función del tiempo

Kepler utilizó sus dos primeras leyes para calcular la posición de un planeta en función del tiempo. Su método implica la solución de una ecuación trascendental llamada ecuación de Kepler.

El procedimiento para calcular las coordenadas polares heliocéntricas (r,θ) de un planeta en función del tiempo t desde el perihelio, son los siguientes cinco pasos:

1. Computar el movimiento n = 2π rad)/P, donde P es el período.
2. Computar el anomalía M = nt, donde t es el momento desde el perihelio.
3. Computar el anomalía excéntrica E resolviendo la ecuación de Kepler:
   $${displaystyle M=E-varepsilon sin E,}$$

   
   Donde ${displaystyle varepsilon }$ es la excentricidad.
4. Computar el verdadera anomalía Silencio resolver la ecuación:
   $${displaystyle (1-varepsilon)tan ^{2}{frac {theta {2}=(1+varepsilon)tan ^{2}{2}}}$$

   
5. Computar el distancia heliocéntrico r:
   $${displaystyle r=a(1-varepsilon cos E),}$$

   
   Donde ${displaystyle a}$ es el eje semimajor.

El vector de velocidad cartesiana se puede calcular como ${displaystyle mathbf {v} ={frac {sqrt {mu} a} {r}leftlangle -sin {E},{sqrt {1-varepsilon. Está bien.$, donde ${displaystyle mu }$ es el parámetro gravitacional estándar.

El importante caso especial de órbita circular, ε = 0, da θ = E = < i>M. Debido a que el movimiento circular uniforme se consideró normal, una desviación de este movimiento se consideró una anomalía.

La prueba de este procedimiento se muestra a continuación.

Anomalía media, M

Figura 5: Construcción geométrica para el cálculo de Kepler de θ. El Sol (ubicado en el foco) está etiquetado S y el planeta P. El círculo auxiliar es una ayuda para calcular. Línea xd es perpendicular a la base y a través del planeta P. Los sectores sombreados están dispuestos a tener áreas iguales al posicionamiento de punto Sí..

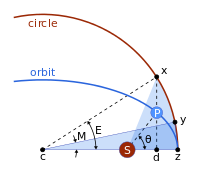
El problema de Kepler asume una órbita elíptica y los cuatro puntos:

• s el Sol (en un foco de elipse);
• z el perihelio
• c el centro de la elipse
• p el planeta

y

• ${displaystyle a=persecuentes vidas,}$ distancia entre centro y perihelio, el semimajor axis,
• ${displaystyle varepsilon ={ torturas vivas over a},}$ el excentricidad,
• ${displaystyle b=a{sqrt {1-varepsilon }}}}$ el semiminor axis,
• ${displaystyle r= impertinentes,}$ la distancia entre Sol y planeta.
• ${displaystyle theta =angle zsp,}$ la dirección al planeta como se ve desde el Sol, el verdadera anomalía.

El problema es calcular las coordenadas polares (r,θ) del planeta a partir del tiempo transcurrido desde el perihelio, t .

Se resuelve en pasos. Kepler consideró el círculo con el eje mayor como un diámetro, y

• ${displaystyle x,}$ la proyección del planeta al círculo auxiliar
• ${displaystyle y,}$ el punto en el círculo de tal manera que las áreas del sectorzcySilencio y sufrimientozsx.
• ${displaystyle M=angle zcy,}$ el anomalía.

Las esferas del sector están relacionadas ${fnMicrosoft Sans Serif}cdot Silencioso.$

El sector circular ${fnMicrosoft Sans Serif} {a^{2}M} {2}}}$

El área barrida desde el perihelio,

$${fnMicrosoft Sans}cdot Silencioso {b}{a}cdot {b}}cdot {a} {2}={frac {abM}{2}}}} {f} {f}} {f}} {fn}}}$$

$${displaystyle M=nt,}$$

Anomalía excéntrica, E

Cuando se calcula la anomalía media M, el objetivo es calcular la anomalía verdadera θ. Sin embargo, la función θ = f(M) no es elemental. La solución de Kepler es usar

$${displaystyle E=angle zcx,}$$

$${displaystyle {begin{aligned}Prince {begin{fnMicrosoft Prision} {2} {2}} {2}}}} {frac {2} {2}} {frac {avarepsilon cdot asin} E} {2}end{aligned}}$$

La división por a²/2 da la ecuación de Kepler

$${displaystyle M=E-varepsilon sin E.}$$

Esta ecuación da M como una función de E. Determinar E para un M dado es el problema inverso. Los algoritmos numéricos iterativos se utilizan comúnmente.

Habiendo calculado la anomalía excéntrica E, el siguiente paso es calcular la anomalía real θ.

Pero tenga en cuenta: las coordenadas de posición cartesianas con referencia al centro de la elipse son (a cos E, b sin E< /i>)

Con referencia al Sol (con coordenadas (c,0) = (ae,0)), r = (a cos E – ae, b sin E)

La verdadera anomalía sería arctan(r_y/rx), la magnitud de r sería √r · r.

Verdadera anomalía, θ

Observe en la figura que

$${fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\\fnMicro {fnMicro {fnMicrosoft {fnMicro {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicro {fnMicrosoft {fnMicrosoft {fnMicro {fnMicrosoft {fnMicro {cd}={overrightarrow {cs}+{overrightarrow {}}$$

$${displaystyle acos E=avarepsilon +rcos theta.}$$

Dividiendo por ${displaystyle a}$ e inserción de la primera ley de Kepler

$${fnMicroc} {} {fn}={fnMic} {1-varepsilon ^{2}{1+varepsilon cos theta }$$

$${displaystyle cos E=varepsilon +{frac {1-varepsilon ^{2}{1+varepsilon cos theta } cos theta ={frac {varepsilon (1+varepsilon cos theta)+left(1-varepsilon ^{2}right)cos theta }{1+varepsilon cos theta }={frac {varepsilon +cos theta }{1+varepsilon cos theta }}$$

El resultado es una relación utilizable entre la anomalía excéntrica E y la anomalía verdadera θ.

Se sigue una forma computacionalmente más conveniente al sustituir en la identidad trigonométrica:

$${displaystyle tan ^{2}{frac} {x}{2}={frac} {1-cos x}{1+cos x}}$$

Obtener

$${displaystyle {begin{aligned}tan {E}{2} {1-cos E}{1+cos E}={frac {1-{frac {varepsilon +cos theta }{1+varepsilon cos theta {}}{1+{frac {varepsilon +cos theta }{1+varepsilon cos theta {1+varepsilon cos theta)-(varepsilon +cos theta)}{(1+varepsilon cos theta)}{(1+varepsilon cos theta)+(varepsilon +cos theta)}={frac {1-varepsilon }{1+varepsilon }cdot {frac {1-cos theta }{1+cos theta }={frac {1-varepsilon {1+varepsilon}tan ^{2}{2} {theta }}end{aligned}}$$

Multiplicar por 1 + ε da el resultado

$${displaystyle (1-varepsilon)tan ^{2}{frac {theta {2}=(1+varepsilon)tan ^{2}{2}}}$$

Este es el tercer paso en la conexión entre el tiempo y la posición en la órbita.

Distancia, r

El cuarto paso es calcular la distancia heliocéntrica r desde la anomalía verdadera θ mediante la primera ley de Kepler:

$${displaystyle r(1+varepsilon cos theta)=aleft(1-varepsilon ^{2}right)}$$

Usando la relación anterior entre θ y E, la ecuación final para la distancia r es:

$${displaystyle r=a(1-varepsilon cos E).}$$

Notas explicativas