Ley de Planck

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Densidad espectral de luz emitida por un cuerpo negro

La ley de Planck describe con precisión la radiación del cuerpo negro. Aquí se muestra una familia de curvas para diferentes temperaturas. La curva clásica (negro) se desprende de la intensidad observada a altas frecuencias (longitudes cortas de onda).

En física, la ley de Planck describe la densidad espectral de la radiación electromagnética emitida por un cuerpo negro en equilibrio térmico a una temperatura dada $T$ , cuando no hay un flujo neto de materia o energía entre el cuerpo y su entorno.

A fines del siglo XIX, los físicos no pudieron explicar por qué el espectro observado de radiación de cuerpo negro, que para entonces se había medido con precisión, divergía significativamente en frecuencias más altas de lo previsto por las teorías existentes. En 1900, el físico alemán Max Planck derivó heurísticamente una fórmula para el espectro observado asumiendo que un hipotético oscilador cargado eléctricamente en una cavidad que contenía radiación de cuerpo negro solo podía cambiar su energía en un incremento mínimo, $E$ , que era proporcional a la frecuencia de su onda electromagnética asociada. Si bien Planck originalmente consideró la hipótesis de dividir la energía en incrementos como un artificio matemático, introducido simplemente para obtener la respuesta correcta, otros físicos, incluido Albert Einstein, se basaron en su trabajo, y ahora se reconoce que la idea de Planck es de importancia fundamental para Teoría cuántica.

La ley

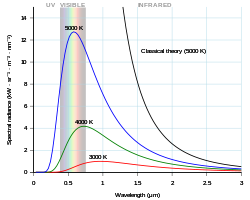
Todo cuerpo físico emite espontánea y continuamente radiación electromagnética y la radiación espectral de un cuerpo, $B ν$ , describe la potencia emisiva espectral por unidad de área, por unidad de ángulo sólido, por unidad de frecuencia para frecuencias de radiación particulares. La relación dada por la ley de radiación de Planck, que se muestra a continuación, muestra que con el aumento de la temperatura, la energía total radiada de un cuerpo aumenta y el pico del espectro emitido se desplaza hacia longitudes de onda más cortas. Según esto, la radiación espectral de un cuerpo para la frecuencia $ν$ a temperatura absoluta $T$ viene dado por

{displaystyle B_{nu }(nuT)={frac {2hnu ^{3}}{c^{2}}}{frac {1}{exp left({frac {hnu }{k_{mathrm {B} }T}}right)-1}},}

k B

h

c

B .

W·sr⁻¹·m⁻²·Hz⁻¹

La radiación espectral también se puede expresar por unidad de longitud de onda $λ$ en lugar de por unidad de frecuencia. Además, la ley puede expresarse en otros términos, como el número de fotones emitidos a una determinada longitud de onda o la densidad de energía en un volumen de radiación.

En el límite de frecuencias bajas (es decir, longitudes de onda largas), la ley de Planck tiende a la ley de Rayleigh-Jeans, mientras que en el límite de frecuencias altas (es decir, longitudes de onda pequeñas) tiende a la aproximación de Wien.

Max Planck desarrolló la ley en 1900 solo con constantes determinadas empíricamente y luego demostró que, expresada como una distribución de energía, es la única distribución estable para la radiación en equilibrio termodinámico. Como distribución de energía, pertenece a una familia de distribuciones de equilibrio térmico que incluyen la distribución de Bose-Einstein, la distribución de Fermi-Dirac y la distribución de Maxwell-Boltzmann.

Radiación de cuerpo negro

El Sol aproxima un radiador de cuerpo negro. Su temperatura efectiva es sobre 5777 K.

Un cuerpo negro es un objeto idealizado que absorbe y emite todas las frecuencias de radiación. Cerca del equilibrio termodinámico, la radiación emitida está estrechamente descrita por la ley de Planck y, debido a su dependencia de la temperatura, se dice que la radiación de Planck es radiación térmica, de modo que cuanto mayor es la temperatura de un cuerpo, más radiación emite en cada momento. longitud de onda.

La radiación de Planck tiene una intensidad máxima en una longitud de onda que depende de la temperatura del cuerpo. Por ejemplo, a temperatura ambiente (~300 K), un cuerpo emite radiación térmica que es principalmente infrarroja e invisibles. A temperaturas más altas, la cantidad de radiación infrarroja aumenta y se puede sentir como calor, y se emite más radiación visible para que el cuerpo brille visiblemente rojo. A temperaturas más altas, el cuerpo es de color amarillo brillante o blanco azulado y emite cantidades significativas de radiación de longitud de onda corta, incluidos los rayos ultravioleta e incluso los rayos X. La superficie del sol (~6000 K) emite grandes cantidades de radiación infrarroja y ultravioleta; su emisión alcanza su punto máximo en el espectro visible. Este cambio debido a la temperatura se llama ley de desplazamiento de Wien.

La radiación de Planck es la mayor cantidad de radiación que cualquier cuerpo en equilibrio térmico puede emitir desde su superficie, cualquiera que sea su composición química o estructura superficial. El paso de la radiación a través de una interfaz entre los medios se puede caracterizar por la emisividad de la interfaz (la relación entre la radiación real y la radiación de Planck teórica), generalmente denotada por el símbolo $ε$ . En general, depende de la composición química y la estructura física, de la temperatura, de la longitud de onda, del ángulo de paso y de la polarización. La emisividad de una interfaz natural siempre está entre $ε$ = 0 y 1.

Un cuerpo que interactúa con otro medio que tiene $ε$ = 1 y absorbe todo la radiación que incide sobre él se dice que es un cuerpo negro. La superficie de un cuerpo negro se puede modelar mediante un pequeño orificio en la pared de un recinto grande que se mantiene a una temperatura uniforme con paredes opacas que, en todas las longitudes de onda, no son perfectamente reflectantes. En equilibrio, la radiación dentro de este recinto está descrita por la ley de Planck, al igual que la radiación que sale del pequeño agujero.

Así como la distribución de Maxwell-Boltzmann es la única distribución de energía de máxima entropía para un gas de partículas materiales en equilibrio térmico, también lo es la distribución de Planck para un gas de fotones. A diferencia de un gas material en el que las masas y el número de partículas juegan un papel, la radiación espectral, la presión y la densidad de energía de un gas fotónico en equilibrio térmico están totalmente determinadas por la temperatura.

Si el gas fotónico no es planckiano, la segunda ley de la termodinámica garantiza que las interacciones (entre fotones y otras partículas o incluso, a temperaturas suficientemente altas, entre los mismos fotones) harán que la distribución de la energía fotónica cambie y se acerque a Planck. distribución. En tal enfoque del equilibrio termodinámico, los fotones se crean o aniquilan en el número correcto y con las energías correctas para llenar la cavidad con una distribución de Planck hasta que alcanzan la temperatura de equilibrio. Es como si el gas fuera una mezcla de subgases, uno para cada banda de longitudes de onda, y cada subgas finalmente alcanza la temperatura común.

La cantidad $B ν (ν, T)$ es la radiación espectral en función de la temperatura y la frecuencia. Tiene unidades de W·m⁻²·sr⁻¹·Hz⁻¹ en el sistema SI. Una cantidad infinitesimal de energía $B ν (ν, T) cos θ dA d Ω dν$ se radia en la dirección descrita por el ángulo $θ$ desde la superficie normal desde el área de superficie infinitesimal $dA$ en un ángulo sólido infinitesimal $d Ω$ en una banda de frecuencia infinitesimal de ancho $dν$ centrado en la frecuencia $ν$ . La potencia total radiada en cualquier ángulo sólido es la integral de $B ν (ν, T)$ sobre esas tres cantidades, y está dada por la ley de Stefan-Boltzmann. El resplandor espectral de la radiación planckiana de un cuerpo negro tiene el mismo valor para todas las direcciones y ángulos de polarización, por lo que se dice que el cuerpo negro es un radiador lambertiano.

Diferentes formas

La ley de Planck se puede encontrar en varias formas según las convenciones y preferencias de los diferentes campos científicos. Las diversas formas de la ley de radiación espectral se resumen en la siguiente tabla. Las formas de la izquierda se encuentran con mayor frecuencia en campos experimentales, mientras que las de la derecha se encuentran con mayor frecuencia en campos teóricos.

Ley de Planck expresada en términos de diferentes variables espectrales
con $h$		con $▪$
variable	distribución	variable	distribución
Frecuencia $.$	${displaystyle B_{nu }(nuT)={frac {2hnu ^{3}}{c^{2}}}{frac {1}{e^{hnu /(k_{mathrm {B} }T)}-1}}}$	Frecuencia angular $\cdot$	$B_{omega }(omegaT)={frac {hbar omega ^{3}}{4pi ^{3}c^{2}}}{frac {1}{e^{hbar omega /(k_{mathrm {B} }T)}-1}}$
Wavelength $λ$	${displaystyle B_{lambda }(lambdaT)={frac {2hc^{2}}{lambda ^{5}}}{frac {1}{e^{hc/(lambda k_{mathrm {B} }T)}-1}}}$	Longitud de onda angular $Sí.$	${displaystyle B_{y}(y,T)={frac {hbar c^{2}}{4pi ^{3}y^{5}}}{frac {1}{e^{hbar c/(yk_{mathrm {B} }T)}-1}}}$
Número de onda $♪$	${displaystyle B_{tilde {nu }}({tilde {nu }},T)=2hc^{2}{tilde {nu }}^{3}{frac {1}{e^{hc{tilde {nu }}/(k_{mathrm {B} }T)}-1}}}$	Número de onda angular $k$	${displaystyle B_{k}(k,T)={frac {hbar c^{2}k^{3}}{4pi ^{3}}}{frac {1}{e^{hbar ck/(k_{mathrm {B} }T)}-1}}}$

Estas distribuciones representan la radiación espectral de los cuerpos negros: la potencia emitida desde la superficie emisora, por unidad de área proyectada de superficie emisora, por unidad de ángulo sólido, por unidad espectral (frecuencia, longitud de onda, número de onda o sus equivalentes angulares). Dado que la radiación es isotrópica (es decir, independiente de la dirección), la potencia emitida en un ángulo con respecto a la normal es proporcional al área proyectada y, por lo tanto, al coseno de ese ángulo según la ley del coseno de Lambert, y no está polarizada.

Correspondencia entre formas de variables espectrales

Diferentes variables espectrales requieren diferentes formas correspondientes de expresión de la ley. En general, uno no puede convertir entre las distintas formas de la ley de Planck simplemente sustituyendo una variable por otra, porque esto no tendría en cuenta que las diferentes formas tienen diferentes unidades. Las unidades de longitud de onda y frecuencia son recíprocas.

Las formas de expresión correspondientes están relacionadas porque expresan el mismo hecho físico: para un incremento espectral físico particular, se irradia un incremento de energía física particular correspondiente.

Esto es así ya sea que se exprese en términos de un incremento de frecuencia, $d ν$ , o, correspondientemente, de longitud de onda, $d λ$ . La introducción de un signo menos puede indicar que un incremento de frecuencia se corresponde con una disminución de la longitud de onda. Para convertir las formas correspondientes para que expresen la misma cantidad en las mismas unidades multiplicamos por el incremento espectral. Entonces, para un incremento espectral particular, el incremento de energía física particular puede escribirse

{displaystyle B_{lambda }(lambdaT),dlambda =-B_{nu }(nu (lambda),T),dnu}

{displaystyle B_{lambda }(lambdaT)=-{frac {dnu }{dlambda }}B_{nu }(nu (lambda),T).}

Además, $ν (λ) = c / λ$ , de modo que $dν / dλ = - c / λ 2$ . La sustitución da la correspondencia entre las formas de frecuencia y longitud de onda, con sus diferentes dimensiones y unidades. Como consecuencia,

{displaystyle {frac {B_{lambda }(T)}{B_{nu }(T)}}={frac {c}{lambda ^{2}}}={frac {nu ^{2}}{c}}.}

Evidentemente, la ubicación del pico de la distribución espectral de la ley de Planck depende de la elección de la variable espectral. Sin embargo, por así decirlo, esta fórmula significa que la forma de la distribución espectral es independiente de la temperatura, según la ley de desplazamiento de Wien, como se detalla más adelante en la subsección Percentiles de la sección Propiedades.

Forma de densidad de energía espectral

La ley de Planck también se puede escribir en términos de densidad de energía espectral ( $u$ ) multiplicando $B$ por $4π / c$ :

{displaystyle u_{i}(T)={frac {4pi }{c}}B_{i}(T).}

Estas distribuciones tienen unidades de energía por volumen por unidad espectral.

Constantes de radiación primera y segunda

En las variantes anteriores de la ley de Planck, las variantes longitud de onda y número de onda usan los términos $2 hc 2$ y $hc / k B$ que comprenden solo constantes físicas. En consecuencia, estos términos pueden considerarse constantes físicas en sí mismos y, por lo tanto, se denominan la primera constante de radiación $c 1 L$ y la segunda constante de radiación $c 2$ con

c 1 L = 2 hc 2

c 2 = hc / k B

Usando las constantes de radiación, la variante longitud de onda de la ley de Planck se puede simplificar a

{displaystyle L(lambdaT)={frac {c_{1L}}{lambda ^{5}}}{frac {1}{exp left({frac {c_{2}}{lambda T}}right)-1}}}

número de onda

$L$ se usa aquí en lugar de $B$ porque es el símbolo SI para radiancia espectral. La $L$ en $c 1 L$ se refiere a eso. Esta referencia es necesaria porque la ley de Planck se puede reformular para dar una salida radiante espectral $M (λ, T)$ en lugar de resplandor espectral $L (λ, T)$ , en cuyo caso $c 1$ reemplaza a $c 1 L$ , con

c 1 = 2π hc 2

de modo que la ley de Planck para la salida radiante espectral se puede escribir como

{displaystyle M(lambdaT)={frac {c_{1}}{lambda ^{5}}}{frac {1}{exp left({frac {c_{2}}{lambda T}}right)-1}}}

Como las técnicas de medición han mejorado, la Conferencia General de Pesos y Medidas ha revisado su estimación de $c 2$ ; consulte Lugar geométrico de Planckian § Escala internacional de temperatura para obtener más detalles.

Física

Congelación de osciladores de alta energía

La ley de Planck describe la distribución espectral única y característica de la radiación electromagnética en equilibrio termodinámico, cuando no hay un flujo neto de materia o energía. Su física se comprende más fácilmente considerando la radiación en una cavidad con paredes rígidas y opacas. El movimiento de las paredes puede afectar la radiación. Si las paredes no son opacas, entonces el equilibrio termodinámico no está aislado. Es de interés explicar cómo se alcanza el equilibrio termodinámico. Hay dos casos principales: (a) cuando la aproximación al equilibrio termodinámico es en presencia de materia, cuando las paredes de la cavidad son imperfectamente reflectantes para cada longitud de onda o cuando las paredes son perfectamente reflectantes mientras que la cavidad contiene un pequeño cuerpo negro (este fue el caso principal considerado por Planck); o (b) cuando la aproximación al equilibrio es en ausencia de materia, cuando las paredes reflejan perfectamente todas las longitudes de onda y la cavidad no contiene materia. Para la materia que no está encerrada en tal cavidad, la radiación térmica puede explicarse aproximadamente mediante el uso apropiado de la ley de Planck.

La física clásica condujo, a través del teorema de equipartición, a la catástrofe ultravioleta, una predicción de que la intensidad total de la radiación del cuerpo negro era infinita. Si se complementa con la suposición clásicamente injustificable de que, por alguna razón, la radiación es finita, la termodinámica clásica proporciona una explicación de algunos aspectos de la distribución de Planck, como la ley de Stefan-Boltzmann y la ley de desplazamiento de Wien. Para el caso de la presencia de materia, la mecánica cuántica proporciona una buena explicación, como se encuentra más adelante en la sección titulada Coeficientes de Einstein. Este fue el caso considerado por Einstein, y hoy en día se utiliza para la óptica cuántica. Para el caso de la ausencia de materia, es necesaria la teoría cuántica de campos, porque la mecánica cuántica no relativista con números de partículas fijos no proporciona una explicación suficiente.

Fotones

La explicación teórica cuántica de la ley de Planck considera que la radiación es un gas de partículas bosónicas sin carga y sin masa, es decir, fotones, en equilibrio termodinámico. Los fotones son vistos como los portadores de la interacción electromagnética entre partículas elementales cargadas eléctricamente. Los números de fotones no se conservan. Los fotones se crean o aniquilan en los números correctos y con las energías adecuadas para llenar la cavidad con la distribución de Planck. Para un gas fotónico en equilibrio termodinámico, la densidad de energía interna está completamente determinada por la temperatura; además, la presión está totalmente determinada por la densidad de energía interna. Esto es diferente al caso del equilibrio termodinámico para gases materiales, para los cuales la energía interna está determinada no solo por la temperatura, sino también, independientemente, por el número respectivo de las diferentes moléculas, e independientemente nuevamente, por las características específicas de los diferentes. moléculas. Para diferentes gases materiales a una temperatura dada, la presión y la densidad de energía interna pueden variar independientemente, porque diferentes moléculas pueden transportar independientemente diferentes energías de excitación.

La ley de Planck surge como un límite de la distribución de Bose-Einstein, la distribución de energía que describe bosones no interactivos en equilibrio termodinámico. En el caso de bosones sin masa, como fotones y gluones, el potencial químico es cero y la distribución de Bose-Einstein se reduce a la distribución de Planck. Existe otra distribución de energía de equilibrio fundamental: la distribución de Fermi-Dirac, que describe los fermiones, como los electrones, en equilibrio térmico. Las dos distribuciones difieren porque múltiples bosones pueden ocupar el mismo estado cuántico, mientras que múltiples fermiones no pueden. A bajas densidades, el número de estados cuánticos disponibles por partícula es grande y esta diferencia se vuelve irrelevante. En el límite de baja densidad, las distribuciones de Bose-Einstein y Fermi-Dirac se reducen a la distribución de Maxwell-Boltzmann.

Ley de radiación térmica de Kirchhoff

La ley de radiación térmica de Kirchhoff es una explicación sucinta y breve de una situación física complicada. El siguiente es un bosquejo introductorio de esa situación, y está muy lejos de ser un argumento físico riguroso. El propósito aquí es solo resumir los principales factores físicos en la situación y las principales conclusiones.

Dependencia espectral de la radiación térmica

Existe una diferencia entre la transferencia de calor por conducción y la transferencia de calor por radiación. La transferencia de calor por radiación se puede filtrar para pasar solo una banda definida de frecuencias de radiación.

En general, se sabe que cuanto más caliente se vuelve un cuerpo, más calor irradia en cada frecuencia.

En una cavidad en un cuerpo opaco con paredes rígidas que no son perfectamente reflectantes a ninguna frecuencia, en equilibrio termodinámico, hay una sola temperatura, y debe ser compartida por la radiación de cada frecuencia.

Uno puede imaginar dos de esas cavidades, cada una en su propio equilibrio radiativo y termodinámico aislado. Uno puede imaginar un dispositivo óptico que permita la transferencia de calor por radiación entre las dos cavidades, filtrado para pasar solo una banda definida de frecuencias de radiación. Si los valores de las radiaciones espectrales de las radiaciones en las cavidades difieren en esa banda de frecuencia, se puede esperar que el calor pase del más caliente al más frío. Se podría proponer utilizar una transferencia de calor filtrada de este tipo en una banda de este tipo para impulsar un motor térmico. Si los dos cuerpos están a la misma temperatura, la segunda ley de la termodinámica no permite que funcione la máquina térmica. Se puede inferir que para una temperatura común a los dos cuerpos, los valores de las radiaciones espectrales en la banda de paso también deben ser comunes. Esto debe ser válido para todas las bandas de frecuencia. Esto quedó claro para Balfour Stewart y más tarde para Kirchhoff. Balfour Stewart encontró experimentalmente que de todas las superficies, una de color negro lámpara emitía la mayor cantidad de radiación térmica para cada calidad de radiación, juzgada por varios filtros.

Pensando teóricamente, Kirchhoff fue un poco más allá y señaló que esto implicaba que la radiación espectral, en función de la frecuencia de radiación, de cualquier cavidad en equilibrio termodinámico debe ser una función universal única de la temperatura. Postuló un cuerpo negro ideal que interactuaba con su entorno de tal manera que absorbía toda la radiación que incide sobre él. Por el principio de reciprocidad de Helmholtz, la radiación del interior de tal cuerpo pasaría sin impedimentos, directamente a sus alrededores sin reflejo en la interfaz. En equilibrio termodinámico, la radiación térmica emitida por tal cuerpo tendría ese resplandor espectral universal único en función de la temperatura. Esta idea es la raíz de la ley de radiación térmica de Kirchhoff.

Relación entre absortividad y emisividad

Uno puede imaginarse un pequeño cuerpo de material esférico homogéneo etiquetado como $X$ a una temperatura $T X$ , que se encuentra en un campo de radiación dentro de una gran cavidad con paredes de material etiquetadas como $Y$ en una temperatura $T Y$ . El cuerpo $X$ emite su propia radiación térmica. En una frecuencia particular $ν$ , la radiación emitida desde una sección transversal particular a través del centro de $X$ en un sentido en una dirección normal a esa sección transversal se puede denotar $I ν, X (T X)$ , característico del material de $X$ . En esa frecuencia $ν$ , la potencia radiativa de las paredes en esa sección transversal en el sentido opuesto en esa dirección se puede denotar $I ν, Y (T Y)$ , para la temperatura de la pared $T Y$ . Para el material de $X$ , definiendo la absortividad $α ν, X, Y (T X, T Y)$ como la fracción de esa radiación incidente absorbida por $X$ , esa energía incidente se absorbe a una tasa $α ν, X, Y (T X, T Y) I ν, Y (T Y)$ .

La tasa $q (ν, T X, T Y)$ de acumulación de energía en un sentido en la sección transversal del cuerpo se puede expresar entonces

{displaystyle q(nuT_{X},T_{Y})=alpha _{nuX,Y}(T_{X},T_{Y})I_{nuY}(T_{Y})-I_{nuX}(T_{X}).}

La idea seminal de Kirchhoff, mencionada anteriormente, fue que, en el equilibrio termodinámico a la temperatura $T$ , existe un único radiativo universal distribución, actualmente denominada $B ν (T)$ , que es independiente de las características químicas de los materiales $X$ y $Y$ , eso conduce a una muy valiosa comprensión del equilibrio de intercambio radiativo de cualquier cuerpo, como sigue.

Cuando hay equilibrio termodinámico a la temperatura $T$ , la radiación de la cavidad de las paredes tiene ese valor universal único, de modo que $I ν, Y (T Y) = B ν (T)$ . Además, se puede definir la emisividad $ε ν, X (T X)$ del material del cuerpo $X$ solo para que en termodinámica equilibrio a la temperatura $T X = T$ , uno tiene <span class="texhtml" I_ν,X(T_X) = I_ν,X(T) = ε_ν,X(T) B_ν(T).

Cuando prevalece el equilibrio térmico a la temperatura $T = T X = T Y$ , la tasa de acumulación de energía se desvanece de modo que $q (ν, T X, T Y) = 0$ . Se sigue que en equilibrio termodinámico, cuando $T = T X = T Y$ ,

{displaystyle 0=alpha _{nuX,Y}(T,T)B_{nu }(T)-epsilon _{nuX}(T)B_{nu }(T).}

Kirchhoff señaló que se sigue que en el equilibrio termodinámico, cuando $T = T X = T Y$ ,

{displaystyle alpha _{nuX,Y}(T,T)=epsilon _{nuX}(T).}

Presentamos la notación especial $α ν, X (T)$ para la absortividad del material $X$ en equilibrio termodinámico a temperatura $T$ (justificado por un descubrimiento de Einstein, como se indica a continuación), se tiene además la igualdad

{displaystyle alpha _{nuX}(T)=epsilon _{nuX}(T)}

La igualdad de absortividad y emisividad aquí demostrada es específica para el equilibrio termodinámico a la temperatura $T$ y, en general, no se espera que se mantenga cuando las condiciones del equilibrio termodinámico no se mantienen. La emisividad y la absortividad son propiedades separadas de las moléculas del material, pero dependen de manera diferente de las distribuciones de los estados de excitación molecular en cada ocasión, debido a un fenómeno conocido como "emisión estimulada", que fue descubierto por Einstein. En ocasiones cuando el material está en equilibrio termodinámico o en un estado conocido como equilibrio termodinámico local, la emisividad y la absortividad se igualan. La radiación incidente muy fuerte u otros factores pueden alterar el equilibrio termodinámico o el equilibrio termodinámico local. El equilibrio termodinámico local en un gas significa que las colisiones moleculares superan con creces la emisión y la absorción de luz al determinar las distribuciones de los estados de excitación molecular.

Kirchhoff señaló que no conocía el carácter preciso de $B ν (T)$ , pero pensó que era importante que se descubriera. Cuatro décadas después de la percepción de Kirchhoff de los principios generales de su existencia y carácter, la contribución de Planck fue determinar la expresión matemática precisa de esa distribución de equilibrio $B ν (T)$ .

Cuerpo negro

En física, se considera un cuerpo negro ideal, denominado aquí $B$ , definido como uno que absorbe por completo toda la radiación electromagnética que cae sobre él. en cada frecuencia $ν$ (de ahí el término "negro"). De acuerdo con la ley de radiación térmica de Kirchhoff, esto implica que, para cada frecuencia $ν$ , en el equilibrio termodinámico a la temperatura $T$ , uno tiene $α ν, B (T) = ε ν, B (T) = 1$ , de modo que la radiación térmica de un cuerpo negro siempre es igual a la cantidad total especificada por la ley de Planck. Ningún cuerpo físico puede emitir una radiación térmica superior a la de un cuerpo negro, ya que si estuviera en equilibrio con un campo de radiación estaría emitiendo más energía de la que incide sobre él.

Aunque no existen materiales perfectamente negros, en la práctica se puede aproximar con precisión una superficie negra. En cuanto a su interior material, un cuerpo de materia condensada, líquida, sólida o de plasma, con una interfaz definida con su entorno, es completamente negro a la radiación si es completamente opaco. Eso significa que absorbe toda la radiación que penetra en la interfaz del cuerpo con su entorno y entra en el cuerpo. Esto no es demasiado difícil de lograr en la práctica. Por otro lado, una interfaz perfectamente negra no se encuentra en la naturaleza. Una interfaz perfectamente negra no refleja radiación, pero transmite todo lo que cae sobre ella, desde cualquier lado. La mejor forma práctica de crear una interfaz negra efectiva es simular una 'interfaz' por un pequeño orificio en la pared de una gran cavidad en un cuerpo rígido de material completamente opaco que no refleja perfectamente en ninguna frecuencia, con sus paredes a temperatura controlada. Más allá de estos requisitos, el material componente de las paredes no tiene restricciones. La radiación que ingresa al orificio casi no tiene posibilidad de escapar de la cavidad sin ser absorbida por múltiples impactos con sus paredes.

La ley del coseno de Lambert

Como explicó Planck, un cuerpo radiante tiene un interior que consta de materia y una interfaz con su medio material vecino contiguo, que suele ser el medio desde el que se observa la radiación de la superficie del cuerpo. La interfase no está compuesta de materia física sino que es una concepción teórica, una superficie bidimensional matemática, una propiedad conjunta de los dos medios contiguos, que estrictamente hablando no pertenecen a ninguno por separado. Tal interfaz no puede absorber ni emitir, porque no está compuesta de materia física; pero es el sitio de reflexión y transmisión de radiación, porque es una superficie de discontinuidad de propiedades ópticas. La reflexión y transmisión de radiación en la interfase obedecen al principio de reciprocidad de Stokes-Helmholtz.

En cualquier punto del interior de un cuerpo negro ubicado dentro de una cavidad en equilibrio termodinámico a temperatura $T$ la radiación es homogénea, isotrópica y no polarizada. Un cuerpo negro absorbe todo y no refleja nada de la radiación electromagnética que incide sobre él. Según el principio de reciprocidad de Helmholtz, la radiación del interior de un cuerpo negro no se refleja en su superficie, sino que se transmite completamente al exterior. Debido a la isotropía de la radiación en el interior del cuerpo, la radiancia espectral de la radiación transmitida desde su interior hacia el exterior a través de su superficie es independiente de la dirección.

Esto se expresa diciendo que la radiación de la superficie de un cuerpo negro en equilibrio termodinámico obedece a la ley del coseno de Lambert. Esto significa que el flujo espectral $d Φ(dA, θ, d Ω, dν)$ de un elemento infinitesimal dado de área $dA$ de la superficie emisora real del negro cuerpo, detectado desde una dirección dada que forma un ángulo $θ$ con la normal a la superficie de emisión real en $dA$ , en un elemento de ángulo sólido de detección $d Ω$ centrado en la dirección indicada por $θ$ , en un elemento del ancho de banda de frecuencia $dν$ , se puede representar como

{displaystyle {frac {dPhi (dA,thetadOmegadnu)}{dOmega }}=L^{0}(dA,dnu),dA,dnu ,cos theta }

L 0 () dA, ♪)

dA

Silencio = 0

El factor $cos θ$ está presente porque el área a la que se refiere directamente la radiación espectral es la proyección, del área de superficie emisora real, sobre un plano perpendicular a la dirección indicada por $θ$ . Esta es la razón del nombre ley del coseno.

Teniendo en cuenta la independencia de la dirección del resplandor espectral de la radiación de la superficie de un cuerpo negro en equilibrio termodinámico, se tiene $L 0 (dA, dν) = B ν (T)$ y así

{displaystyle {frac {dPhi (dA,thetadOmegadnu)}{dOmega }}=B_{nu }(T),dA,dnu ,cos theta.}

Así, la ley del coseno de Lambert expresa la independencia de la dirección de la radiación espectral $B ν (T)$ de la superficie de un cuerpo negro en equilibrio termodinámico.

Ley de Stefan-Boltzmann

La potencia total emitida por unidad de área en la superficie de un cuerpo negro ( $P$ ) se puede encontrar integrando el flujo espectral del cuerpo negro encontrado de la ley de Lambert sobre todas las frecuencias y sobre los ángulos sólidos correspondientes a un hemisferio ( $h$ ) sobre la superficie.

{displaystyle P=int _{0}^{infty }dnu int _{h}dOmega ,B_{nu }cos(theta)}

El ángulo sólido infinitesimal se puede expresar en coordenadas polares esféricas:

{displaystyle dOmega =sin(theta),dtheta ,dphi.}

Para que:

{displaystyle P=int _{0}^{infty }dnu int _{0}^{tfrac {pi }{2}}dtheta int _{0}^{2pi }dphi ,B_{nu }(T)cos(theta)sin(theta)=sigma T^{4}}

{displaystyle sigma ={frac {2k_{mathrm {B} }^{4}pi ^{5}}{15c^{2}h^{3}}}approx 5.670400times 10^{-8},mathrm {J,s^{-1}m^{-2}K^{-4}} }

Transferencia radiativa

La ecuación de transferencia radiativa describe la forma en que la radiación se ve afectada a medida que viaja a través de un medio material. Para el caso especial en el que el medio material se encuentra en equilibrio termodinámico en la vecindad de un punto del medio, la ley de Planck es de especial importancia.

Para simplificar, podemos considerar el estado estacionario lineal, sin dispersión. La ecuación de transferencia radiativa establece que para un haz de luz que atraviesa una pequeña distancia $d s$ , la energía se conserva: El cambio en la (espectral) la radiación de ese rayo ( $I ν$ ) es igual a la cantidad eliminada por el medio material más la cantidad ganada por el medio material. Si el campo de radiación está en equilibrio con el medio material, estas dos contribuciones serán iguales. El medio material tendrá un cierto coeficiente de emisión y coeficiente de absorción.

El coeficiente de absorción $α$ es el cambio fraccionario en la intensidad del haz de luz a medida que recorre la distancia $d s$ , y tiene unidades de longitud⁻¹. Se compone de dos partes, la disminución por absorción y el aumento por emisión estimulada. La emisión estimulada es la emisión del cuerpo material que es causada por la radiación entrante y es proporcional a ella. Se incluye en el término de absorción porque, al igual que la absorción, es proporcional a la intensidad de la radiación entrante. Dado que la cantidad de absorción generalmente variará linealmente con la densidad $ρ$ del material, podemos definir un "coeficiente de absorción de masa" $κ ν = α / ρ$ que es una propiedad del propio material. El cambio de intensidad de un haz de luz debido a la absorción cuando atraviesa una pequeña distancia $d s$ será entonces

{displaystyle dI_{nu }=-kappa _{nu }rho I_{nu },ds}

El "coeficiente de emisión de masa" $j ν$ es igual a la radiancia por unidad de volumen de un elemento de pequeño volumen dividida por su masa (ya que, en cuanto a el coeficiente de absorción de masa, la emisión es proporcional a la masa emisora) y tiene unidades de potencia⋅ángulo sólido⁻¹⋅frecuencia⁻¹⋅densidad⁻¹. Al igual que el coeficiente de absorción de masa, también es una propiedad del propio material. El cambio en un haz de luz cuando atraviesa una pequeña distancia $d s$ será entonces

{displaystyle dI_{nu }=j_{nu }rho ,ds}

La ecuación de transferencia radiativa será entonces la suma de estas dos contribuciones:

{displaystyle {frac {dI_{nu }}{ds}}=j_{nu }rho -kappa _{nu }rho I_{nu }.}

Si el campo de radiación está en equilibrio con el medio material, entonces la radiación será homogénea (independientemente de la posición) de modo que $dI ν = 0$ y:

{displaystyle kappa _{nu }B_{nu }=j_{nu }}

{displaystyle {frac {dI_{nu }}{ds}}=kappa _{nu }rho (B_{nu }-I_{nu }).}

Coeficientes de Einstein

El principio del equilibrio detallado establece que, en el equilibrio termodinámico, cada proceso elemental se equilibra mediante su proceso inverso.

En 1916, Albert Einstein aplicó este principio a nivel atómico al caso de un átomo que irradia y absorbe radiación debido a las transiciones entre dos niveles de energía particulares, lo que brinda una visión más profunda de la ecuación de la transferencia de radiación y la teoría de Kirchhoff. ley para este tipo de radiación. Si el nivel 1 es el nivel de energía inferior con energía $E 1$ , y el nivel 2 es el nivel de energía superior con energía $E 2$ , entonces la frecuencia $ν$ de la radiación radiada o absorbida estará determinada por la condición de frecuencia de Bohr:

{displaystyle E_{2}-E_{1}=hnu.}

Si $n 1$ y $n 2$ son las densidades numéricas del átomo en los estados 1 y 2 respectivamente, entonces la tasa de cambio de estas densidades en el tiempo se deberá a tres procesos:

Emisión espontánea: $left({frac {dn_{1}}{dt}}right)_{mathrm {spon} }=A_{21}n_{2}$
Emisión estimulada: ${displaystyle left({frac {dn_{1}}{dt}}right)_{mathrm {stim} }=B_{21}n_{2}u_{nu }}$
Foto-absorción: ${displaystyle left({frac {dn_{2}}{dt}}right)_{mathrm {abs} }=B_{12}n_{1}u_{nu }}$

donde $u ν$ es la densidad de energía espectral del campo de radiación. Los tres parámetros $A 21$ , $B 21$ y $B 12$ , conocidos como los coeficientes de Einstein, están asociados con el frecuencia de fotones $ν$ producida por la transición entre dos niveles de energía (estados). Como resultado, cada línea de un espectro tiene su propio conjunto de coeficientes asociados. Cuando los átomos y el campo de radiación están en equilibrio, la radiancia vendrá dada por la ley de Planck y, por el principio de equilibrio detallado, la suma de estas tasas debe ser cero:

{displaystyle 0=A_{21}n_{2}+B_{21}n_{2}{frac {4pi }{c}}B_{nu }(T)-B_{12}n_{1}{frac {4pi }{c}}B_{nu }(T)}

Dado que los átomos también están en equilibrio, las poblaciones de los dos niveles están relacionadas por el factor de Boltzmann:

{displaystyle {frac {n_{2}}{n_{1}}}={frac {g_{2}}{g_{1}}}e^{-hnu /k_{mathrm {B} }T}}

g 1

g 2

{displaystyle {frac {A_{21}}{B_{21}}}={frac {8pi hnu ^{3}}{c^{3}}}}

{displaystyle {frac {B_{21}}{B_{12}}}={frac {g_{1}}{g_{2}}}}

j .

κ .

{displaystyle j_{nu }=kappa _{nu }B_{nu }.}

Estos coeficientes se aplican tanto a los átomos como a las moléculas.

Propiedades

Picos

Las distribuciones $B ν$ , $B ω$ , $B ν̃$ y $Pico de B k$ a una energía fotónica de

{displaystyle E=left[3+Wleft(-3e^{-3}right)right]k_{mathrm {B} }Tapprox 2.821 k_{mathrm {B} }T,}

W

e

Sin embargo, la distribución $B λ$ alcanza su punto máximo a una energía diferente

{displaystyle E=left[5+Wleft(-5e^{-5}right)right]k_{mathrm {B} }Tapprox 4.965 k_{mathrm {B} }T,}

B .

B λ

.

λ

{textstyle left|{dnu }/{dlambda }right|=c/{lambda ^{2}}}

modo

hc

14387.770 μm·K

La radiación espectral en estos picos viene dada por:

{displaystyle {begin{aligned}B_{nu{text{max}}}(T)&={frac {2k_{mathrm {B} }^{3}T^{3}x^{3}}{h^{2}c^{2}}}{frac {1}{e^{x}-1}}\&approx 1.896times 10^{-19}{frac {mathrm {W} }{mathrm {m^{2}cdot Hzcdot sr} }}times (T/mathrm {K})^{3}\end{aligned}}}

con ${displaystyle x=3+W(-3e^{-3}),}$ y

{displaystyle {begin{aligned}B_{lambda{text{max}}}(T)&={frac {2k_{mathrm {B} }^{5}T^{5}x^{5}}{h^{4}c^{3}}}{frac {1}{e^{x}-1}}\&approx 4.096times 10^{-6}{frac {text{W}}{{text{m}}^{2}cdot {text{sr}}}}times ~(T/{text{K}})^{5}end{aligned}}}

{displaystyle x=5+W(-5e^{-5}).}

Mientras tanto, la energía promedio de un fotón de un cuerpo negro es

{displaystyle E=left[{frac {pi ^{4}}{30 zeta (3)}}right]k_{mathrm {B} }Tapprox 2.701 k_{mathrm {B} }T,}

zeta

Aproximaciones

Parcelas de radiancia vs. frecuencia para la ley de Planck (verde), en comparación con la ley Rayleigh-Jeans (rojo) y la aproximación de Wien (azul) para un cuerpo negro a 8 mK de temperatura.

En el límite de bajas frecuencias (es decir, longitudes de onda largas), la ley de Planck se convierte en la ley de Rayleigh-Jeans

{displaystyle B_{nu }(T)approx {frac {2nu ^{2}}{c^{2}}}k_{mathrm {B} }T}

{displaystyle B_{lambda }(T)approx {frac {2c}{lambda ^{4}}}k_{mathrm {B} }T}

El resplandor aumenta con el cuadrado de la frecuencia, lo que ilustra la catástrofe ultravioleta. En el límite de las altas frecuencias (es decir, longitudes de onda pequeñas), la ley de Planck tiende a la aproximación de Wien:

{displaystyle B_{nu }(T)approx {frac {2hnu ^{3}}{c^{2}}}e^{-{frac {hnu }{k_{mathrm {B} }T}}}}

{displaystyle B_{lambda }(T)approx {frac {2hc^{2}}{lambda ^{5}}}e^{-{frac {hc}{lambda k_{mathrm {B} }T}}}.}

Percentiles

Percentil	$λ T$ (μm·K)	$λ k B T / hc$
0,01%	910	0,0632
0,1%	1110	0,0771
1%	1448	0.1006
10%	2195	0.1526
20%	2676	0.1860
25.0%	2898	0.2014
30%	3119	0.2168
40%	3582	0,2490
41.8%	3670	0,251
50%	4107	0,255
60%	4745	0,3298
64,6%	5099	0,3544
70%	5590	0,3885
80%	6864	0.4771
90%	9376	0,6517
99%	22884	1.5905
99,9%	51613	3.5873
99,99%	113374	7.8799

La ley de desplazamiento de Wien en su forma más fuerte establece que la forma de la ley de Planck es independiente de la temperatura. Por lo tanto, es posible enumerar los puntos percentiles de la radiación total, así como los picos de longitud de onda y frecuencia, en una forma que da la longitud de onda $λ$ cuando se divide por la temperatura $T$ . La segunda columna de la siguiente tabla enumera los valores correspondientes de $λT$ , es decir, los valores de $x$ para la cual la longitud de onda $λ$ es $x / T$ micrómetros en el punto percentil de radiancia dado por la entrada correspondiente en la primera columna.

Es decir, el 0,01 % de la radiación se encuentra en una longitud de onda inferior a $910 / T$ µm, 20 % por debajo de $2676 / T µm$ , etc. Los picos de longitud de onda y frecuencia están en negrita y ocurren al 25,0 % y al 64,6 % respectivamente. El punto del 41,8 % es el pico neutral de longitud de onda y frecuencia (es decir, el pico de potencia por unidad de cambio en el logaritmo de longitud de onda o frecuencia). Estos son los puntos en los que las respectivas funciones de la ley de Planck $1 / λ 5$ , $ν 3$ y $ν 2 / λ 2$ , respectivamente, dividido por $exp (hν / k B T) - 1$ alcanzan sus máximos. La brecha mucho menor en la proporción de longitudes de onda entre 0,1% y 0,01% (1110 es 22% más que 910) que entre 99,9% y 99,99% (113374 es 120% más que 51613) refleja la disminución exponencial de la energía en longitudes de onda cortas (izquierda end) y el decaimiento polinomial en long.

Qué pico usar depende de la aplicación. La elección convencional es el pico de longitud de onda al 25,0 % dado por la ley de desplazamiento de Wien en su forma débil. Para algunos propósitos, la mediana o el punto del 50% que divide la radiación total en dos mitades puede ser más adecuado. Este último está más cerca del pico de frecuencia que del pico de longitud de onda porque la radiancia cae exponencialmente en longitudes de onda cortas y solo polinomialmente en longitudes de onda largas. El pico neutral ocurre en una longitud de onda más corta que la mediana por la misma razón.

espectro solar comparado con cuerpo negro a 5775 K

Percentil	Sol $λ$ (μm)	Cuerpo negro en 5778K	288 K planeta $λ$ (μm)
0,01%	0.203	0.157	3.16
0,1%	0,235	0.192	3.85
1%	0.296	0.251	5.03
10%	0.415	0,380	7.62
20%	0.484	0.463	9.29
25.0%	0,520	0.502	10.1
30%	0,565	.540	10.8
41.8%	0.650	0,635	12.7
50%	0,2727	0.711	14.3
60%	0.844	0.821	16,5
64,6%	0.911	0.882	17,7
70%	1.003	0.967	19.4
80%	1.242	1.188	23.8
90%	1.666	1.623	32.6
99%	3.728	3.961	79,5
99,9%	8.208	8.933	179
99,99%	17.548	19.620	394

Comparación con el espectro solar

La radiación solar se puede comparar con la radiación del cuerpo negro a aproximadamente 5778 K (pero vea el gráfico). La tabla de la derecha muestra cómo se reparte la radiación de un cuerpo negro a esta temperatura, y también cómo se reparte la luz solar a modo de comparación. También a modo de comparación, se muestra un planeta modelado como un cuerpo negro, que irradia a 288 K nominales (15 °C) como valor representativo de la temperatura altamente variable de la Tierra. Sus longitudes de onda son más de veinte veces las del Sol, tabuladas en la tercera columna en micrómetros (miles de nanómetros).

Es decir, solo el 1 % de la radiación solar se encuentra en longitudes de onda inferiores a 296 nm y solo el 1 % en longitudes de onda superiores a 3728 nm. Expresado en micrómetros, esto sitúa al 98 % de la radiación solar en el rango de 0,296 a 3,728 µm. El 98 % correspondiente de la energía radiada por un planeta de 288 K es de 5,03 a 79,5 µm, muy por encima del rango de radiación solar (o por debajo si se expresa en términos de frecuencias $ν = c / λ$ en lugar de longitudes de onda $λ).$

Una consecuencia de esta diferencia de más del orden de magnitud en la longitud de onda entre la radiación solar y la planetaria es que los filtros diseñados para pasar una y bloquear la otra son fáciles de construir. Por ejemplo, las ventanas fabricadas con vidrio ordinario o plástico transparente dejan pasar al menos el 80 % de la radiación solar entrante de 5778 K, que tiene una longitud de onda inferior a 1,2 µm, mientras que bloquean más del 99 % de la radiación térmica saliente de 288 K a partir de 5 µm, longitudes de onda en el que la mayoría de los tipos de vidrio y plástico de espesor de grado de construcción son efectivamente opacos.

La radiación del Sol es la que llega a la parte superior de la atmósfera (TOA). Como se puede leer en la tabla, la radiación por debajo de 400 nm, o ultravioleta, es aproximadamente el 8 %, mientras que la radiación por encima de 700 nm, o infrarroja, comienza aproximadamente en el punto del 48 % y, por lo tanto, representa el 52 % del total. Por lo tanto, solo el 40% de la insolación TOA es visible para el ojo humano. La atmósfera cambia sustancialmente estos porcentajes a favor de la luz visible, ya que absorbe la mayor parte de los rayos ultravioleta y cantidades significativas de infrarrojos.

Derivación

Considere un cubo de lado $L$ con paredes conductoras llenas de radiación electromagnética en equilibrio térmico a la temperatura $T$ . Si hay un pequeño agujero en una de las paredes, la radiación emitida por el agujero será característica de un cuerpo negro perfecto. Primero calcularemos la densidad de energía espectral dentro de la cavidad y luego determinaremos la radiancia espectral de la radiación emitida.

En las paredes del cubo, la componente paralela del campo eléctrico y la componente ortogonal del campo magnético deben desaparecer. De forma análoga a la función de onda de una partícula en una caja, se encuentra que los campos son superposiciones de funciones periódicas. Las tres longitudes de onda $λ 1$ , $λ 2$ , y $λ 3$ , en las tres direcciones ortogonales a las paredes pueden ser:

{displaystyle lambda _{i}={frac {2L}{n_{i}}},}

n i

n i

n i

{displaystyle E_{n_{1},n_{2},n_{3}}left(rright)=left(r+{frac {1}{2}}right){frac {hc}{2L}}{sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}

()1)

El número $r$ se puede interpretar como el número de fotones en el modo. Para $r = 0$ la energía del modo no es cero. Esta energía de vacío del campo electromagnético es responsable del efecto Casimir. A continuación calcularemos la energía interna de la caja a la temperatura absoluta $T$ .

Según la mecánica estadística, la distribución de probabilidad de equilibrio sobre los niveles de energía de un modo en particular viene dada por:

{displaystyle P_{r}={frac {e^{-beta Eleft(rright)}}{Zleft(beta right)}}.}

{displaystyle beta {stackrel {mathrm {def} }{=}} {frac {1}{k_{mathrm {B} }T}}.}

Z () β)

P r

{displaystyle Zleft(beta right)=sum _{r=0}^{infty }e^{-beta Eleft(rright)}={frac {e^{-beta varepsilon /2}}{1-e^{-beta varepsilon }}},}

{displaystyle varepsilon ={frac {hc}{2L}}{sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}

()2)

siendo la energía de un solo fotón. La energía promedio en un modo se puede obtener de la función de partición:

{displaystyle leftlangle Erightrangle =-{frac {dlog left(Zright)}{dbeta }}={frac {varepsilon }{2}}+{frac {varepsilon }{e^{beta varepsilon }-1}}.}

Si medimos la energía en relación con el estado fundamental, la energía total en el cuadro sigue al sumar $⟨ E ⟩ - ε / 2$ sobre todos los estados de fotón único permitidos. Esto se puede hacer exactamente en el límite termodinámico cuando $L$ se acerca al infinito. En este límite, $ε$ se vuelve continuo y podemos integrar $⟨ E ⟩ - ε / 2$ sobre este parámetro. Para calcular la energía en la caja de esta manera, necesitamos evaluar cuántos estados de fotones hay en un rango de energía dado. Si escribimos el número total de estados de un solo fotón con energías entre $ε$ y $ε + dε$ como $g (ε) dε$ , donde $g (ε)$ es la densidad de estados (que se evalúa a continuación), luego la energía total es dado por

{displaystyle U=int _{0}^{infty }{frac {varepsilon }{e^{beta varepsilon }-1}}g(varepsilon),dvarepsilon.}

()3)

Para calcular la densidad de estados reescribimos la ecuación (2) de la siguiente manera:

{displaystyle varepsilon {=} {frac {hc}{2L}}n,}

n

n = n 1, n 2, n 3)

Para cada vector $n$ con componentes enteros mayores o iguales a cero, hay dos estados de fotones. Esto significa que el número de estados de fotones en una cierta región del $n$ -espacio es el doble del volumen de esa región. Un rango de energía de $dε$ corresponde a una capa de espesor $dn = 2 L / hc d ε$ en $n$ -espacio. Debido a que los componentes de $n$ tienen que ser positivos, este caparazón abarca un octante de una esfera. El número de estados de fotones $g (ε) dε$ , en un rango de energía $dε$ , viene dada por:

{displaystyle g(varepsilon),dvarepsilon =2{frac {1}{8}}4pi n^{2},dn={frac {8pi L^{3}}{h^{3}c^{3}}}varepsilon ^{2},dvarepsilon.}

V = L 3

{displaystyle {frac {U}{V}}=int _{0}^{infty }u_{nu }(T),dnu}

u . () T)

{displaystyle u_{nu }(T)={8pi hnu ^{3} over c^{3}}{1 over e^{hnu /k_{mathrm {B} }T}-1}.}

{displaystyle B_{nu }(T)={frac {u_{nu }(T)c}{4pi }},}

{displaystyle B_{nu }(T)={frac {2hnu ^{3}}{c^{2}}}~{frac {1}{e^{hnu /k_{mathrm {B} }T}-1}}.}

Historia

Balfour Estuardo

En 1858, Balfour Stewart describió sus experimentos sobre los poderes emisivos y absorbentes de radiación térmica de placas pulidas de diversas sustancias, en comparación con los poderes de superficies de color negro lámpara, a la misma temperatura. Stewart eligió las superficies de color negro lámpara como referencia debido a varios hallazgos experimentales previos, especialmente los de Pierre Prevost y John Leslie. Escribió: "La lámpara negra, que absorbe todos los rayos que caen sobre ella y, por lo tanto, posee el mayor poder de absorción posible, poseerá también el mayor poder de radiación posible".

Stewart midió la potencia radiada con una termopila y un galvanómetro sensible leyó con un microscopio. Estaba preocupado por la radiación térmica selectiva, que investigó con placas de sustancias que irradiaban y absorbían selectivamente para diferentes calidades de radiación en lugar de máximamente para todas las calidades de radiación. Discutió los experimentos en términos de rayos que podían reflejarse y refractarse, y que obedecían el principio de reciprocidad de Helmholtz (aunque no usó un epónimo para ello). En este artículo no mencionó que las cualidades de los rayos podrían describirse por sus longitudes de onda, ni utilizó aparatos de resolución espectral como prismas o rejillas de difracción. Su trabajo fue cuantitativo dentro de estas limitaciones. Hizo sus mediciones en un ambiente a temperatura ambiente, y rápidamente para atrapar sus cuerpos en una condición cercana al equilibrio térmico en el que habían sido preparados calentándolos hasta el equilibrio con agua hirviendo. Sus mediciones confirmaron que las sustancias que emiten y absorben selectivamente respetan el principio de igualdad selectiva de emisión y absorción en equilibrio térmico.

Stewart ofreció una prueba teórica de que este debería ser el caso por separado para cada cualidad seleccionada de radiación térmica, pero sus matemáticas no eran rigurosamente válidas. Según el historiador D. M. Siegel: 'Él no practicaba las técnicas más sofisticadas de la física matemática del siglo XIX; ni siquiera hizo uso de la notación funcional al tratar con distribuciones espectrales." No mencionó la termodinámica en este artículo, aunque sí se refirió a la conservación de vis viva. Propuso que sus medidas implicaban que la radiación era tanto absorbida como emitida por partículas de materia a lo largo de las profundidades de los medios en los que se propagaba. Aplicó el principio de reciprocidad de Helmholtz para dar cuenta de los procesos de interfaz material a diferencia de los procesos en el material interior. Concluyó que sus experimentos mostraban que, en el interior de un recinto en equilibrio térmico, el calor radiante, reflejado y emitido combinado, que dejaba cualquier parte de la superficie, independientemente de su sustancia, era el mismo que habría dejado esa misma porción de la superficie si hubiera estado compuesta de negro de humo. No mencionó la posibilidad de paredes idealmente perfectamente reflectantes; en particular, notó que los metales físicos reales altamente pulidos absorben muy poco.

Gustav Kirchhoff

En 1859, sin conocer el trabajo de Stewart, Gustav Robert Kirchhoff informó de la coincidencia de las longitudes de onda de las líneas de absorción y emisión de luz visible resueltas espectralmente. De manera importante para la física térmica, también observó que las líneas brillantes u oscuras eran aparentes dependiendo de la diferencia de temperatura entre el emisor y el absorbente.

Kirchhoff luego pasó a considerar los cuerpos que emiten y absorben radiación de calor, en un recinto o cavidad opaca, en equilibrio a la temperatura $T$ .

Aquí se utiliza una notación diferente a la de Kirchhoff. Aquí, la potencia de emisión $E (T, i)$ denota una cantidad dimensionada, la radiación total emitida por un cuerpo etiquetado por el índice $i$ a la temperatura $T$ . La relación de absorción total $a (T, i)$ de ese cuerpo es adimensional, el relación entre la radiación absorbida y la incidente en la cavidad a la temperatura $T$ . (En contraste con la definición de Balfour Stewart, la definición de Kirchhoff de su relación de absorción no se refería en particular a una superficie negra como la fuente de la radiación incidente). Por lo tanto, la relación $E (T, i) / a (T, i)$ de la potencia de emisión a la relación de absorción es una cantidad dimensionada, con las dimensiones de la potencia de emisión, porque $a (T, i)$ es adimensional. También aquí, el poder de emisión específico de la longitud de onda del cuerpo a la temperatura $T$ se denota por $E (λ, T, i)$ y la relación de absorción específica de la longitud de onda por $a (λ, T, i)$ . De nuevo, la relación $E (λ, T, i) / a (λ, T, i)$ de potencia de emisión a absorción La relación es una cantidad dimensionada, con las dimensiones de la potencia de emisión.

En un segundo informe realizado en 1859, Kirchhoff anunció un nuevo principio general o ley para el cual ofreció una prueba teórica y matemática, aunque no ofreció medidas cuantitativas de los poderes de radiación. Su prueba teórica fue y sigue siendo considerada por algunos escritores como inválida. Su principio, sin embargo, ha perdurado: era que para los rayos de calor de la misma longitud de onda, en equilibrio a una temperatura dada, la relación específica de longitud de onda entre la potencia de emisión y la relación de absorción tiene el mismo valor común para todos los cuerpos que emiten y absorber a esa longitud de onda. En símbolos, la ley establece que la proporción específica de longitud de onda $E (λ, T, i) / a (λ, T, i)$ tiene el mismo valor para todos los cuerpos, es decir, para todos los valores del índice $i$ . En este informe no se mencionan los cuerpos negros.

En 1860, sin conocer aún las medidas de Stewart para determinadas calidades de radiación, Kirchhoff señaló que se había establecido experimentalmente durante mucho tiempo que para la radiación de calor total, de calidad no seleccionada, emitida y absorbida por un cuerpo en equilibrio, la relación de radiación total dimensionada $E (T, i) / a (T, i)$ , tiene un mismo valor común a todos los cuerpos, es decir, para cada valor del índice material $i$ . Nuevamente sin mediciones de potencias radiativas u otros nuevos datos experimentales, Kirchhoff ofreció una nueva prueba teórica de su nuevo principio de la universalidad del valor de la relación específica de longitud de onda $E (λ, T, i) / a (λ, T, i)$ en equilibrio térmico. Su nueva prueba teórica fue y sigue siendo considerada por algunos escritores como inválida.

Pero, lo que es más importante, se basó en un nuevo postulado teórico de "cuerpos perfectamente negros", razón por la cual se habla de la ley de Kirchhoff. Tales cuerpos negros mostraban una absorción completa en su superficie más superficial, infinitamente delgada. Corresponden a los cuerpos de referencia de Balfour Stewart, con radiación interna, recubiertos con negro de humo. No eran los cuerpos perfectamente negros más realistas considerados más tarde por Planck. Los cuerpos negros de Planck irradiados y absorbidos únicamente por el material de sus interiores; sus interfaces con medios contiguos eran solo superficies matemáticas, capaces de no absorber ni emitir, sino solo de reflejar y transmitir con refracción.

La prueba de Kirchhoff consideró un cuerpo no ideal arbitrario etiquetado como $i$ así como varios cuerpos negros perfectos etiquetados como BB. Requería que los cuerpos se mantuvieran en una cavidad en equilibrio térmico a temperatura $T$ . Su prueba pretendía mostrar que la razón $E (λ, T, i) / a (λ, T, i)$ fue independiente de la naturaleza $i$ del cuerpo no ideal, por muy parcialmente transparente o parcialmente reflexivo que fuera.

Su prueba argumentó primero que para la longitud de onda $λ$ y a la temperatura $T$ , en equilibrio térmico, todos los cuerpos perfectamente negros del mismo tamaño y forma tienen el mismo valor común de poder emisivo $E (λ, T, BB)$ , con las dimensiones del poder. Su prueba señaló que la relación de absorción específica de la longitud de onda adimensional $a (λ, T, BB)$ de un cuerpo perfectamente negro es, por definición, exactamente 1. Entonces, para un cuerpo perfectamente negro, la relación específica de longitud de onda entre la potencia de emisión y la relación de absorción $E (λ, T, BB) / a (λ, T, BB)$ es nuevamente $E (λ, T, BB)$ , con las dimensiones del poder. Kirchhoff consideró, sucesivamente, el equilibrio térmico con el cuerpo arbitrario no ideal, y con un cuerpo perfectamente negro del mismo tamaño y forma, colocado en su cavidad en equilibrio a la temperatura $T$ . Argumentó que los flujos de radiación de calor deben ser los mismos en cada caso. Por lo tanto, argumentó que en el equilibrio térmico la relación $E (λ, T, i) / a (λ, T, i)$ era igual a $E (λ, T, BB)$ , que ahora se puede denotar $B λ (λ, T)$ , una función continua, que depende solo de $λ$ a temperatura fija $T$ , y una función creciente de $T$ a una longitud de onda fija $λ$ , a bajas temperaturas, desvaneciéndose para longitudes de onda visibles pero no para longitudes de onda más largas, con valores positivos para longitudes de onda visibles a temperaturas más altas, lo que no depende de la naturaleza $i$ del cuerpo arbitrario no ideal. (Los factores geométricos, tenidos en cuenta detalladamente por Kirchhoff, han sido ignorados en lo anterior.)

Por lo tanto, la ley de radiación térmica de Kirchhoff puede establecerse: Para cualquier material, radiando y absorbiendo en equilibrio termodinámico a cualquier temperatura dada $T$ , para cada longitud de onda $λ$ , la relación entre el poder de emisión y la relación de absorción tiene un valor universal, que es característico de un cuerpo negro perfecto, y es un poder de emisión que aquí representamos por $B λ (λ, T)$ . (Para nuestra notación $B λ (λ, T)$ , la notación original de Kirchhoff era simplemente $e$ ).

Kirchhoff anunció que la determinación de la función $B λ (λ, T)$ era un problema de la mayor importancia, aunque reconoció que habría dificultades experimentales que superar. Supuso que, como otras funciones que no dependen de las propiedades de los cuerpos individuales, sería una función simple. Esa función $B λ (λ, T)$ ha sido llamada ocasionalmente "función (de emisión, universal) de Kirchhoff", aunque su forma matemática precisa no se conocería hasta otros cuarenta años, hasta que fue descubierta por Planck en 1900. La prueba teórica del principio de universalidad de Kirchhoff fue elaborada y debatida por varios físicos al mismo tiempo y más tarde. Kirchhoff afirmó más tarde en 1860 que su demostración teórica era mejor que la de Balfour Stewart, y en algunos aspectos lo era. El artículo de Kirchhoff de 1860 no mencionaba la segunda ley de la termodinámica y, por supuesto, no mencionaba el concepto de entropía, que no se había establecido en ese momento. En un relato más considerado en un libro de 1862, Kirchhoff mencionó la conexión de su ley con el 'principio de Carnot', que es una forma de la segunda ley.

Según Helge Kragh, "la teoría cuántica debe su origen al estudio de la radiación térmica, en particular al "cuerpo negro" radiación que Robert Kirchhoff había definido por primera vez en 1859-1860."

Ingredientes empíricos y teóricos para la inducción científica de la ley de Planck

En 1860, Kirchhoff predijo dificultades experimentales para la determinación empírica de la función que describía la dependencia del espectro del cuerpo negro en función únicamente de la temperatura y la longitud de onda. Y así resultó. Fueron necesarios unos cuarenta años de desarrollo de métodos mejorados de medición de la radiación electromagnética para obtener un resultado fiable.

En 1865, John Tyndall describió la radiación de los filamentos calentados eléctricamente y de los arcos de carbono como visible e invisible. Tyndall descompuso espectralmente la radiación mediante el uso de un prisma de sal de roca, que transmitía calor y rayos visibles, y midió la intensidad de la radiación mediante una termopila.

En 1880, André-Prosper-Paul Crova publicó un diagrama de la apariencia tridimensional del gráfico de la fuerza de la radiación térmica en función de la longitud de onda y la temperatura. Determinó la variable espectral mediante el uso de prismas. Analizó la superficie a través de lo que llamó "isotérmico" curvas, secciones para una sola temperatura, con una variable espectral en las abscisas y una variable de potencia en las ordenadas. Puso curvas suaves a través de sus puntos de datos experimentales. Tenían un pico en un valor espectral característico de la temperatura y caían a ambos lados del mismo hacia el eje horizontal. Tales secciones espectrales se muestran ampliamente incluso hoy en día.

En una serie de artículos de 1881 a 1886, Langley informó sobre mediciones del espectro de radiación de calor, utilizando rejillas y prismas de difracción, y los detectores más sensibles que pudo fabricar. Informó que había un pico de intensidad que aumentaba con la temperatura, que la forma del espectro no era simétrica con respecto al pico, que había una fuerte disminución de la intensidad cuando la longitud de onda era más corta que un valor de corte aproximado para cada temperatura, que la longitud de onda de corte aproximada disminuyó con el aumento de la temperatura, y que la longitud de onda de la intensidad máxima disminuyó con la temperatura, de modo que la intensidad aumentó fuertemente con la temperatura para longitudes de onda cortas que eran más largas que el corte aproximado para la temperatura.

Después de haber leído a Langley, en 1888, el físico ruso V.A. Michelson publicó una consideración de la idea de que la función de radiación de Kirchhoff desconocida podría explicarse físicamente y expresarse matemáticamente en términos de "irregularidad completa de las vibraciones de... los átomos". En ese momento, Planck no estaba estudiando la radiación de cerca y no creía ni en los átomos ni en la física estadística. Michelson produjo una fórmula para el espectro de temperatura:

{displaystyle I_{lambda }=B_{1}theta ^{frac {3}{2}}exp left(-{frac {c}{lambda ^{2}theta }}right)lambda ^{-6},}

I λ

λ

Silencio

B 1

c

En 1898, Otto Lummer y Ferdinand Kurlbaum publicaron un relato de su fuente de radiación de cavidad. Su diseño se ha utilizado prácticamente sin cambios para las mediciones de radiación hasta el día de hoy. Era una caja de platino, dividida por diafragmas, con su interior ennegrecido con óxido de hierro. Fue un ingrediente importante para las mediciones progresivamente mejoradas que llevaron al descubrimiento de la ley de Planck. Una versión descrita en 1901 tenía el interior ennegrecido con una mezcla de óxidos de cromo, níquel y cobalto.

La importancia de la fuente de radiación de la cavidad de Lummer y Kurlbaum radicaba en que era una fuente experimentalmente accesible de radiación de cuerpo negro, a diferencia de la radiación de un cuerpo sólido incandescente simplemente expuesto, que había sido la aproximación experimental más cercana disponible a la radiación de cuerpo negro. radiación corporal en un rango adecuado de temperaturas. Los cuerpos sólidos incandescentes simplemente expuestos, que se habían utilizado antes, emitían radiación con desviaciones del espectro del cuerpo negro que hacía imposible encontrar el verdadero espectro del cuerpo negro a partir de los experimentos.

Las opiniones de Planck ante los hechos empíricos lo llevaron a encontrar su eventual ley

Planck centró su atención por primera vez en el problema de la radiación del cuerpo negro en 1897. El progreso teórico y empírico permitió a Lummer y Pringsheim escribir en 1899 que la evidencia experimental disponible era aproximadamente consistente con la ley de intensidad específica $Cλ -5 e - c ⁄ λT$ donde $C$ y $c$ indican constantes medibles empíricamente, y donde $λ$ y $T$ denota longitud de onda y temperatura respectivamente. Por razones teóricas, Planck en ese momento aceptó esta formulación, que tiene un corte efectivo de longitudes de onda cortas.

Gustav Kirchhoff fue el maestro de Max Planck y supuso que había una ley universal para la radiación del cuerpo negro y esto se llamó 'el desafío de Kirchhoff'. Planck, un teórico, creía que Wilhelm Wien había descubierto esta ley y Planck amplió el trabajo de Wien presentándolo en 1899 en la reunión de la Sociedad Alemana de Física. Los experimentalistas Otto Lummer, Ferdinand Kurlbaum, Ernst Pringsheim Sr. y Heinrich Rubens realizaron experimentos que parecían respaldar la ley de Wien, especialmente en longitudes de onda cortas de frecuencia más alta, que Planck respaldó tan completamente en la Sociedad Alemana de Física que comenzó a llamarse el Ley de Wien-Planck. Sin embargo, en septiembre de 1900, los experimentadores habían demostrado sin lugar a dudas que la ley de Wien-Planck fallaba en las longitudes de onda más largas. Presentarían sus datos el 19 de octubre. Planck fue informado por su amigo Rubens y rápidamente creó una fórmula en pocos días. En junio de ese mismo año, Lord Raleigh había creado una fórmula que funcionaría para longitudes de onda cortas de baja frecuencia basada en la teoría ampliamente aceptada de equipartición. Así que Planck presentó una fórmula que combinaba la ley de Raleigh (o una teoría de equipartición similar) y la ley de Wien, que se ponderaría según una u otra ley según la longitud de onda para que coincida con los datos experimentales. Sin embargo, aunque esta ecuación funcionó, el propio Planck dijo que a menos que pudiera explicar la fórmula derivada de una "intuición afortunada" en uno de "verdadero significado" en física, no tenía un verdadero significado. Planck explicó que a partir de entonces siguió el trabajo más duro de su vida. Planck no creía en los átomos, ni pensaba que la segunda ley de la termodinámica debería ser estadística porque la probabilidad no proporciona una respuesta absoluta, y la ley de la entropía de Boltzmann se basaba en la hipótesis de los átomos y era estadística. Pero Planck no pudo encontrar una manera de reconciliar su ecuación de Blackbody con leyes continuas como las ecuaciones de onda de Maxwell. Entonces, en lo que Planck llamó 'un acto de desesperación', recurrió a la ley atómica de la entropía de Boltzmann, ya que era la única que hacía que su ecuación funcionara. Por lo tanto, usó la constante de Boltzmann k y su nueva constante h para explicar la ley de radiación del cuerpo negro que se hizo ampliamente conocida a través de su artículo publicado.

Encontrar la ley empírica

Max Planck elaboró su ley el 19 de octubre de 1900 como una mejora de la aproximación de Wien, publicada en 1896 por Wilhelm Wien, que se ajustaba a los datos experimentales en longitudes de onda cortas (altas frecuencias) pero se desviaba de ellos en longitudes de onda largas (bajas frecuencias). En junio de 1900, basado en consideraciones teóricas heurísticas, Rayleigh había sugerido una fórmula que proponía podría comprobarse experimentalmente. La sugerencia fue que la función universal de Stewart-Kirchhoff podría tener la forma $c 1 Tλ -4 exp(- c 2 / λT)$ . Esta no era la célebre fórmula de Rayleigh-Jeans $8π k B Tλ -4$ , que no surgió hasta 1905, aunque se redujo a este último para longitudes de onda largas, que son las relevantes aquí. Según Klein, se puede especular que es probable que Planck haya visto esta sugerencia, aunque no la mencionó en sus artículos de 1900 y 1901. Planck habría estado al tanto de varias otras fórmulas propuestas que se habían ofrecido. El 7 de octubre de 1900, Rubens le dijo a Planck que en el dominio complementario (longitud de onda larga, baja frecuencia), y solo allí, la fórmula de Rayleigh de 1900 se ajustaba bien a los datos observados.

Para longitudes de onda largas, la fórmula heurística de Rayleigh de 1900 significaba aproximadamente que la energía era proporcional a la temperatura, $U λ = const. T$ . Se sabe que $dS / dU λ = 1 / T$ y esto conduce a $dS / dU λ = const. / U λ$ y de allí a $d 2 S / dU λ 2 = - const. / U λ 2$ para longitudes de onda largas. Pero para longitudes de onda cortas, la fórmula de Wien conduce a $1 / T = - const. ln U λ + const.$ y de allí a $d 2 S / dU λ 2$ = − const./U_λ para longitudes de onda cortas. Planck quizás unió estas dos fórmulas heurísticas, para longitudes de onda largas y cortas, para producir una fórmula

{displaystyle {frac {d^{2}S}{dU_{lambda }^{2}}}={frac {alpha }{U_{lambda }(beta +U_{lambda })}}.}

Esto llevó a Planck a la fórmula

{displaystyle B_{lambda }(T)={frac {Clambda ^{-5}}{e^{frac {c}{lambda T}}-1}},}

C

c

Planck envió este resultado a Rubens, quien lo comparó con sus datos de observación y los de Kurlbaum y descubrió que se ajustaba notablemente bien a todas las longitudes de onda. El 19 de octubre de 1900, Rubens y Kurlbaum informaron brevemente sobre el ajuste de los datos y Planck agregó una breve presentación para dar un bosquejo teórico que explicara su fórmula. En una semana, Rubens y Kurlbaum dieron un informe más completo de sus medidas que confirmaban la ley de Planck. Su técnica para la resolución espectral de la radiación de longitud de onda más larga se denominó método de rayos residuales. Los rayos se reflejaron repetidamente desde las superficies de cristal pulido, y los rayos que atravesaron todo el proceso fueron 'residuales' y tenían longitudes de onda reflejadas preferentemente por cristales de materiales adecuadamente específicos.

Tratando de encontrar una explicación física de la ley

Una vez que Planck descubrió la función de ajuste empírico, construyó una derivación física de esta ley. Su pensamiento giraba en torno a la entropía en lugar de centrarse directamente en la temperatura. Planck consideró una cavidad con paredes perfectamente reflectantes; dentro de la cavidad, hay un número finito de cuerpos oscilatorios resonantes de magnitud definida, distintos pero constituidos de forma idéntica, con varios osciladores de este tipo en cada una de las frecuencias características finitas. Estos osciladores hipotéticos fueron para Planck sondas de investigación teóricas puramente imaginarias, y dijo de ellos que tales osciladores no necesitan "realmente existir en algún lugar de la naturaleza, siempre que su existencia y sus propiedades sean consistentes con las leyes de la termodinámica y la electrodinámica". ". Planck no atribuyó ningún significado físico definitivo a su hipótesis de los osciladores resonantes, sino que la propuso como un dispositivo matemático que le permitía derivar una única expresión para el espectro del cuerpo negro que coincidía con los datos empíricos en todas las longitudes de onda. Mencionó tentativamente la posible conexión de tales osciladores con átomos. En cierto sentido, los osciladores correspondían a la mota de carbono de Planck; el tamaño de la mota podría ser pequeño independientemente del tamaño de la cavidad, siempre que la mota transdujese energía de manera efectiva entre los modos de longitud de onda radiativa.

Siguiendo en parte un método heurístico de cálculo iniciado por Boltzmann para las moléculas de gas, Planck consideró las posibles formas de distribuir la energía electromagnética entre los diferentes modos de sus hipotéticos osciladores de material cargado. Esta aceptación del enfoque probabilístico, siguiendo a Boltzmann, supuso para Planck un cambio radical con respecto a su posición anterior, que hasta entonces se había opuesto deliberadamente al pensamiento propuesto por Boltzmann. En palabras de Planck, "consideré la [hipótesis cuántica] como una suposición puramente formal, y no le di mucha importancia excepto por esto: que había obtenido un resultado positivo bajo cualquier circunstancia y a cualquier costo".." Heurísticamente, Boltzmann había distribuido la energía en cuantos meramente matemáticos arbitrarios $ϵ$ , que había procedido a hacer que tendieran a cero en magnitud, porque la magnitud finita $ϵ$ solo había servido para permitir un conteo definitivo por el bien del cálculo matemático de probabilidades, y no tenía significado físico. Refiriéndose a una nueva constante universal de la naturaleza, $h$ , Planck supuso que, en los varios osciladores de cada una de las finitas frecuencias características, la energía total se distribuyó a cada uno en un múltiplo entero de una unidad física definida de energía, $ϵ$ , característica de la respectiva frecuencia característica. Su nueva constante universal de la naturaleza, $h$ , ahora se conoce como la constante de Planck.

Planck explicó además que la unidad definida respectiva, $ϵ$ , de energía debe ser proporcional a la frecuencia de oscilación característica respectiva $ν$ del oscilador hipotético, y en 1901 expresó esto con la constante de proporcionalidad $h$ :

{displaystyle epsilon =hnu.}

Planck no propuso que la luz que se propaga en el espacio libre esté cuantificada. La idea de la cuantización del campo electromagnético libre se desarrolló más tarde y finalmente se incorporó a lo que ahora conocemos como teoría cuántica de campos.

En 1906, Planck reconoció que sus resonadores imaginarios, al tener una dinámica lineal, no proporcionaban una explicación física para la transducción de energía entre frecuencias. La física actual explica la transducción entre frecuencias en presencia de átomos por su excitabilidad cuántica, siguiendo a Einstein. Planck creía que en una cavidad con paredes perfectamente reflectantes y sin materia presente, el campo electromagnético no puede intercambiar energía entre componentes de frecuencia. Esto se debe a la linealidad de las ecuaciones de Maxwell. La teoría cuántica de campos actual predice que, en ausencia de materia, el campo electromagnético obedece a ecuaciones no lineales y, en ese sentido, interactúa consigo mismo. Tal interacción en ausencia de materia aún no se ha medido directamente porque requeriría intensidades muy altas y detectores muy sensibles y de bajo ruido, que aún están en proceso de construcción. Planck creía que un campo sin interacciones no obedece ni viola el principio clásico de equipartición de energía y, en cambio, permanece exactamente como estaba cuando se introdujo, en lugar de evolucionar hacia un campo de cuerpo negro. Por lo tanto, la linealidad de sus suposiciones mecánicas impidió que Planck tuviera una explicación mecánica de la maximización de la entropía del campo de radiación térmica del equilibrio termodinámico. Por eso tuvo que recurrir a los argumentos probabilísticos de Boltzmann.

Se puede considerar que la ley de Planck cumple la predicción de Gustav Kirchhoff de que su ley de radiación térmica era de suma importancia. En su presentación madura de su propia ley, Planck ofreció una prueba teórica completa y detallada de la ley de Kirchhoff, cuya prueba teórica hasta entonces había sido debatida a veces, en parte porque se decía que se basaba en objetos teóricos no físicos, como Superficie negra infinitamente fina y perfectamente absorbente de Kirchhoff.

Eventos posteriores

No fue hasta cinco años después de que Planck hiciera su suposición heurística de elementos abstractos de energía o de acción que Albert Einstein concibió los cuantos de luz realmente existentes en 1905 como una explicación revolucionaria de la radiación del cuerpo negro, de la fotoluminiscencia, de la efecto fotoeléctrico, y de la ionización de gases por luz ultravioleta. En 1905, "Einstein creía que no se podía hacer que la teoría de Planck estuviera de acuerdo con la idea de los cuantos de luz, un error que corrigió en 1906". Contrariamente a las creencias de Planck de la época, Einstein propuso un modelo y una fórmula mediante los cuales la luz se emitía, absorbía y propagaba en el espacio libre en cuantos de energía localizados en puntos del espacio. Como introducción a su razonamiento, Einstein recapituló el modelo de Planck de hipotéticos osciladores eléctricos de material resonante como fuentes y sumideros de radiación, pero luego ofreció un nuevo argumento, desconectado de ese modelo, pero basado en parte en un argumento termodinámico de Wien., en el que la fórmula de Planck $ϵ = hν$ no jugó ningún papel. Einstein dio el contenido de energía de tales cuantos en la forma $Rβν / N$ . Así, Einstein contradecía la teoría ondulatoria de la luz sostenida por Planck. En 1910, al criticar un manuscrito que le envió Planck, sabiendo que Planck era un firme partidario de la teoría de la relatividad especial de Einstein, Einstein le escribió a Planck: "Me parece absurdo tener energía distribuida continuamente en espacio sin asumir un éter."

Según Thomas Kuhn, no fue hasta 1908 que Planck aceptó más o menos parte de los argumentos de Einstein a favor de la discreción física a diferencia de la matemática abstracta en la física de la radiación térmica. Todavía en 1908, considerando la propuesta de propagación cuántica de Einstein, Planck opinó que tal paso revolucionario era quizás innecesario. Hasta entonces, Planck había sido coherente al pensar que la discreción de los cuantos de acción no se encontraba ni en sus osciladores resonantes ni en la propagación de la radiación térmica. Kuhn escribió que, en los artículos anteriores de Planck y en su monografía de 1906, no hay 'mención de discontinuidad, [ni] hablar de una restricción en la energía del oscilador, [ni de] ninguna fórmula como $U = nhν$ ." Kuhn señaló que su estudio de los artículos de Planck de 1900 y 1901, y de su monografía de 1906, lo habían llevado a la 'herética' conclusiones, contrariamente a las suposiciones generalizadas de otros que vieron los escritos de Planck solo desde la perspectiva de puntos de vista anacrónicos posteriores. Las conclusiones de Kuhn, encontrando un período hasta 1908, cuando Planck sostuvo consistentemente su 'primera teoría', han sido aceptadas por otros historiadores.

En la segunda edición de su monografía, en 1912, Planck sostuvo su desacuerdo con la propuesta de Einstein de los cuantos de luz. Propuso con cierto detalle que la absorción de luz por sus resonadores de material virtual podría ser continua, ocurriendo a un ritmo constante en equilibrio, a diferencia de la absorción cuántica. Sólo la emisión era cuántica. A esto se le ha llamado en ocasiones la 'segunda teoría' de Planck.

No fue hasta 1919 que Planck en la tercera edición de su monografía más o menos aceptó su 'tercera teoría', que tanto la emisión como la absorción de la luz eran cuánticas.

El colorido término "catástrofe ultravioleta" fue dado por Paul Ehrenfest en 1911 con el resultado paradójico de que la energía total en la cavidad tiende a infinito cuando el teorema de equipartición de la mecánica estadística clásica se aplica (erróneamente) a la radiación del cuerpo negro. Pero esto no había formado parte del pensamiento de Planck, porque no había intentado aplicar la doctrina de la equipartición: cuando hizo su descubrimiento en 1900, no había notado ningún tipo de 'catástrofe'. Fue notado por primera vez por Lord Rayleigh en 1900, y luego en 1901 por Sir James Jeans; y más tarde, en 1905, por Einstein cuando quiso apoyar la idea de que la luz se propaga como paquetes discretos, más tarde llamados 'fotones', y por Rayleigh y por Jeans.

En 1913, Bohr dio otra fórmula con otro significado físico diferente a la cantidad $.$ . En contraste con las fórmulas de Planck y Einstein, la fórmula de Bohr se refirió explícitamente y categóricamente a los niveles de energía de los átomos. La fórmula de Bohr fue $W τ 2 - W τ 1 = .$ Donde $W τ 2$ y $W τ 1$ denota los niveles de energía de estados cuánticos de un átomo, con números cuánticos $τ 2$ y $τ 1$ . El símbolo $.$ denota la frecuencia de un cuántico de radiación que se puede emitir o absorber a medida que el átomo pasa entre esos dos estados cuánticos. En contraste con el modelo de Planck, la frecuencia $nu$ no tiene relación inmediata con las frecuencias que podrían describir esos estados cuánticos.

Más tarde, en 1924, Satyendra Nath Bose desarrolló la teoría de la mecánica estadística de los fotones, que permitió una derivación teórica de la ley de Planck. La palabra real 'fotón' fue inventado aún más tarde, por G.N. Lewis en 1926, quien creía erróneamente que los fotones se conservaban, contrariamente a las estadísticas de Bose-Einstein; sin embargo, la palabra 'fotón' fue adoptado para expresar el postulado de Einstein de la naturaleza de paquete de la propagación de la luz. En un campo electromagnético aislado en el vacío en un recipiente con paredes perfectamente reflectantes, tal como lo consideró Planck, efectivamente los fotones se conservarían según el modelo de Einstein de 1905, pero Lewis se refería a un campo de fotones considerado como un sistema cerrado con respecto a la materia ponderable pero abierto al intercambio de energía electromagnética con un sistema circundante de materia ponderable, e imaginó erróneamente que aún los fotones se conservaban, almacenándose dentro de los átomos.

En última instancia, la ley de Planck de la radiación del cuerpo negro contribuyó al concepto de Einstein de los cuantos de luz portadores de momento lineal, que se convirtió en la base fundamental para el desarrollo de la mecánica cuántica.

La linealidad mencionada anteriormente de los supuestos mecánicos de Planck, que no permiten interacciones energéticas entre los componentes de frecuencia, fue reemplazada en 1925 por la mecánica cuántica original de Heisenberg. En su artículo presentado el 29 de julio de 1925, la teoría de Heisenberg explicaba la fórmula de Bohr de 1913 antes mencionada. Admitía osciladores no lineales como modelos de estados cuánticos atómicos, lo que permitía la interacción energética entre sus propios estados internos múltiples. componentes discretos de frecuencia de Fourier, en las ocasiones de emisión o absorción de cuantos de radiación. La frecuencia de un cuanto de radiación era la de un acoplamiento definido entre estados cuánticos oscilatorios metaestables atómicos internos. En ese momento, Heisenberg no sabía nada de álgebra matricial, pero Max Born leyó el manuscrito del artículo de Heisenberg y reconoció el carácter matricial de la teoría de Heisenberg. Luego, Born y Jordan publicaron una teoría matricial explícita de la mecánica cuántica, basada en la mecánica cuántica original de Heisenberg, pero en una forma claramente diferente de ella; es la teoría matricial de Born y Jordan la que hoy se denomina mecánica matricial. La explicación de Heisenberg de los osciladores de Planck, como efectos no lineales aparentes como modos de Fourier de procesos transitorios de emisión o absorción de radiación, mostró por qué los osciladores de Planck, vistos como objetos físicos duraderos como los que podrían imaginar los la física clásica, no daba una explicación adecuada de los fenómenos.

Hoy en día, como afirmación de la energía de un cuanto de luz, a menudo se encuentra la fórmula $E = ħω$ , donde $ħ = h / 2π$ y $ω = 2π ν$ indica la frecuencia angular y, con menor frecuencia, la fórmula equivalente $E = hν$ . Esta declaración sobre un cuanto de luz que realmente existe y se propaga, basada en la de Einstein, tiene un significado físico diferente al de la declaración anterior de Planck $ϵ = hν$ sobre las unidades de energía abstracta que se distribuirán entre sus hipotéticos osciladores de material resonante.

Un artículo de Helge Kragh publicado en Physics World da cuenta de esta historia.

Contenido relacionado

Más resultados...