Ley de Ohm

V, I, y R, los parámetros de la ley de Ohm

La ley de Ohm establece que la corriente a través de un conductor entre dos puntos es directamente proporcional al voltaje en los dos puntos. Introduciendo la constante de proporcionalidad, la resistencia, se llega a la habitual ecuación matemática que describe esta relación:

I=VR,{displaystyle I={frac {R}} {f}}

donde I es la corriente a través del conductor, V es el voltaje medido a través el conductor y R es la resistencia del conductor. Más específicamente, la ley de Ohm establece que la R en esta relación es constante, independiente de la corriente. Si la resistencia no es constante, la ecuación anterior no puede llamarse ley de Ohm, pero aún puede usarse como una definición de resistencia estática/CC. La ley de Ohm es una relación empírica que describe con precisión la conductividad de la gran mayoría de los materiales conductores de electricidad en muchos órdenes de magnitud de corriente. Sin embargo, algunos materiales no obedecen la ley de Ohm; estos se llaman no óhmicos.

La ley lleva el nombre del físico alemán Georg Ohm, quien, en un tratado publicado en 1827, describió las medidas de tensión y corriente aplicadas a través de circuitos eléctricos simples que contenían varias longitudes de cable. Ohm explicó sus resultados experimentales mediante una ecuación un poco más compleja que la forma moderna anterior (ver § Historia a continuación).

En física, el término ley de Ohm también se usa para referirse a varias generalizaciones de la ley; por ejemplo, la forma vectorial de la ley utilizada en el electromagnetismo y la ciencia de los materiales:

J=σ σ E,{displaystyle mathbf {J} =sigma mathbf {E}

donde J es la densidad de corriente en un lugar determinado en un material resistivo, E es el campo eléctrico en ese lugar y σ (sigma) es un parámetro dependiente del material llamado conductividad. Esta reformulación de la ley de Ohm se debe a Gustav Kirchhoff.

Historia

Georg Ohm

En enero de 1781, antes del trabajo de Georg Ohm, Henry Cavendish experimentó con frascos de Leyden y tubos de vidrio de diferentes diámetros y longitudes llenos de solución salina. Midió la corriente al notar qué tan fuerte fue el impacto que sintió cuando completó el circuito con su cuerpo. Cavendish escribió que la "velocidad" (corriente) varió directamente según el "grado de electrificación" (Voltaje). No comunicó sus resultados a otros científicos en ese momento, y sus resultados fueron desconocidos hasta que Maxwell los publicó en 1879.

Francis Ronalds delineó "intensidad" (voltaje) y "cantidad" (corriente) para la pila seca, una fuente de alto voltaje, en 1814 usando un electrómetro de pan de oro. Encontró para una pila seca que la relación entre los dos parámetros no era proporcional bajo ciertas condiciones meteorológicas.

Ohm hizo su trabajo sobre la resistencia en los años 1825 y 1826, y publicó sus resultados en 1827 como el libro Die galvanische Kette, mathematisch bearbeitet ("El circuito galvánico investigado matemáticamente"). Se inspiró considerablemente en el trabajo de Fourier sobre la conducción del calor en la explicación teórica de su trabajo. Para los experimentos, inicialmente usó pilas voltaicas, pero luego usó un termopar, ya que proporcionaba una fuente de voltaje más estable en términos de resistencia interna y voltaje constante. Usó un galvanómetro para medir la corriente y sabía que el voltaje entre los terminales del termopar era proporcional a la temperatura de la unión. Luego agregó cables de prueba de diferentes longitudes, diámetros y materiales para completar el circuito. Descubrió que sus datos podían modelarse a través de la ecuación

x=ab+l,{displaystyle x={frac {a}{b+l}},}

donde x era la lectura del galvanómetro, l era la longitud del conductor de prueba, a dependía de la temperatura de unión del termopar, y b fue una constante de toda la configuración. A partir de esto, Ohm determinó su ley de proporcionalidad y publicó sus resultados.

Modelo de resistencia interna

En notación moderna escribiríamos,

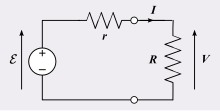
I=Er+R,{displaystyle I={frac {fnMithcal {E}{r+R}} {f}}

Donde E{displaystyle {fnMithcal}} es el circuit emf abierto del termopar, r{displaystyle r} es la resistencia interna del termopar y R{displaystyle R. es la resistencia del alambre de prueba. En términos de la longitud del alambre esto se convierte,

I=Er+Rl,{displaystyle I={frac {fnh} {\fnh} {\fnMithcal {}l}}}} {f}}}

Donde R{displaystyle {fnMithcal}} es la resistencia del alambre de prueba por longitud de unidad. Así, Los coeficientes de Ohm son,

a=ER,b=rR.{displaystyle a={frac {fnMitcal {E} {fnMitcal {R}}},quad b={frac {fnMitcal {} {fnMitcal} {fnMitcal} {fnMitcal} {fnMitcal}} {fnMitcal}} {fnMitcal} {f}}} {fnMitcal}} {fnHFF}}} {fnMitcal}}f}}}}}}}}}} {R}}}

La ley de Georg Ohm en el libro del laboratorio.

La ley de Ohm fue probablemente la más importante de las primeras descripciones cuantitativas de la física de la electricidad. Lo consideramos casi obvio hoy. Cuando Ohm publicó por primera vez su trabajo, este no era el caso; los críticos reaccionaron a su tratamiento del tema con hostilidad. Llamaron a su trabajo una "red de fantasías desnudas" y el Ministro de Educación proclamó que "un profesor que predicaba tales herejías no era digno de enseñar ciencia". La filosofía científica prevaleciente en Alemania en ese momento afirmaba que no es necesario realizar experimentos para desarrollar una comprensión de la naturaleza porque la naturaleza está muy bien ordenada y que las verdades científicas pueden deducirse solo mediante el razonamiento. Además, el hermano de Ohm, Martin, un matemático, estaba luchando contra el sistema educativo alemán. Estos factores dificultaron la aceptación del trabajo de Ohm, y su trabajo no fue ampliamente aceptado hasta la década de 1840. Sin embargo, Ohm recibió reconocimiento por sus contribuciones a la ciencia mucho antes de morir.

En la década de 1850, la ley de Ohm era ampliamente conocida y se consideraba probada. Alternativas como la 'ley de Barlow' quedaron desacreditadas en términos de aplicaciones reales al diseño de sistemas de telégrafo, como lo discutió Samuel F. B. Morse en 1855.

El electrón fue descubierto en 1897 por J. J. Thomson, y rápidamente se dio cuenta de que es la partícula (portador de carga) que transporta las corrientes eléctricas en los circuitos eléctricos. En 1900, Paul Drude propuso el primer modelo (clásico) de conducción eléctrica, el modelo Drude, que finalmente dio una explicación científica de la ley de Ohm. En este modelo, un conductor sólido consta de una red estacionaria de átomos (iones), con electrones de conducción moviéndose aleatoriamente en ella. Un voltaje a través de un conductor provoca un campo eléctrico, que acelera los electrones en la dirección del campo eléctrico, provocando una deriva de electrones que es la corriente eléctrica. Sin embargo, los electrones chocan con los átomos, lo que hace que se dispersen y aleatorice su movimiento, convirtiendo así la energía cinética en calor (energía térmica). Usando distribuciones estadísticas, se puede demostrar que la velocidad de deriva promedio de los electrones y, por lo tanto, la corriente, es proporcional al campo eléctrico y, por lo tanto, al voltaje, en una amplia gama de voltajes.

El desarrollo de la mecánica cuántica en la década de 1920 modificó un poco esta imagen, pero en las teorías modernas aún se puede demostrar que la velocidad de deriva promedio de los electrones es proporcional al campo eléctrico, lo que deriva en la ley de Ohm. En 1927, Arnold Sommerfeld aplicó la distribución cuántica de energías de electrones de Fermi-Dirac al modelo de Drude, lo que resultó en el modelo de electrones libres. Un año después, Felix Bloch demostró que los electrones se mueven en ondas (electrones de Bloch) a través de una red cristalina sólida, por lo que la dispersión de los átomos de la red como se postula en el modelo de Drude no es un proceso importante; los electrones dispersan átomos de impurezas y defectos en el material. El sucesor final, la moderna teoría cuántica de bandas de sólidos, demostró que los electrones en un sólido no pueden adquirir ninguna energía como se supone en el modelo de Drude, sino que están restringidos a bandas de energía, con espacios entre ellas de energías que los electrones tienen prohibido tener. El tamaño de la banda prohibida es una característica de una sustancia en particular que tiene mucho que ver con su resistividad eléctrica, lo que explica por qué algunas sustancias son conductoras eléctricas, algunas semiconductoras y algunas aislantes.

Aunque todavía se usa el antiguo término para la conductancia eléctrica, el mho (el inverso de la unidad de resistencia ohm), en 1971 se adoptó un nuevo nombre, siemens, en honor a Ernst Werner von Siemens. Se prefiere el siemens en papeles formales.

En la década de 1920, se descubrió que la corriente a través de una resistencia práctica en realidad tiene fluctuaciones estadísticas, que dependen de la temperatura, incluso cuando el voltaje y la resistencia son exactamente constantes; esta fluctuación, ahora conocida como ruido de Johnson-Nyquist, se debe a la naturaleza discreta de la carga. Este efecto térmico implica que las mediciones de corriente y voltaje que se toman durante períodos de tiempo suficientemente cortos producirán relaciones de V/I que fluctúan desde el valor de R implícito por el promedio de tiempo o el promedio de conjunto de la corriente medida; La ley de Ohm sigue siendo correcta para la corriente promedio, en el caso de materiales resistivos ordinarios.

El trabajo de Ohm precedió por mucho tiempo a las ecuaciones de Maxwell y a cualquier comprensión de los efectos dependientes de la frecuencia en los circuitos de CA. Los desarrollos modernos en teoría electromagnética y teoría de circuitos no contradicen la ley de Ohm cuando se evalúan dentro de los límites apropiados.

Alcance

La ley de Ohm es una ley empírica, una generalización de muchos experimentos que han demostrado que la corriente es aproximadamente proporcional al campo eléctrico para la mayoría de los materiales. Es menos fundamental que las ecuaciones de Maxwell y no siempre se cumple. Cualquier material dado se descompondrá bajo un campo eléctrico lo suficientemente fuerte, y algunos materiales de interés en ingeniería eléctrica son "no óhmicos" bajo campos débiles.

La ley de Ohm se ha observado en una amplia gama de escalas de longitud. A principios del siglo XX, se pensó que la ley de Ohm fallaría a escala atómica, pero los experimentos no han confirmado esta expectativa. A partir de 2012, los investigadores han demostrado que la ley de Ohm funciona para cables de silicio tan pequeños como cuatro átomos de ancho y un átomo de alto.

Orígenes microscópicos

Los electrones modelo Drude (se muestran aquí en azul) rebotan constantemente entre iones de cristal más pesados (se muestran en rojo).

La dependencia de la densidad de corriente del campo eléctrico aplicado es esencialmente de naturaleza mecánica cuántica; (consulte Conductividad clásica y cuántica). Una descripción cualitativa que conduzca a la ley de Ohm se puede basar en la mecánica clásica utilizando el modelo Drude desarrollado por Paul Drude en 1900.

El modelo Drude trata a los electrones (u otros portadores de carga) como bolas de billar que rebotan entre los iones que forman la estructura del material. Los electrones serán acelerados en dirección opuesta al campo eléctrico por el campo eléctrico promedio en su ubicación. Sin embargo, con cada colisión, el electrón se desvía en una dirección aleatoria con una velocidad que es mucho mayor que la velocidad ganada por el campo eléctrico. El resultado neto es que los electrones toman un camino en zigzag debido a las colisiones, pero generalmente se desplazan en una dirección opuesta al campo eléctrico.

La velocidad de deriva determina la densidad de corriente eléctrica y su relación con E y es independiente de las colisiones. Drude calculó la velocidad de deriva promedio desde p = −eEτ donde p es el momento promedio, −e es la carga del electrón y τ es el tiempo promedio entre las colisiones. Dado que tanto el impulso como la densidad de corriente son proporcionales a la velocidad de deriva, la densidad de corriente se vuelve proporcional al campo eléctrico aplicado; esto conduce a la ley de Ohm.

Analogía hidráulica

A veces se usa una analogía hidráulica para describir la ley de Ohm. La presión del agua, medida en pascales (o PSI), es el análogo del voltaje porque establecer una diferencia de presión de agua entre dos puntos a lo largo de una tubería (horizontal) hace que el agua fluya. La tasa de flujo de volumen de agua, en litros por segundo, es el análogo de la corriente, en coulombs por segundo. Finalmente, los restrictores de flujo, como las aberturas colocadas en las tuberías entre los puntos donde se mide la presión del agua, son el análogo de las resistencias. Decimos que la tasa de flujo de agua a través de un restrictor de apertura es proporcional a la diferencia en la presión del agua a través del restrictor. De manera similar, la tasa de flujo de carga eléctrica, es decir, la corriente eléctrica, a través de una resistencia eléctrica es proporcional a la diferencia de voltaje medida a través de la resistencia. De manera más general, la carga hidráulica puede tomarse como el análogo del voltaje, y la ley de Ohm es entonces análoga a la ley de Darcy, que relaciona la carga hidráulica con el caudal volumétrico a través de la conductividad hidráulica.

Las variables de flujo y presión se pueden calcular en una red de flujo de fluidos con el uso de la analogía del ohmio hidráulico. El método se puede aplicar tanto a situaciones de flujo constante como transitorio. En la región de flujo laminar lineal, la ley de Poiseuille describe la resistencia hidráulica de una tubería, pero en la región de flujo turbulento las relaciones presión-flujo se vuelven no lineales.

La analogía hidráulica con la ley de Ohm se ha utilizado, por ejemplo, para aproximar el flujo sanguíneo a través del sistema circulatorio.

Análisis de circuitos

Cubrir lo desconocido en la imagen mnemónica de la ley de Ohm da la fórmula en términos de los parámetros restantes

Rueda de derecho de Ohm con símbolos de unidad internacional

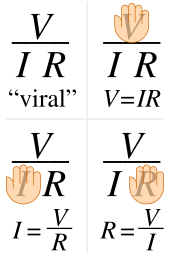
En el análisis de circuitos, se usan indistintamente tres expresiones equivalentes de la ley de Ohm:

I=VRoV=IRoR=VI.{displaystyle I={frac {fnK}f}fnK}quad V=IRquad {text{or}quad R={frac} - Sí.

Algunas fuentes citan cada ecuación como la relación definitoria de la ley de Ohm, o los tres están citados, o se derivan de una forma proporcional, o incluso solo los dos que no corresponden a la declaración original de Ohm a veces se pueden dar.

La intercambiabilidad de la ecuación se puede representar mediante un triángulo, donde V (voltaje) se coloca en la sección superior, I (corriente) se coloca en la parte superior la sección izquierda, y la R (resistencia) se coloca a la derecha. El divisor entre las secciones superior e inferior indica división (de ahí la barra de división).

Circuitos resistivos

Los resistores son elementos de circuito que impiden el paso de carga eléctrica de acuerdo con la ley de Ohm y están diseñados para tener un valor de resistencia específico R. En los diagramas esquemáticos, una resistencia se muestra como un rectángulo largo o un símbolo en zig-zag. Un elemento (resistencia o conductor) que se comporta de acuerdo con la ley de Ohm en algún rango operativo se denomina dispositivo óhmico (o una resistencia óhmica) porque Ohm& La ley de #39 y un solo valor para la resistencia son suficientes para describir el comportamiento del dispositivo en ese rango.

La ley de Ohm se aplica a los circuitos que contienen solo elementos resistivos (sin capacitancias ni inductancias) para todas las formas de tensión o corriente de activación, independientemente de si la tensión o la corriente de activación son constantes (CC) o variables en el tiempo, como C.A. En cualquier instante de tiempo la ley de Ohm es válida para tales circuitos.

Las resistencias que están en serie o en paralelo se pueden agrupar en una sola "resistencia equivalente" para aplicar la ley de Ohm en el análisis del circuito.

Circuitos reactivos con señales variables en el tiempo

Cuando elementos reactivos como capacitores, inductores o líneas de transmisión están involucrados en un circuito al que se aplica CA o voltaje o corriente variable en el tiempo, la relación entre voltaje y corriente se convierte en la solución a una ecuación diferencial, por lo que Ohm&# La ley de 39 (como se definió anteriormente) no se aplica directamente ya que esa forma contiene solo resistencias que tienen un valor R, no impedancias complejas que pueden contener capacitancia (C) o inductancia (L).

Las ecuaciones para circuitos de CA invariantes en el tiempo toman la misma forma que la ley de Ohm. Sin embargo, las variables se generalizan a números complejos y las formas de onda de corriente y voltaje son exponenciales complejas.

En este enfoque, una forma de onda de voltaje o corriente toma la forma Ae^st, donde t es el tiempo, s es un parámetro complejo y A es un escalar complejo. En cualquier sistema lineal invariable en el tiempo, todas las corrientes y voltajes se pueden expresar con el mismo parámetro s que la entrada al sistema, lo que permite cancelar el término exponencial complejo variable en el tiempo y sistema descrito algebraicamente en términos de escalares complejos en las formas de onda de corriente y voltaje.

La generalización compleja de la resistencia es la impedancia, generalmente denominada Z; se puede demostrar que para un inductor,

Z=sL{displaystyle Z=sL

y para un condensador,

Z=1sC.{displaystyle Z={frac {1}{sC}.}

Ahora podemos escribir,

V=ZI{displaystyle V=Z,I}

donde V e I son los escalares complejos en el voltaje y la corriente respectivamente y Z es la impedancia compleja.

Esta forma de la ley de Ohm, con Z en lugar de R, generaliza la forma más simple. Cuando Z es complejo, sólo la parte real se encarga de disipar el calor.

En un circuito de CA general, Z varía mucho con el parámetro de frecuencia s, al igual que la relación entre voltaje y corriente.

Para el caso común de un sinusoide constante, el s el parámetro se toma j⋅ ⋅ {displaystyle jomega }, correspondiente a un complejo sinusoide Aej⋅ ⋅ t{displaystyle Ae^{mbox{}jomega t}. Las partes reales de estas complejas ondas de corriente y voltaje describen las corrientes y voltajes sinusoidales reales en un circuito, que pueden estar en diferentes fases debido a los diferentes escalares complejos.

Aproximaciones lineales

La ley de Ohm es una de las ecuaciones básicas utilizadas en el análisis de circuitos eléctricos. Se aplica tanto a los conductores metálicos como a los componentes del circuito (resistencias) fabricados específicamente para este comportamiento. Ambos son omnipresentes en la ingeniería eléctrica. Los materiales y componentes que obedecen la ley de Ohm se describen como "óhmicos" lo que significa que producen el mismo valor de resistencia (R = V/I) independientemente del valor de V o I que se aplica y si el voltaje o la corriente aplicada es CC (corriente continua) de polaridad positiva o negativa o CA (corriente alterna).

En un dispositivo óhmico verdadero, el mismo valor de resistencia se calculará a partir de R = V/I independientemente del valor de la tensión aplicada V. Es decir, la relación de V/I es constante, y cuando la corriente se grafica como función del voltaje, la curva es lineal (una recta línea). Si el voltaje se fuerza a algún valor V, entonces ese voltaje V dividido por la corriente medida I será igual a R. O si la corriente se fuerza a algún valor I, entonces el voltaje medido V dividido por esa corriente I también es R. Dado que la gráfica de I versus V es una línea recta, entonces también es cierto que para cualquier conjunto de dos voltajes diferentes V ₁ y V₂ aplicados a través de un dispositivo dado de resistencia R, produciendo corrientes I₁ = V₁/R y I₂ = V₂/R, que la relación (V₁ − V₂)/(I₁ − I₂) es también una constante igual a R. El operador "delta" (Δ) se usa para representar una diferencia en una cantidad, por lo que podemos escribir ΔV = V₁ − V₂ y ΔI = I₁ − I₂ . Resumiendo, para cualquier dispositivo verdaderamente óhmico que tenga una resistencia R, V/I = ΔV/Δ I = R para cualquier tensión o corriente aplicada o para la diferencia entre cualquier conjunto de tensiones o corrientes aplicadas.

Las curvas I-V de cuatro dispositivos: Dos resistencias, un diodo y una batería. Los dos resistores siguen la ley de Ohm: La trama es una línea recta a través del origen. Los otros dos dispositivos sí no seguir La ley de Ohm.

Hay, sin embargo, componentes de circuitos eléctricos que no obedecen la ley de Ohm; es decir, su relación entre corriente y voltaje (su curva I–V) es no lineal (o no óhmica). Un ejemplo es el diodo de unión p-n (curva a la derecha). Como se ve en la figura, la corriente no aumenta linealmente con el voltaje aplicado a un diodo. Se puede determinar un valor de corriente (I) para un valor dado de voltaje aplicado (V) a partir de la curva, pero no a partir de la ley de Ohm, ya que la valor de "resistencia" no es constante en función del voltaje aplicado. Además, la corriente solo aumenta significativamente si el voltaje aplicado es positivo, no negativo. La relación V/I para algún punto a lo largo de la curva no lineal a veces se denomina estática, o cordal, o CC, resistencia, pero como se ve en la figura, el valor del V total sobre el I total varía según el punto particular a lo largo de la curva no lineal que se elija. Esto significa que la "resistencia de CC" V/I en algún punto de la curva no es lo mismo que lo que se determinaría aplicando una señal de CA con una amplitud máxima de ΔV voltios o ΔI amperios centrada en ese punto. mismo punto a lo largo de la curva y midiendo ΔV/ΔI. Sin embargo, en algunas aplicaciones de diodos, la señal de CA aplicada al dispositivo es pequeña y es posible analizar el circuito en términos de dinámica, pequeña señal o incremental, definida como aquella sobre la pendiente de la curva V–I en el valor promedio (punto de operación DC) del voltaje (que es decir, uno sobre la derivada de la corriente con respecto al voltaje). Para señales suficientemente pequeñas, la resistencia dinámica permite calcular la resistencia de señal pequeña de la ley de Ohm como aproximadamente uno sobre la pendiente de una línea trazada tangencialmente a V–I curva en el punto de operación DC.

Efectos de temperatura

La ley de Ohm se ha establecido a veces como "para un conductor en un estado dado, la fuerza electromotriz es proporcional a la corriente producida". Es decir, que la resistencia, la relación entre la fuerza electromotriz aplicada (o voltaje) y la corriente, "no varía con la intensidad de la corriente". El calificador "en un estado determinado" generalmente se interpreta en el sentido de "a una temperatura constante," ya que la resistividad de los materiales suele depender de la temperatura. Debido a que la conducción de la corriente está relacionada con el calentamiento por Joule del cuerpo conductor, de acuerdo con la primera ley de Joule, la temperatura de un cuerpo conductor puede cambiar cuando transporta una corriente. Por lo tanto, la dependencia de la resistencia con la temperatura hace que la resistencia dependa de la corriente en una configuración experimental típica, lo que hace que la ley en esta forma sea difícil de verificar directamente. Maxwell y otros desarrollaron varios métodos para probar la ley experimentalmente en 1876, controlando los efectos de calentamiento.

Relación con las conducciones de calor

El principio de Ohm predice el flujo de carga eléctrica (es decir, corriente) en los conductores eléctricos cuando se someten a la influencia de las diferencias de voltaje; El principio de Jean-Baptiste-Joseph Fourier predice el flujo de calor en los conductores de calor cuando se someten a la influencia de las diferencias de temperatura.

La misma ecuación describe ambos fenómenos, y las variables de la ecuación adquieren significados diferentes en los dos casos. Específicamente, resolver un problema de conducción de calor (Fourier) con temperatura (la "fuerza" impulsora) y flujo de calor (la tasa de flujo de la impulsión "cantidad", es decir, energía térmica) también resuelve un problema análogo de conducción eléctrica (Ohm) que tiene potencial eléctrico (la "fuerza motriz") y corriente eléctrica (la tasa de flujo de la "cantidad" impulsada, es decir, carga) variables.

La base del trabajo de Fourier fue su clara concepción y definición de la conductividad térmica. Asumió que, siendo todo lo demás igual, el flujo de calor es estrictamente proporcional al gradiente de temperatura. Aunque sin duda es cierto para pequeños gradientes de temperatura, el comportamiento estrictamente proporcional se perderá cuando los materiales reales (por ejemplo, aquellos que tienen una conductividad térmica que es función de la temperatura) se someten a grandes gradientes de temperatura.

Se hace una suposición similar en la declaración de la ley de Ohm: siendo todo lo demás similar, la fuerza de la corriente en cada punto es proporcional al gradiente de potencial eléctrico. La precisión de la suposición de que el flujo es proporcional al gradiente se prueba más fácilmente, usando métodos de medición modernos, para el caso eléctrico que para el caso de calor.

Otras versiones

La ley de Ohm, en la forma anterior, es una ecuación extremadamente útil en el campo de la ingeniería eléctrica/electrónica porque describe cómo se interrelacionan el voltaje, la corriente y la resistencia en un "macroscópico" nivel, es decir, comúnmente, como elementos de circuito en un circuito eléctrico. Los físicos que estudian las propiedades eléctricas de la materia a nivel microscópico utilizan una ecuación vectorial más general y estrechamente relacionada, a veces también denominada ley de Ohm, que tiene variables que están estrechamente relacionadas con las variables escalares V, I y R. de la ley de Ohm, pero que son funciones de posición dentro del conductor. Los físicos suelen utilizar esta forma continua de la ley de Ohm:

E=*** *** J{displaystyle mathbf {E} =rho mathbf {J}

DondeE"es el vector de campo eléctrico con unidades de voltios por metro (analógico a "V" de la ley de Ohm que tiene unidades de voltios), "J" es el vector de densidad actual con unidades de amperios por área unitaria (analógico a "I" de la ley de Ohm que tiene unidades de amperios), y "ρ" (Greek "rho") es la resistividad con unidades de ohm·meters (analógico a "R" de la ley de Ohm que tiene unidades de ohms). La ecuación anterior se escribe a veces como J = σ σ {displaystyle sigma }E donde "σ" (Greek "sigma") es la conductividad que es la reciprocal de ρ.

Corriente corriente a través de un conductor cilíndrico uniforme (como un alambre redondo) con un campo uniforme aplicado.

El voltaje entre dos puntos se define como:

Δ Δ V=− − ∫ ∫ E⋅ ⋅ dl{displaystyle {Delta V}=- {fnMithbf {E}cdot dmathbf {l}}

con dl{displaystyle dmathbf} el elemento del camino a lo largo de la integración del vector de campo eléctrico E. Si se aplica E campo es uniforme y orientado a lo largo de la longitud del conductor como se muestra en la figura, luego definiendo el voltaje V en la convención habitual de ser opuesto en dirección al campo (ver figura), y con el entendimiento de que el voltaje V se mide de forma diferencial a través de la longitud del conductor que nos permite bajar el símbolo Δ, la ecuación vector anterior reduce a la ecuación escalar:

V=EloE=Vl.{displaystyle V={E}{l} {text{or} E={frac {V}}}.

Dado que el campo E es uniforme en la dirección de la longitud del cable, para un conductor que tenga una resistividad ρ uniformemente consistente, la densidad de corriente J también será uniforme en cualquier cruce -área de la sección y orientada en la dirección de la longitud del cable, por lo que podemos escribir:

J=Ia.{displaystyle J={frac {I}{a}}

Sustituyendo los 2 resultados anteriores (para E y J respectivamente) en la forma continua que se muestra al principio de esta sección:

Vl=Ia*** *** oV=I*** *** la.{displaystyle {frac}={frac} {I}{a}rho qquad {text{or}qquad V=Irho {frac {I}{a}}

La resistencia eléctrica de un conductor uniforme viene dada en términos de resistividad por:

R=*** *** la{displaystyle {R}=rho {fnMicroc} {I}{a}}

donde l es la longitud del conductor en unidades SI de metros, a es el área de la sección transversal (para un alambre redondo a = πr² si r es radio) en unidades de metros cuadrados, y ρ es la resistividad en unidades de ohm·metros.

Después de sustituir R de la ecuación anterior en la ecuación que la precede, la forma continua de la ley de Ohm para un campo uniforme (y una densidad de corriente uniforme) orientada a lo largo de la longitud del conductor se reduce a la forma más familiar:

V=IR.{displaystyle {V}={I} {R}}

Una red cristalina perfecta, con un movimiento térmico lo suficientemente bajo y sin desviaciones de la estructura periódica, no tendría resistividad, pero un metal real tiene defectos cristalográficos, impurezas, múltiples isótopos y movimiento térmico de los átomos. Los electrones se dispersan de todos estos, lo que resulta en una resistencia a su flujo.

Las formas generalizadas más complejas de la ley de Ohm son importantes para la física de la materia condensada, que estudia las propiedades de la materia y, en particular, su estructura electrónica. En términos generales, caen bajo el tema de las ecuaciones constitutivas y la teoría de los coeficientes de transporte.

Efectos magnéticos

Si está presente un campo B externo y el conductor no está en reposo sino moviéndose a una velocidad v, entonces se debe agregar un término adicional para tener en cuenta la corriente inducida por la fuerza de Lorentz sobre los portadores de carga.

J=σ σ ()E+v× × B){displaystyle mathbf {J} =sigma (mathbf {E} +mathbf {v} times mathbf {B}}

En el marco de reposo del conductor en movimiento este término desaparece porque v= 0. No hay contradicción porque el campo eléctrico en el marco de reposo difiere del E -campo en el cuadro de laboratorio: E′ = E + v×B. Los campos eléctrico y magnético son relativos, véase la transformación de Lorentz.

Si la corriente J es alterna porque el voltaje aplicado o el campo E varía con el tiempo, entonces se debe agregar la reactancia a la resistencia para tener en cuenta la autoinducción, consulte impedancia eléctrica La reactancia puede ser fuerte si la frecuencia es alta o si el conductor está enrollado.

Fluidos conductores

En un líquido conductivo, como un plasma, hay un efecto similar. Considere un líquido que se mueve con la velocidad v{displaystyle mathbf {v} en un campo magnético B{displaystyle mathbf {B}. El movimiento relativo induce un campo eléctrico E{displaystyle mathbf {E} que ejerce fuerza eléctrica sobre las partículas cargadas dando lugar a una corriente eléctrica J{displaystyle mathbf {J}. La ecuación del movimiento para el gas de electrones, con una densidad de número ne{displaystyle n_{e}, está escrito como

menedvedt=− − neeE+neme.. ()vi− − ve)− − eneve× × B,{displaystyle m_{e}n_{e}{dmathbf {v} _{e} over dt=-n_{e}emathbf {E} +n_{e}m_{e}nu (mathbf {v}-Mathbf {v})-en_{e}mathbf {v} _{e}times mathbf {B}

Donde e{displaystyle e}, me{displaystyle m_{e} y ve{displaystyle mathbf {v} _{e} son la carga, masa y velocidad de los electrones, respectivamente. También, .. {displaystyle nu } es la frecuencia de colisiones de los electrones con iones que tienen un campo de velocidad vi{displaystyle mathbf {v} _{i}. Desde entonces, el electrón tiene una masa muy pequeña en comparación con la de iones, podemos ignorar el lado izquierdo de la ecuación anterior para escribir

σ σ ()E+v× × B)=J,{displaystyle sigma (mathbf {E} +mathbf {v} times mathbf {B})=mathbf {J}

donde hemos utilizado la definición de la densidad actual, y también poner σ σ =nee2.. me{displaystyle sigma ={n_{e}e^{2} over nu m_{e}} que es la conductividad eléctrica. Esta ecuación también se puede escribir equivalentemente como

E+v× × B=*** *** J,{displaystyle mathbf {E} +mathbf {v} times mathbf {B} =rho mathbf {J}

Donde *** *** =σ σ − − 1{displaystyle rho =sigma ^{-1} es la resistencia eléctrica. También es común escribir .. {displaystyle eta } en lugar de *** *** {displaystyle rho } que puede ser confuso ya que es la misma notación utilizada para la difusión magnética definida como .. =1/μ μ 0σ σ {displaystyle eta =1/mu ¿Qué?.

Enlaces externos y lecturas adicionales