Ley de los gases ideales

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ecuación del estado de un gas ideal hipotético

Isotherms of an ideal gas for different temperatures. Las líneas curvas son hiperbolas rectangulares de la forma y = a/x. Representan la relación entre la presión (en el eje vertical) y el volumen (en el eje horizontal) para un gas ideal a diferentes temperaturas: líneas que están más lejos del origen (es decir, líneas que están más cerca de la esquina superior derecha del diagrama) corresponden a temperaturas superiores.

La ley de los gases ideales, también llamada ecuación general de los gases, es la ecuación de estado de un gas ideal hipotético. Es una buena aproximación del comportamiento de muchos gases bajo muchas condiciones, aunque tiene varias limitaciones. Fue declarado por primera vez por Benoît Paul Émile Clapeyron en 1834 como una combinación de la ley empírica de Boyle, la ley de Charles, la ley de Avogadro y la ley de Gay-Lussac. La ley de los gases ideales a menudo se escribe en forma empírica:

{displaystyle pV=nRT}

p

V

T

n

R

Ecuación

Las colisiones moleculares dentro de un contenedor cerrado (un tanque de propano) se muestran (derecha). Las flechas representan los movimientos aleatorios y las colisiones de estas moléculas. La presión y la temperatura del gas son directamente proporcionales: A medida que aumenta la temperatura, la presión del gas propano aumenta por el mismo factor. Una consecuencia simple de esta proporcionalidad es que en un día de verano caliente, la presión del tanque de propano será elevada, y por lo tanto los tanques de propano deben ser calificados para soportar tales aumentos de presión.

El estado de una cantidad de gas está determinado por su presión, volumen y temperatura. La forma moderna de la ecuación los relaciona simplemente en dos formas principales. La temperatura utilizada en la ecuación de estado es una temperatura absoluta: la unidad SI apropiada es el kelvin.

Formas comunes

Las formas introducidas con mayor frecuencia son:

{displaystyle pV=nRT=nk_{text{B}}N_{text{A}}T=Nk_{text{B}}T}

$p$ es la presión absoluta del gas,
$V$ es el volumen del gas,
$n$ es la cantidad de sustancia de gas (también conocido como número de lunares),
$R$ es el ideal, o universal, constante de gas, igual al producto de la constante Boltzmann y la constante Avogadro,
$k_{text{B}}$ es la constante de Boltzmann,
$N_{{A}}$ es la constante Avogadro,
$T$ es la temperatura absoluta del gas,
$N$ es el número de partículas (normalmente átomos o moléculas) del gas.

En unidades SI, p se mide en pascales, V se mide en metros cúbicos, n se mide en moles y T en kelvins (la escala Kelvin es una escala Celsius desplazada, donde 0,00 K = −273,15 °C, la temperatura más baja posible). R tiene por valor 8,314 J/(mol·K) = 1,989 ≈ 2 cal/(mol·K), o 0,0821 L⋅atm/(mol⋅K).

Forma molar

La cantidad de gas presente podría especificarse dando la masa en lugar de la cantidad química de gas. Por lo tanto, puede ser útil una forma alternativa de la ley de los gases ideales. La cantidad química, n (en moles), es igual a la masa total del gas (m) (en kilogramos) dividida por la masa molar, M (en kilogramos por mol):

{displaystyle n={frac {m}{M}}.}

Reemplazando n con m/M y posteriormente introduciendo densidad ρ = m/V, obtenemos:

{displaystyle pV={frac {m}{M}}RT}

{displaystyle p={frac {m}{V}}{frac {RT}{M}}}

{displaystyle p=rho {frac {R}{M}}T}

Definiendo la constante de gas específica R_{específica(r)} como la relación R/M ,

{displaystyle p=rho R_{text{specific}}T}

Esta forma de la ley de los gases ideales es muy útil porque vincula la presión, la densidad y la temperatura en una fórmula única independiente de la cantidad del gas considerado. Alternativamente, la ley puede escribirse en términos del volumen específico v, el recíproco de la densidad, como

{displaystyle pv=R_{text{specific}}T.}

Es común, especialmente en aplicaciones de ingeniería y meteorología, representar a la específico constante de gas por el símbolo R. En tales casos, universal la constante de gas generalmente se da un símbolo diferente como ${displaystyle {bar {R}}}$ o $R^{*}$ para distinguirlo. En cualquier caso, el contexto y/o unidades de la constante de gas debe dejar claro si se está utilizando la constante de gas universal o específica.

Mecánica estadística

En mecánica estadística, la siguiente ecuación molecular se deriva de los primeros principios

{displaystyle P=nk_{text{B}}T,}

donde $P$ es la presión absoluta del gas, $n$ es la densidad numérica de las moléculas (dada por la relación $n = N / V$ , en contraste con la formulación anterior en la que $n$ es el número de moles), $T$ es la temperatura absoluta, y $k B$ es la constante de Boltzmann que relaciona temperatura y energía, dada por:

{displaystyle k_{text{B}}={frac {R}{N_{text{A}}}}}

donde $N A$ es la constante de Avogadro.

De esto notamos que para un gas de masa $m$ , con una masa de partícula promedio de $μ$ por la constante de masa atómica, $m u$ , (es decir, la masa es $μ$ u) el número de moléculas vendrá dado por

{displaystyle N={frac {m}{mu m_{text{u}}}},}

y desde $ρ = m / V = nμm u$ , encontramos que la ley de los gases ideales se puede reescribir como

{displaystyle P={frac {1}{V}}{frac {m}{mu m_{text{u}}}}k_{text{B}}T={frac {k_{text{B}}}{mu m_{text{u}}}}rho T.}

En unidades SI, $P$ se mide en pascales, $V$ en metros cúbicos, $T$ en kelvins y $k B = 1.38 \times 10 -23 J\cdotK -1$ en unidades SI.

Ley de los gases combinados

Combinar las leyes de Charles, Boyle y Gay-Lussac da la Derecho combinado de gas, que toma la misma forma funcional que la ley de gas ideal dice que el número de moles no es especificado, y la relación de $PV$ a $T$ simplemente se toma como una constante:

{displaystyle {frac {PV}{T}}=k,}

Donde $P$ es la presión del gas, $V$ es el volumen del gas, $T$ es la temperatura absoluta del gas, y $k$ es una constante. Al comparar la misma sustancia en dos conjuntos diferentes de condiciones, la ley puede ser escrita como

{displaystyle {frac {P_{1}V_{1}}{T_{1}}}={frac {P_{2}V_{2}}{T_{2}}}.}

Energía asociada a un gas

De acuerdo con los supuestos de la teoría cinética de los gases ideales, se puede considerar que no existen atracciones intermoleculares entre las moléculas, o átomos, de un gas ideal. En otras palabras, su energía potencial es cero. Por lo tanto, toda la energía que posee el gas es la energía cinética de las moléculas o átomos del gas.

{displaystyle E={frac {3}{2}}nRT}

Esto corresponde a la energía cinética de n moles de un gas monoatómico que tiene 3 grados de libertad; x, y, z. La siguiente tabla muestra esta relación para diferentes cantidades de un gas monoatómico.

Energía de un gas monoatámico	Expresión matemática
Energía asociada con un topo	${displaystyle E={frac {3}{2}}RT}$
Energía asociada a un gramo	${displaystyle E={frac {3}{2}}rT}$
Energía asociada con un átomo	${displaystyle E={frac {3}{2}}k_{B}T}$

Aplicaciones a procesos termodinámicos

La siguiente tabla esencialmente simplifica la ecuación del gas ideal para un proceso particular, lo que hace que esta ecuación sea más fácil de resolver usando métodos numéricos.

Un proceso termodinámico se define como un sistema que se mueve del estado 1 al estado 2, donde el número de estado se indica mediante un subíndice. Como se muestra en la primera columna de la tabla, los procesos termodinámicos básicos se definen de tal manera que una de las propiedades del gas (P, V, T, S, o H) es constante durante todo el proceso.

Para un proceso termodinámico determinado, con el fin de especificar el alcance de un proceso en particular, se debe especificar una de las relaciones de propiedades (que se enumeran en la columna etiquetada como "relación conocida") (ya sea directamente o indirectamente). Además, la propiedad para la cual se conoce la relación debe ser distinta de la propiedad mantenida constante en la columna anterior (de lo contrario, la relación sería la unidad y no habría suficiente información disponible para simplificar la ecuación de la ley de los gases).

En las últimas tres columnas, las propiedades (p, V o T) en el estado 2 se pueden calcular a partir de las propiedades en estado 1 utilizando las ecuaciones enumeradas.

Proceso	Constante	Relación conocida o delta	p₂	V₂	T₂
Proceso de Isobaric	Presión	V₂/V₁	p₂ = p₁	V₂ V₁(V)₂/V₁)	T₂ T₁(V)₂/V₁)
Proceso de Isobaric	Presión	T₂/T₁	p₂ = p₁	V₂ V₁(T₂/T₁)	T₂ T₁(T₂/T₁)
Proceso de Isocoric (Proceso isovolumétrico) (Proceso Isométrico)	Volumen	p₂/p₁	p₂ = p₁(p₂/p₁)	V₂ V₁	T₂ T₁(p₂/p₁)
	Volumen	T₂/T₁	p₂ = p₁(T₂/T₁)	V₂ V₁	T₂ T₁(T₂/T₁)
Proceso intrastémico	Temperatura	p₂/p₁	p₂ = p₁(p₂/p₁)	V₂ V₁/(p)₂/p₁)	T₂ T₁
Proceso intrastémico	Temperatura	V₂/V₁	p₂ = p₁/(V)₂/V₁)	V₂ V₁(V)₂/V₁)	T₂ T₁
Proceso Isentrópico (Proceso adiabático revisible)	Entropy	p₂/p₁	p₂ = p₁(p₂/p₁)	V₂ V₁(p₂/p₁)^(1−1/γ)	T₂ T₁(p₂/p₁)^{(γ −1)/γ}
		V₂/V₁	p₂ = p₁(V)₂/V₁)^γ	V₂ V₁(V)₂/V₁)	T₂ T₁(V)₂/V₁)^{(1 − γ)}
		T₂/T₁	p₂ = p₁(T₂/T₁)^{γ/(γ - 1)}	V₂ V₁(T₂/T₁)^{1/(1 − γ)}	T₂ T₁(T₂/T₁)
Proceso politrópico	P Vⁿ	p₂/p₁	p₂ = p₁(p₂/p₁)	V₂ V₁(p₂/p₁)^{(1 - 1n)}	T₂ T₁(p₂/p₁)^{()n −1)/n}
		V₂/V₁	p₂ = p₁(V)₂/V₁)⁻ⁿ	V₂ V₁(V)₂/V₁)	T₂ T₁(V)₂/V₁)^{(1 − n)}
		T₂/T₁	p₂ = p₁(T₂/T₁)^{n/(n −1)}	V₂ V₁(T₂/T₁)^{1/(1 − n)}	T₂ T₁(T₂/T₁)
Proceso idental (Proceso adiabático irreversible)	Enthalpy	p₂ −₁	p₂ = p₁ + (p₂ −₁)		T₂ T₁ + μ_JT(p₂ −₁)
Proceso idental (Proceso adiabático irreversible)	Enthalpy	T₂ − T₁	p₂ = p₁ + (T₂ − T₁)/μ_JT		T₂ T₁ + (T₂ − T₁)

^ a. En un proceso isoentrópico, la entropía del sistema (S) es constante. Bajo estas condiciones, p₁V₁^γ = p₂V₂^γ, donde γ se define como la relación de capacidad calorífica, que es constante para un gas caloríficamente perfecto. El valor utilizado para γ suele ser 1,4 para gases diatómicos como nitrógeno (N₂) y oxígeno (O₂), (y aire, que es 99% diatómico). Además, γ suele ser 1,6 para gases monoatómicos como los gases nobles helio (He) y argón (Ar). En los motores de combustión interna γ varía entre 1,35 y 1,15, dependiendo de la constitución de los gases y la temperatura.

^ b. En un proceso isoentálpico, la entalpía del sistema (H) es constante. En el caso de expansión libre para un gas ideal, no hay interacciones moleculares y la temperatura permanece constante. Para los gases reales, las moléculas interactúan a través de la atracción o la repulsión según la temperatura y la presión, y se produce calentamiento o enfriamiento. Esto se conoce como el efecto Joule-Thomson. Como referencia, el coeficiente de Joule-Thomson μ_JT para el aire a temperatura ambiente y al nivel del mar es de 0,22 °C/bar.

Desviaciones del comportamiento ideal de los gases reales

La ecuación de estado dada aquí (PV = nRT) se aplica solo a un gas ideal, o como una aproximación a un gas real que se comporta suficientemente como un gas ideal. De hecho, hay muchas formas diferentes de la ecuación de estado. Dado que la ley de los gases ideales ignora tanto el tamaño molecular como las atracciones intermoleculares, es más precisa para gases monoatómicos a altas temperaturas y bajas presiones. El descuido del tamaño molecular se vuelve menos importante para densidades más bajas, es decir, para volúmenes más grandes a presiones más bajas, porque la distancia promedio entre moléculas adyacentes se vuelve mucho mayor que el tamaño molecular. La importancia relativa de las atracciones intermoleculares disminuye al aumentar la energía cinética térmica, es decir, al aumentar la temperatura. Las ecuaciones de estado más detalladas, como la ecuación de van der Waals, explican las desviaciones de la idealidad causadas por el tamaño molecular y las fuerzas intermoleculares.

Derivaciones

Empírico

Las leyes empíricas que llevaron a la derivación de la ley de los gases ideales se descubrieron con experimentos que cambiaron solo 2 variables de estado del gas y mantuvieron constantes todas las demás.

Todas las posibles leyes de los gases que podrían haberse descubierto con este tipo de configuración son:

La ley de BoyleEcuación 1) ${displaystyle PV=C_{1}quad {text{or}}quad P_{1}V_{1}=P_{2}V_{2}}$
Ley de CharlesEcuación 2) ${displaystyle {frac {V}{T}}=C_{2}quad {text{or}}quad {frac {V_{1}}{T_{1}}}={frac {V_{2}}{T_{2}}}}$
Ley de AvogadroEcuación 3) ${displaystyle {frac {V}{N}}=C_{3}quad {text{or}}quad {frac {V_{1}}{N_{1}}}={frac {V_{2}}{N_{2}}}}$
Ley de Gay-LussacEcuación 4) ${displaystyle {frac {P}{T}}=C_{4}quad {text{or}}quad {frac {P_{1}}{T_{1}}}={frac {P_{2}}{T_{2}}}}$
Ecuación 5 ${displaystyle NT=C_{5}quad {text{or}}quad N_{1}T_{1}=N_{2}T_{2}}$
Ecuación 6 ${displaystyle {frac {P}{N}}=C_{6}quad {text{or}}quad {frac {P_{1}}{N_{1}}}={frac {P_{2}}{N_{2}}}}$

Relaciones entre Boyle's, Charles's, Gay-Lussac's, Avogadro's, combinadas y leyes de gas ideales, con la constante de Boltzmann k_B = RN_A = RN (en cada ley, las propiedades circunscritas son variables y las propiedades no circuncidadas se mantienen constantes)

Donde P significa presión, V para volumen, N para el número de partículas en el gas y T para la temperatura; donde ${displaystyle C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}}$ son constantes en este contexto debido a cada ecuación que requiere sólo los parámetros explícitamente señalados en ellos cambiando.

Para derivar la ley de los gases ideales, no es necesario conocer las 6 fórmulas, solo se pueden conocer 3 y con ellas derivar el resto o solo una más para poder obtener la ley de los gases ideales, que necesita 4.

Dado que cada fórmula solo se cumple cuando solo las variables de estado involucradas en dicha fórmula cambian mientras que las otras (que son una propiedad del gas pero no se indican explícitamente en dicha fórmula) permanecen constantes, no podemos simplemente usar el álgebra y combinarlas directamente. todas. Esta es la razón: Boyle hizo sus experimentos manteniendo constantes N y T y esto hay que tenerlo en cuenta (de la misma manera, cada experimento mantuvo algún parámetro como constante y esto debe tenerse en cuenta para la derivación).

Teniendo esto en cuenta, para llevar a cabo la derivación correctamente, uno debe imaginar que el gas es alterado por un proceso a la vez (como se hizo en los experimentos). La derivación usando 4 fórmulas puede verse así:

al principio el gas tiene parámetros ${displaystyle P_{1},V_{1},N_{1},T_{1}}$

Diga, comenzando a cambiar solo la presión y el volumen, de acuerdo con la ley de Boyle (Ecuación 1), entonces:

{displaystyle P_{1}V_{1}=P_{2}V_{2}}

()7)

Después de este proceso, el gas tiene parámetros ${displaystyle P_{2},V_{2},N_{1},T_{1}}$

Usando la ecuación (5) para cambiar el número de partículas en el gas y la temperatura,

{displaystyle N_{1}T_{1}=N_{2}T_{2}}

()8)

Después de este proceso, el gas tiene parámetros ${displaystyle P_{2},V_{2},N_{2},T_{2}}$

Usando la ecuación (6) para cambiar la presión y el número de partículas,

{displaystyle {frac {P_{2}}{N_{2}}}={frac {P_{3}}{N_{3}}}}

()9)

Después de este proceso, el gas tiene parámetros ${displaystyle P_{3},V_{2},N_{3},T_{2}}$

Usando la ley de Charles (ecuación 2) para cambiar el volumen y la temperatura del gas,

{displaystyle {frac {V_{2}}{T_{2}}}={frac {V_{3}}{T_{3}}}}

()10)

Después de este proceso, el gas tiene parámetros ${displaystyle P_{3},V_{3},N_{3},T_{3}}$

Usando álgebra simple en ecuaciones (7), (8), (9) y (10) da el resultado:

{displaystyle {frac {P_{1}V_{1}}{N_{1}T_{1}}}={frac {P_{3}V_{3}}{N_{3}T_{3}}}}

{displaystyle {frac {PV}{NT}}=k_{text{B}},}

{displaystyle k_{text{B}}}

Otro resultado equivalente, utilizando el hecho de que ${displaystyle nR=Nk_{text{B}}}$ , donde n es el número de lunares en el gas y R es la constante del gas universal, es:

{displaystyle PV=nRT,}

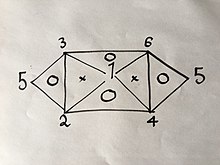
Si se conocen tres de las seis ecuaciones, es posible derivar las tres restantes usando el mismo método. Sin embargo, debido a que cada fórmula tiene dos variables, esto solo es posible para ciertos grupos de tres. Por ejemplo, si tuviera ecuaciones (1), (2) y (4) no podría obtener más porque combinar dos de ellos solo te dará el tercero. Sin embargo, si tuviera las ecuaciones (1), (2) y (3) podría obtener las seis ecuaciones porque al combinar (1) y (2) producirán (4), luego (1) y (3 ) producirá (6), luego (4) y (6) producirá (5), así como sería la combinación de (2) y (3) como se explica en la siguiente relación visual:

Relación entre las seis leyes de gas

donde los números representan las leyes de los gases numeradas arriba.

Si usara el mismo método que se usó anteriormente en 2 de las 3 leyes sobre los vértices de un triángulo que tiene una "O" dentro de él, obtendrías el tercero.

Por ejemplo:

Cambia solo la presión y el volumen primero:

{displaystyle P_{1}V_{1}=P_{2}V_{2}}

()1 ')

entonces solo volumen y temperatura:

{displaystyle {frac {V_{2}}{T_{1}}}={frac {V_{3}}{T_{2}}}}

()2 ')

entonces como podemos elegir cualquier valor para $V_{3}$ , si nos fijamos ${displaystyle V_{1}=V_{3}}$ , ecuación2 ') se convierte en:

{displaystyle {frac {V_{2}}{T_{1}}}={frac {V_{1}}{T_{2}}}}

()3 ')

combinación de ecuaciones (1 ') y (3 ') rendimientos ${displaystyle {frac {P_{1}}{T_{1}}}={frac {P_{2}}{T_{2}}}}$ , que es la ecuación (4), de los cuales no teníamos conocimiento previo hasta esta derivación.

Teórico

Teoría cinética

La ley de los gases ideales también se puede derivar de los primeros principios utilizando la teoría cinética de los gases, en la que se hacen varias suposiciones simplificadas, entre las que destaca que las moléculas, o átomos, del gas son masas puntuales, que poseen masa pero no tienen un volumen significativo y solo sufren colisiones elásticas entre sí y con los lados del recipiente en el que se conservan tanto el momento lineal como la energía cinética.

Los supuestos fundamentales de la teoría cinética de los gases implican que

{displaystyle PV={frac {1}{3}}Nmv_{text{rms}}^{2}.}

Usando la distribución Maxwell-Boltzmann, la fracción de moléculas que tienen una velocidad en el rango $v$ a ${displaystyle v+dv}$ es ${displaystyle f(v),dv}$ , donde

{displaystyle f(v)=4pi left({frac {m}{2pi kT}}right)^{!{frac {3}{2}}}v^{2}e^{-{frac {mv^{2}}{2kT}}}}

y $k$ denota la constante Boltzmann. La velocidad del cuadrado de raíz puede calcularse por

{displaystyle v_{text{rms}}^{2}=int _{0}^{infty }v^{2}f(v),dv=4pi left({frac {m}{2pi kT}}right)^{frac {3}{2}}int _{0}^{infty }v^{4}e^{-{frac {mv^{2}}{2kT}}},dv.}

Uso de la fórmula de integración

{displaystyle int _{0}^{infty }x^{2n}e^{-{frac {x^{2}}{a^{2}}}},dx={sqrt {pi }},{frac {(2n)!}{n!}}left({frac {a}{2}}right)^{2n+1},}

se deduce que

{displaystyle v_{text{rms}}^{2}=4pi left({frac {m}{2pi kT}}right)^{!{frac {3}{2}}}{sqrt {pi }},{frac {4!}{2!}}left({frac {sqrt {frac {2kT}{m}}}{2}}right)^{!5}={frac {3kT}{m}},}

de donde obtenemos la ley de los gases ideales:

{displaystyle PV={frac {1}{3}}Nmleft({frac {3kT}{m}}right)=NkT.}

Mecánica estadística

Sea q = (q_x, q_y, q_z) y p = (p_x, p_y, p_z) denotan el vector de posición y el vector de momento de una partícula de un gas ideal, respectivamente. Sea F la fuerza neta sobre esa partícula. Entonces la energía cinética promediada en el tiempo de la partícula es:

{displaystyle {begin{aligned}langle mathbf {q} cdot mathbf {F} rangle &=leftlangle q_{x}{frac {dp_{x}}{dt}}rightrangle +leftlangle q_{y}{frac {dp_{y}}{dt}}rightrangle +leftlangle q_{z}{frac {dp_{z}}{dt}}rightrangle \&=-leftlangle q_{x}{frac {partial H}{partial q_{x}}}rightrangle -leftlangle q_{y}{frac {partial H}{partial q_{y}}}rightrangle -leftlangle q_{z}{frac {partial H}{partial q_{z}}}rightrangle =-3k_{text{B}}T,end{aligned}}}

donde la primera igualdad es la segunda ley de Newton y la segunda línea usa las ecuaciones de Hamilton y el teorema de equipartición. Sumando sobre un sistema de N rendimientos de partículas

{displaystyle 3Nk_{B}T=-leftlangle sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}rightrangle.}

Por la tercera ley de Newton y el supuesto del gas ideal, la fuerza neta del sistema es la fuerza aplicada por las paredes del recipiente, y esta fuerza viene dada por la presión P del gas Por lo tanto

{displaystyle -leftlangle sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}rightrangle =Point _{text{surface}}mathbf {q} cdot dmathbf {S}}

donde dS es el elemento de área infinitesimal a lo largo de las paredes del contenedor. Dado que la divergencia del vector de posición q es

nabla cdot mathbf {q} ={frac {partial q_{x}}{partial q_{x}}}+{frac {partial q_{y}}{partial q_{y}}}+{frac {partial q_{z}}{partial q_{z}}}=3,

el teorema de la divergencia implica que

{displaystyle Point _{text{surface}}mathbf {q} cdot dmathbf {S} =Pint _{text{volume}}left(nabla cdot mathbf {q} right)dV=3PV,}

donde dV es un volumen infinitesimal dentro del contenedor y V es el volumen total del contenedor.

Juntando estas igualdades se obtiene

{displaystyle 3Nk_{text{B}}T=-leftlangle sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}rightrangle =3PV,}

lo que implica inmediatamente la ley de los gases ideales para N partículas:

{displaystyle PV=Nk_{B}T=nRT,}

donde n = N/N_A es el número de moles de gas y R = N_Ak_B es la constante de los gases.

Otras dimensiones

Para un sistema d-dimensional, la presión de gas ideal es:

{displaystyle P^{(d)}={frac {Nk_{B}T}{L^{d}}},}

Donde ${displaystyle L^{d}}$ es el volumen del d- dominio dimensional en el que existe el gas. Tenga en cuenta que las dimensiones de la presión cambian con dimensionalidad.

Contenido relacionado

Más resultados...