Ley de kleiber

ley de Kleiber, llamada así en honor a Max Kleiber por su trabajo en biología a principios de la década de 1930, es la observación de que, para la gran mayoría de los animales, la tasa metabólica de un animal escala al 3⁄4 potencia del animal masa. Más recientemente, también se ha demostrado que la ley de Kleiber se aplica a las plantas, lo que sugiere que la observación de Kleiber es mucho más general. Simbólicamente: si B es la tasa metabólica del animal y M es la masa del animal, entonces la ley de Kleiber establece que B~M^3/4. Así, en el mismo lapso de tiempo, un gato que tenga una masa 100 veces mayor que la de un ratón consumirá sólo unas 32 veces la energía que utiliza el ratón.

El valor exacto del exponente en la ley de Kleiber no está claro, en parte porque la ley actualmente carece de una única explicación teórica que sea completamente satisfactoria.

Explicaciones propuestas para la ley

La ley de Kleiber, como muchas otras leyes alométricas biológicas, es una consecuencia de la física y/o geometría de los sistemas circulatorios en biología. Max Kleiber descubrió la ley por primera vez al analizar una gran cantidad de estudios independientes sobre la respiración dentro de especies individuales. Kleiber esperaba encontrar un exponente de 2⁄3 (por razones explicadas a continuación), y quedó confundido por el descubrimiento de un 3⁄4 exponente.

Contexto histórico y la ley de superficie de escala de 2⁄3

Antes de que Kleiber observara la escala de potencia de 3/4, se anticipaba en gran medida una escala de potencia de 2/3 basándose en la "ley de la superficie", que establece que el metabolismo basal de animales que difieren en El tamaño es casi proporcional a sus respectivas superficies corporales. Este razonamiento de la ley de superficie se originó a partir de consideraciones geométricas simples. A medida que los organismos aumentan de tamaño, su volumen (y por tanto su masa) aumenta a un ritmo mucho más rápido que su superficie. Las explicaciones para el escalamiento 2⁄3 tienden a suponer que las tasas metabólicas aumentan para evitar el agotamiento por calor. Debido a que los cuerpos pierden calor pasivamente a través de su superficie pero producen calor metabólicamente en toda su masa, la tasa metabólica debe escalar de tal manera que contrarreste la ley del cuadrado-cubo. Debido a que se creía que muchos procesos fisiológicos, como la pérdida de calor y la absorción de nutrientes, dependían de la superficie de un organismo, se planteó la hipótesis de que la tasa metabólica aumentaría con 2/3 de la masa corporal. Rubner (1883) demostró por primera vez la ley en pruebas de respiración precisa en perros.

La contribución de Kleiber

Max Kleiber cuestionó esta noción a principios de la década de 1930. A través de una extensa investigación sobre varios animales' tasas metabólicas, encontró que una escala de potencia de 3/4 proporcionaba un mejor ajuste a los datos empíricos que la potencia de 2/3. Sus hallazgos sentaron las bases para comprender las leyes de escala alométrica en biología, lo que llevó a la formulación de la teoría de escala metabólica y al trabajo posterior de West, Brown y Enquist, entre otros.

Tal argumento no aborda el hecho de que diferentes organismos exhiben diferentes formas (y por lo tanto tienen diferentes relaciones superficie-volumen, incluso cuando se escalan al mismo tamaño). Estimaciones razonables para los organismos' El área de superficie parece aumentar linealmente con la tasa metabólica.

Exponente 3⁄4

West, Brown y Enquist (en adelante WBE) propusieron una teoría general para el origen de muchas leyes de escala alométrica en biología. Según la teoría WBE, el escalamiento 3⁄4 surge debido a Eficiencia en la distribución y transporte de nutrientes a través de un organismo. En la mayoría de los organismos, el metabolismo está respaldado por un sistema circulatorio con túbulos ramificados (es decir, sistemas vasculares de plantas, tráqueas de insectos o el sistema cardiovascular humano). WEB afirma que (1) el metabolismo debe escalar proporcionalmente al flujo de nutrientes (o, equivalentemente, al flujo total de fluidos) en este sistema circulatorio y (2) para minimizar la energía disipada en el transporte, el volumen de fluido utilizado para transportar nutrientes (es decir, , volumen sanguíneo) es una fracción fija de la masa corporal.

A continuación, analizan las consecuencias de estas dos afirmaciones a nivel de los túbulos circulatorios más pequeños (capilares, alvéolos, etc.). Experimentalmente, el volumen contenido en esos túbulos más pequeños es constante en una amplia gama de masas. Debido a que el flujo de fluido a través de un túbulo está determinado por su volumen, el flujo de fluido total es proporcional al número total de túbulos más pequeños. Por lo tanto, si B denota la tasa metabólica basal, Q el flujo total de fluido y N el número de túbulos mínimos,

$${\displaystyle B\propto Q\propto N{\text{}}$$

$${\displaystyle N^{4}\propto V^{3}{\text{}}$$

$${\displaystyle B\propto M^{\frac {3} {4} {\text{}}}}$$

Escalado sin ley de potencia

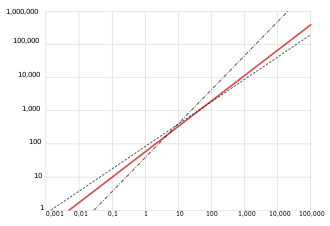
Un análisis más detallado sugiere que la ley de Kleiber puede variar dentro y entre especies. Las tasas metabólicas de animales más pequeños (aves de menos de 10 kg [22 lb] o insectos) normalmente se ajustan a 2⁄3 mucho mejor que 3⁄4; para animales más grandes ocurre lo contrario. Como resultado, las gráficas log-log de la tasa metabólica versus la masa corporal parecen "curvar" la proporción. hacia arriba y se ajustan mejor a los modelos cuadráticos. En todos los casos, los ajustes locales exhiben exponentes en el [2⁄3 ,3⁄4]< /span> rango.

Modelos circulatorios modificados

Los ajustes al modelo WBE que mantienen supuestos sobre la forma de la red predicen exponentes de escala más grandes, lo que empeora la discrepancia con los datos observados. Pero se puede mantener una teoría similar relajando el supuesto de WBE de una red de transporte de nutrientes que es a la vez fractal y circulatoria. Las diferentes redes son menos eficientes porque exhiben un exponente de escala más bajo, pero una tasa metabólica determinada por el transporte de nutrientes siempre exhibirá una escala entre 2⁄ 3 y 3⁄4< /span>. (WBE argumentó que las redes circulatorias fractales necesariamente evolucionarían para minimizar la energía utilizada para el transporte, pero otros investigadores argumentan que su derivación contiene errores sutiles). Si evolutivamente se favorecen tasas metabólicas más altas, entonces los organismos de baja masa preferirán organizar sus redes a escala. como 2⁄3, pero los organismos de gran masa preferirán organizar sus redes como 3⁄4, lo que produce la curvatura observada.

Modelos termodinámicos modificados

Un modelo alternativo señala que la tasa metabólica no solo sirve para generar calor. La tasa metabólica que contribuye exclusivamente al trabajo útil debe escalar con potencia 1 (en línea), mientras que la tasa metabólica que contribuye a la generación de calor debe limitarse por superficie y escala con potencia 2.3. La tasa metabólica basal es entonces la combinación convexa de estos dos efectos: si la proporción de trabajo útil es f, entonces la tasa metabólica basal debe escalar

$${\displaystyle B=f\cdot kM+(1-f)\cdot k'M^{\frac {2}{3}}$$

Crítica de las explicaciones

Kozłowski y Konarzewski han argumentado que los intentos de explicar la ley de Kleiber mediante cualquier tipo de factor limitante son erróneos, porque las tasas metabólicas varían en factores de 4 a 5 entre el reposo y la actividad. Por lo tanto, cualquier límite que afecte la escala de la tasa metabólica basal haría de hecho imposible un metabolismo elevado (y, por tanto, toda actividad animal). WBE, por el contrario, sostiene que los animales pueden optimizar la disipación mínima de energía del transporte durante el descanso, sin abandonar la capacidad de realizar funciones menos eficientes en otros momentos.

Otros investigadores también han observado que las críticas de Kozłowski y Konarzewski a la ley tienden a centrarse en detalles estructurales precisos de las redes circulatorias de WBE, pero que estas últimas no son esenciales para el modelo.

Soporte experimental

Los análisis de varianza para una variedad de variables físicas sugieren que, aunque la mayor variación en la tasa metabólica basal está determinada por la masa, variables adicionales con efectos significativos incluyen la temperatura corporal y el orden taxonómico.

Un trabajo de Brody de 1932 calculó que la escala era aproximadamente 0,73.

Un análisis de 2004 de las tasas metabólicas de campo de los mamíferos concluye que parecen escalar con un exponente de 0,749.

Generalizaciones

Se ha informado de la ley de Kleiber en comparaciones interespecíficas y se ha afirmado que no se aplica a nivel intraespecífico. Se ha debatido el nivel taxonómico en el que se debe estudiar la alometría metabólica de la masa corporal. No obstante, varios análisis sugieren que, si bien los exponentes de la relación de Kleiber entre el tamaño corporal y el metabolismo pueden variar a nivel intraespecífico, estadísticamente, los exponentes intraespecíficos tanto en plantas como en animales tienden a agruparse alrededor de 3/4.

En otros reinos

Un análisis de 1999 concluyó que la producción de biomasa en una planta determinada se escalaba con el 3⁄4 poder de la masa de la planta durante su crecimiento, pero un artículo de 2001 que incluía varios tipos de organismos fotosintéticos unicelulares encontró exponentes de escala intermedios entre 0,75 y 1,00.

Un artículo de 2006 en Nature argumentó que el exponente de masa es cercano a 1 para las plántulas de plantas, pero que la variación entre especies, filos y condiciones de crecimiento abruma cualquier análisis "Kleiber' s efectos similares a los de una ley.

Resultados intraorganismos

Debido a que el protoplasma celular parece tener una densidad constante en una variedad de masas de organismos, una consecuencia de la ley de Kleiber es que, en especies más grandes, hay menos energía disponible para cada volumen celular. Las células parecen hacer frente a esta dificultad eligiendo una de las dos estrategias siguientes: células más pequeñas o una tasa metabólica celular más lenta. Las neuronas y los adipocitos presentan lo primero; cualquier otro tipo de célula, este último. Como resultado, diferentes órganos exhiben diferentes escalas alométricas (ver tabla).

Escaladas alométricas para BMR-vs.-masa en tejido humano

Organ	Scaling exponent
Cerebro	0.7
Kidney	0.85
Liver	0.87
Corazón	0.98
Musculo	1.0
Skeleton	1.1