Ley de inducción de Faraday

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Derecho básico de electromagnetismo

La ley de inducción de Faraday (o simplemente ley de Faraday) es una ley del electromagnetismo que predice cómo interactuará un campo magnético con una energía eléctrica. circuito para producir una fuerza electromotriz (fem). Este fenómeno, conocido como inducción electromagnética, es el principio de funcionamiento fundamental de transformadores, inductores y muchos tipos de motores, generadores y solenoides eléctricos.

La ecuación de Maxwell-Faraday (incluida como una de las ecuaciones de Maxwell) describe el hecho de que un campo magnético que varía espacialmente (y también posiblemente que varía en el tiempo, dependiendo de cómo varía un campo magnético) tiempo) el campo eléctrico siempre acompaña a un campo magnético variable en el tiempo, mientras que la ley de Faraday establece que hay fem (fuerza electromotriz, definida como el trabajo electromagnético realizado sobre una unidad de carga cuando ha recorrido una vuelta de un bucle conductor) en un bucle conductor cuando el flujo magnético a través de la superficie encerrada por el bucle varía en el tiempo.

La ley de Faraday había sido descubierta y un aspecto de ella (la fem del transformador) se formuló más tarde como la ecuación de Maxwell-Faraday. La ecuación de la ley de Faraday se puede derivar mediante la ecuación de Maxwell-Faraday (que describe la fem del transformador) y la fuerza de Lorentz (que describe la fem del movimiento). La forma integral de la ecuación de Maxwell-Faraday describe sólo la fem del transformador, mientras que la ecuación de la ley de Faraday describe tanto la fem del transformador como la fem del movimiento.

Historia

La inducción electromagnética fue descubierta de forma independiente por Michael Faraday en 1831 y Joseph Henry en 1832. Faraday fue el primero en publicar los resultados de sus experimentos.

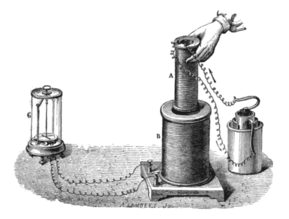
El cuaderno de Faraday el 29 de agosto de 1831 describe una demostración experimental de inducción electromagnética (ver figura) que envuelve dos alambres alrededor de los lados opuestos de un anillo de hierro (como un transformador toroidal moderno). Su evaluación de propiedades recién descubiertas de electromagnets sugirió que cuando la corriente comenzó a fluir en un alambre, una especie de ola viajaría a través del anillo y causaría algún efecto eléctrico en el lado opuesto. De hecho, la aguja de un galvanometer midió una corriente transitoria (que él llamó una "onda de electricidad") en el alambre del lado derecho cuando se conectaba o desconectó el cable del lado izquierdo a una batería. Esta inducción se debió al cambio de flujo magnético que ocurrió cuando la batería estaba conectada y desconectada. Su entrada de cuaderno también señaló que menos envolturas para el lado de la batería resultaron en una mayor perturbación de la aguja del galvanometer.

En dos meses, Faraday había encontrado varias otras manifestaciones de inducción electromagnética. Por ejemplo, vio corrientes transitorias cuando rápidamente deslizó una barra magnética dentro y fuera de una bobina de cables, y generó una corriente constante (CC) al girar un disco de cobre cerca de la barra magnética con un cable eléctrico deslizante (&#34 ;Disco de Faraday").

Michael Faraday explicó la inducción electromagnética utilizando un concepto que llamó líneas de fuerza. Sin embargo, los científicos de la época rechazaron ampliamente sus ideas teóricas, principalmente porque no estaban formuladas matemáticamente. Una excepción fue James Clerk Maxwell, quien en 1861-1862 utilizó las ideas de Faraday como base de su teoría electromagnética cuantitativa. En los artículos de Maxwell, el aspecto de la inducción electromagnética que varía en el tiempo se expresa como una ecuación diferencial a la que Oliver Heaviside denominó ley de Faraday, aunque es diferente de la versión original de la ley de Faraday. , y no describe la fem en movimiento. La versión de Heaviside (consulte la ecuación de Maxwell-Faraday a continuación) es la forma reconocida hoy en el grupo de ecuaciones conocidas como ecuaciones de Maxwell.

La ley de Lenz, formulada por Emil Lenz en 1834, describe el "flujo a través del circuito" y proporciona la dirección de la fem inducida y la corriente resultante de la inducción electromagnética (elaborada en los ejemplos abajo).

Según Albert Einstein, gran parte del trabajo preliminar y descubrimiento de su teoría de la relatividad especial fue presentado por esta ley de inducción por Faraday en 1834.

Ley de Faraday

La versión más extendida de la ley de Faraday establece:

La fuerza electromotiva alrededor de un camino cerrado es igual al negativo de la velocidad de cambio del flujo magnético encerrado por el camino.

Declaración matemática

Para un bucle de alambre en un campo magnético, el flujo magnético $CCPR B$ se define para cualquier superficie $.$ cuyo límite es el bucle dado. Como el bucle de alambre puede estar en movimiento, escribimos $(Risas) t)$ para la superficie. El flujo magnético es la superficie integral:

{displaystyle Phi _{B}=iint _{Sigma (t)}mathbf {B} (t)cdot mathrm {d} mathbf {A} ,,}

d A

(Risas) t)

B

B \cdot d A

d A

Cuando el flujo cambia, porque $B$ cambia, o porque el bucle de alambre se mueve o se deforma, o ambas cosas, se aplica la ley de Faraday. La inducción dice que el bucle de alambre adquiere una fem, definida como la energía disponible de una unidad de carga que ha viajado una vez alrededor del bucle de alambre. (Aunque algunas fuentes establecen la definición de manera diferente, esta expresión se eligió por compatibilidad con las ecuaciones de la relatividad especial). De manera equivalente, es el voltaje que se mediría cortando el cable para crear un circuito abierto y conectando un voltímetro a los cables. .

La ley de Faraday establece que la fem también viene dada por la tasa de cambio del flujo magnético:

{displaystyle {mathcal {E}}=-{frac {mathrm {d} Phi _{B}}{mathrm {d} t}},}

{displaystyle {mathcal {E}}}

CCPR B

La dirección de la fuerza electromotiva es dada por la ley de Lenz.

Las leyes de inducción de corrientes eléctricas en forma matemática fueron establecidas por Franz Ernst Neumann en 1845.

La ley de Faraday contiene información sobre las relaciones entre las magnitudes y las direcciones de sus variables. Sin embargo, las relaciones entre las direcciones no son explícitas; están ocultos en la fórmula matemática.

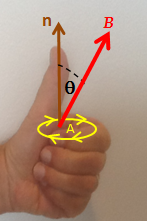
Una regla de mano izquierda para la ley de Faraday. El signo de $Δ Negotiat B$ , el cambio de flujo, se encuentra basado en la relación entre el campo magnético $B$ , el área del bucle $A$ , y la n normal a esa zona, representada por los dedos de la mano izquierda. Si $Δ Negotiat B$ es positivo, la dirección del emf es la misma que la de los dedos curvados (cabezas amarillas). Si $Δ Negotiat B$ es negativo, la dirección del emf está contra las puntas de flecha.

Es posible descubrir la dirección de la fuerza electromotriz (fem) directamente a partir de la ley de Faraday, sin invocar la ley de Lenz. Una regla de la mano izquierda ayuda a hacer esto, de la siguiente manera:

Alinear los dedos curvados de la mano izquierda con el bucle (línea amarilla).
Aprieta el pulgar. El pulgar estirado indica la dirección $n$ (brown), lo normal a la zona encerrada por el bucle.
Encontrar el signo de $Δ Negotiat B$ El cambio de flujo. Determinar los flujos iniciales y finales (cuya diferencia es $Δ Negotiat B$ ) con respecto a lo normal $n$ , como se indica en el pulgar estirado.
Si el cambio en el flujo, $Δ Negotiat B$ , es positivo, los dedos curvados muestran la dirección de la fuerza electromotiva (cabezas de flecha amarillas).
Si $Δ Negotiat B$ es negativo, la dirección de la fuerza electromotiva es opuesta a la dirección de los dedos curvados (opuesta a las puntas de flecha amarillas).

Para una bobina de alambre bien enrollada, compuesta de $N$ vueltas idénticas, cada una con el mismo $Φ B$ , la ley de inducción de Faraday establece que

{displaystyle {mathcal {E}}=-N{frac {mathrm {d} Phi _{B}}{mathrm {d} t}}}

N

CCPR B

Ecuación de Maxwell-Faraday

La ecuación de Maxwell-Faraday establece que un campo magnético variable en el tiempo siempre acompaña a un campo eléctrico no conservativo que varía espacialmente (también posiblemente que varía en el tiempo), y viceversa. La ecuación de Maxwell-Faraday es

${displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} }{partial t}}}$

(en unidades SI) donde $\nabla \times$ es el operador de curvatura y nuevamente $E (r, t)$ es el campo eléctrico y $B (r, t)$ es el campo magnético. Estos campos generalmente pueden ser funciones de posición $r$ y tiempo $t$ .

La ecuación de Maxwell-Faraday es una de las cuatro ecuaciones de Maxwell y, por tanto, juega un papel fundamental en la teoría del electromagnetismo clásico. También se puede escribir en forma integral mediante el teorema de Kelvin-Stokes, reproduciendo así la ley de Faraday:

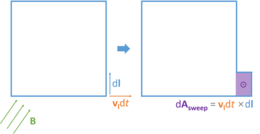
${displaystyle oint _{partial Sigma }mathbf {E} cdot mathrm {d} mathbf {l} =-int _{Sigma }{frac {partial mathbf {B} }{partial t}}cdot mathrm {d} mathbf {A} }$

donde, como se indica en la figura, $Σ$ es una superficie delimitada por el contorno cerrado $\partial Σ$ , $d l$ es un elemento vectorial infinitesimal del contorno $\partialΣ$ , y $d A$ es un elemento vectorial infinitesimal de superficie $Σ$ . Su dirección es ortogonal a ese parche de superficie, la magnitud es el área de un parche de superficie infinitesimal.

Tanto $d l$ como $d A$ tienen un signo ambigüedad; para obtener el signo correcto se utiliza la regla de la mano derecha, como se explica en el artículo Teorema de Kelvin-Stokes. Para una superficie plana $Σ$ , un elemento de trayectoria positiva $d l$ de curva $\partial Σ$ se define por la regla de la mano derecha como aquella que apunta con los dedos de la mano derecha cuando el pulgar apunta en la dirección de la normal $n$ a la superficie $Σ$ .

La integral de línea alrededor de $\partial Σ$ se llama circulación. Una circulación distinta de cero de $E$ es diferente del comportamiento del campo eléctrico generado por cargas estáticas. Un campo $E$ generado por carga se puede expresar como el gradiente de un campo escalar que es una solución a la ecuación de Poisson y tiene una integral de trayectoria cero. Ver teorema del gradiente.

La ecuación integral es verdadera para cualquier camino $\partial Σ$ a través del espacio y cualquier superficie $Σ$ para el cual ese camino es un límite.

Si la superficie $Σ$ no cambia con el tiempo, la ecuación se puede reescribir:

{displaystyle oint _{partial Sigma }mathbf {E} cdot mathrm {d} mathbf {l} =-{frac {mathrm {d} }{mathrm {d} t}}int _{Sigma }mathbf {B} cdot mathrm {d} mathbf {A}.}

CCPR B

.

El campo vectorial eléctrico inducido por un flujo magnético cambiante, el componente solenoidal del campo eléctrico general, puede aproximarse en el límite no relativista mediante la ecuación integral de volumen

{displaystyle mathbf {E} _{s}(mathbf {r}t)approx -{frac {1}{4pi }}iiint _{V} {frac {left({frac {partial mathbf {B} (mathbf {r} ',t)}{partial t}}right)times left(mathbf {r} -mathbf {r} 'right)}{|mathbf {r} -mathbf {r} '|^{3}}}d^{3}mathbf {r'} }

Prueba

Las cuatro ecuaciones de Maxwell (incluida la ecuación de Maxwell-Faraday), junto con la ley de fuerza de Lorentz, son una base suficiente para derivar todo en el electromagnetismo clásico. Por tanto, es posible "probar" La ley de Faraday a partir de estas ecuaciones.

El punto de partida es el tiempo-derivativo del flujo a través de una superficie arbitraria $.$ (que se puede mover o deformar) en el espacio:

{displaystyle {frac {mathrm {d} Phi _{B}}{mathrm {d} t}}={frac {mathrm {d} }{mathrm {d} t}}int _{Sigma (t)}mathbf {B} (t)cdot mathrm {d} mathbf {A} }

(por definición). Esta derivada del tiempo total se puede evaluar y simplificar con la ayuda de la ecuación de Maxwell-Faraday y algunas identidades vectoriales; los detalles están en el cuadro a continuación:

Considere el tiempo-derivativo del flujo magnético a través de un límite cerrado (op) que puede moverse o ser deformado. El área atada por el bucle se denota como $(Risas) t)$ ), entonces el tiempo-derivativo se puede expresar como ${displaystyle {frac {mathrm {d} Phi _{B}}{mathrm {d} t}}={frac {mathrm {d} }{mathrm {d} t}}int _{Sigma (t)}mathbf {B} (t)cdot mathrm {d} mathbf {A} }$ La integral puede cambiar con el tiempo por dos razones: El integrado puede cambiar, o la región de integración puede cambiar. Por lo tanto, éstos agregan linealmente: ${displaystyle left.{frac {mathrm {d} Phi _{B}}{mathrm {d} t}}right\|_{t=t_{0}}=left(int _{Sigma (t_{0})}left.{frac {partial mathbf {B} }{partial t}}right\|_{t=t_{0}}cdot mathrm {d} mathbf {A} right)+left({frac {mathrm {d} }{mathrm {d} t}}int _{Sigma (t)}mathbf {B} (t_{0})cdot mathrm {d} mathbf {A} right)}$ Donde $t 0$ es un tiempo fijo dado. Demostraremos que el primer término en el lado derecho corresponde al transformador emf, el segundo al emf de movimiento (de la fuerza magnética Lorentz en los transportistas de carga debido al movimiento o deformación del bucle de conducción en el campo magnético). El primer término en el lado derecho puede ser reescrito utilizando la forma integral de la ecuación Maxwell-Faraday: ${displaystyle int _{Sigma (t_{0})}left.{frac {partial mathbf {B} }{partial t}}right\|_{t=t_{0}}cdot mathrm {d} mathbf {A} =-oint _{partial Sigma (t_{0})}mathbf {E} (t_{0})cdot mathrm {d} mathbf {l} }$ A continuación, analizamos el segundo término en el lado derecho: ${displaystyle {frac {mathrm {d} }{mathrm {d} t}}int _{Sigma (t)}mathbf {B} (t_{0})cdot mathrm {d} mathbf {A} }$ El área es barrida por un elemento vectorial $d l$ de un bucle $\partial .$ en el tiempo $d t$ cuando se ha movido con velocidad $v l$ . La prueba de esto es un poco más difícil que el primer término; más detalles y enfoques alternativos para la prueba se pueden encontrar en las referencias. A medida que el bucle se mueve y/o deforma, barre una superficie (ver la figura correcta). Como una pequeña parte del bucle $d l$ movimientos con velocidad $v l$ en un corto tiempo $d t$ , barre un área cuyo vector es $d A barrido barrido = v l d t \times l$ (nota que este vector está hacia fuera de la pantalla en la figura correcta). Por lo tanto, el cambio del flujo magnético a través del bucle debido a la deformación o movimiento del bucle a lo largo del tiempo $d t$ es ${displaystyle mathrm {d} Phi _{B}=int mathbf {B} cdot mathrm {d} mathbf {A} _{text{sweep}}=int mathbf {B} cdot (mathbf {v} _{mathbf {l} }mathrm {d} ttimes mathrm {d} mathbf {l})=-int mathrm {d} t,mathrm {d} mathbf {l} cdot (mathbf {v} _{mathbf {l} }times mathbf {B})}$ Aquí se utilizan las identidades de los productos de triple escalar. Por lo tanto, ${displaystyle {frac {mathrm {d} }{mathrm {d} t}}int _{Sigma (t)}mathbf {B} (t_{0})cdot mathrm {d} mathbf {A} =-oint _{partial Sigma (t_{0})}(mathbf {v} _{mathbf {l} }(t_{0})times mathbf {B} (t_{0}))cdot mathrm {d} mathbf {l} }$ Donde $v l$ es la velocidad de una parte del bucle $\partial .$ . Poner estos resultados juntos en, ${displaystyle left.{frac {mathrm {d} Phi _{B}}{mathrm {d} t}}right\|_{t=t_{0}}=left(-oint _{partial Sigma (t_{0})}mathbf {E} (t_{0})cdot mathrm {d} mathbf {l} right)+left(-oint _{partial Sigma (t_{0})}{bigl (}mathbf {v} _{mathbf {l} }(t_{0})times mathbf {B} (t_{0}){bigr)}cdot mathrm {d} mathbf {l} right)}$ ${displaystyle left.{frac {mathrm {d} Phi _{B}}{mathrm {d} t}}right\|_{t=t_{0}}=-oint _{partial Sigma (t_{0})}{bigl (}mathbf {E} (t_{0})+mathbf {v} _{mathbf {l} }(t_{0})times mathbf {B} (t_{0}){bigr)}cdot mathrm {d} mathbf {l}.}$

El resultado es:

{displaystyle {frac {mathrm {d} Phi _{B}}{mathrm {d} t}}=-oint _{partial Sigma }left(mathbf {E} +mathbf {v} _{mathbf {l} }times mathbf {B} right)cdot mathrm {d} mathbf {l}.}

\partial

.

v l

En el caso de un bucle conductor, la fem (fuerza electromotriz) es el trabajo electromagnético realizado sobre una unidad de carga cuando ha viajado alrededor del bucle una vez, y este trabajo lo realiza la fuerza de Lorentz. Por lo tanto, la fem se expresa como

{displaystyle {mathcal {E}}=oint left(mathbf {E} +mathbf {v} times mathbf {B} right)cdot mathrm {d} mathbf {l} }

{displaystyle {mathcal {E}}}

v

En una vista macroscópica, para cargos en un segmento del bucle, $v$ consta de dos componentes en promedio; uno es la velocidad de la carga a lo largo del segmento $v t$ , y el otro es la velocidad del segmento $v l$ (el bucle está deformado o movido). $v t$ no contribuye a la labor realizada sobre la carga desde la dirección $v t$ es igual a la dirección ${displaystyle mathrm {d} mathbf {l} }$ . Matemáticamente,

{displaystyle (mathbf {v} times mathbf {B})cdot mathrm {d} mathbf {l} =((mathbf {v} _{t}+mathbf {v} _{l})times mathbf {B})cdot mathrm {d} mathbf {l} =(mathbf {v} _{t}times mathbf {B} +mathbf {v} _{l}times mathbf {B})cdot mathrm {d} mathbf {l} =(mathbf {v} _{l}times mathbf {B})cdot mathrm {d} mathbf {l} }

{displaystyle (mathbf {v} _{t}times mathbf {B})}

{displaystyle mathrm {d} mathbf {l} }

{displaystyle mathbf {v} _{t}}

{displaystyle mathrm {d} mathbf {l} }

{displaystyle {frac {mathrm {d} Phi _{B}}{mathrm {d} t}}=-{mathcal {E}}}

{textstyle {mathcal {E}}=oint left(mathbf {E} +mathbf {v} times mathbf {B} right)cdot mathrm {d} mathbf {l} }

{textstyle oint mathbf {E} cdot mathrm {d} mathbf {l} }

{textstyle oint left(mathbf {v} times mathbf {B} right)cdot mathrm {d} mathbf {l} =oint left(mathbf {v} _{l}times mathbf {B} right)cdot mathrm {d} mathbf {l} }

Excepciones

Es tentador generalizar la ley de Faraday para afirmar: Si $\partialΣ$ es cualquier circuito cerrado arbitrario en el espacio. , entonces la derivada total del flujo magnético en el tiempo a través de $Σ$ es igual a la fem alrededor de $\partialΣ$ . Sin embargo, esta afirmación no siempre es cierta y la razón no se debe simplemente a la razón obvia de que la fem no está definida en el espacio vacío cuando no hay ningún conductor presente. Como se señaló en la sección anterior, no se garantiza que la ley de Faraday funcione a menos que la velocidad de la curva abstracta $\partialΣ$ coincida con la velocidad real del material que conduce la electricidad. Los dos ejemplos ilustrados a continuación muestran que a menudo se obtienen resultados incorrectos cuando el movimiento de $\partialΣ$ se divorcia del movimiento del material.

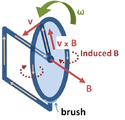
El generador homopolar de Faraday. El disco gira con velocidad angular $\cdot$ , barrendo el radio conductor circularmente en el campo magnético estático $B$ (que dirección es a lo largo de la superficie del disco normal). La fuerza magnética Lorentz $v \times B$ conduce una corriente a lo largo del radio de conducción al borde de conducción, y desde allí el circuito se completa a través del cepillo inferior y el eje que soporta el disco. Este dispositivo genera un emf y una corriente, aunque la forma del "circuito" es constante y por lo tanto el flujo a través del circuito no cambia con el tiempo.
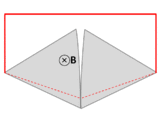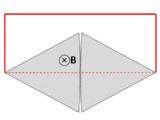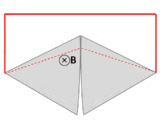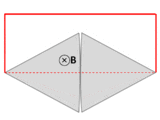
Un alambre (líneas rojas sólidas) se conecta a dos placas de metal táctil (plata) para formar un circuito. Todo el sistema se sienta en un campo magnético uniforme, normal a la página. Si el camino abstracto $\partial$ sigue el camino primario del flujo actual (marcado en rojo), luego el flujo magnético a través de este camino cambia dramáticamente a medida que las placas se giran, sin embargo el emf es casi cero. Después Feynman Conferencias sobre Física

Uno puede analizar ejemplos como estos cuidando que el camino $\partial$ se mueve con la misma velocidad que el material. Alternativamente, siempre se puede calcular correctamente el emf combinando la ley de fuerza Lorentz con la ecuación Maxwell-Faraday:

{displaystyle {mathcal {E}}=int _{partial Sigma }(mathbf {E} +mathbf {v} _{m}times mathbf {B})cdot mathrm {d} mathbf {l} =-int _{Sigma }{frac {partial mathbf {B} }{partial t}}cdot mathrm {d} Sigma +oint _{partial Sigma }(mathbf {v} _{m}times mathbf {B})cdot mathrm {d} mathbf {l} }

donde "es muy importante notar que (1) $[v m]$ es la velocidad del conductor... no la velocidad del elemento de ruta $d l$ y (2) en general, el derivado parcial con respecto al tiempo no se puede mover fuera de la integral ya que el área es una función del tiempo."

Ley de Faraday y relatividad

Dos fenómenos

La ley de Faraday es una ecuación única que describe dos fenómenos diferentes: la fem de movimiento generada por una fuerza magnética sobre un cable en movimiento (ver la fuerza de Lorentz) y el transformador. fem generada por una fuerza eléctrica debido a un campo magnético cambiante (descrita por la ecuación de Maxwell-Faraday).

James Clerk Maxwell llamó la atención sobre este hecho en su artículo de 1861 Sobre las líneas físicas de fuerza. En la segunda mitad de la Parte II de ese artículo, Maxwell da una explicación física separada para cada uno de los dos fenómenos.

En algunos libros de texto modernos se hace referencia a estos dos aspectos de la inducción electromagnética. Como afirma Richard Feynman:

Así que la "regla de flujo" que el emf en un circuito es igual a la tasa de cambio del flujo magnético a través del circuito aplica si el flujo cambia porque el campo cambia o porque el circuito se mueve (o ambos)...
Sin embargo, en nuestra explicación de la norma hemos utilizado dos leyes completamente distintas para los dos casos – $v \times B$ para "movimientos de circuito" y $Levántate \times E = t B$ para "cambios de campo".
No sabemos ningún otro lugar en la física donde un principio general tan simple y preciso requiere para su comprensión real un análisis en términos de dos fenómenos diferentes.
—Richard P. Feynman, El Feynman Conferencias sobre Física

Explicación basada en el formalismo cuatridimensional

En el caso general, explicación de la motional emf apariencia por acción de la fuerza magnética sobre los cargos en el alambre móvil o en el circuito que cambia su área es insatisfactoria. De hecho, los cargos en el alambre o en el circuito podrían estar completamente ausentes, entonces el efecto de inducción electromagnética desaparecerá en este caso? Esta situación se analiza en el artículo, en el que, al escribir las ecuaciones integrales del campo electromagnético en una forma covariante cuatridimensional, en la ley de Faraday el derivado total del flujo magnético a través del circuito aparece en lugar del derivado de tiempo parcial. Así, la inducción electromagnética aparece cuando el campo magnético cambia con el tiempo o cuando el área del circuito cambia. Desde el punto de vista físico, es mejor hablar no sobre el emf de inducción, sino sobre la fuerza de campo eléctrico inducida ${textstyle mathbf {E} =-nabla {mathcal {E}}-{frac {partial mathbf {A} }{partial t}}}$ , que ocurre en el circuito cuando el flujo magnético cambia. En este caso, la contribución a ${displaystyle mathbf {E} }$ del cambio en el campo magnético se hace a través del término ${textstyle -{frac {partial mathbf {A} }{partial t}}}$ Donde ${displaystyle mathbf {A} }$ es el potencial vectorial. Si el área del circuito está cambiando en caso del campo magnético constante, entonces alguna parte del circuito está inevitablemente en movimiento, y el campo eléctrico ${displaystyle mathbf {E} }$ emerge en esta parte del circuito en el marco de referencia comoving K’ como resultado de la transformación de Lorentz del campo magnético ${displaystyle mathbf {B} }$ , presente en el marco de referencia estacionario K, que pasa por el circuito. La presencia del campo ${displaystyle mathbf {E} }$ en K’ se considera como resultado del efecto de inducción en el circuito de movimiento, independientemente de si los cargos están presentes en el circuito o no. En el circuito de conducción, el campo ${displaystyle mathbf {E} }$ causa moción de los cargos. En el marco de referencia K, se parece a la apariencia de emf de la inducción ${displaystyle {mathcal {E}}}$ , el gradiente de que en forma ${displaystyle -nabla {mathcal {E}}}$ , tomado a lo largo del circuito, parece generar el campo ${displaystyle mathbf {E} }$ .

La visión de Einstein

La reflexión sobre esta aparente dicotomía fue uno de los principales caminos que llevaron a Albert Einstein a desarrollar una relatividad especial:

Se sabe que la electrodinámica de Maxwell —como generalmente se entiende en la actualidad— cuando se aplica a los cuerpos móviles, conduce a asimetrías que no parecen ser inherentes a los fenómenos. Tome, por ejemplo, la acción electrodinámica recíproca de un imán y un conductor.
El fenómeno observable aquí depende sólo del movimiento relativo del conductor y del imán, mientras que la vista consuetudinaria distingue claramente entre los dos casos en los que el uno o el otro de estos cuerpos está en movimiento. Porque si el imán está en movimiento y el conductor en reposo, surge en el barrio del imán un campo eléctrico con cierta energía definida, produciendo una corriente en los lugares donde se ubican partes del conductor.
Pero si el imán es estacionario y el conductor en movimiento, ningún campo eléctrico surge en el barrio del imán. En el conductor, sin embargo, encontramos una fuerza electromotiva, a la que en sí misma no hay energía correspondiente, pero que da lugar —asumiendo la igualdad de movimiento relativo en los dos casos discutidos— a corrientes eléctricas del mismo camino e intensidad que las producidas por las fuerzas eléctricas en el caso anterior.
Ejemplos de este tipo, junto con intentos infructuosos de descubrir cualquier movimiento de la tierra relativo al "médium ligero", sugieren que los fenómenos de la electrodinámica así como de la mecánica no poseen propiedades correspondientes a la idea del reposo absoluto.
—Albert Einstein, En la electrodinámica de los cuerpos de movimiento