Ley de Hess

Una representación de la ley de Hess (donde H representa enthalpy)

Ley de Hess de la suma de calor constante, también conocida simplemente como Hess' ley, es una relación en química física que lleva el nombre de Germain Hess, un químico y médico ruso nacido en Suiza que la publicó en 1840. La ley establece que el cambio de entalpía total durante el curso completo de una reacción química es independiente de la secuencia de pasos dados.

La ley de Hess ahora se entiende como una expresión del hecho de que la entalpía de un proceso químico es independiente del camino tomado desde el estado inicial hasta el final (es decir, la entalpía es una función de estado). De acuerdo con la primera ley de la termodinámica, el cambio de entalpía en un sistema debido a una reacción a presión constante es igual al calor absorbido (o al negativo del calor liberado), que puede determinarse por calorimetría para muchas reacciones. Los valores generalmente se establecen para reacciones con las mismas temperaturas y presiones iniciales y finales (mientras que se permite que las condiciones varíen durante el curso de las reacciones). La ley de Hess se puede usar para determinar la energía total requerida para una reacción química que se puede dividir en pasos sintéticos que son individualmente más fáciles de caracterizar. Esto permite la compilación de entalpías estándar de formación, que pueden usarse para predecir el cambio de entalpía en síntesis complejas.

Teoría

La ley de Hess establece que el cambio de entalpía en una reacción química es el mismo independientemente de si la reacción se lleva a cabo en un solo paso o en varios pasos, siempre que los estados inicial y final de los reactivos y productos sean los mismos.. La entalpía es una propiedad extensiva, lo que significa que su valor es proporcional al tamaño del sistema. Debido a esto, el cambio de entalpía es proporcional al número de moles que participan en una reacción dada.

En otras palabras, si se produce un cambio químico por varias rutas diferentes, el cambio de entalpía general es el mismo, independientemente de la ruta por la que se produzca el cambio químico (siempre que las condiciones inicial y final sean las mismas). Si esto no fuera cierto, entonces se podría violar la primera ley de la termodinámica.

La ley de Hess permite calcular el cambio de entalpía (ΔH) de una reacción incluso cuando no se puede medir directamente. Esto se logra realizando operaciones algebraicas básicas basadas en las ecuaciones químicas de las reacciones utilizando valores previamente determinados para las entalpías de formación.

La combinación de ecuaciones químicas conduce a una ecuación neta o global. Si los cambios enthalpy son conocidos por todas las ecuaciones en la secuencia, su suma será el cambio enthalpy para la ecuación neta. Si el cambio enthalpy neto es negativo (<math alttext="{displaystyle Delta H_{text{net}}Δ Δ Hneto.0{displaystyle Delta H_{text{net} {0}<img alt="{displaystyle Delta H_{text{net}}), la reacción es exotérmica y es más probable que sea espontánea; positivo ΔH los valores corresponden a las reacciones endotérmicas. (La entropía también juega un papel importante en la determinación de la espontaneidad, ya que algunas reacciones con un cambio positivo enthalpy son sin embargo espontáneas debido a un aumento entropía en el sistema de reacción.)

Uso de entalpías de formación

La ley de Hess establece que los cambios enthalpy son aditivos. Así el valor de Δ Δ H{displaystyle Delta H} para una sola reacción se puede calcular a partir de entalpies tabulados de formación de productos y reaccionarios de la siguiente manera:

Δ Δ Hreacción⊖ ⊖ =.. .. pΔ Δ Hf()p)⊖ ⊖ − − .. .. rΔ Δ Hf()r)⊖ ⊖ {displaystyle Delta H_{text{reaction} {ominus} }=sum nu _{text{p} Delta H_{mathrm {f} , {text{p}} {ominus }-sum nu _{text{r}} Delta H_{mathrm {f} , {text{r}} {ominus }}

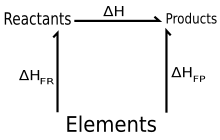
Aquí, la primera suma es sobre todos los productos p y la segunda sobre todos los reaccionarios r, .. p{displaystyle nu _{p}} es el coeficiente esteichiométrico del producto p, .. r{displaystyle nu _{text{r}} es el coeficiente esteichiométrico de reaccionante r, Δ Δ Hf()p){displaystyle Delta H_{f(p)}} es la enthalpy de la formación del producto p, Δ Δ Hf()r){displaystyle Delta H_{f(r)} es el enthalpy de la formación del reaccionante r, y el ^o superscript indica valores de estado estándar. Esto puede considerarse como la suma de dos reacciones (real o ficticias):

Reactantes → Elementos (en sus estados estándar)

Δ Δ HRE⊖ ⊖ =− − .. .. rΔ Δ Hf()r)⊖ ⊖ {displaystyle Delta H_{text{RE} {ominus} }=-sum nu _{text{r} Delta H_{mathrm {f} , {text{r}} {ominus }}

y Elementos → Productos

Δ Δ HEP⊖ ⊖ =.. .. pΔ Δ Hf()p)⊖ ⊖ {displaystyle Delta H_{text{EP} {ominus }=sum nu _{text{p} Delta H_{mathrm {f} , {text{p}} {ominus }

Ejemplos

1. Dado:
   1. C_grafito + O₂ → CO₂g) (Δ)H = −393.5 kJ/mol) (paso directo)
   2. C_grafito + 1/2 O₂ → CO(g) (ΔH = 110,5 kJ/mol)
   3. CO(g) +1/2 O₂ → CO₂g) (Δ)H = 283,0 kJ/mol)

   La reacción a) es la suma de las reacciones b) y c), para las cuales el total ΔH = −393.5 kJ/mol, que es igual a ΔH en a).

2. Dado:
   • B₂O₃s) + 3H₂O(g) → 3O₂g) + B₂H₆g) (Δ)H = 2035 kJ/mol)
   • H₂O...l) → H₂O(g) (ΔH = 44 kJ/mol)
   • H₂g) + 1/2 O₂g) → H₂O...l(Δ)H = 286 kJ/mol)
   • 2B(s) + 3H₂g) → B₂H₆g) (Δ)H = 36 kJ/mol)
   Encontrar el ΔH_f de:
   • 2B(s) + 3/2 O₂g) → B₂O₃s)
   Después de multiplicar las ecuaciones (y sus cambios enthalpy) por factores apropiados y revertir la dirección cuando sea necesario, el resultado es:
   • B₂H₆g) + 3O₂g) → B₂O₃s) + 3H₂O(g) (ΔH = 2035 × (−1) = 2035 kJ/mol)
   • 3H₂O(g) → 3H₂O...l(Δ)H = 44 × (−3) = 132 kJ/mol)
   • 3H₂O...l) → 3H₂g) + (3/2) O₂g) (Δ)H = −286 × - 3) = 858 kJ/mol)
   • 2B(s) + 3H₂g) → B₂H₆g) (Δ)H = 36 kJ/mol)
   Añadiendo estas ecuaciones y cancelando los términos comunes en ambos lados, obtenemos
   • 2B(s) + 3/2 O₂g) → B₂O₃s) (ΔH = −1273 kJ/mol)

Extensión a energía libre y entropía

Los conceptos de la ley de Hess se pueden expandir para incluir cambios en la entropía y en la energía libre de Gibbs, ya que también son funciones de estado. El ciclo termodinámico de Bordwell es un ejemplo de tal extensión que aprovecha los equilibrios fácilmente medidos y los potenciales redox para determinar valores de energía libre de Gibbs experimentalmente inaccesibles. Combinando los valores de ΔG^o de los ciclos termodinámicos de Bordwell y ΔH^o Los valores encontrados con la ley de Hess pueden ser útiles para determinar los valores de entropía que no se han medido directamente y, por lo tanto, deben calcularse a través de caminos alternativos.

Para la energía libre:

Δ Δ Greacción⊖ ⊖ =.. .. pΔ Δ Gf()p)⊖ ⊖ − − .. .. rΔ Δ Gf()r)⊖ ⊖ .{displaystyle Delta G_{text{reaction}{ominus }=sum nu _{text{p} Delta G_{mathrm {f} , {text{p}} {ominus }-sum nu _{text{r}} Delta G_{mathrm {f} ,({text{r})} {ominus }.}

Para la entropía, la situación es un poco diferente. Debido a que la entropía se puede medir como un valor absoluto, no relativo a los de los elementos en sus estados de referencia (como con ΔH^o y Δ G^o), no hay necesidad de usar la entropía de formación; uno simplemente usa las entropías absolutas para productos y reactivos:

Δ Δ Sreacción⊖ ⊖ =.. .. pS()p)⊖ ⊖ − − .. .. rS()r)⊖ ⊖ .{displaystyle Delta S_{text{reaction} {ominus} }=sum nu _{text{p}S_{ {text{p}}}{ominus }-sum nu _{text{r} {text{})} {ominus }

Aplicaciones

La ley de Hess es útil para determinar las entalpías de lo siguiente:

1. Calentadores de formación de intermediarios inestables como CO_g) y NO_g).
2. Calentar los cambios en las transiciones de fase y las transiciones alotrópicas.
3. Energías de celo de sustancias iónicas mediante la construcción de ciclos de Born-Haber si se conoce la afinidad de electrones para formar el anión, o
4. Afinidades de electrones usando un ciclo Nacido-Haber con una energía teórica de celo.