Lenguaje formal

Estructura de la frase sintácticamente bien formada, aunque no sensible, en inglés, "Las ideas verdes incoloras duermen furiosamente" (Ejemplo histórico de Chomsky 1957).

En lógica, matemáticas, informática y lingüística, un lenguaje formal consta de palabras cuyas letras se toman de un alfabeto y están bien formadas de acuerdo con un conjunto específico de reglas.

El alfabeto de un lenguaje formal consta de símbolos, letras o tokens que se concatenan en cadenas del lenguaje. Cada cadena concatenada de símbolos de este alfabeto se denomina palabra, y las palabras que pertenecen a un lenguaje formal particular a veces se denominan palabras bien formadas o fórmulas bien formadas. Un lenguaje formal a menudo se define por medio de una gramática formal, como una gramática regular o una gramática libre de contexto, que consiste en sus reglas de formación.

En informática, los lenguajes formales se utilizan, entre otros, como base para definir la gramática de los lenguajes de programación y las versiones formalizadas de subconjuntos de lenguajes naturales en los que las palabras del lenguaje representan conceptos asociados con significados o semánticas particulares. En la teoría de la complejidad computacional, los problemas de decisión se definen típicamente como lenguajes formales, y las clases de complejidad se definen como los conjuntos de lenguajes formales que pueden ser analizados por máquinas con un poder computacional limitado. En la lógica y los fundamentos de las matemáticas, los lenguajes formales se utilizan para representar la sintaxis de los sistemas axiomáticos, y el formalismo matemático es la filosofía de que todas las matemáticas pueden reducirse a la manipulación sintáctica de los lenguajes formales de esta manera.

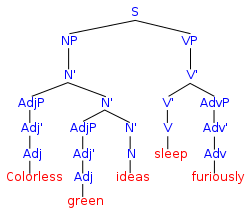
El campo de la teoría formal del lenguaje estudia principalmente los aspectos puramente sintácticos de dichos lenguajes, es decir, sus patrones estructurales internos. La teoría del lenguaje formal surgió de la lingüística, como una forma de comprender las regularidades sintácticas de los lenguajes naturales.

Historia

En el siglo XVII, Gottfried Leibniz imaginó y describió la charactera universalis, un lenguaje universal y formal que utilizaba pictografías. Durante este período, Carl Friedrich Gauss también investigó el problema de los códigos de Gauss.

Gottlob Frege intentó realizar las ideas de Leibniz, a través de un sistema de notación descrito por primera vez en Begriffsschrift (1879) y más desarrollado en sus dos volúmenes Grundgesetze der Arithmetik (1893/1903). Esto describía un "lenguaje formal del lenguaje puro."

En la primera mitad del siglo XX, se realizaron varios desarrollos relacionados con los lenguajes formales. Axel Thue publicó cuatro artículos relacionados con las palabras y el lenguaje entre 1906 y 1914. El último de ellos introdujo lo que Emil Post denominó más tarde 'Sistemas Thue' y proporcionó un ejemplo temprano de un problema indecidible. Post usaría más tarde este artículo como base para una prueba de 1947 "que el problema verbal de los semigrupos era recursivamente insoluble", y luego ideó el sistema canónico para la creación de lenguajes formales.

Noam Chomsky ideó una representación abstracta de los lenguajes formales y naturales, conocida como la jerarquía de Chomsky. En 1959, John Backus desarrolló la forma Backus-Naur para describir la sintaxis de un lenguaje de programación de alto nivel, siguiendo su trabajo en la creación de FORTRAN. Peter Naur inventó un esquema similar en 1960.

Palabras sobre un alfabeto

Un alfabeto, en el contexto de los lenguajes formales, puede ser cualquier conjunto, aunque a menudo tiene sentido usar un alfabeto en el sentido habitual de la palabra, o más generalmente cualquier codificación de caracteres finitos como como ASCII o Unicode. Los elementos de un alfabeto se llaman sus letras. Un alfabeto puede contener un número infinito de elementos; sin embargo, la mayoría de las definiciones en la teoría del lenguaje formal especifican alfabetos con un número finito de elementos y la mayoría de los resultados se aplican solo a ellos.

Una palabra sobre un alfabeto puede ser cualquier secuencia finita (es decir, una cadena) de letras. El conjunto de todas las palabras sobre un alfabeto Σ generalmente se denota por Σ^* (usando la estrella de Kleene). La longitud de una palabra es el número de letras que la componen. Para cualquier alfabeto, solo hay una palabra de longitud 0, la palabra vacía, que a menudo se denota con e, ε, λ o incluso Λ. Por concatenación se pueden combinar dos palabras para formar una nueva palabra, cuya longitud es la suma de las longitudes de las palabras originales. El resultado de concatenar una palabra con la palabra vacía es la palabra original.

En algunas aplicaciones, especialmente en lógica, el alfabeto también se conoce como vocabulario y las palabras se conocen como fórmulas u oraciones; esto rompe la metáfora de letra/palabra y la reemplaza por una metáfora de palabra/oración.

Definición

Un lenguaje formal L sobre un alfabeto Σ es un subconjunto de Σ^*, es decir, un conjunto de palabras sobre ese alfabeto. A veces, los conjuntos de palabras se agrupan en expresiones, mientras que se pueden formular reglas y restricciones para la creación de "expresiones bien formadas".

En informática y matemáticas, que no suelen tratar con lenguajes naturales, el adjetivo "formal" a menudo se omite por redundante.

Si bien la teoría del lenguaje formal generalmente se ocupa de los lenguajes formales que se describen mediante algunas reglas sintácticas, la definición real del concepto "lenguaje formal" es solo como el anterior: un conjunto (posiblemente infinito) de cadenas de longitud finita compuestas de un alfabeto dado, ni más ni menos. En la práctica, hay muchos lenguajes que pueden describirse mediante reglas, como lenguajes regulares o lenguajes libres de contexto. La noción de una gramática formal puede estar más cerca del concepto intuitivo de un "lenguaje" uno descrito por reglas sintácticas. Por un abuso de la definición, a menudo se piensa que un lenguaje formal particular está equipado con una gramática formal que lo describe.

Ejemplos

Las siguientes reglas describen un lenguaje formal L sobre el alfabeto Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:

• Cada cadena no vacía que no contiene "+" o "=" y no comienza con "0" está enL.
• La cuerda "0" está enL.
• Una cadena que contiene "=" está enL si y sólo si hay exactamente un "=", y separa dos cadenas válidas deL.
• Una cadena que contiene "+" pero no "=" está enL si y sólo si cada "+" en la cuerda separa dos cadenas válidas deL.
• No hay cuerda.L aparte de los implicados en las reglas anteriores.

Bajo estas reglas, la cadena "23+4=555" está en L, pero la cadena "=234=+" no es. Este lenguaje formal expresa números naturales, sumas bien formadas e igualdades de suma bien formadas, pero expresa solo su apariencia (su sintaxis), no lo que significan (semántica). Por ejemplo, en ninguna parte de estas reglas hay ninguna indicación de que "0" significa el número cero, "+" significa suma, "23+4=555" es falso, etc

Construcciones

Para lenguajes finitos, uno puede enumerar explícitamente todas las palabras bien formadas. Por ejemplo, podemos describir un idioma L simplemente como L = {a, b, ab, cba}. El caso degenerado de esta construcción es el lenguaje vacío, que no contiene ninguna palabra (L = ∅).

Sin embargo, incluso en un alfabeto finito (no vacío) como Σ = {a, b}, hay un número infinito de palabras de longitud finita que pueden expresarse potencialmente: "a", & #34;abb", "ababba", "aaababbbbaab",.... Por lo tanto, los lenguajes formales suelen ser infinitos, y describir un lenguaje formal infinito no es tan simple como escribir L = {a, b, ab, cba}. Estos son algunos ejemplos de lenguajes formales:

• L =^*, el conjunto de Todos - palabras sobre la República;
• L = {a}^* *ⁿ}, donde n rangos sobre los números naturales y "aⁿsignifica "a" repetido n tiempos (este es el conjunto de palabras que consiste sólo del símbolo "a");
• el conjunto de programas sintacticamente correctos en un lenguaje de programación dado (la sintaxis de la cual se define generalmente por una gramática sin contexto);
• el conjunto de entradas sobre las cuales una determinada máquina de Turing se detiene; o
• el conjunto de cuerdas máximas de caracteres alfanuméricos ASCII en esta línea, es decir,
  el set {el, set, de, maximal, strings, alfanumérico, ASCII, caracteres, en, este, línea, i, e}.

Formalismos de especificación del lenguaje

Los lenguajes formales se utilizan como herramientas en múltiples disciplinas. Sin embargo, la teoría del lenguaje formal rara vez se ocupa de lenguajes particulares (excepto como ejemplos), sino que se ocupa principalmente del estudio de varios tipos de formalismos para describir lenguajes. Por ejemplo, un lenguaje se puede dar como

• esas cadenas generadas por alguna gramática formal;
• esas cadenas descritas o coinciden con una expresión regular particular;
• esas cadenas aceptadas por algún autómata, como una máquina de Turing o un autómata de estado finito;
• aquellas cadenas para las cuales algún procedimiento de decisión (un algoritmo que hace una secuencia de preguntas relacionadas con SÍ/NO) produce la respuesta SÍ.

Las preguntas típicas que se hacen sobre tales formalismos incluyen:

• ¿Cuál es su poder expresivo? (Can formalism X describir cada lenguaje que formalismo Y ¿Puede describir? ¿Puede describir otros idiomas?)
• ¿Cuál es su reconocimiento? (Cuán difícil es decidir si una palabra determinada pertenece a un idioma descrito por el formalismo X?
• ¿Cuál es su comparabilidad? (Cuán difícil es decidir si dos idiomas, uno descrito en el formalismo X y uno en formalismo Y, o dentro X otra vez, ¿es en realidad el mismo idioma?).

Sorprendentemente, a menudo, la respuesta a estos problemas de decisión es "no se puede hacer en absoluto", o "es extremadamente costoso" (con una caracterización de lo caro). Por lo tanto, la teoría del lenguaje formal es un área de aplicación importante de la teoría de la computabilidad y la teoría de la complejidad. Los lenguajes formales pueden clasificarse en la jerarquía de Chomsky según el poder expresivo de su gramática generativa, así como la complejidad de su autómata de reconocimiento. Las gramáticas independientes del contexto y las gramáticas regulares proporcionan un buen compromiso entre la expresividad y la facilidad de análisis, y se utilizan ampliamente en aplicaciones prácticas.

Operaciones en idiomas

Ciertas operaciones en idiomas son comunes. Esto incluye las operaciones de conjunto estándar, como unión, intersección y complemento. Otra clase de operación es la aplicación de elementos de operaciones de cadena.

Ejemplos: supongan L1{displaystyle L_{1} y L2{displaystyle L_{2} son idiomas sobre algún alfabeto común .. {displaystyle Sigma }.

• El concatenación L1⋅ ⋅ L2{displaystyle L_{1}cdot L_{2} consiste en todas las cuerdas de la forma vw{displaystyle vw} Donde v{displaystyle v} es una cuerda de L1{displaystyle L_{1} y w{displaystyle w} es una cuerda de L2{displaystyle L_{2}.
• El intersección L1∩ ∩ L2{displaystyle L_{1}cap L_{2} de L1{displaystyle L_{1} y L2{displaystyle L_{2} consiste en todas las cuerdas que se contienen en ambos idiomas
• El complemento ¬ ¬ L1{displaystyle neg L_{1} de L1{displaystyle L_{1} con respecto a .. {displaystyle Sigma } consiste en todas las cuerdas sobre .. {displaystyle Sigma } que no están L1{displaystyle L_{1}.
• La estrella kleene: el lenguaje que consiste en todas las palabras que son concatenaciones de cero o más palabras en el idioma original;
• Reversal:
  • Vamos ε sea la palabra vacía, entonces ε ε R=ε ε {displaystyle varepsilon ^{R}=varepsilon }, y
  • para cada palabra no vacía w=σ σ 1⋯ ⋯ σ σ n{displaystyle w=sigma _{1}cdots sigma _{n} (donde) σ σ 1,...... ,σ σ n{displaystyle sigma _{1},ldotssigma ¿Qué?son elementos de algún alfabeto), wR=σ σ n⋯ ⋯ σ σ 1{displaystyle w^{R}=sigma _{n}cdots sigma ¿Qué?,
  • entonces para un lenguaje formal L{displaystyle L., LR={}wR▪ ▪ w▪ ▪ L}{displaystyle ¿Qué?.
• Homomorfismo de cuerda

Estas operaciones de cadenas se utilizan para investigar las propiedades de cierre de las clases de lenguajes. Una clase de lenguajes se cierra bajo una operación particular cuando la operación, aplicada a los lenguajes en la clase, siempre produce un lenguaje en la misma clase nuevamente. Por ejemplo, se sabe que los lenguajes libres de contexto están cerrados bajo unión, concatenación e intersección con lenguajes regulares, pero no cerrados bajo intersección o complemento. La teoría de los tríos y las familias abstractas de lenguas estudia las propiedades de clausura más comunes de las familias de lenguas por derecho propio.

Propiedades de cierre de las familias de idiomas (L1{displaystyle L_{1} Op L2{displaystyle L_{2} donde ambos L1{displaystyle L_{1} y L2{displaystyle L_{2} están en la familia de idiomas dada por la columna). Después de Hopcroft y Ullman.

Operación		Recursos ordinarios	DCFL	CFL	IND	CSL	recursivo	RE
Unión	L1∪ ∪ L2={}w▪ ▪ w▪ ▪ L1Alternativa Alternativa w▪ ▪ L2}{displaystyle L_{1}cup L_{2}={wmid win L_{1}lor win L_{2}	Sí.	No	Sí.	Sí.	Sí.	Sí.	Sí.
Intersección	L1∩ ∩ L2={}w▪ ▪ w▪ ▪ L1∧ ∧ w▪ ▪ L2}{displaystyle L_{1}cap L_{2}={wmid win L_{1}land win L_{2}	Sí.	No	No	No	Sí.	Sí.	Sí.
Complemento	¬ ¬ L1={}w▪ ▪ w∉L1}{displaystyle neg L_{1}={wmid wnot in L_{1}}	Sí.	Sí.	No	No	Sí.	Sí.	No
Concatenación	L1⋅ ⋅ L2={}wz▪ ▪ w▪ ▪ L1∧ ∧ z▪ ▪ L2}{displaystyle L_{1}cdot L_{2}={wzmid win L_{1}land zin L_{2}	Sí.	No	Sí.	Sí.	Sí.	Sí.	Sí.
Kleene star	L1Alternativa Alternativa ={}ε ε }∪ ∪ {}wz▪ ▪ w▪ ▪ L1∧ ∧ z▪ ▪ L1Alternativa Alternativa }{displaystyle L_{1}{*}={varepsilon {fnfn}fnfn}fn}fn1} {fn}}}\fn}	Sí.	No	Sí.	Sí.	Sí.	Sí.	Sí.
homomorfismo h{displaystyle h}	h()L1)={}h()w)▪ ▪ w▪ ▪ L1}{displaystyle h(L_{1}={h(w)mid win L_{1}}	Sí.	No	Sí.	Sí.	No	No	Sí.
Homomorfismo libre de ε (cadena) h{displaystyle h}	h()L1)={}h()w)▪ ▪ w▪ ▪ L1}{displaystyle h(L_{1}={h(w)mid win L_{1}}	Sí.	No	Sí.	Sí.	Sí.	Sí.	Sí.
Sustitución φ φ {displaystyle varphi }	φ φ ()L1)=⋃ ⋃ σ σ 1⋯ ⋯ σ σ n▪ ▪ L1φ φ ()σ σ 1)⋅ ⋅ ...... ⋅ ⋅ φ φ ()σ σ n){displaystyle varphi (L_{1})=bigcup _{sigma _{1}cdots sigma _{n}in L_{1}varphi (sigma _{1})cdot ldot varphi (sigma _{n})}}	Sí.	No	Sí.	Sí.	Sí.	No	Sí.
Homorfismo inverso h− − 1{displaystyle h^{-1}	h− − 1()L1)=⋃ ⋃ w▪ ▪ L1h− − 1()w){displaystyle h^{-1}(L_{1})=bigcup _{win L_{1}h^{-1}(w)}	Sí.	Sí.	Sí.	Sí.	Sí.	Sí.	Sí.
Inversión	LR={}wR▪ ▪ w▪ ▪ L}{displaystyle ¿Qué?	Sí.	No	Sí.	Sí.	Sí.	Sí.	Sí.
Intersección con un idioma regular R{displaystyle R.	L∩ ∩ R={}w▪ ▪ w▪ ▪ L∧ ∧ w▪ ▪ R}{displaystyle Lcap R={wmid win Lland win R}	Sí.	Sí.	Sí.	Sí.	Sí.	Sí.	Sí.

Aplicaciones

Lenguajes de programación

Un compilador normalmente tiene dos componentes distintos. Un analizador léxico, a veces generado por una herramienta como lex, identifica los tokens de la gramática del lenguaje de programación, p. identificadores o palabras clave, literales numéricos y de cadena, signos de puntuación y de operador, que a su vez se especifican mediante un lenguaje formal más simple, generalmente por medio de expresiones regulares. En el nivel conceptual más básico, un analizador, a veces generado por un generador de analizadores como yacc, intenta decidir si el programa fuente es sintácticamente válido, es decir, si está bien formado con respecto al lenguaje de programación. gramática para la que se construyó el compilador.

Por supuesto, los compiladores hacen más que simplemente analizar el código fuente; generalmente lo traducen a algún formato ejecutable. Debido a esto, un analizador generalmente genera más de una respuesta de sí/no, generalmente un árbol de sintaxis abstracta. Esto es utilizado por las etapas posteriores del compilador para generar eventualmente un ejecutable que contiene código de máquina que se ejecuta directamente en el hardware, o algún código intermedio que requiere una máquina virtual para ejecutarse.

Teorías formales, sistemas y pruebas

Este diagrama muestra las divisiones sintácticas dentro de un sistema formal. Las cuerdas de símbolos pueden dividirse ampliamente en fórmulas sin sentido y bien formadas. El conjunto de fórmulas bien formadas se divide en teoremas y no teoremas.

En lógica matemática, una teoría formal es un conjunto de oraciones expresadas en un lenguaje formal.

A sistema formal (también llamado a cálculo lógico, o un sistema lógico) consiste en un lenguaje formal junto con un aparato deductivo (también llamado un sistema deductivo). El aparato deductivo puede consistir en un conjunto de reglas de transformación, que pueden ser interpretadas como reglas válidas de inferencia, o un conjunto de axiomas, o tener ambos. Un sistema formal se utiliza para derivar una expresión de una o más expresiones. Aunque un lenguaje formal puede ser identificado con sus fórmulas, un sistema formal no puede ser identificado igualmente por sus teoremas. Dos sistemas formales FS{displaystyle {mathcal {}}} y FS.{displaystyle {mathcal {}}} puede tener todos los mismos teoremas y, sin embargo, difieren de alguna manera significativa-teorética de la prueba (una fórmula A puede ser una consecuencia sintáctica de una fórmula B en uno pero no otro por ejemplo).

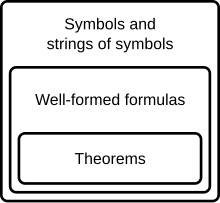
Una prueba formal o derivación es una secuencia finita de fórmulas bien formadas (que pueden interpretarse como oraciones o proposiciones), cada una de las cuales es un axioma o sigue de las fórmulas precedentes en la secuencia por una regla de inferencia. La última oración de la secuencia es un teorema de un sistema formal. Las pruebas formales son útiles porque sus teoremas pueden interpretarse como proposiciones verdaderas.

Interpretaciones y modelos

Los lenguajes formales son completamente sintácticos por naturaleza, pero se les puede dar una semántica que dé significado a los elementos del lenguaje. Por ejemplo, en lógica matemática, el conjunto de fórmulas posibles de una lógica particular es un lenguaje formal, y una interpretación asigna un significado a cada una de las fórmulas, generalmente, un valor de verdad.

El estudio de las interpretaciones de los lenguajes formales se denomina semántica formal. En lógica matemática, esto se hace a menudo en términos de teoría de modelos. En la teoría de modelos, los términos que aparecen en una fórmula se interpretan como objetos dentro de estructuras matemáticas, y las reglas de interpretación de composición fijas determinan cómo se puede derivar el valor de verdad de la fórmula a partir de la interpretación de sus términos; un modelo para una fórmula es una interpretación de los términos tal que la fórmula se vuelve verdadera.