Lema de la serpiente

El lema de la serpiente es una herramienta utilizada en matemáticas, particularmente en álgebra homológica, para construir sucesiones exactas largas. El lema de la serpiente es válido en todas las categorías abelianas y es una herramienta crucial en el álgebra homológica y sus aplicaciones, por ejemplo, en la topología algebraica. Los homomorfismos construidos con su ayuda se denominan generalmente homomorfismos de conexión.

Declaración

En una categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un campo dado), considere un diagrama conmutativo:

donde las filas son secuencias exactas y 0 es el objeto cero.

Entonces hay una secuencia exacta que relaciona los kernels y cokernels de a, b y c:

${displaystyle ker a~{color {Gray}longrightarrow ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ {d}{longrightarrow ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪♪ [Coker] a~{color {Gray}longrightarrow }~operatorname {coker} b~{color {Gray}longrightarrow }~operatorname {Coker} c}$

donde d es un homomorfismo, conocido como homomorfismo de conexión.

Además, si el morfismo f es un monomorfismo, entonces también el morfismo ${displaystyle ker a~{color {Gray}longrightarrow }~ker b)$, y si g ' es un epimorfismo, entonces lo es ${displaystyle operatorname {coker} ################################################################################################################################################################################################################################################################ {Coker} c}$.

Los cokernels aquí son: ${displaystyle operatorname {coker} a=A'/operatorname {im} a}$, ${displaystyle operatorname {coker} b=B/operatorname {im}b}$, ${displaystyle operatorname {coker} c=C'/operatorname {im} c}$.

Explicación del nombre

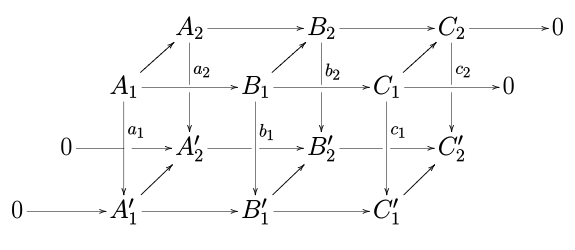
Para ver de dónde obtiene su nombre el lema de la serpiente, expanda el diagrama anterior de la siguiente manera:

y luego tenga en cuenta que la secuencia exacta que es la conclusión del lema se puede dibujar en este diagrama ampliado en la "S" forma de una serpiente deslizándose.

Construcción de los mapas

Los mapas entre los núcleos y los mapas entre los conúcleos son inducidos de manera natural por los mapas dados (horizontales) debido a la conmutatividad del diagrama. La exactitud de las dos sucesiones inducidas se deduce directamente de la exactitud de las filas del diagrama original. El enunciado importante del lema es que existe un homomorfismo de conexión d que completa la secuencia exacta.

En el caso de grupos o módulos abelianos sobre algún anillo, el mapa d se puede construir de la siguiente manera:

Seleccione un elemento x en ker c y visualícelo como un elemento de C; como g es sobreyectiva, existe y en B con g(y) = x. Debido a la conmutatividad del diagrama, tenemos g'(b(y)) = c (g(y)) = c(x) = 0 (ya que x está en el kernel de c), y por lo tanto b(y) está en el kernel de g' . Dado que la fila inferior es exacta, encontramos un elemento z en A' con f '(z) = b(y). z es único por la inyectividad de f '. Luego definimos d(x) = z + im(a). Ahora hay que comprobar que d está bien definido (es decir, d(x) solo depende de x y no en la elección de y), que es un homomorfismo, y que la secuencia larga resultante es exacta. Uno puede verificar rutinariamente la exactitud siguiendo el diagrama (vea la demostración del Lema 9.1).

Una vez hecho esto, se prueba el teorema para grupos o módulos abelianos sobre un anillo. Para el caso general, el argumento puede reformularse en términos de propiedades de flechas y cancelación en lugar de elementos. Alternativamente, uno puede invocar el teorema de incrustación de Mitchell.

Naturalidad

En las aplicaciones, a menudo es necesario demostrar que las secuencias exactas largas son "naturales" (en el sentido de transformaciones naturales). Esto se sigue de la naturalidad de la secuencia producida por el lema de la serpiente.

Si

es un diagrama conmutativo con filas exactas, entonces el lema de la serpiente se puede aplicar dos veces, al "frente" y al 'atrás', produciendo dos secuencias exactas largas; estos están relacionados por un diagrama conmutativo de la forma

Ejemplo

Vamos ${displaystyle k}$ ser campo, ${displaystyle V}$ ser un ${displaystyle k}$-Espacio del vencedor. ${displaystyle V}$ es ${displaystyle k[t]}$- Mobiliario por ${displaystyle t:Vto V}$ ser un ${displaystyle k}$- Transformación lineal, para que podamos tensor ${displaystyle V}$ y ${displaystyle k}$ sobre ${displaystyle k[t]}$.

${displaystyle Votimes _{k[t]}k=Votimes _{k[t]}(k[t]/(t)=V/tV=operatorname {coker} (t).}$

Dada una breve secuencia exacta ${displaystyle k}$- Espacios de vehículos ${displaystyle 0to Mto Nto Pto 0}$, podemos inducir una secuencia exacta ${displaystyle Motimes _{k[t]}kto Notimes _{k[t]}kto Potimes _{k[t]}kto 0}$ por la exactitud correcta del producto tensor. Pero la secuencia ${displaystyle 0to Motimes _{k[t]}kto Notimes _{k[t]}kto Potimes _{k[t]}kto 0}$ no es exacto en general. Por lo tanto, surge una pregunta natural. ¿Por qué esta secuencia no es exacta?

Según el diagrama anterior, podemos inducir una secuencia exacta ${displaystyle ker(t_{M})to ker(t_{N})to ker(t_{P})to Motimes _{k[t]}kto Notimes _{k[t]}kto Potimes _{k[t]}kto 0}$ aplicando el lema de la serpiente. Así, la lema de la serpiente refleja el fracaso del producto tensor para ser exacto.

En la categoría de grupos

Mientras que muchos resultados de álgebra homológica, como los cinco lemma o los nueve lemma, se sostienen para las categorías abelianas, así como en la categoría de grupos, la lema de serpiente no. De hecho, no existen coqueles arbitrarios. Sin embargo, uno puede reemplazar los coqueles por (izquierda) cosets ${displaystyle A'/operatorname {im} a$, ${displaystyle B'/operatorname {im} b$, y ${displaystyle C'/operatorname {im} c}$. Entonces el homomorfismo de conexión todavía se puede definir, y uno puede escribir una secuencia como en la declaración de la lema de la serpiente. Esto siempre será un complejo de cadena, pero puede que no sea exacto. La exactitud se puede afirmar, sin embargo, cuando las secuencias verticales en el diagrama son exactas, es decir, cuando las imágenes de a, b, y c son subgrupos normales.

Contraejemplo

Considere el grupo alternativo ${displaystyle A_{5}$: esto contiene un subgrupo isomorfo al grupo simétrico ${displaystyle S_{3}$, que a su vez se puede escribir como un producto semidirecto de grupos cíclicos: ${displaystyle S_{3}simeq C_{3}rtimes C_{2}$. Esto da lugar al siguiente diagrama con filas exactas:

${displaystyle {begin{matrix} tarde1 puntoto > {3} círculoto > {3} limitto 1\\cH00downarrow > }1to > âto > {3} {}}}}}}}}}}}$

Tenga en cuenta que la columna media no es exacta: ${displaystyle C_{2}$ no es un subgrupo normal en el producto semidirecto.

Desde ${displaystyle A_{5}$ es simple, la flecha vertical derecha tiene cokernel trivial. Mientras tanto, el grupo cociente ${displaystyle S_{3}/C_{3}$ es isomorfo a ${displaystyle C_{2}$. La secuencia en la declaración de la lema de la serpiente es por lo tanto

${displaystyle 1longrightarrow 1longrightarrow 1longrightarrow 1longrightarrow C_{2}longrightarrow 1}$,

que de hecho no es exacto.

En la cultura popular

El personaje de Jill Clayburgh enseña la prueba del lema de la serpiente al comienzo de la película de 1980 It's My Turn.