Lah número
En matemáticas, la Números, descubierto por Ivo Lah en 1954, son coeficientes que expresan crecientes factores en términos de caída de factores. También son los coeficientes de los n{displaystyle n}de los derivados de e1/x{displaystyle e^{1/x}.
Los números de Lah sin signo tienen un significado interesante en combinatoria: cuentan el número de formas en que un conjunto de n elementos se puede dividir en k subconjuntos linealmente ordenados no vacíos. Los números de Lah están relacionados con los números de Stirling.
Números Lah sin firmar (secuencia A105278 en el OEIS):
- L()n,k)=()n− − 1k− − 1)n!k!.{displaystyle L(n,k)={n-1 choose k-1}{frac ¡No!
Números Lah firmados (secuencia A008297 en el OEIS):
- L.()n,k)=()− − 1)n()n− − 1k− − 1)n!k!.{displaystyle L'(n,k)=(-1)^{n-1 choose k-1}{frac ¡No!
L(n, 1) siempre es n!; en la interpretación anterior, la única partición de {1, 2, 3} en 1 conjunto puede tener su conjunto ordenado de 6 maneras:
- {(1, 2, 3)}, {(1, 3, 2)}, {(2, 1, 3)}, {(2, 3, 1)}, {(3, 1, 2)} o {(3, 2, 1)}
L(3, 2) corresponde a las 6 particiones con dos partes ordenadas:
- {(1), (2, 3)}, {(1), (3, 2)}, {(2), (1, 3)}, {(2), (3, 1)}, { 3), (1, 2)} o { 3), (2, 1)}
L(n, n) siempre es 1 ya que, por ejemplo, dividir {1, 2, 3} en 3 no vacíos subconjuntos da como resultado subconjuntos de longitud 1.
- {(1), (2), (3)}
Al adaptar la notación de Karamata-Knuth para los números de Stirling, se ha propuesto utilizar la siguiente notación alternativa para los números de Lah:
Factoriales ascendentes y descendentes
Vamos x()n){displaystyle x^{(n)}} representar el factorial creciente x()x+1)()x+2)⋯ ⋯ ()x+n− − 1){displaystyle x(x+1)(x+2)cdots (x+n-1)} y dejar ()x)n{displaystyle (x)_{n} representa la caída factorial x()x− − 1)()x− − 2)⋯ ⋯ ()x− − n+1){displaystyle x(x-1)(x-2)cdots (x-n+1)}.
Entonces... x()n)=.. k=1nL()n,k)()x)k{displaystyle x^{(n)}=sum _{k=1}{n}L(n,k)(x)_{k} y ()x)n=.. k=1n()− − 1)n− − kL()n,k)x()k).{displaystyle (x)_{n}=sum _{k=1}{n}(-1)^{n-k}L(n,k)x^{(k)}
Por ejemplo,
Compare la tercera fila de la tabla de valores.
Identidades y relaciones
- L()n,k)=()n− − 1k− − 1)n!k!=()nk)()n− − 1)!()k− − 1)!=()nk)()n− − 1k− − 1)()n− − k)!{displaystyle L(n,k)={n-1 choose k-1}{frac {n} {k!}={n choose k}{frac {(n-1)}{(k-1)}}={n choose k}{n-1 choose k-1} (n-k)}
- L()n,k)=n!()n− − 1)!k!()k− − 1)!⋅ ⋅ 1()n− − k)!=()n!k!)2kn()n− − k)!{displaystyle L(n,k)={frac {n! {n-1)}{k!(k-1)}}cdot {frac {1}{(n-k)}=left({frac] {n}{k}}right)}{2}{frac {k} {n(n-k)}}
- L()n,k+1)=n− − kk()k+1)L()n,k).{displaystyle L(n,k+1)={frac {n-k}{k(k+1)}L(n,k). }
- L()n+1,k)=()n+k)L()n,k)+L()n,k− − 1){displaystyle L(n+1,k)=(n+k)L(n,k)+L(n,k-1)} Donde L()n,0)=0{displaystyle L(n,0)=0}, L()n,k)=0{displaystyle L(n,k)=0} para todos n}" xmlns="http://www.w3.org/1998/Math/MathML">k■n{displaystyle k]n}
n" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/66e81682bf174c978e9008ffb557ba4da2cf7478" style="vertical-align: -0.338ex; width:5.704ex; height:2.176ex;"/>, y L()1,1)=1.{displaystyle L(1,1)=1.}
- L()n,k)=.. j[nj]{}jk},{displaystyle L(n,k)=sum _{j}left[{n atop j}right]left{j atop k}right} Donde [nj]{displaystyle left[{n atop j}right] son los números Stirling del primer tipo y {}jk}{displaystyle left{j atop k}right} son los números del segundo tipo, L()0,0)=1{displaystyle L(0,0)=1}, y L()n,k)=0{displaystyle L(n,k)=0} para todos n}" xmlns="http://www.w3.org/1998/Math/MathML">k■n{displaystyle k]n}
n" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/66e81682bf174c978e9008ffb557ba4da2cf7478" style="vertical-align: -0.338ex; width:5.704ex; height:2.176ex;"/>.
- L()n,1)=n!{displaystyle L(n,1)=n!}
- L()n,2)=()n− − 1)n!/2{displaystyle L(n,2)=(n-1)n!/2}
- L()n,3)=()n− − 2)()n− − 1)n!/12{displaystyle L(n,3)=(n-2)(n-1)n!/12}
- L()n,n− − 1)=n()n− − 1){displaystyle L(n,n-1)=n(n-1)}
- L()n,n)=1{displaystyle L(n,n)=1}
- .. n≥ ≥ kL()n,k)xnn!=1k!()x1− − x)k{displaystyle sum _{ngeq k}L(n,k){frac {x^{n}{n}}={frac {1} {k}}left({frac {x}{1-x}right)}{k}}} {c}} {c} {c}} {c}}} {c}}}}}}}}}}}}}}}}c}}cc}}}}ccH00}}}}}c}}}}}}}}}}}}}}}}}}}}}}}}m}m}}}}}}}}}}}}}}}}}}}c}c}c}c}c}cc}}}c}c}c}}c}c}}}}c}c}c}}}c}c}ccccc}c}}}}}}}}}}}}}c}}}}}ccc}ccc}}}}}}}
Tabla de valores
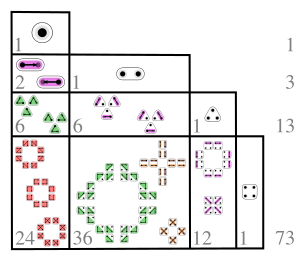
A continuación se muestra una tabla de valores para los números de Lah:
k n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||||
| 2 | 2 | 1 | ||||||||||
| 3 | 6 | 6 | 1 | |||||||||
| 4 | 24 | 36 | 12 | 1 | ||||||||
| 5 | 120 | 240 | 120 | 20 | 1 | |||||||
| 6 | 720 | 1800 | 1200 | 300 | 30 | 1 | ||||||
| 7 | 5040 | 15120 | 12600 | 4200 | 630 | 42 | 1 | |||||
| 8 | 40320 | 141120 | 141120 | 58800 | 11760 | 1176 | 56 | 1 | ||||
| 9 | 362880 | 1451520 | 1693440 | 846720 | 211680 | 28224 | 2016 | 72 | 1 | |||
| 10 | 3628800 | 16329600 | 21772800 | 12700800 | 3810240 | 635040 | 60480 | 3240 | 90 | 1 | ||
| 11 | 39916800 | 199584000 | 299376000 | 199584000 | 69854400 | 13970880 | 1663200 | 11880 | 4950 | 110 | 1 | |
| 12 | 479001600 | 2634508800 | 4390848000 | 3293136000 | 1317254400 | 307359360 | 43908480 | 3920400 | 217800 | 7260 | 132 | 1 |
Aplicación práctica reciente
En los últimos años, los números de Lah se han utilizado en la esteganografía para ocultar datos en imágenes. En comparación con alternativas como DCT, DFT y DWT, tiene menor complejidad:O()nlog n){displaystyle O(nlog n)}—del cálculo de sus coeficientes enteros. El Lah y Laguerre se transforman naturalmente en la descripción perturbadora de la dispersión cromática . En la óptica de Lah-Laguerre, tal enfoque acelera enormemente los problemas de optimización.
Contenido relacionado
Propiedad distributiva
Teorema del límite central
Función gamma




![{displaystyle L(n,k)=sum _{j=0}^{n}left[{begin{matrix}n\jend{matrix}}right]left{{begin{matrix}j\kend{matrix}}right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ec347b928cd0f53bde90a10c3bdc6af7b57c266)














![L(n,k) = sum_{j} left[{natop j}right] left{{jatop k}right},](https://wikimedia.org/api/rest_v1/media/math/render/svg/7924bb06e5a919cabfc8bf0410b9501348373f2f)
![{displaystyle left[{n atop j}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d8675a742e1a37b2543d654e9ea87084b66ecd)








