La ley de Snell

Refracciones de luz en la interfaz entre dos medios de diferentes índices refractivos, con n₂ ■ n₁. Puesto que la velocidad es menor en el segundo medio (v₂ c)₁), el ángulo de refracción θ₂ es menos que el ángulo de incidencia θ₁; es decir, el rayo en el medio de índice superior está más cerca de lo normal.

Ley de Snell (también conocida como ley de Snell-Descartes y ley de ibn-Sahl ley y la ley de refracción) es una fórmula utilizada para describir la relación entre los ángulos de incidencia y refracción, cuando se refiere a la luz u otras ondas que pasan a través de un límite entre dos medios isotrópicos diferentes, como el agua, vidrio o aire. Esta ley lleva el nombre del astrónomo y matemático holandés Willebrord Snellius (también llamado Snell).

En óptica, la ley se usa en el trazado de rayos para calcular los ángulos de incidencia o refracción, y en óptica experimental para encontrar el índice de refracción de un material. La ley también se cumple en los metamateriales, que permiten que la luz se doble 'hacia atrás'. en un ángulo de refracción negativo con un índice de refracción negativo.

La ley de Snell establece que, para un par determinado de medios, la relación de los pecados de la incidencia (Silencio Silencio 1{displaystyle theta ¿Qué?) y ángulo de refracción (Silencio Silencio 2{displaystyle theta _{2}) es igual al índice refractivo del segundo medio w.r.t el primero (n₂₁) que es igual a la proporción de los índices refractivos (n₂/n₁) de los dos medios, o equivalentemente, a la relación de las velocidades de fase (v₁/v₂En los dos medios.

pecado⁡ ⁡ Silencio Silencio 1pecado⁡ ⁡ Silencio Silencio 2=n21=n2n1=v1v2{displaystyle {frac {sin theta ################################################################################################################################################################################################################################################################ ¿Qué? {n_{2}{n_{1}}={frac {V_{1} {v_{2}}}}

La ley se deriva del principio de tiempo mínimo de Fermat, que a su vez se deriva de la propagación de la luz como ondas.

Historia

Reproducción de una página del manuscrito de Ibn Sahl mostrando sus diagramas de rayos relacionados con la ley de refracción.

Ptolomeo, en Alejandría, Egipto, había encontrado una relación con respecto a los ángulos de refracción, pero era inexacta para ángulos que no eran pequeños. Ptolomeo confiaba en haber encontrado una ley empírica precisa, en parte como resultado de alterar ligeramente sus datos para que se ajustaran a la teoría (ver: sesgo de confirmación). Alhazen, en su Libro de la Óptica (1021), estuvo más cerca de descubrir la ley de la refracción, aunque no dio este paso.

Una visión de 1837 de la historia de "la ley de los pecados"

El científico persa Ibn Sahl, en la corte de Bagdad en 984, registró diagramas de rayos pero no registró propiedades materiales relacionadas con el índice de refracción, por lo que no puede afirmar haber descubierto la ley de refracción. En el manuscrito On Burning Mirrors and Lenses, Sahl usó diagramas de rayos para derivar formas de lentes que enfocan la luz sin aberraciones geométricas.

La ley fue descubierta por primera vez por Thomas Harriot en 1602, quien sin embargo no publicó sus resultados aunque había mantenido correspondencia con Kepler sobre este mismo tema. En 1621, el astrónomo holandés Willebrord Snellius (1580-1626) —Snell— derivó una forma matemáticamente equivalente, que permaneció inédita durante su vida. René Descartes derivó la ley de forma independiente usando argumentos heurísticos de conservación del momento en términos de senos en su ensayo Dioptrique de 1637, y la usó para resolver una variedad de problemas ópticos. Rechazando a Descartes' Pierre de Fermat llegó a la misma solución basándose únicamente en su principio de tiempo mínimo. Descartes asumió que la velocidad de la luz era infinita, pero en su derivación de la ley de Snell también asumió que cuanto más denso es el medio, mayor es la velocidad de la luz. Fermat apoyó las suposiciones opuestas, es decir, la velocidad de la luz es finita, y su derivación dependía de que la velocidad de la luz fuera más lenta en un medio más denso. La derivación de Fermat también utilizó su invención de la adecuación, un procedimiento matemático equivalente al cálculo diferencial, para encontrar máximos, mínimos y tangentes.

En su influyente libro de matemáticas Geometría, Descartes resuelve un problema en el que trabajaron Apolonio de Perga y Pappo de Alejandría. Dadas n rectas L y un punto P(L) en cada recta, encuentre el lugar geométrico de los puntos Q tales que las longitudes de los segmentos de recta QP(L) satisfagan ciertas condiciones. Por ejemplo, cuando n = 4, dadas las líneas a, b, c y d y un punto A sobre a, B sobre b, y así sucesivamente, encuentre el lugar geométrico de los puntos Q tal que el producto QA*QB es igual al producto QC*QD. Cuando las rectas no son todas paralelas, Pappus demostró que los lugares geométricos son cónicos, pero cuando Descartes consideró n mayor, obtuvo curvas cúbicas y de mayor grado. Para mostrar que las curvas cúbicas eran interesantes, demostró que surgían naturalmente en la óptica a partir de la ley de Snell.

Según Dijksterhuis, "En De natura lucis et proprietate (1662), Isaac Vossius dijo que Descartes había visto el artículo de Snell e inventó su propia prueba. Ahora sabemos que este cargo es inmerecido, pero se ha adoptado muchas veces desde entonces." Tanto Fermat como Huygens repitieron esta acusación de que Descartes había copiado a Snell. En francés, la Ley de Snell se llama "la loi de Descartes" o "loi de Snell-Descartes."

Construcción de Christiaan Huygens

En su Traité de la Lumière de 1678, Christiaan Huygens mostró cómo la ley de los senos de Snell podría explicarse o derivarse de la naturaleza ondulatoria de la luz, usando lo que hemos llegado para llamar el principio de Huygens-Fresnel.

Con el desarrollo de la teoría óptica y electromagnética moderna, la antigua ley de Snell pasó a una nueva etapa. En 1962, Bloembergen demostró que en el límite del medio no lineal, la ley de Snell debe escribirse en forma general. En 2008 y 2011, también se demostró que las metasuperficies plasmónicas cambian las direcciones de reflexión y refracción del haz de luz.

Explicación

La ley de Snell en una pared en Leiden

La ley de Snell se utiliza para determinar la dirección de los rayos de luz a través de medios refractivos con diversos índices de refracción. Los índices de refracción de los medios, etiquetados n1{displaystyle No., n2{displaystyle No. y así sucesivamente, se utilizan para representar el factor por el cual la velocidad de un rayo ligero disminuye cuando viaja a través de un medio refractivo, como el vidrio o el agua, en lugar de su velocidad en un vacío.

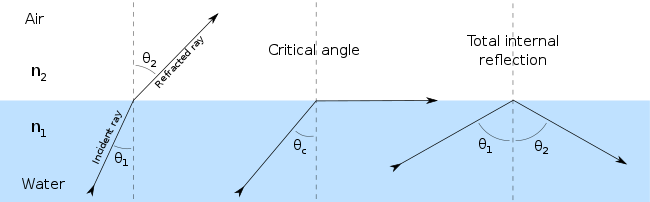
A medida que la luz pasa por el borde entre los medios, según los índices de refracción relativos de los dos medios, la luz se refractará en un ángulo menor o mayor. Estos ángulos se miden con respecto a la línea normal, representada perpendicularmente al límite. En el caso de que la luz viaje del aire al agua, la luz se refractaría hacia la línea normal, porque la luz se ralentiza en el agua; la luz que viaja del agua al aire se refractaría alejándose de la línea normal.

La refracción entre dos superficies también se conoce como reversible porque si todas las condiciones fueran idénticas, los ángulos serían los mismos para la luz que se propaga en la dirección opuesta.

La ley de Snell generalmente se cumple solo para medios isotrópicos o especulares (como el vidrio). En medios anisotrópicos como algunos cristales, la birrefringencia puede dividir el rayo refractado en dos rayos, el rayo ordinario o o que sigue la ley de Snell, y el otro Rayo extraordinario o e que puede no ser coplanar con el rayo incidente.

Cuando la luz u otra onda involucrada es monocromática, es decir, de una sola frecuencia, la ley de Snell también se puede expresar en términos de una relación de longitudes de onda en los dos medios, λ λ 1{displaystyle lambda ¿Qué? y λ λ 2{displaystyle lambda _{2}:

pecado⁡ ⁡ Silencio Silencio 1pecado⁡ ⁡ Silencio Silencio 2=v1v2=λ λ 1λ λ 2{displaystyle {frac {sin theta ################################################################################################################################################################################################################################################################ ¿Qué? {fnK}} {fnK}} {fnMic} {fnK}}} {f}}} {fn}}}} {fn}} {fnMic}}}}}}} {fnf}} {fnK}}}}}}} {fnKf}}}}} {f}}}} {f}}}}}}}}}}}}}}} {f}}}}}}}}}}} {f} {f}} {f} {f} {f}}} {fnf}}}}}}}}}}}}}}} {f} {fnf} {fnf}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {fn {fnMicrode ¿Qué? ¿Qué?

Derivaciones y fórmula

Wavefronts de una fuente puntual en el contexto de la ley de Snell. La región por debajo de la línea gris tiene un índice más alto de refracción, y una velocidad proporcionalmente menor de luz, que la región por encima de ella.

La ley de Snell se puede derivar de varias maneras.

Derivación del principio de Fermat

La ley de Snell se puede derivar del principio de Fermat, que establece que la luz viaja por el camino que tarda menos tiempo. Tomando la derivada de la longitud del camino óptico, se encuentra el punto estacionario que da el camino tomado por la luz. (Hay situaciones en las que la luz viola el principio de Fermat al no tomar el camino de tiempo mínimo, como en el reflejo en un espejo (esférico).) En una analogía clásica, el área de menor índice de refracción se reemplaza por una playa, el zona de mayor índice de refracción junto al mar, y la forma más rápida para que un rescatista en la playa llegue a una persona que se está ahogando en el mar es correr por un camino que siga la ley de Snell.

La luz del medio 1, punto Q, entra en medio 2, la refracción ocurre, y alcanza el punto P finalmente.

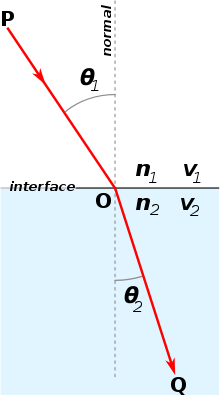
Como se muestra en la figura a la derecha, asuma el índice refractivo del medio 1 y medio 2 son n1{displaystyle No. y n2{displaystyle No. respectivamente. La luz entra en medio 2 del medio 1 por punto O.

Silencio Silencio 1{displaystyle theta ¿Qué? es el ángulo de incidencia, Silencio Silencio 2{displaystyle theta _{2} es el ángulo de refracción respecto a lo normal.

Las velocidades de fase de la luz en el medio 1 y el medio 2 son

v1=c/n1{displaystyle v_{1}=c/n_{1} y

v2=c/n2{displaystyle v_{2}=c/n_{2} respectivamente.

c{displaystyle c} es la velocidad de la luz en vacío.

Sea T el tiempo que tarda la luz en viajar desde el punto Q a través del punto O hasta el punto P.

T=x2+a2v1+b2+()l− − x)2v2=x2+a2v1+b2+l2− − 2lx+x2v2{displaystyle T={frac {sqrt {x^{2}} {v_{1}}}+{frac} {fnK}={2}={2}={2}}={f}= {fnMic} {sqrt {x^{2}+a}{2}}{v_{1}}+{frac} {sqrt {b^{2}+l^{2}-2lx+x^{2}}{v_{2}}}}}}}

donde a, b, l y x son como se indica en la figura de la derecha, siendo x el parámetro variable.

Para minimizarlo, se puede diferenciar:

dTdx=xv1x2+a2+− − ()l− − x)v2()l− − x)2+b2=0{displaystyle {frac {}{dx}={frac} {x}{v_{1}{sqrt [x^{2}+a^{2}}}}}+{frac {-(l-x)}{2}{sqrt {(l-x)}{2}}}}}}=0}} (punto estadístico)

Note que xx2+a2=pecado⁡ ⁡ Silencio Silencio 1{displaystyle {frac {x}{sqrt {x^{2}+a^{2}}}=sin theta ¿Qué?

y l− − x()l− − x)2+b2=pecado⁡ ⁡ Silencio Silencio 2{displaystyle {frac {l-x}{sqrt {(l-x)}{2}+b^{2}}}}=sin theta _{2}

Por lo tanto,

dTdx=pecado⁡ ⁡ Silencio Silencio 1v1− − pecado⁡ ⁡ Silencio Silencio 2v2=0{displaystyle {frac {}{dx}={frac} {sin theta {}{1}{1}} {frac} {sin theta ¿Qué?

pecado⁡ ⁡ Silencio Silencio 1v1=pecado⁡ ⁡ Silencio Silencio 2v2{displaystyle {frac {sin theta {fnK} {fnMicroc} {sin theta ¿Qué?

n1pecado⁡ ⁡ Silencio Silencio 1c=n2pecado⁡ ⁡ Silencio Silencio 2c{displaystyle {frac {fn}sin} theta - ¿Qué? {n_{2}sin theta ¿Qué?

n1pecado⁡ ⁡ Silencio Silencio 1=n2pecado⁡ ⁡ Silencio Silencio 2{displaystyle n_{1}sin theta ¿Por qué?

Derivación del principio de Huygens

Alternativamente, la ley de Snell se puede derivar mediante la interferencia de todos los caminos posibles de la onda de luz desde la fuente hasta el observador; da como resultado una interferencia destructiva en todas partes excepto en los extremos de la fase (donde la interferencia es constructiva), que se convierten en caminos reales.

Derivación de las ecuaciones de Maxwell

Otra forma de derivar la ley de Snell implica la aplicación de las condiciones de contorno generales de las ecuaciones de Maxwell para la inducción y la radiación electromagnética.

Derivación de la conservación de la energía y el momento

Otra manera de derivar la ley de Snell se basa en consideraciones de simetría de traducción. Por ejemplo, una superficie homogénea perpendicular a la dirección z no puede cambiar el impulso transversal. Desde el vector de propagación k→ → {displaystyle {vec}} es proporcional al impulso del fotón, la dirección de propagación transversal ()kx,kSí.,0){displaystyle (k_{x},k_{y},0)} debe permanecer igual en ambas regiones. Suponga sin pérdida de generalidad un plano de incidencia en el z,x{displaystyle z,x} avión kxRegión1=kxRegión2{displaystyle k_{x{text{Region}}_{1}=k_{x{text{Region}}_{2}}}}}. Utilizando la dependencia bien conocida del número de onda sobre el índice refractivo del medio, obtenemos inmediatamente la ley de Snell.

kxRegión1=kxRegión2{displaystyle k_{x{text{Region}}_{1}=k_{x{text{Region}}_{2}},}

n1k0pecado⁡ ⁡ Silencio Silencio 1=n2k0pecado⁡ ⁡ Silencio Silencio 2{displaystyle n_{1}k_{0}sin theta ### {1}=n_{2}k_{0}sin theta _{2},}

n1pecado⁡ ⁡ Silencio Silencio 1=n2pecado⁡ ⁡ Silencio Silencio 2{displaystyle n_{1}sin theta _{1}=n_{2}sin theta _{2},}

Donde k0=2π π λ λ 0=⋅ ⋅ c{displaystyle k_{0}={frac {2pi ♫{lambda ¿Qué? } {c}} es el número de onda en vacío. Aunque ninguna superficie es realmente homogénea a escala atómica, la simetría completa de la traducción es una excelente aproximación cuando la región es homogénea en la escala de la longitud de onda ligera.

Forma vectorial

Dado un vector de luz normalizado l→ → {displaystyle {vec}} (punto desde la fuente de luz hacia la superficie) y un vector normalizado n→ → {displaystyle {vec}}, uno puede resolver los rayos normalizados reflejados y refractados, a través de los cosines del ángulo de incidencia Silencio Silencio 1{displaystyle theta ¿Qué? y ángulo de refracción Silencio Silencio 2{displaystyle theta _{2}, sin utilizar explícitamente los valores sine o cualquier función o ángulo trigonométrico:

#⁡ ⁡ Silencio Silencio 1=− − n→ → ⋅ ⋅ l→ → {displaystyle cos theta ¿Qué? {n}cdot {vec}

Nota: #⁡ ⁡ Silencio Silencio 1{displaystyle cos theta ¿Qué? debe ser positivo, que será si n→ → {displaystyle {vec}} es el vector normal que apunta desde la superficie hacia el lado de donde viene la luz, la región con índice n1{displaystyle No.. Si #⁡ ⁡ Silencio Silencio 1{displaystyle cos theta ¿Qué? es negativo, entonces n→ → {displaystyle {vec}} puntos al lado sin la luz, así que empezar de nuevo con n→ → {displaystyle {vec}} reemplazado por su negativo.

v→ → reflect=l→ → +2#⁡ ⁡ Silencio Silencio 1n→ → {displaystyle {vec {}_{mathrm {reflect}={vec {}}+2cos theta _{1}{vec {n}} {}} {f}}}} {f} {f}}} {f}}}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}} {f}}}}}}}} {f}}} {f}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}} {f}}}}}}}}} {f}}}} {f}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Este vector de dirección reflejado apunta hacia el lado de la superficie de donde provino la luz.

Ahora aplique la ley de Snell a la relación de los senos para obtener la fórmula del vector de dirección del rayo refractado:

pecado⁡ ⁡ Silencio Silencio 2=()n1n2)pecado⁡ ⁡ Silencio Silencio 1=()n1n2)1− − ()#⁡ ⁡ Silencio Silencio 1)2{displaystyle sin theta ¿Qué? {n_{1} {n_{2}}right)sin theta _{1}=left({frac {n_{1}{n_{2}}right){sqrt {1-left(cos theta _{1}right)}}}

#⁡ ⁡ Silencio Silencio 2=1− − ()pecado⁡ ⁡ Silencio Silencio 2)2=1− − ()n1n2)2()1− − ()#⁡ ⁡ Silencio Silencio 1)2){displaystyle cos theta {2}={sqrt {1-(sin theta ¿Por qué? {n_{1} {n_{2}}right)}left(1-left(cos theta _{1}right)} {2}}}}}}}}}

v→ → refract=()n1n2)l→ → +()n1n2#⁡ ⁡ Silencio Silencio 1− − #⁡ ⁡ Silencio Silencio 2)n→ → {displaystyle {vec {}_{mathrm {}=left({frac} {n_{1}{n_{2}}right){vec} {I}+left({frac} {n_{1} {n_{2}}cos theta _{1}-cos theta _{2}right){vec {n}}

La fórmula puede parecer más simple en términos de valores simples renombrados r=n1/n2{displaystyle r=n_{1}/n_{2} y c=− − n→ → ⋅ ⋅ l→ → {displaystyle C=-{vec {n}cdot {vec}, evitando cualquier apariencia de nombres de función de trig o nombres de ángulo:

v→ → refract=rl→ → +()rc− − 1− − r2()1− − c2))n→ → {displaystyle {vec {}_{mathrm {}=r{vec {}}+left(rc-{sqrt {1-r^{2}left(1-c^{2}right)}{vec} {}}}} {derecha){vec {}}}}} {}}}}}}}}}}}}}}} {

Ejemplo:

l→ → ={}0,07107,− − 0,07107},n→ → ={}0,1},r=n1n2=0.9{displaystyle {vec}={0.707107,-0.707107},~{vec {n}={0,1},~r={frac {fn} {}}}=0.9}

c=#⁡ ⁡ Silencio Silencio 1=0,07107,1− − r2()1− − c2)=#⁡ ⁡ Silencio Silencio 2=0,71362{displaystyle c=cos theta _{1}=0.707107,~{sqrt {1-r^{2}left(1-c^{2}right)}=cos theta - ¿Qué?

v→ → reflect={}0,07107,0,07107},v→ → refract={}0.636396,− − 0,71362}{displaystyle {vec {}_{mathrm {reflect}={0.707107,0.707107},~{vec} {V}_{mathrm {refract} }={0.6396,-0.771362}

Los valores del coseno se pueden guardar y utilizar en las ecuaciones de Fresnel para calcular la intensidad de los rayos resultantes.

La reflexión interna total es indicada por una radicand negativa en la ecuación para #⁡ ⁡ Silencio Silencio 2{displaystyle cos theta ¿Qué?, que sólo puede suceder para los rayos que cruzan en un medio menos condensado (<math alttext="{displaystyle n_{2}n2.n1{displaystyle No.<img alt=" n_2 ).

Reflexión interna total y ángulo crítico

Demostración de no refracción en ángulos superiores al ángulo crítico.

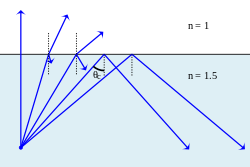
Cuando la luz viaja de un medio con un índice de refracción más alto a uno con un índice de refracción más bajo, la ley de Snell parece requerir en algunos casos (siempre que el ángulo de incidencia sea lo suficientemente grande) que el seno del ángulo de refracción sea mayor que uno. Por supuesto, esto es imposible, y la luz en tales casos se refleja completamente en el límite, un fenómeno conocido como reflexión interna total. El ángulo de incidencia más grande posible que todavía da como resultado un rayo refractado se denomina ángulo crítico; en este caso, el rayo refractado viaja a lo largo del límite entre los dos medios.

Refraction of light at the interface between two media.

Por ejemplo, considere un rayo de luz que se mueve del agua al aire con un ángulo de incidencia de 50°. Los índices de refracción del agua y el aire son aproximadamente 1,333 y 1, respectivamente, por lo que la ley de Snell nos da la relación

pecado⁡ ⁡ Silencio Silencio 2=n1n2pecado⁡ ⁡ Silencio Silencio 1=1.3331⋅ ⋅ pecado⁡ ⁡ ()50∘ ∘ )=1.333⋅ ⋅ 0.766=1.021,{displaystyle sin theta ¿Qué? {n_{1} {n_{2}}sin} theta _{1}={frac {1.333}{1}cdot sin left(50^{circ }right)=1.333cdot 0.766=1.021,}

que es imposible de satisfacer. El ángulo crítico θ_crit es el valor de θ₁ para el cual θ₂ es igual a 90°:

Silencio Silencio crit=arcsin⁡ ⁡ ()n2n1pecado⁡ ⁡ Silencio Silencio 2)=arcsin⁡ ⁡ n2n1=48.6∘ ∘ .{displaystyle theta _{text{crit}}=arcsin left({frac {n_{2} {n_{1}}}sin theta _{2}right)=arcsin {fracsin}fracsin theta {fn} {fn}}=48.6}{c} {fn} {fn} {fn}}}}} {fn_}}}}}} {fn} {fn}}}}}} {fn}}}}}}}}}}}}} {fn_}}}}}}}}}}}} {\4\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} }

Dispersión

En muchos medios de propagación de ondas, la velocidad de las ondas cambia con la frecuencia o la longitud de onda de las ondas; esto es cierto para la propagación de la luz en la mayoría de las sustancias transparentes que no sean el vacío. Estos medios se denominan dispersivos. El resultado es que los ángulos determinados por la ley de Snell también dependen de la frecuencia o la longitud de onda, por lo que un rayo de longitudes de onda mixtas, como la luz blanca, se propagará o dispersará. Tal dispersión de la luz en el vidrio o el agua subyace en el origen de los arco iris y otros fenómenos ópticos, en los que las diferentes longitudes de onda aparecen como diferentes colores.

En los instrumentos ópticos, la dispersión conduce a la aberración cromática; una borrosidad dependiente del color que a veces es el efecto que limita la resolución. Esto era especialmente cierto en los telescopios de refracción, antes de la invención de los objetivos acromáticos.

Medios con pérdidas, absorbentes o conductores

En un medio conductor, la permitividad y el índice de refracción tienen valores complejos. En consecuencia, también lo son el ángulo de refracción y el vector de onda. Esto implica que, mientras que las superficies de fase real constante son planos cuyas normales forman un ángulo igual al ángulo de refracción con la interfase normal, las superficies de amplitud constante, en cambio, son planos paralelos a la interfase misma. Dado que estos dos planos en general no coinciden entre sí, se dice que la onda no es homogénea. La onda refractada se atenúa exponencialmente, con exponente proporcional a la componente imaginaria del índice de refracción.