La ley de Amdahl

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Fórmula en arquitectura informática

La velocidad teórica de la latencia (a través de una reducción de latencia, es decir: latencia como métrica es el tiempo transcurrido entre una entrada y salida en un sistema) de la ejecución de un programa como función del número de procesadores que lo ejecutan, de acuerdo con la ley de Amdahl. La velocidad es limitada por la parte serie del programa. Por ejemplo, si el 95% del programa se puede paralizar, la velocidad máxima teórica usando el cálculo paralelo sería 20 veces.

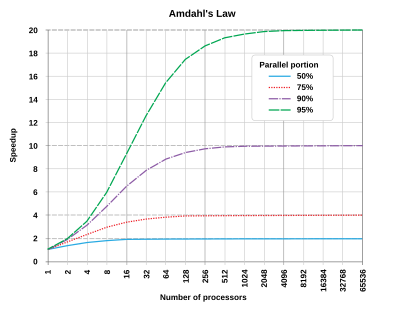
En arquitectura informática, la ley de Amdahl (o argumento de Amdahl) es una fórmula que proporciona la aceleración teórica en latencia de la ejecución de una tarea con una carga de trabajo fija que se puede esperar de un sistema cuyos recursos se han mejorado. Establece que "la mejora general del rendimiento obtenida mediante la optimización de una sola parte de un sistema está limitada por la fracción de tiempo en que se usa realmente la parte mejorada". Lleva el nombre del científico informático Gene Amdahl y se presentó en la Conferencia informática conjunta de primavera de la Federación Estadounidense de Sociedades de Procesamiento de la Información (AFIPS) en 1967.

La ley de Amdahl se utiliza a menudo en computación paralela para predecir la velocidad teórica al usar múltiples procesadores. Por ejemplo, si un programa necesita 20 horas para completar el uso de un solo hilo, pero una porción de una hora del programa no puede ser paralizada, por lo tanto sólo las 19 horas restantes" (p = 0,95) tiempo de ejecución se puede paralizar, entonces independientemente de cuántos hilos se dedican a una ejecución paralela de este programa, el tiempo mínimo de ejecución no puede ser menos de una hora. Por lo tanto, la velocidad teórica se limita a la mayoría de 20 veces el rendimiento del hilo único, ${displaystyle left({dfrac {1}{1-p}}=20right)}$ .

Definición

La ley de Amdahl se puede formular de la siguiente manera:

{displaystyle S_{text{latency}}(s)={frac {1}{(1-p)+{frac {p}{s}}}}}

dónde

S_latencia es la aceleración teórica de la ejecución de toda la tarea;
s es la aceleración de la parte de la tarea que se beneficia de la mejora de los recursos del sistema;
p es la proporción del tiempo de ejecución que la parte que se beneficia de mejores recursos originalmente ocupados.

Además,

{displaystyle {begin{cases}S_{text{latency}}(s)leq {dfrac {1}{1-p}}\[8pt]lim limits _{sto infty }S_{text{latency}}(s)={dfrac {1}{1-p}}.end{cases}}}

muestra que la aceleración teórica de la ejecución de toda la tarea aumenta con la mejora de los recursos del sistema y que, independientemente de la magnitud de la mejora, la aceleración teórica siempre está limitada por la parte de la tarea que no puede beneficiarse de la mejora.

La ley de Amdahl se aplica solo a los casos en los que el tamaño del problema es fijo. En la práctica, a medida que hay más recursos informáticos disponibles, tienden a usarse en problemas más grandes (conjuntos de datos más grandes), y el tiempo dedicado a la parte paralelizable a menudo crece mucho más rápido que el trabajo inherentemente en serie. En este caso, la ley de Gustafson da una evaluación menos pesimista y más realista del desempeño paralelo.

Derivación

Una tarea ejecutada por un sistema cuyos recursos son mejorados en comparación con un sistema similar inicial se puede dividir en dos partes:

a part that does not benefit from the improvement of the resources of the system;
una parte que se beneficia de la mejora de los recursos del sistema.

Un ejemplo es un programa de computadora que procesa archivos. Una parte de ese programa puede escanear el directorio del disco y crear una lista de archivos internamente en la memoria. Después de eso, otra parte del programa pasa cada archivo a un subproceso separado para su procesamiento. La parte que escanea el directorio y crea la lista de archivos no se puede acelerar en una computadora paralela, pero la parte que procesa los archivos sí.

El tiempo de ejecución de toda la tarea antes de la mejora de los recursos del sistema se denota como $T$ . Incluye el tiempo de ejecución de la parte que no se beneficiaría de la mejora de los recursos y el tiempo de ejecución del que se beneficiaría de ella. La fracción del tiempo de ejecución de la tarea que se beneficiaría de la mejora de los recursos se denota por $p$ . Por lo tanto, el que se refiere a la parte que no se beneficiaría de ella es ${displaystyle 1-p}$ . Entonces:

T=(1-p)T+pT.

Es la ejecución de la parte que se beneficia de la mejora de los recursos que se acelera por el factor $s$ después de la mejora de los recursos. En consecuencia, el tiempo de ejecución de la parte que no se beneficia de ella sigue siendo el mismo, mientras que la parte que se beneficia de ella se convierte en:

{frac {p}{s}}T.

El tiempo de ejecución teórica ${displaystyle T(s)}$ de toda la tarea después de la mejora de los recursos es entonces:

{displaystyle T(s)=(1-p)T+{frac {p}{s}}T.}

La ley de Amdahl da la velocidad teórica de la latencia de la ejecución de toda la tarea volumen fijo $W$ , que rinde

{displaystyle S_{text{latency}}(s)={frac {TW}{T(s)W}}={frac {T}{T(s)}}={frac {1}{1-p+{frac {p}{s}}}}.}

Programas paralelos

Si el 30% del tiempo de ejecución puede ser objeto de una aceleración, p será 0,3; si la mejora hace que la parte afectada sea dos veces más rápida, s será 2. La ley de Amdahl establece que la aceleración general de la aplicación de la mejora será:

{displaystyle S_{text{latency}}={frac {1}{1-p+{frac {p}{s}}}}={frac {1}{1-0.3+{frac {0.3}{2}}}}=1.18.}

Por ejemplo, supongamos que se nos asigna una tarea en serie que se divide en cuatro partes consecutivas, cuyos porcentajes de tiempo de ejecución son p1 = 0,11, p2 = 0,18, p3 = 0,23, y p4 = 0,48 respectivamente. Luego se nos dice que la primera parte no se acelera, entonces s1 = 1, mientras que la segunda parte se acelera 5 veces, entonces s2 = 5, la tercera parte se acelera 20 veces, entonces s3 = 20, y la cuarta parte se acelera 1,6 veces, por lo que s4 = 1,6. Al usar la ley de Amdahl, la aceleración general es

S_{text{latency}}={frac {1}{{frac {p1}{s1}}+{frac {p2}{s2}}+{frac {p3}{s3}}+{frac {p4}{s4}}}}={frac {1}{{frac {0.11}{1}}+{frac {0.18}{5}}+{frac {0.23}{20}}+{frac {0.48}{1.6}}}}=2.19.

Observe cómo la aceleración de 5 y 20 veces en la segunda y tercera parte respectivamente no tiene mucho efecto en la aceleración general cuando la cuarta parte (48 % del tiempo de ejecución) se acelera solo 1,6 veces.

Programas de serie

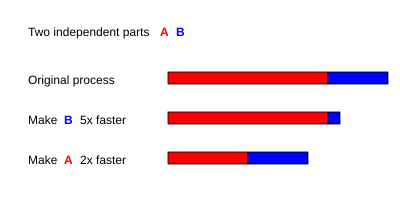
Supongamos que una tarea tiene dos partes independientes, A y B. Parte B toma aproximadamente el 25% del tiempo de la computación entera. Al trabajar muy duro, uno puede ser capaz de hacer esta parte 5 veces más rápido, pero esto reduce el tiempo de toda la computación sólo ligeramente. En cambio, es posible que necesite realizar menos trabajo para hacer parte A actuar dos veces más rápido. Esto hará que el cálculo sea mucho más rápido que mediante la optimización de la parte B, aunque parte B 's velocidad es mayor en términos de la relación, (5 veces contra 2 veces).

Por ejemplo, con un programa serial en dos partes A y B para el cual T<sub A = 3 s y T_B = 1 segundo,

si parte B está hecho para correr 5 veces más rápido, eso es s = 5 y p = T_B/(T_A + T_B) = 0,25, entonces

{displaystyle S_{text{latency}}={frac {1}{1-0.25+{frac {0.25}{5}}}}=1.25;}

si parte A está hecho para correr 2 veces más rápido, eso es s = 2 y p = T_A/(T_A + T_B) = 0,75, entonces

{displaystyle S_{text{latency}}={frac {1}{1-0.75+{frac {0.75}{2}}}}=1.60.}

Por lo tanto, hacer que la parte A se ejecute 2 veces más rápido es mejor que hacer que la parte B se ejecute 5 veces más rápido. El porcentaje de mejora en la velocidad se puede calcular como

{displaystyle {text{percentage improvement}}=100left(1-{frac {1}{S_{text{latency}}}}right).}

Mejora de la parte A por un factor de 2 aumentará la velocidad global del programa por un factor de 1.60, lo que lo hace 37,5% más rápido que el cálculo original.
Sin embargo, mejorar la parte B por un factor de 5, que presumiblemente requiere más esfuerzo, logrará un factor de aceleración global de 1,25 solamente, lo que lo hace 20% más rápido.

Optimización de la parte secuencial de programas paralelos

Si la parte no paralelizante es optimizada por un factor $O$ , entonces

{displaystyle T(O,s)=(1-p){frac {T}{O}}+{frac {p}{s}}T.}

De la ley de Amdahl se deduce que la aceleración debida al paralelismo está dada por

{displaystyle S_{text{latency}}(O,s)={frac {T(O)}{T(O,s)}}={frac {(1-p){frac {1}{O}}+{p}}{{frac {1-p}{O}}+{frac {p}{s}}}}.}

Cuando $s=1$ , tenemos ${displaystyle S_{text{latency}}(O,s)=1}$ , significa que la velocidad es medido con respecto al tiempo de ejecución después de que la parte no parallelizable sea optimizada.

Cuando $s=infty$ ,

{displaystyle S_{text{latency}}(O,infty)={frac {T(O)}{T(O,s)}}={frac {(1-p){frac {1}{O}}+{p}}{{frac {1-p}{O}}+{frac {p}{s}}}}=1+{frac {p}{1-p}}O.}

Si ${displaystyle 1-p=0.4}$ , ${displaystyle O=2}$ y $s=5$ , entonces:

{displaystyle S_{text{latency}}(O,s)={frac {T(O)}{T(O,s)}}={frac {{0.4}{frac {1}{2}}+0.6}{{frac {0.4}{2}}+{frac {0.6}{5}}}}=2.5.}

Transformar partes secuenciales de programas paralelos en paralelizables

A continuación, consideramos el caso en el que la parte no paralelable se reduce por un factor de ${displaystyle O'}$ , y la parte paralelizable se aumenta correspondientemente. Entonces...

{displaystyle T'(O',s)={frac {1-p}{O'}}T+left(1-{frac {1-p}{O'}}right){frac {T}{s}}.}

De la ley de Amdahl se deduce que la aceleración debida al paralelismo está dada por

{displaystyle S'_{text{latency}}(O',s)={frac {T'(O')}{T'(O',s)}}={frac {1}{{frac {1-p}{O'}}+left(1-{frac {1-p}{O'}}right){frac {1}{s}}}}.}

La derivación anterior está de acuerdo con el análisis de Jakob Jenkov del equilibrio entre el tiempo de ejecución y la aceleración.

Relación con la ley de rendimientos decrecientes

La ley de Amdahl a menudo se combina con la ley de rendimientos decrecientes, mientras que solo un caso especial de aplicación de la ley de Amdahl demuestra la ley de rendimientos decrecientes. Si uno elige de manera óptima (en términos de la aceleración lograda) lo que se debe mejorar, entonces verá mejoras monótonamente decrecientes a medida que mejora. Sin embargo, si uno elige de manera no óptima, después de mejorar un componente subóptimo y pasar a mejorar un componente más óptimo, puede ver un aumento en el rendimiento. Tenga en cuenta que a menudo es racional mejorar un sistema en un orden que es "no óptimo" en este sentido, dado que algunas mejoras son más difíciles o requieren mayor tiempo de desarrollo que otras.

La ley de Amdahl representa la ley de rendimientos decrecientes si uno está considerando qué tipo de rendimiento obtiene al agregar más procesadores a una máquina, si está ejecutando un cálculo de tamaño fijo que usará todos los procesadores disponibles para su capacidad. Cada nuevo procesador agregado al sistema agregará menos energía utilizable que el anterior. Cada vez que se duplique la cantidad de procesadores, la tasa de aceleración disminuirá, ya que el rendimiento total se acercará al límite de 1/(1 − p).

Este análisis ignora otros posibles cuellos de botella, como el ancho de banda de la memoria y el ancho de banda de E/S. Si estos recursos no escalan con la cantidad de procesadores, simplemente agregar procesadores proporciona rendimientos aún más bajos.

Una implicación de la ley de Amdahl es que para acelerar las aplicaciones reales que tienen partes tanto en serie como en paralelo, se requieren técnicas de computación heterogéneas. Hay nuevos modelos de aceleración y consumo de energía basados en una representación más general de la heterogeneidad, denominada heterogeneidad de forma normal, que admiten una amplia gama de arquitecturas heterogéneas de muchos núcleos. Estos métodos de modelado tienen como objetivo predecir la eficiencia energética del sistema y los rangos de rendimiento, y facilitan la investigación y el desarrollo a nivel de hardware y software del sistema.

Contenido relacionado

Más resultados...