La elasticidad precio de la demanda

Una buena elasticidad del precio de la demanda ()Ed{displaystyle E_{d}, PED) es una medida de lo sensible que la cantidad demandada es a su precio. Cuando el precio aumenta, la cantidad demandada cae por casi cualquier bien, pero cae más para algunos que para otros. La elasticidad del precio da el cambio porcentual en la cantidad demandada cuando hay un aumento por ciento en el precio, manteniendo todo lo demás constante. Si la elasticidad es -2, eso significa que un aumento del precio del uno por ciento conduce a una disminución del dos por ciento en la cantidad demandada. Otras elasticidades miden cómo la cantidad demandada cambios con otras variables (por ejemplo, la elasticidad de los ingresos de la demanda de cambios de ingresos del consumidor).

Las elasticidades precio son negativas excepto en casos especiales. Si se dice que un bien tiene una elasticidad de 2, casi siempre significa que el bien tiene una elasticidad de −2 según la definición formal. La frase "más elástica" significa que la elasticidad de un bien tiene mayor magnitud, ignorando el signo. Los bienes de Veblen y Giffen son dos clases de bienes que tienen elasticidad positiva, raras excepciones a la ley de la demanda. Se dice que la demanda de un bien es inelástica cuando la elasticidad es menor que uno en valor absoluto: es decir, los cambios en el precio tienen un efecto relativamente pequeño sobre la cantidad demandada. Se dice que la demanda de un bien es elástica cuando la elasticidad es mayor que uno. Un bien con una elasticidad de −2 tiene una demanda elástica porque la cantidad cae el doble que el aumento del precio; una elasticidad de -0,5 tiene una demanda inelástica porque la respuesta cuantitativa es la mitad del aumento de precio.

Con una elasticidad de 0, el consumo no cambiaría en absoluto, a pesar de los aumentos de precios.

Los ingresos se maximizan cuando el precio se establece de modo que la elasticidad sea exactamente uno. La elasticidad del bien se puede utilizar para predecir la incidencia (o 'carga') de un impuesto sobre ese bien. Se utilizan varios métodos de investigación para determinar la elasticidad de los precios, incluidos mercados de prueba, análisis de datos históricos de ventas y análisis conjunto.

Definición

La variación de la demanda en respuesta a una variación del precio se denomina elasticidad precio de la demanda. También se puede definir como la relación entre el cambio porcentual en la cantidad demandada y el cambio porcentual en el precio de un bien en particular. La formula pues el coeficiente de elasticidad precio de la demanda de un bien es:

E.. p.. =Δ Δ Q/QΔ Δ P/P{displaystyle E_{langle prangle }={frac {Delta Q/Q}{Delta P/P}}

Donde P{displaystyle P} es el precio inicial del bien demandado, Δ Δ P{displaystyle Delta P} es cuánto cambió, Q{displaystyle Q} es la cantidad inicial del bien demandado, y Δ Δ Q{displaystyle Delta Q} es lo mucho que cambió. En otras palabras, podemos decir que la elasticidad del precio de la demanda es el cambio porcentual de la demanda de una mercancía debido a un cambio porcentual determinado en el precio. Si la cantidad demandada cae 20 toneladas de una inicial 200 toneladas después de que el precio aumente $5 de un precio inicial de $100, entonces la cantidad demandada ha caído 10% y el precio ha aumentado 5%, por lo que la elasticidad es (−10%)/(+5%) = −2.

La elasticidad precio de la demanda normalmente es negativa porque la cantidad demandada cae cuando el precio sube, como se describe en la "ley de la demanda". Dos clases raras de bienes que tienen una elasticidad mayor que 0 (los consumidores compran más si el precio es más alto) son los bienes Veblen y Giffen. Dado que la elasticidad precio de la demanda es negativa para la gran mayoría de los bienes y servicios (a diferencia de la mayoría de las otras elasticidades, que toman valores tanto positivos como negativos según el bien), los economistas suelen omitir la palabra "negativa"; o el signo menos y se refieren a la elasticidad precio de la demanda como un valor positivo (es decir, en términos de valor absoluto). Dirán "Los yates tienen una elasticidad de dos" lo que significa que la elasticidad es −2. Esta es una fuente común de confusión para los estudiantes.

Dependiendo de su elasticidad, se dice que un bien tiene demanda elástica 1), demanda inelástica (aplicada 1), o demanda elástica unitaria (= 1). Si la demanda es elástica, la cantidad demandada es muy sensible al precio, por ejemplo cuando un aumento del 1% en el precio genera una disminución del 10% en la cantidad. Si la demanda es inelástica, la demanda del bien es relativamente insensible al precio, con la cantidad que cambia menos que el precio. Si la demanda es elástica unitaria, la cantidad cae exactamente en el porcentaje que el precio aumenta. Dos casos especiales importantes son la demanda perfectamente elástica (= ∞), donde incluso un pequeño aumento de precio reduce la cantidad demandada a cero; y la demanda perfectamente inelástica (= 0), donde un aumento de precio deja la cantidad sin cambios. La medida anterior de elasticidad se conoce a veces como la precio propio elasticidad de la demanda de un bien, es decir, la elasticidad de la demanda con respecto al propio precio del bien, para distinguirlo de la elasticidad de la demanda de ese bien con respecto al cambio en el precio de otro bien, es decir, un bien independiente, complementario o sustituto. Ese tipo de elasticidad de dos buenos se llama elasticidad de precio cruzado de la demanda. Si un aumento del 1% en el precio de la gasolina causa una caída del 0,5% en la cantidad de coches demandados, la elasticidad de precio cruzado es Ecgd=()− − 0.5% % )/()+1% % )=− − 0,5.{displaystyle E_{cg}=(-0.5%)/(+1%)=-0.5}

A medida que el tamaño del cambio de precio se hace más grande, la definición de elasticidad se vuelve menos confiable por una combinación de dos razones. En primer lugar, la elasticidad de un bien no es necesariamente constante; varía en diferentes puntos a lo largo de la curva de demanda porque un cambio de 1% en el precio tiene un efecto de cantidad que puede depender de si el precio inicial es alto o bajo. Contrariamente a la concepción errónea común, la elasticidad del precio no es constante incluso a lo largo de una curva de demanda lineal, sino que varía a lo largo de la curva. Una pendiente de curva de demanda lineal es constante, para estar seguro, pero la elasticidad puede cambiar incluso si Δ Δ P/Δ Δ Q{displaystyle Delta P/Delta Q} es constante. Existe una forma no lineal de curva de demanda a lo largo de la cual la elasticidad es constante: P=aQ1/E{displaystyle P=aQ^{1/E}, donde a{displaystyle a} es un cambio constante y E{displaystyle E} es la elasticidad.

En segundo lugar, los cambios porcentuales no son simétricos; en cambio, el cambio porcentual entre dos valores depende del cual uno es elegido como valor inicial y que como valor final. Por ejemplo, supongamos que cuando el precio se eleva de $10 a $16, la cantidad cae de 100 unidades a 80. Se trata de un aumento del precio del 60% y una disminución de la cantidad del 20%, una elasticidad ()− − 20% % )/()+60% % ).. − − 0.33{displaystyle (-20%)/(+60%)approx -0.33} para esa parte de la curva de demanda. Si el precio baja de $16 a $10 y la cantidad aumenta de 80 unidades a 100, sin embargo, el descenso del precio es 37,5% y el aumento de la cantidad es 25%, una elasticidad de ()+25% % )/()− − 37,5% % )=− − 0,677{displaystyle (+25%)/(-37.5%)=-0.67} por la misma parte de la curva. Este es un ejemplo del problema del número de índice.

Se utilizan dos refinamientos de la definición de elasticidad para tratar estas deficiencias de la fórmula básica de elasticidad: elasticidad de arco y elasticidad puntual.

La elasticidad del arco

La elasticidad del arco fue introducida muy pronto por Hugh Dalton. Es muy similar a un problema ordinario de elasticidad, pero agrega el problema del número índice. Arc Elasticity es una segunda solución al problema de asimetría de tener una elasticidad que depende de cuál de los dos puntos dados en una curva de demanda se elige como el "original" punto voluntad y que como el "nuevo" una es calcular el cambio porcentual en P y Q en relación con el promedio de los dos precios y el promedio de las dos cantidades, en lugar de solo el cambio relativo a un punto o el otro. En términos generales, esto da un "promedio" elasticidad para la sección de la curva de demanda real, es decir, el arco de la curva, entre los dos puntos. En consecuencia, esta medida se conoce como elasticidad arco, en este caso con respecto al precio del bien. La elasticidad del arco se define matemáticamente como:

Ed=P1+P22Qd1+Qd22× × Δ Δ QdΔ Δ P=P1+P2Qd1+Qd2× × Δ Δ QdΔ Δ P{displaystyle E_{d}={frac {frac {fnMicroc} {fnMicroc}} {fnMicroc}} {fnK}}} {fn}}} {fn}}} {fn}}}} {fnK}} {fn}}}}}}} {f}}}}}}} {fnMicroc} {f}}}}}} {f}}}}}}}}}}}}}}} {f}}}}} {f}}}} {f}}}} {f} {f} {f} {f}}f}f}}}}f}f}f}}f} {f} {f} {f} {f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft} {fnMicroc} {fnMicroc} {\fnMicrosoft} {fnMicroc} {fnMicroc} {fnMicroc {fnMicroc} {fnMicroc {f}fnMicroc}} {fnMicroc}} {f}}}}}}}}}}}}} {\f}f}f}f}f}f}f}f}f}f}f}f}fnf}fnf}f}fnf}fnfnfn}fn}f}fn}\fn\\\fnfnfnfn}fnfnfnMicrocfnMicroc}fnMicroc}\fnMicroc}\fn Delta P}={frac {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft} {fnMicroc} {fnMicroc} {\fnMicrosoft} {fnMicroc} {fnMicroc} {fnMicroc {fnMicroc} {fnMicroc {f}fnMicroc}} {fnMicroc}} {f}}}}}}}}}}}}} {\f}f}f}f}f}f}f}f}f}f}f}f}fnf}fnf}f}fnf}fnfnfn}fn}f}fn}\fn\\\fnfnfnfn}fnfnfnMicrocfnMicroc}fnMicroc}\fnMicroc}\fn Delta P}

Este método para calcular la elasticidad del precio también se conoce como la "fórmula de los puntos medios", porque el precio promedio y la cantidad promedio son las coordenadas del punto medio de la línea recta entre los dos puntos dados. Esta fórmula es una aplicación del método del punto medio. Sin embargo, debido a que esta fórmula asume implícitamente que la sección de la curva de demanda entre esos puntos es lineal, cuanto mayor sea la curvatura de la curva de demanda real en ese rango, peor será esta aproximación de su elasticidad.

Elasticidad del punto

El método de la elasticidad puntual de la demanda se utiliza para determinar el cambio en la demanda dentro de la misma curva de demanda; básicamente, una cantidad muy pequeña de cambio en la demanda se mide a través de la elasticidad puntual. Una forma de evitar el problema de precisión descrito anteriormente es minimizar la diferencia entre los precios y las cantidades iniciales y finales. Este es el enfoque adoptado en la definición de elasticidad puntual, que utiliza cálculo diferencial para calcular la elasticidad de un cambio infinitesimal en el precio y la cantidad en cualquier punto dado de la curva de demanda:

Ed=dQddP× × PQd{displaystyle E_{d}={frac {mhm} Q_{d}{mathrm {}times {frac {fnK}}

En otras palabras, es igual al valor absoluto del primer derivado de la cantidad con respecto al precio dQddP{displaystyle {frac {mathrm}{d}{}{mathrm {d}} {}}}} {}}}} {f}}}}} {f}}}}} {f}}}}} {f}}}} multiplicado por el precio del punto (P) dividido por su cantidad (Q_d). Sin embargo, la elasticidad del punto se puede calcular sólo si la fórmula para la función de demanda, Qd=f()P){displaystyle Q_{d}=f(P)}, se conoce así su derivado con respecto al precio, dQd/dP{displaystyle {dQ_{d}/dP}, se puede determinar.

En términos de cálculo parcial-diferencial, la elasticidad del punto de la demanda se puede definir como sigue: x()p,w){displaystyle displaystyle x(p,w)} ser la demanda de bienes x1,x2,...... ,xL{displaystyle x_{1},x_{2},dotsx_{L} como función del precio de los parámetros y la riqueza, y dejar xl l ()p,w){displaystyle displaystyle x_{ell }(p,w)} ser la demanda del bien l l {displaystyle displaystyle ell }. La elasticidad de la demanda para el bien xl l ()p,w){displaystyle displaystyle x_{ell }(p,w)} con respecto al precio pk{displaystyle P_{k} es

Exl l ,pk=∂ ∂ xl l ()p,w)∂ ∂ pk⋅ ⋅ pkxl l ()p,w)=∂ ∂ log⁡ ⁡ xl l ()p,w)∂ ∂ log⁡ ⁡ pk{displaystyle E_{x_{ell ¿Qué? {fnK}{x_{ell } {fnMicroc {partial log x_{ell } {p,w)}{partiallog p_{k}}}}}} {fnMicrosoft} {fnK}}}} {fnK}}}}} {cH0}}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}} {pppppppppppppppppppppcccccccccccccccH00ccH00ccH00ccH00cH00cH00cH00ccccH00ccH00}}}}}}}}}

Historia

La ilustración que acompañaba la definición original de elasticidad de Marshall, la relación de PT a Pt

Junto con el concepto de una "elasticidad" económica; coeficiente, a Alfred Marshall se le atribuye la definición de "elasticidad de la demanda" en Principles of Economics, publicado en 1890. Alfred Marshall inventó la elasticidad precio de la demanda solo cuatro años después de haber inventado el concepto de elasticidad. Usó la creación básica de Cournot de la curva de demanda para obtener la ecuación de la elasticidad precio de la demanda. Describió la elasticidad precio de la demanda así: "Y podemos decir en general: la elasticidad (o capacidad de respuesta) de la demanda en un mercado es grande o pequeña según la cantidad demandada aumente mucho o poco para una caída dada en el precio"., y disminuye mucho o poco para un aumento dado en el precio. Él razona esto ya que "la única ley universal en cuanto al deseo de una persona por una mercancía es que disminuye... pero esta disminución puede ser lenta o rápida". Si es lento... una pequeña caída en el precio provocará un aumento comparativamente grande en sus compras. Pero si es rápido, una pequeña caída en el precio provocará sólo un aumento muy pequeño en sus compras. En el primer caso... la elasticidad de sus deseos, podemos decir, es grande. En el último caso... la elasticidad de su demanda es pequeña." Matemáticamente, el PED marshalliano se basó en una definición de precio puntual, utilizando cálculo diferencial para calcular elasticidades.

Determinantes

El factor primordial para determinar la elasticidad es la voluntad y la capacidad de los consumidores después de un cambio de precio para posponer las decisiones de consumo inmediatas relacionadas con el bien y buscar sustitutos ("esperar y mirar"). Por lo tanto, varios factores pueden afectar la elasticidad de la demanda de un bien:

Disponibilidad de bienes sustitutivos

Cuanto más y más cerca estén los sustitutos disponibles, mayor será la elasticidad, ya que la gente puede cambiar fácilmente de un bien a otro si se hace un cambio de precio menor; Hay un fuerte efecto de sustitución. Si no hay sustitutos cercanos disponibles, el efecto de sustitución será pequeño y la demanda inelástica.

La amplitud de la definición de un bien

Cuanto más amplia es la definición de un bien (o servicio), menor es la elasticidad. Por ejemplo, los peces y chips de la Compañía X tienden a tener una elasticidad relativamente alta de la demanda si hay un número significativo de sustitutos disponibles, mientras que los alimentos en general tendrían una elasticidad extremadamente baja de la demanda porque no existen sustitutos. Los productos alimenticios específicos (crema de hielo, carne, espinacas) o las familias de ellos (carne, carne, productos marinos) pueden ser más elásticos.

Porcentaje de ingresos

Cuanto mayor sea el porcentaje de ingresos del consumidor que representa el precio del producto, mayor será la elasticidad, ya que la gente prestará más atención al comprar el bien debido a su costo; El efecto de ingreso es sustancial. Cuando las mercancías representan sólo una parte insignificante del presupuesto, el efecto de los ingresos será insignificante y exigirá inelástico,

Necesidad

Cuanto más necesario es un bien, menor es la elasticidad, ya que la gente intentará comprarlo sin importar el precio, como el caso de la insulina para aquellos que lo necesitan.

Duración

Para la mayoría de los bienes, cuanto más tiempo tenga un cambio de precio, más alta será la elasticidad, ya que cada vez más consumidores encuentran que tienen el tiempo y la inclinación para buscar sustitutos. Cuando los precios del combustible aumentan repentinamente, por ejemplo, los consumidores todavía pueden llenar sus tanques vacíos a corto plazo, pero cuando los precios permanecen altos durante varios años, más consumidores reducirán su demanda de combustible cambiando a carpooling o transporte público, invirtiendo en vehículos con mayor economía de combustible o tomando otras medidas. Sin embargo, esto no se mantiene para las duraderas del consumidor como los propios coches; eventualmente, puede ser necesario que los consumidores reemplacen sus coches actuales, por lo que uno esperaría que la demanda sea menos elástica.

Lealtad de marca

Un apego a una determinada marca —ya fuera de la tradición o debido a barreras propias— puede anular la sensibilidad a los cambios de precios, lo que resulta en una demanda más inelástica.

Quien paga

Cuando el comprador no paga directamente el bien que consume, como con cuentas de gastos corporativos, es probable que la demanda sea más inelástica.

Adicción

Los bienes que son más adictivos por naturaleza tienden a tener un PED inelástico (valor absoluto de PED < 1). Ejemplos de tales incluyen cigarrillos, heroína y alcohol. Esto se debe a que los consumidores tratan dichos bienes como necesidades y, por lo tanto, se ven obligados a comprarlos, incluso a pesar de cambios significativos en los precios.

Relación con el ingreso marginal

La siguiente ecuación se cumple:

R.=P()1+1Ed){displaystyle R'=P,left(1+{dfrac {1} {E_{d}}}derecha)}

dónde

R′ es el ingreso marginal

P es el precio

Prueba:

Definir los ingresos totales R

R.=∂ ∂ R∂ ∂ Q=∂ ∂ ∂ ∂ Q()PQ)=P+Q∂ ∂ P∂ ∂ Q{displaystyle R'={frac {partial R}{partial Q}={frac {partial }{partial Q}(P,Q)=P+Q,{frac {partial P}{partial P}{partial Q}

Ed=∂ ∂ Q∂ ∂ P⋅ ⋅ PQ⇒ ⇒ Ed⋅ ⋅ QP=∂ ∂ Q∂ ∂ P⇒ ⇒ PEd⋅ ⋅ Q=∂ ∂ P∂ ∂ Q{displaystyle E_{d}={dfrac {partial Q}{partial P} 'cdot {dfrac {fnK}fnK}cdot {fnMicroc} {fnK}= {fnMicroc {fnMicrosoft} {fnMicrosoft} {f} {f} {f}} {f}} {f}} {f}}} {f} {f} {f}} {f}f}f}f}f}f}f}\f}f}f}f}f}f}f}\f}f}f}f}f}f}f}f}\\f}f}\f}\\f}f}f}\\f}f}\f}fnfn\fnfn\fn\\\fn\fnfn\\fnfn}fn}fnfn\\\\\\\\\\fn 'Rightarrow {frac {fnK} {f} {fnMicroc} {fnK} {f} {f}} {fn}}} {fn}}} {fn}}} {fn} {fn}} {fn}}}}} {cdot}cdot} {f}} {f} {f} {f} {f} {f}}f}f}f}f}}f}c}}}}}}cdot}}}}cdot}c}c}c}c}c}c}}}c} {cdot} {c} {cdotcdot} {cdot}c}cdot} {cdotcdot} {c} {cdot} {cdotc}c}c}c}}c}}}}}}}}}}} Q}

R.=P+Q⋅ ⋅ PEd⋅ ⋅ Q=P()1+1Ed){displaystyle R'=P+Qcdot {frac {fnMicrosoft Sans Serif}

En un gráfico con una curva de demanda y una curva de ingreso marginal, la demanda será elástica en todas las cantidades donde el ingreso marginal sea positivo. La demanda es elástica unitaria en la cantidad donde el ingreso marginal es cero. La demanda es inelástica en todas las cantidades donde el ingreso marginal es negativo.

Efecto en todos los ingresos

Un conjunto de gráficos muestra la relación entre demanda e ingresos (PQ) para el caso específico de una curva de demanda lineal. A medida que el precio disminuye en el rango elástico, los ingresos aumentan, pero en el rango inelástico, los ingresos disminuyen. El ingreso es más alto en la cantidad donde la elasticidad es igual a 1.

Una empresa que esté considerando un cambio de precio debe saber qué efecto tendrá el cambio de precio en los ingresos totales. Los ingresos son simplemente el producto del precio unitario por la cantidad:

Ingresos=PQd{displaystyle {text{Revenue}=PQ_{d}

Por lo general, cualquier cambio en el precio tendrá dos efectos:

El efecto del precio

Para los bienes inelásticos, un aumento del precio unitario tenderá a aumentar los ingresos, mientras que una disminución del precio tenderá a disminuir los ingresos. (El efecto se revierte para las mercancías elásticas.)

El efecto de la cantidad

Un aumento del precio unitario tenderá a producir menos unidades vendidas, mientras que una disminución del precio unitario tenderá a producir más unidades vendidas.

Para los bienes inelásticos, debido a la naturaleza inversa de la relación entre el precio y la cantidad demandada (es decir, la ley de la demanda), los dos efectos afectan el ingreso total en direcciones opuestas. Pero al determinar si aumentar o disminuir los precios, una empresa necesita saber cuál será el efecto neto. La elasticidad proporciona la respuesta: el cambio porcentual en el ingreso total es aproximadamente igual al cambio porcentual en la cantidad demandada más el cambio porcentual en el precio. (Un cambio será positivo, el otro negativo). El cambio porcentual en la cantidad está relacionado con el cambio porcentual en el precio por elasticidad: por lo tanto, el cambio porcentual en los ingresos se puede calcular conociendo la elasticidad y el cambio porcentual en el precio solo.

Como resultado, la relación entre elasticidad e ingresos se puede describir para cualquier bien:

• Cuando la elasticidad de precio de la demanda para un bien es perfectamente inelástico ()E_d = 0), los cambios en el precio no afectan la cantidad demandada por el bien; subir los precios siempre causará un aumento de los ingresos totales. Los bienes necesarios para la supervivencia pueden clasificarse aquí; una persona racional estará dispuesta a pagar cualquier cosa por un bien si la alternativa es la muerte. Por ejemplo, una persona en el desierto débil y muriendo de sed daría fácilmente todo el dinero en su billetera, sin importar cuánto, por una botella de agua si de otro modo moriría. Su demanda no depende del precio.
• Cuando el precio elasticidad de la demanda es relativamente inelástico (1 - 1 E_d 0), el cambio porcentual de la cantidad demandada es menor que el precio. Por lo tanto, cuando el precio se eleva, el total de ingresos aumenta, y viceversa.
• Cuando el precio elasticidad de la demanda es unidad (o unitario) elástico ()E_d = −1), el cambio porcentual en la cantidad demandada es igual al precio, por lo que un cambio en el precio no afectará los ingresos totales.
• Cuando el precio elasticidad de la demanda es relativamente elástico (rígidos) E_d −1), el cambio porcentual de la cantidad demandada es mayor que el precio. Por lo tanto, cuando el precio se eleva, el ingreso total cae, y viceversa.
• Cuando el precio elasticidad de la demanda es perfectamente elástico ()E_d es − JUEGO), cualquier aumento del precio, no importa lo pequeño, causará la cantidad demandada por el bien para caer a cero. Por lo tanto, cuando el precio se eleva, el ingreso total cae a cero. Esta situación es típica de bienes que tienen su valor definido por la ley (como moneda fiat); si se vendiera un billete de cinco dólares por algo más de cinco dólares, nadie lo compraría [a menos que haya demanda de chistes económicos], así que la demanda es cero (asumiendo que el proyecto de ley no tiene una huella errónea o algo más que lo haría tener su propio valor inherente).

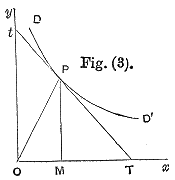
Por lo tanto, como muestra el diagrama adjunto, el ingreso total se maximiza en la combinación de precio y cantidad demandada donde la elasticidad de la demanda es unitaria.

Es importante darse cuenta de que la elasticidad precio de la demanda no es necesariamente constante en todos los rangos de precios. La curva de demanda lineal en el diagrama adjunto ilustra que los cambios en el precio también cambian la elasticidad: la elasticidad del precio es diferente en cada punto de la curva.

Efecto sobre la incidencia fiscal

Cuando la demanda es más inelástica que la oferta, los consumidores soportarán una mayor proporción de la carga tributaria que los productores.

La elasticidad de la demanda, en combinación con la elasticidad precio de la oferta, se puede utilizar para evaluar dónde está cayendo la incidencia (o "carga") de un impuesto por unidad o para predecir dónde caerá si el se impone el impuesto. Por ejemplo, cuando la demanda es perfectamente inelástica, por definición los consumidores no tienen otra alternativa que comprar el bien o servicio si el precio aumenta, por lo que la cantidad demandada se mantendría constante. Por lo tanto, los proveedores pueden aumentar el precio por el monto total del impuesto y el consumidor terminaría pagando la totalidad. En el caso contrario, cuando la demanda es perfectamente elástica, por definición los consumidores tienen una capacidad infinita para cambiar a alternativas si el precio aumenta, por lo que dejarían de comprar el bien o servicio en cuestión por completo: la cantidad demandada caer a cero. Como resultado, las empresas no pueden repercutir ninguna parte del impuesto aumentando los precios, por lo que se verían obligadas a pagarlo todo ellas mismas.

En la práctica, es probable que la demanda sea solo relativamente elástica o relativamente inelástica, es decir, en algún punto entre los casos extremos de elasticidad perfecta o inelasticidad. De manera más general, entonces, cuanto mayor sea la elasticidad de la demanda en comparación con PSA, mayor será la carga para los productores; por el contrario, cuanto más inelástica sea la demanda en comparación con la oferta, mayor será la carga para los consumidores. El principio general es que la parte (es decir, consumidores o productores) que tiene menos oportunidades de evitar el impuesto cambiando a alternativas soportará la mayor proporción de la carga fiscal. Al final, toda la carga fiscal la soportan los hogares individuales, ya que son los propietarios últimos de los medios de producción que utiliza la empresa (ver Flujo circular de ingresos).

PED y PES también pueden tener un efecto sobre la pérdida irrecuperable asociada con un régimen fiscal. Cuando PED, PES o ambos son inelásticos, la pérdida irrecuperable de eficiencia es menor que en un escenario comparable con mayor elasticidad.

Precio óptimo

Entre las aplicaciones más comunes de la elasticidad de precios se encuentra la determinación de precios que maximicen los ingresos o las ganancias.

Elasticidad constante y precios óptimos

Si se utiliza la elasticidad de un punto para modelar los cambios de la demanda en un rango finito de precios, se asume implícitamente que la elasticidad es constante con respecto al precio en el rango finito de precios. La ecuación que define la elasticidad precio de un producto se puede reescribir (omitiendo las variables secundarias) como una ecuación lineal.

LQ=K+E× × LP{displaystyle LQ=K+Etimes LP}

dónde

LQ=In⁡ ⁡ ()Q),LP=In⁡ ⁡ ()P),E{displaystyle LQ=ln(Q),LP=ln(P),E} es la elasticidad, y K{displaystyle K} es una constante.

Del mismo modo, las ecuaciones para la elasticidad cruzada n{displaystyle n} productos se pueden escribir como un conjunto de n{displaystyle n} ecuaciones lineales simultáneas.

LQl l =Kl l +El l ,k× × LPk{displaystyle LQ_{ell }=K_{ell }+E_{ellk}times LP^{k}

dónde

l l {displaystyle ell } y k=1,...... ,n,LQl l =In⁡ ⁡ ()Ql l ),LPl l =In⁡ ⁡ ()Pl l ){displaystyle k=1,dotscn,,,LQ_{ell }=ln(Q_{ell }),LP^{ell }=ln(P^{ell })}, y Kl l {displaystyle K_{ell } son constantes; y la aparición de un índice de letras como un índice superior y un índice inferior en el mismo término implica la suma sobre ese índice.

Esta forma de las ecuaciones muestra que las elasticidades de puntos asumen constante sobre un rango de precios no pueden determinar qué precios generan valores máximos In⁡ ⁡ ()Q){displaystyle ln(Q)}; similarmente no pueden predecir precios que generan el máximo Q{displaystyle Q} o ingresos máximos.

Las elasticidades constantes pueden predecir el precio óptimo solo calculando elasticidades puntuales en varios puntos, para determinar el precio en el que la elasticidad puntual es igual a −1 (o, para productos múltiples, el conjunto de precios en el que la matriz de elasticidad puntual es la identidad negativa matriz).

Elasticidad no constante y precios óptimos

Si la definición de elasticidad de precio se extiende para producir una relación cuadrática entre unidades de demanda (Q{displaystyle Q}) y precio, entonces es posible calcular precios que maximicen In⁡ ⁡ ()Q){displaystyle ln(Q)}, Q{displaystyle Q}e ingresos. La ecuación fundamental para un producto se convierte en

LQ=K+E1× × LP+E2× × LP2{displaystyle LQ=K+E_{1}times LP+E_{2}times LP^{2}

y la ecuación correspondiente para varios productos se convierte en

LQl l =Kl l +E1l l ,k× × LPk+E2l l ,k× × ()LPk)2{displaystyle LQ_{ell }=K_{ell }+E1_{ellk}times ¿Qué?

Hay modelos de Excel disponibles que calculan la elasticidad constante y utilizan la elasticidad no constante para estimar los precios que optimizan los ingresos o las ganancias de uno o varios productos.

Limitaciones de las estrategias de maximización de ingresos

En la mayoría de las situaciones, como aquellas con costos variables distintos de cero, los precios que maximizan los ingresos no son precios que maximizan las ganancias. Para estas situaciones, es más apropiado utilizar una técnica de maximización de beneficios.

Elasticidades de precio seleccionadas

Se utilizan varios métodos de investigación para calcular las elasticidades de los precios en la vida real, incluido el análisis de datos históricos de ventas, tanto públicos como privados, y el uso de encuestas actuales de clientes' preferencias para construir mercados de prueba capaces de modelar tales cambios. Alternativamente, se puede utilizar el análisis conjunto (una clasificación de las preferencias de los usuarios que luego se pueden analizar estadísticamente). Las estimaciones aproximadas de la elasticidad precio se pueden calcular a partir de la elasticidad ingreso de la demanda, en condiciones de independencia de las preferencias. Este enfoque se ha validado empíricamente utilizando paquetes de bienes (por ejemplo, alimentos, atención médica, educación, recreación, etc.).

Aunque las elasticidades para la mayoría de los programas de demanda varían según el precio, se pueden modelar suponiendo una elasticidad constante. Usando este método, las elasticidades para varios bienes, que pretenden actuar como ejemplos de la teoría descrita anteriormente, son las siguientes. Para obtener sugerencias sobre por qué estos bienes y servicios pueden tener la elasticidad que se muestra, consulte la sección anterior sobre los determinantes de la elasticidad de los precios.