La curva de Viviani.

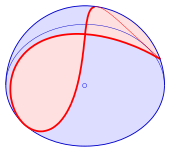
En matemáticas, la curva de Viviani, también conocida como ventana de Viviani, es una curva espacial en forma de ocho que lleva el nombre del matemático italiano Vincenzo. Viviani. Es la intersección de una esfera con un cilindro que es tangente a la esfera y pasa por dos polos (un diámetro) de la esfera (ver diagrama). Antes de Viviani, esta curva fue estudiada por Simon de La Loubère y Gilles de Roberval.

La proyección ortográfica de la curva de Viviani sobre un plano perpendicular a la recta que pasa por el punto de cruce y el centro de la esfera es la lemniscata de Gerono, mientras que la proyección estereográfica es una hipérbola o la lemniscata de Bernoulli, dependiendo de cuál El punto en la misma línea se utiliza para proyectar.

En 1692 Viviani resolvió la siguiente tarea: Corte de una media esfera (radius) r{displaystyle r}) dos ventanas, de tal manera que la superficie restante (de la media esfera) puede ser cuadrada, es decir, una plaza con la misma zona se puede construir utilizando sólo brújulas y gobernante. Su solución tiene un área de 4r2{displaystyle 4r^{2} (véase infra).

Ecuaciones

Para mantener simple la prueba de elevar al cuadrado,

el esfera tiene la ecuación x2+Sí.2+z2=r2{displaystyle ;x^{2}+y^{2}+z^{2}=r^{2};}

y

el el cilindro está derecho con ecuación x2+Sí.2− − rx=0{displaystyle ;x^{2}+y^{2}-rx=0;}.

El cilindro tiene radio r/2{displaystyle r/2} y es tangente a la esfera en punto ()r,0,0) .{displaystyle (r,0,0)}

Propiedades de la curva

Planta, alzado y planta lateral

Eliminación de la x{displaystyle x} Sí.{displaystyle y} z{displaystyle z} rendimientos respectivamente:

La proyección ortogonal de la curva de intersección sobre la

x{displaystyle x}-Sí.{displaystyle y}- El avión es el círculo con ecuación ()x− − r2)2+Sí.2=()r2)2 .{displaystyle ;left(x-{tfrac {fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc}}}}derecho)}

x{displaystyle x}-z{displaystyle z}-plane el parabola con ecuación x=− − 1rz2+r.{displaystyle ;x=-{tfrac {1}{2}+r;}

Sí.{displaystyle y}-z{displaystyle z}-plane la curva algebraica con la ecuación z4+r2()Sí.2− − z2)=0.{displaystyle ;z^{4}+r^{2}(y^{2}-z^{2})=0;}

Representación paramétrica

Representando la esfera por

x=r⋅ ⋅ #⁡ ⁡ Silencio Silencio ⋅ ⋅ #⁡ ⁡ φ φ Sí.=r⋅ ⋅ #⁡ ⁡ Silencio Silencio ⋅ ⋅ pecado⁡ ⁡ φ φ z=r⋅ ⋅ pecado⁡ ⁡ Silencio Silencio − − π π 2≤ ≤ Silencio Silencio ≤ ≤ π π 2 , − − π π ≤ ≤ φ φ ≤ ≤ π π ,{cdotcdotcdotcdotcdotcdotcdotcdotcdot cos varphi \y implica= limitrcdot cos theta cdot sin varphiz= limitrcdot sintheta qquadqquad {tfracc] }{2}\ -pi leq varphi leq pi ;,end{array}}

y configuración φ φ =Silencio Silencio ,{displaystyle ;varphi =theta;} cede la curva

x=r⋅ ⋅ #⁡ ⁡ Silencio Silencio ⋅ ⋅ #⁡ ⁡ Silencio Silencio Sí.=r⋅ ⋅ #⁡ ⁡ Silencio Silencio ⋅ ⋅ pecado⁡ ⁡ Silencio Silencio z=r⋅ ⋅ pecado⁡ ⁡ Silencio Silencio − − π π 2≤ ≤ Silencio Silencio ≤ ≤ π π 2 .{cdotcdotcdotcdotcdotcdotcdotcdot cos theta \cdotcdotcdot cos theta cdot sin thetacdotcdot qdot sintheta qquadqquad {tfracc]

Se comprueba fácilmente que la curva esférica cumple la ecuación del cilindro. Pero los límites permiten solamente la parte roja (ver diagrama) de la curva de Viviani. La segunda mitad desaparecida (verde) tiene la propiedad φ φ =− − Silencio Silencio .{displaystyle ;color {verde}varphi =-theta ;.}

Con la ayuda de esta representación paramétrica es fácil probar la declaración: El área de la media esfera (contiene la curva de Viviani) menos el área de las dos ventanas es 4r2{displaystyle 4r^{2}. El área de la parte superior derecha de la ventana de Viviani (ver diagrama) se puede calcular mediante una integración:

∫ ∫ Sspherer2#⁡ ⁡ Silencio Silencio dSilencio Silencio dφ φ =r2∫ ∫ 0π π /2∫ ∫ 0Silencio Silencio #⁡ ⁡ Silencio Silencio dφ φ dSilencio Silencio =r2()π π 2− − 1) .{displaystyle iint ¿Qué? theta ,mathrm {d} theta ,mathrm {d} varphi =r^{2}int ################################################################################################################################################################################################################################################################ {0} {theta }cos theta ,mathrm {d} varphi ,mathrm {d} theta =r^{2}left({frac {pi - Sí.

Por lo tanto el área total de la superficie esférica incluida por la curva de Viviani es 2π π r2− − 4r2{displaystyle 2pi r^{2}-4r^{2} y el área de la media esfera (2π π r2{displaystyle 2pi r^{2}) menos la zona de la ventana de Viviani es 4r2{displaystyle ;4r^{2};}, el área de un cuadrado con el diámetro de la esfera como la longitud de un borde.

Representación racional de Bézier

El cuarto de la curva de Viviani que se encuentra en el cuadrante totalmente positivo del espacio 3D no puede representarse exactamente mediante una curva de Bézier regular de ningún grado.

Sin embargo, se puede representar exactamente mediante un segmento de Bézier racional 3D de grado 4, y existe una familia infinita de puntos de control de Bézier racionales que generan ese segmento.

Una posible solución viene dada por los siguientes cinco puntos de control:

p0=[0011]p1=[01221212]p2=[13121223]p3=[1212212212]p4=[1001]{displaystyle {boldsymbol {}={begin{bmatrix}011end{bmatrix}{boldsymbol {p1}={begin{bmatrix}0\{frac {1}{2{sqrt {2}}\{frac {1}{sqrt {2}}\\frac {1}{sqrt {2}}}}end{bmatrix}}}} {\boldsymbol}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {p2}={begin{bmatrix}{frac {1}{3}\\\\fnK}\\fnK}\\\\\fn}\\\\\fn}\\\\\\fn}\\\\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\\fn {1}{2}\\\\fnK}}end{bmatrix}{boldsymbol {p3}={begin{bmatrix}{frac {1} {sqrt {2}\fn} {2}}\\fn}\\sqrt {2} {2}}}\\\\\\sqrt {2}}} {f} {f}} {f}} {fn}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {p4}={begin{bmatrix}11end{bmatrix}}}

La parametrización racional correspondiente es:

()2μ μ 2()μ μ 2− − 2()2+2)μ μ +42+6)()2()μ μ − − 1)μ μ +2+2)22()μ μ − − 1)μ μ ()()μ μ − − 1)μ μ − − 32− − 4)()2()μ μ − − 1)μ μ +2+2)2− − ()μ μ − − 1)()2μ μ +2+2)2()μ μ − − 1)μ μ +2+2)μ μ ▪ ▪ [0,1]{displaystyle left({begin{c}{c}{frac {2mu ^{2}left(mu ^{2}-2left(2+{sqrt {2}right)mu +4{sqrt {2}+6right)}{left(2(mu -1)mu {2sqrt {2}+2right)}\{2}{frac {2(mu -1)muleft(mu -1)mu -3{sqrt {2}-4right)}{left(2(mu -1)mu -1)mu {fnMicroc {fnMicrosoft Sans Serif}m}m}m}m}m}m} {2}+2}}{2(mu -1)mu ### {sqrt {2}+2}\end{array}right];muin left[0,1right]}

Relación con otras curvas

• La elevación en forma de 8 (ver arriba) es un Lemniscate de Gerono.
• La curva de Viviani es una curva Clelia especial. Para una curva Clelia la relación entre los ángulos es φ φ =cSilencio Silencio .{displaystyle ;varphi =c;theta ;.}

Restar 2× la ecuación del cilindro de la ecuación de la esfera y aplicar completar el cuadrado lleva a la ecuación

()x− − r)2+Sí.2=z2,{displaystyle (x-r)^{2}+y^{2}=z^{2};

que describe un cono circular derecho con su ápice ()r,0,0){displaystyle ;(r,0,0);}El doble punto de la curva de Viviani. Por lo tanto

• La curva de Viviani se puede considerar no sólo como la curva de intersección de una esfera y un cilindro, sino también como

a) la intersección de una esfera y un cono y como

b) la intersección de un cilindro y un cono.