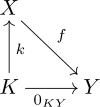Kernel (teoría de categorías)

En la teoría de categorías y sus aplicaciones a otras ramas de las matemáticas, los núcleos son una generalización de los núcleos de los homomorfismos de grupos, los núcleos de los homomorfismos de módulos y algunos otros núcleos del álgebra. Intuitivamente, el núcleo del morfismo f: X → Y es el "más general" morfismo k: K → X que da cero cuando se compone con (seguido de) f.

Tenga en cuenta que los pares de núcleos y los núcleos de diferencia (también conocidos como ecualizadores binarios) a veces reciben el nombre de "núcleo"; si bien están relacionados, no son exactamente lo mismo y no se tratan en este artículo.

Definición

Sea C una categoría. Para definir un kernel en el sentido general de la teoría de categorías, C necesita tener cero morfismos. En ese caso, si f: X → Y es un morfismo arbitrario en C, entonces un núcleo de f es un ecualizador de f y el morfismo cero de X a Y. En símbolos:

ker(f) = eq(f, 0_XY)

Para ser más explícito, se puede usar la siguiente propiedad universal. Un núcleo de f es un objeto K junto con un morfismo k: K → X tal que:

• f∘k es el morfismo cero de K a Y;

• Dada cualquier morfismo k′: K′ → X tales que f∘k′ es el morfismo cero, hay un morfismo único u: K′ → K tales que k∘u = k.

Tenga en cuenta que en muchos contextos concretos, uno se referiría al objeto K como el "núcleo", en lugar del morfismo k. En esas situaciones, K sería un subconjunto de X, y eso sería suficiente para reconstruir k como un mapa de inclusión; en el caso no concreto, por el contrario, necesitamos el morfismo k para describir cómo K debe interpretarse como un subobjeto de X . En cualquier caso, se puede demostrar que k es siempre un monomorfismo (en el sentido categórico). Uno puede preferir pensar en el kernel como el par (K, k) en lugar de simplemente K o k solo.

No todos los morfismos necesitan tener un kernel, pero si lo tienen, entonces todos sus kernels son isomorfos en un sentido fuerte: if k: K → X y ℓ: L → X son núcleos de f: X → Y, entonces existe un único isomorfismo φ: K → L tal que ℓ∘φ = k.

Ejemplos

Los núcleos son familiares en muchas categorías del álgebra abstracta, como la categoría de grupos o la categoría de módulos (izquierda) sobre un anillo fijo (incluidos los espacios vectoriales sobre un campo fijo). Para ser explícito, si f: X → Y es un homomorfismo en una de estas categorías, y K es su núcleo en el sentido algebraico habitual, entonces K es una subálgebra de X y el homomorfismo de inclusión de K a X es un kernel en el sentido categórico.

Tenga en cuenta que en la categoría de monoides, existen núcleos teóricos de categorías al igual que para los grupos, pero estos núcleos no contienen suficiente información para fines algebraicos. Por lo tanto, la noción de kernel estudiada en la teoría monoide es ligeramente diferente (ver #Relación con los kernels algebraicos a continuación).

En la categoría de anillos unitarios, no hay núcleos en el sentido teórico de la categoría; de hecho, esta categoría ni siquiera tiene morfismos cero. Sin embargo, todavía existe una noción de kernel estudiada en la teoría de anillos que corresponde a kernels en la categoría de anillos no unitarios.

En la categoría de espacios topológicos puntiagudos, si f: X → Y es un mapa puntiagudo continuo, entonces la preimagen del distinguido el punto, K, es un subespacio de X. El mapa de inclusión de K en X es el núcleo categórico de f.

Relación con otros conceptos categóricos

El concepto dual al de kernel es el de cokernel. Es decir, el núcleo de un morfismo es su conúcleo en la categoría opuesta, y viceversa.

Como se mencionó anteriormente, un kernel es un tipo de ecualizador binario o kernel de diferencia. Por el contrario, en una categoría preaditiva, cada ecualizador binario se puede construir como un núcleo. Para ser específicos, el ecualizador de los morfismos f y g es el núcleo de la diferencia g − f. En símbolos:

eq (f,g♪ = ker ()g − f).

Es por este hecho que los ecualizadores binarios se denominan "núcleos de diferencia", incluso en categorías no aditivas donde los morfismos no se pueden restar.

Cada kernel, como cualquier otro ecualizador, es un monomorfismo. Por el contrario, un monomorfismo se llama normal si es el núcleo de algún morfismo. Una categoría se llama normal si todos los monomorfismos son normales.

Las categorías abelianas, en particular, son siempre normales. En esta situación, el núcleo del conúcleo de cualquier morfismo (que siempre existe en una categoría abeliana) resulta ser la imagen de ese morfismo; en símbolos:

im f = ker coker f (en una categoría abeliana)

Cuando m es un monomorfismo, debe ser su propia imagen; por lo tanto, no solo las categorías abelianas son normales, de modo que todo monomorfismo es un núcleo, sino que también sabemos de qué morfismo el monomorfismo es un núcleo, a saber, su conúcleo. En símbolos:

m = ker (coker) m) (para monomorfismos en una categoría abeliana)

Relación con núcleos algebraicos

El álgebra universal define una noción de núcleo para homomorfismos entre dos estructuras algebraicas del mismo tipo. Este concepto de núcleo mide qué tan lejos está el homomorfismo dado de ser inyectivo. Existe cierta superposición entre esta noción algebraica y la noción categórica de núcleo, ya que ambas generalizan la situación de grupos y módulos mencionada anteriormente. En general, sin embargo, la noción algebraica universal de núcleo se parece más al concepto de teoría de categorías de par de núcleos. En particular, los pares de núcleos se pueden usar para interpretar los núcleos en la teoría monoide o la teoría de anillos en términos de teoría de categorías.