Junta universal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Mecanismo con eje de rotación doblable

Una articulación universal

Una junta universal (también llamada acoplamiento universal o junta en U) es una junta o acoplamiento que conecta ejes rígidos cuyos ejes están inclinados el uno al otro Se usa comúnmente en ejes que transmiten movimiento rotatorio. Consiste en un par de bisagras ubicadas juntas, orientadas a 90° entre sí, conectadas por un eje transversal. La junta universal no es una junta de velocidad constante.

Las juntas universales también reciben a veces varios nombres epónimos, como se indica a continuación:

Conjunto de cartón, después de Gerolamo Cardano, un polímero del siglo XVI que contribuyó al conocimiento de diversos mecanismos inteligentes, incluyendo gimbals
Junta de Hooke o Junta de Hooke, después de Robert Hooke, un polimatismo del siglo XVII que contribuyó al conocimiento de diversos mecanismos inteligentes
Junta de especias, después de Clarence W. Spicer y la Spicer Manufacturing Company, que fabricó U joints
Hardy Spicer joint, después de la marca Hardy Spicer, un sucesor de la marca Spicer

Historia

Este vídeo muestra diferentes partes y funcionamiento del eje universal.

Juntas universales para automotores, 1916.

El concepto principal de la junta universal se basa en el diseño de cardanes, que se han utilizado desde la antigüedad. Una anticipación de la junta universal fue su uso por parte de los antiguos griegos en balistas. En Europa, la junta universal a menudo se llama junta Cardano (y un eje de transmisión que usa las juntas, un eje cardánico), en honor al matemático italiano Gerolamo Cardano, quien fue uno de los primeros escritores sobre cardanes, aunque sus escritos mencionan solo montajes de cardanes, no juntas universales.

El mecanismo fue descrito más tarde en Technica curiosa sive mirabilia artis (1664) por Gaspar Schott, quien afirmó erróneamente que se trataba de una articulación de velocidad constante. Poco después, entre 1667 y 1675, Robert Hooke analizó la junta y descubrió que su velocidad de rotación no era uniforme, pero que esta propiedad podía usarse para seguir el movimiento de la sombra en la esfera de un reloj de sol. De hecho, el componente de la ecuación del tiempo que explica la inclinación del plano ecuatorial con respecto a la eclíptica es completamente análogo a la descripción matemática de la junta universal. El primer uso registrado del término articulación universal para este dispositivo fue por Hooke en 1676, en su libro Helioscopios. Publicó una descripción en 1678, lo que resultó en el uso del término articulación de Hooke en el mundo de habla inglesa. En 1683, Hooke propuso una solución a la velocidad de rotación no uniforme de la junta universal: un par de juntas de Hooke desfasadas 90° en cada extremo de un eje intermedio, una disposición que ahora se conoce como un tipo de junta universal. -junta de velocidad. Christopher Polhem de Suecia más tarde reinventó la junta universal, dando origen al nombre Polhemsknut ("nudo de Polhem") en sueco.

En 1841, el científico inglés Robert Willis analizó el movimiento de la junta universal. En 1845, el ingeniero y matemático francés Jean-Victor Poncelet había analizado el movimiento de la junta universal mediante trigonometría esférica.

El término junta universal se utilizó en el siglo XVIII y era de uso común en el siglo XIX. La patente de Edmund Morewood de 1844 para una máquina de recubrimiento de metal requería una junta universal, con ese nombre, para acomodar pequeños errores de alineación entre el motor y los ejes del tren de laminación. La patente de locomotora de Ephriam Shay de 1881, por ejemplo, usó juntas universales dobles en el eje de transmisión de la locomotora. Charles Amidon usó una junta universal mucho más pequeña en su bit-brace patentado en 1884. La máquina de vapor esférica, rotativa y de alta velocidad de Beauchamp Tower usó una adaptación de la junta universal alrededor de 1885.

El término articulación cardán parece haber llegado tarde al idioma inglés. Muchos de los primeros usos del siglo XIX aparecen en traducciones del francés o están fuertemente influenciados por el uso francés. Los ejemplos incluyen un informe de 1868 sobre la Exposición Universal de 1867 y un artículo sobre el dinamómetro traducido del francés en 1881.

En el siglo XX, Clarence W. Spicer y Spicer Manufacturing Company, así como la marca sucesora de Hardy Spicer, ayudaron a popularizar aún más las juntas universales en las industrias automotriz, de equipos agrícolas, equipos pesados y maquinaria industrial.

Ecuación de movimiento

Diagrama de variables para la articulación universal. El eje 1 es perpendicular al plano rojo y el eje 2 es perpendicular al plano azul en todo momento. Estos aviones están en un ángulo β con respecto al otro. El desplazamiento angular (Posición rotacional) de cada eje es dado por

gamma _{1}

gamma _{2}

respectivamente, que son los ángulos de los vectores de unidad

{hat {x}}_{1}

{hat {x}}_{2}

con respecto a sus posiciones iniciales a lo largo del eje x y y. El

{hat {x}}_{1}

{hat {x}}_{2}

Los vectores son fijos por el gimbal que conecta los dos ejes y por lo tanto se limitan a permanecer perpendicular entre sí en todo momento.

Una muestra universal de conjunto codificado a los diagramas sobre la ecuación del movimiento. Los planos rojo y azul son visibles.

Velocidad de salida angular (rotacional)

omega _{2},

versus ángulo de rotación

gamma _{1},

para diferentes ángulos de curvatura

beta ,

de la Junta

Ángulo de rotación del eje de salida,

gamma _{2},

contra ángulo de rotación del eje de entrada

gamma _{1},

para diferentes ángulos de curvatura

beta ,

de la Junta

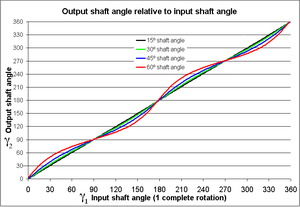
La junta cardánica tiene un problema importante: incluso cuando el eje del eje de transmisión de entrada gira a una velocidad constante, el eje del eje de transmisión de salida gira a una velocidad variable, lo que provoca vibraciones y desgaste. La variación de la velocidad del eje conducido depende de la configuración de la junta, la cual viene especificada por tres variables:

$gamma _{1}$ el ángulo de rotación para el eje 1
$gamma _{2}$ el ángulo de rotación para eje 2
$beta$ el ángulo de curvatura de la articulación, o ángulo de los ejes con respecto a uno al otro, con cero siendo paralelo o recto a través.

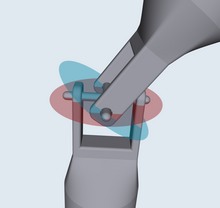
Estas variables se ilustran en el diagrama de la derecha. También se muestra un conjunto de ejes de coordenadas fijos con vectores de unidad ${hat {mathbf {x} }}$ y ${hat {mathbf {y} }}$ y los planos de rotación de cada eje. Estos planos de rotación son perpendiculares a los ejes de rotación y no se mueven a medida que los ejes giran. Los dos ejes están unidos por un gimbal que no se muestra. Sin embargo, el eje 1 se adhiere al gimbal en los puntos rojos en el plano rojo de rotación en el diagrama, y el eje 2 se adjunta en los puntos azules en el plano azul. Los sistemas de coordenadas fijos con respecto a los ejes giratorios se definen como tener sus vectores de unidad de eje x ( ${hat {mathbf {x} }}_{1}$ y ${hat {mathbf {x} }}_{2}$ ) señalando desde el origen hacia uno de los puntos de conexión. Como se muestra en el diagrama, ${hat {mathbf {x} }}_{1}$ está en ángulo $gamma _{1}$ con respecto a su posición inicial a lo largo de la x axis y ${hat {mathbf {x} }}_{2}$ está en ángulo $gamma _{2}$ con respecto a su posición inicial a lo largo de la Sí. Axis.

${hat {mathbf {x} }}_{1}$ se limita al "plano rojo" en el diagrama y se relaciona con $gamma _{1}$ por:

{displaystyle {hat {mathbf {x} }}_{1}=left[cos gamma _{1},,,sin gamma _{1},,,0right]}

${hat {mathbf {x} }}_{2}$ se limita al "plano azul" en el diagrama y es el resultado del vector de unidad en el x axis ${displaystyle {hat {x}}=[1,0,0]}$ girando a través de ángulos Euler ${displaystyle [pi !/2,,,beta ,,,gamma _{2}}$ ]:

{displaystyle {hat {mathbf {x} }}_{2}=left[-cos beta sin gamma _{2},,,cos gamma _{2},,,sin beta sin gamma _{2}right]}

Un obstáculo para ${hat {mathbf {x} }}_{1}$ y ${hat {mathbf {x} }}_{2}$ vectores es que ya que están fijos en el gimbal, deben permanecer en ángulos rectos entre sí. Esto es así cuando su producto de punto equivale a cero:

{displaystyle {hat {mathbf {x} }}_{1}cdot {hat {mathbf {x} }}_{2}=0}

Por lo tanto, la ecuación de movimiento que relaciona las dos posiciones angulares está dada por:

{displaystyle tan gamma _{1}=cos beta tan gamma _{2},}

con una solución formal $gamma _{2}$ :

{displaystyle gamma _{2}=tan ^{-1}left[tan gamma _{1}sec beta right],}

La solución para $gamma _{2}$ no es único ya que la función arctangent es multivalorada, sin embargo se requiere que la solución para $gamma _{2}$ ser continuo sobre los ángulos de interés. Por ejemplo, la siguiente solución explícita usando la función atan2(y, x) será válida para $<math alttext="{displaystyle -pi <gamma _{1}− − π π .γ γ 1.π π {displaystyle -pi }Seguido<img alt="-pi <gamma _{1}$ :

{displaystyle gamma _{2}=operatorname {atan2} left(sin gamma _{1},cos beta ,cos gamma _{1}right)}

Los ángulos $gamma _{1}$ y $gamma _{2}$ en una articulación giratoria serán funciones de tiempo. Diferir la ecuación del movimiento con respecto al tiempo y utilizar la ecuación del movimiento mismo para eliminar una variable produce la relación entre las velocidades angulares ${displaystyle omega _{1}=dgamma _{1}/dt}$ y ${displaystyle omega _{2}=dgamma _{2}/dt}$ :

{displaystyle omega _{2}=omega _{1}left({frac {cos beta }{1-sin ^{2}beta ,cos ^{2}gamma _{1}}}right)}

Como se muestra en las parcelas, las velocidades angulares no están relacionadas linealmente, sino que son periódicas con un período de la mitad de los ejes giratorios. La ecuación de velocidad angular se puede diferenciar de nuevo para conseguir la relación entre las aceleraciones angulares $a_{1}$ y $a_{2}$ :

{displaystyle a_{2}={frac {a_{1}cos beta }{1-sin ^{2}beta ,cos ^{2}gamma _{1}}}-{frac {omega _{1}^{2}cos beta ,sin ^{2}beta ,sin 2gamma _{1}}{left(1-sin ^{2}beta ,cos ^{2}gamma _{1}right)^{2}}}}

Doble eje cardán

Juntas universales en un driveshaft

Una configuración conocida como eje de transmisión de junta cardán doble soluciona parcialmente el problema de la rotación brusca. Esta configuración utiliza dos juntas en U unidas por un eje intermedio, con la segunda junta en U en fase en relación con la primera junta en U para cancelar la velocidad angular cambiante. En esta configuración, la velocidad angular del eje impulsado coincidirá con la del eje impulsor, siempre que tanto el eje impulsor como el eje impulsado estén en ángulos iguales con respecto al eje intermedio (pero no necesariamente en el mismo plano) y que las dos juntas universales están desfasadas 90 grados. Este conjunto se emplea comúnmente en vehículos de tracción trasera, donde se conoce como eje de transmisión o eje de propulsión.

Incluso cuando los ejes impulsor e impulsado forman ángulos iguales con respecto al eje intermedio, si estos ángulos son mayores que cero, se aplican momentos oscilantes a los tres ejes a medida que giran. Estos tienden a doblarlos en una dirección perpendicular al plano común de los ejes. Esto aplica fuerzas a los cojinetes de soporte y puede causar "sacudidas de lanzamiento" en vehículos de tracción trasera. El eje intermedio también tendrá una componente sinusoidal en su velocidad angular, lo que contribuye a la vibración y las tensiones.

Matemáticamente, esto se puede mostrar como sigue: Si $gamma _{1},$ y $gamma _{2},$ son los ángulos para la entrada y salida de la articulación universal que conecta la unidad y los ejes intermedios respectivamente, y $gamma _{3},$ y $gamma _{4},$ son los ángulos para la entrada y salida de la articulación universal que conecta los ejes intermedios y de salida respectivamente, y cada par está en ángulo $beta ,$ con respecto al otro, entonces:

{displaystyle tan gamma _{2}=cos beta ,tan gamma _{1}qquad tan gamma _{4}=cos beta ,tan gamma _{3}}

Si la segunda articulación universal se gira 90 grados con respecto a la primera, entonces ${displaystyle gamma _{3}=gamma _{2}+pi /2}$ . Usando el hecho de que ${displaystyle tan(gamma +pi /2)=1/tan gamma }$ rendimientos:

{displaystyle tan gamma _{4}={frac {cos beta }{tan gamma _{2}}}={frac {1}{tan gamma _{1}}}=tan left(gamma _{1}+{frac {pi }{2}}right),}

y se ve que la transmisión de salida está desfasada solo 90 grados con respecto al eje de entrada, lo que produce una transmisión de velocidad constante.

NOTA: La referencia para medir los ángulos de los ejes de entrada y salida de la junta universal son ejes mutuamente perpendiculares. Entonces, en sentido absoluto, las horquillas del eje intermedio son paralelas entre sí. (Dado que una horquilla actúa como entrada y la otra horquilla actúa como salida para los ejes y se menciona una diferencia de fase superior a 90 grados entre las horquillas).

Doble junta cardán

Una junta cardán doble consta de dos juntas universales montadas espalda con espalda con un yugo central; el yugo central reemplaza el eje intermedio. Siempre que el ángulo entre el eje de entrada y el yugo central sea igual al ángulo entre el yugo central y el eje de salida, la segunda articulación cardánica cancelará los errores de velocidad introducidos por la primera articulación cardánica y la doble articulación cardánica alineada actuará como un Junta homocinética.

Acoplamiento Thompson

Un acoplamiento Thompson es una versión refinada de la junta cardán doble. Ofrece una eficiencia ligeramente mayor con la penalización de un gran aumento en la complejidad.

Contenido relacionado

Más resultados...