Juan Wallis

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Matemático inglés (1616-1703)

John Wallis (latín: Wallisius; 3 de diciembre [OS 23 de noviembre] 1616 – 8 de noviembre [OS 28 de octubre] 1703) fue un inglés clérigo y matemático a quien se le da crédito parcial por el desarrollo del cálculo infinitesimal. Entre 1643 y 1689 se desempeñó como criptógrafo jefe del Parlamento y, más tarde, de la corte real. Se le atribuye la introducción del símbolo ∞ para representar el concepto de infinito. De manera similar, usó 1/∞ para un infinitesimal. John Wallis fue contemporáneo de Newton y uno de los más grandes intelectuales del primer renacimiento de las matemáticas.

Biografía

Antecedentes educativos

Cambridge, M.A., Oxford, D.D.
Escuela de Gramática en Tenterden, Kent, 1625-31.
Escuela de Martin Holbeach en Felsted, Essex, 1631–2.
Cambridge University, Emmanuel College, 1632–40; B.A., 1637; M.A., 1640.
D.D. en Oxford en 1654

Familia

El 14 de marzo de 1645{{|date=septiembre de 2019}} se casó con Susanna Glynde (c. 1600 – 16 de marzo de 1687).{{|date=septiembre de 2019}} Tuvieron tres hijos:

Anne Blencoe (4 de junio de 1656 – 5 de abril de 1718),{{ vidasdate=septiembre de 2019}} se casó con Sir John Blencowe (30 de noviembre de 1642 – 6 de mayo de 1726){← permaneceda=septiembre de 2019} en 1675, con emisión
John Wallis (26 de diciembre de 1650 a 14 de marzo de 1717),{{ vidasdate=septiembre de 2019} MP para Wallingford 1690-1695, se casó con Elizabeth Harris (d. 1693) el 1 de febrero de 1682,{←date=septiembre de 2019} con el tema: un hijo y dos hijas
Elizabeth Wallis (1658-1703), casado William Benson (1649-1691) de Towcester, murió sin ningún problema

Vida

John Wallis nació en Ashford, Kent. Fue el tercero de cinco hijos del reverendo John Wallis y Joanna Chapman. Inicialmente fue educado en una escuela en Ashford, pero se mudó a la escuela de James Movat en Tenterden en 1625 luego de un brote de peste. Wallis estuvo expuesto por primera vez a las matemáticas en 1631, en Felsted School (entonces conocida como la escuela de Martin Holbeach en Felsted); disfrutaba de las matemáticas, pero su estudio era errático, ya que "las matemáticas, en ese momento entre nosotros, eran vistas poco como estudios académicos, sino mecánicos" (Scriba 1970). En la escuela de Felsted, Wallis aprendió a hablar y escribir en latín. En ese momento, también dominaba el francés, el griego y el hebreo. Como estaba previsto que fuera médico, fue enviado en 1632 al Emmanuel College de Cambridge. Mientras estuvo allí, mantuvo un acto sobre la doctrina de la circulación de la sangre; se dijo que esa había sido la primera ocasión en Europa en la que esta teoría se mantuvo públicamente en una disputa. Sus intereses, sin embargo, se centraron en las matemáticas. Recibió su título de Licenciado en Artes en 1637 y una Maestría en 1640, ingresando luego al sacerdocio. De 1643 a 1649, se desempeñó como escriba sin derecho a voto en la Asamblea de Westminster. Fue elegido para una beca en Queens' College, Cambridge en 1644, de la que tuvo que dimitir tras su matrimonio.

A lo largo de este tiempo, Wallis había estado cerca del partido parlamentario, quizás como resultado de su exposición a Holbeach en Felsted School. Les prestó una gran ayuda práctica para descifrar los despachos realistas. La calidad de la criptografía en ese momento fue mixta; a pesar de los éxitos individuales de matemáticos como François Viète, los principios subyacentes al diseño y análisis de cifrado se entendieron muy poco. La mayoría de los cifrados eran métodos ad hoc que se basaban en un algoritmo secreto, a diferencia de los sistemas basados en una clave variable. Wallis se dio cuenta de que estos últimos eran mucho más seguros, e incluso los describió como "irrompibles", aunque no confiaba lo suficiente en esta afirmación como para animar a revelar algoritmos criptográficos. También estaba preocupado por el uso de cifras por parte de potencias extranjeras, rechazando, por ejemplo, la solicitud de Gottfried Leibniz de 1697 de enseñar criptografía a los estudiantes de Hannover.

Al regresar a Londres (había sido nombrado capellán de St Gabriel Fenchurch en 1643), Wallis se unió al grupo de científicos que más tarde se convertiría en la Royal Society. Finalmente pudo satisfacer sus intereses matemáticos, dominando la Clavis Mathematicae de William Oughtred en unas pocas semanas en 1647. Pronto comenzó a escribir sus propios tratados, que trataban una amplia gama de temas, que continuó por el resto de su vida. Wallis escribió la primera encuesta sobre conceptos matemáticos en Inglaterra, donde discutió el sistema hindú-árabe.

Wallis se unió a los presbiterianos moderados al firmar la protesta contra la ejecución de Carlos I, por lo que incurrió en la hostilidad duradera de los independientes. A pesar de su oposición, fue nombrado en 1649 para la Cátedra Savilian de Geometría en la Universidad de Oxford, donde vivió hasta su muerte el 8 de noviembre [O.S. 28 de octubre] 1703. En 1650, Wallis fue ordenado ministro. Después, pasó dos años con Sir Richard Darley y Lady Vere como capellán privado. En 1661, fue uno de los doce representantes presbiterianos en la Conferencia de Saboya.

Además de sus obras matemáticas, escribió sobre teología, lógica, gramática inglesa y filosofía, y participó en el diseño de un sistema para enseñar a hablar a un niño sordo en Littlecote House. William Holder había enseñado anteriormente a un hombre sordo, Alexander Popham, a hablar "clara y claramente, y con un tono bueno y elegante". Más tarde, Wallis se atribuyó el mérito de esto, lo que llevó a Holder a acusar a Wallis de "saquear a sus vecinos y adornarse con sus spoyls".

Wallis' nombramiento como Profesor Savilian de Geometría en la Universidad de Oxford

La visita parlamentaria de Oxford que comenzó en 1647 destituyó a muchos académicos de alto nivel de sus puestos, incluidos (en noviembre de 1648) los profesores Savilian de geometría y astronomía. En 1649, Wallis fue nombrado profesor Savilian de Geometría. Wallis parece haber sido elegido en gran parte por motivos políticos (como quizás lo había sido su predecesor realista Peter Turner, quien a pesar de su nombramiento para dos cátedras nunca publicó ningún trabajo matemático); Si bien Wallis fue quizás el criptógrafo líder de la nación y formó parte de un grupo informal de científicos que luego se convertiría en la Royal Society, no tenía una reputación particular como matemático. No obstante, Wallis' el nombramiento resultó ampliamente justificado por su trabajo posterior durante los 54 años que se desempeñó como profesor Savilian.

Contribuciones a las matemáticas

Ópera matemática, 1699

Wallis hizo importantes contribuciones a la trigonometría, el cálculo, la geometría y el análisis de series infinitas. En su Opera Mathematica I (1695) introdujo el término "fracción continua".

Geometría analítica

En 1655, Wallis publicó un tratado sobre las secciones cónicas en el que las definía analíticamente. Este fue el primer libro en el que estas curvas se consideran y definen como curvas de segundo grado. Ayudó a eliminar parte de la dificultad y oscuridad percibidas de René Descartes' trabajar en geometría analítica. En el Tratado sobre las secciones cónicas, Wallis popularizó el símbolo ∞ para el infinito. Escribió: "Supongo que cualquier plano (siguiendo la Geometría de los Indivisibles de Cavalieri) está formado por un número infinito de líneas paralelas, o como yo preferiría, por un número infinito de paralelogramos de la misma altura; (sea la altura de cada uno de estos una parte infinitamente pequeña 1/∞ de la altura total, y deje que el símbolo ∞ denote Infinito) y la altura de todos para formar la altura de la figura."

Cálculo integral

Arithmetica Infinitorum, la más importante de las obras de Wallis, se publicó en 1656. En este tratado se sistematizaban y ampliaban los métodos de análisis de Descartes y Cavalieri, pero quedaban abiertas algunas ideas. a la critica Comenzó, después de un breve tratado sobre secciones cónicas, desarrollando la notación estándar para potencias, ampliándolas de enteros positivos a números racionales:

{displaystyle x^{0}=1}

{displaystyle x^{-1}={frac {1}{x}}}

{displaystyle x^{-n}={frac {1}{x^{n}}}{text{ etc.}}}

{displaystyle x^{1/2}={sqrt {x}}}

{displaystyle x^{2/3}={sqrt[{3}]{x^{2}}}{text{ etc.}}}

{displaystyle x^{1/n}={sqrt[{n}]{x}}}

{displaystyle x^{p/q}={sqrt[{q}]{x^{p}}}}

Dejando las numerosas aplicaciones algebraicas de este descubrimiento, procedió a encontrar, por integración, el área encerrada entre la curva y = x^m, eje x y cualquier ordenada x = h, y demostró que la razón de este el área a la del paralelogramo en la misma base y de la misma altura es 1/(m + 1), extendiendo la fórmula de cuadratura de Cavalieri. Aparentemente asumió que el mismo resultado también sería cierto para la curva y = ax^m, donde a es cualquier constante, y m cualquier número positivo o negativo, pero discutió solo el caso de la parábola en la que m = 2 y la hipérbola en que m = −1. En este último caso, su interpretación del resultado es incorrecta. Luego demostró que se pueden escribir resultados similares para cualquier curva de la forma

{displaystyle y=sum _{m}^{}ax^{m}}

y por tanto que, si la ordenada y de una curva se puede expandir en potencias de x, se puede determinar su área: así dice que si la ecuación de la curva es y = x⁰ + x¹ + x ² +..., su área sería x + x²/2 + x ³/3 +... . Luego aplicó esto a la cuadratura de las curvas y = (x − x²)⁰, y = (x − x²)¹, y = (x − x²)², etc., tomado entre los límites x = 0 y x = 1. Muestra que las áreas son, respectivamente, 1, 1/6, 1/30, 1/140, etc. Luego consideró curvas de la forma y = x^1/m y estableció el teorema de que el área delimitada por esta curva y las líneas x = 0 y x = 1 es igual al área del rectángulo en la misma base y de la misma altura que m: m + 1. Esto es equivalente a calcular

{displaystyle int _{0}^{1}x^{1/m},dx.}

Ilustró esto con la parábola, en cuyo caso m = 2. Declaró, pero no probó, el resultado correspondiente para una curva de la forma y = x^p/q.

Wallis mostró una ingenuidad considerable en la reducción de las ecuaciones de curvas a las formas dadas anteriormente, pero, como no estaba familiarizado con el teorema binomio, no podía afectar la cuadratura del círculo, cuya ecuación es $y={sqrt {1-x^{2}}}$ , ya que no pudo expandir esto en poderes de x. Sin embargo, establece el principio de la interpolación. Así, como el ordeno del círculo $y={sqrt {1-x^{2}}}$ es la media geométrica de los ordenados de las curvas $y=(1-x^{2})^{0}$ y $y=(1-x^{2})^{1}$ , se podría suponer que, como aproximación, el área del semicírculo ${displaystyle int _{0}^{1}!{sqrt {1-x^{2}}},dx}$ que es ${tfrac {1}{4}}pi$ puede ser tomado como la media geométrica de los valores

{displaystyle int _{0}^{1}(1-x^{2})^{0},dx {text{ and }}int _{0}^{1}(1-x^{2})^{1},dx,}

es decir, $1$ y ${tfrac {2}{3}}$ ; esto equivale a tomar ${displaystyle 4{sqrt {tfrac {2}{3}}}}$ o 3.26... como el valor de π. Pero, Wallis argumentó, de hecho tenemos una serie ${displaystyle 1,{tfrac {1}{6}},{tfrac {1}{30}},{tfrac {1}{140}},}$ ... y por lo tanto el término interpolado entre $1$ y $tfrac{1}{6}$ Debe ser elegido para obedecer la ley de esta serie. Esto, por un método elaborado que no se describe en detalle, conduce a un valor para el término interpolado que es equivalente a tomar

{displaystyle {frac {pi }{2}}={frac {2}{1}}cdot {frac {2}{3}}cdot {frac {4}{3}}cdot {frac {4}{5}}cdot {frac {6}{5}}cdot {frac {6}{7}}cdots }

(que ahora se conoce como el producto de Wallis).

En este trabajo también se analizan la formación y las propiedades de las fracciones continuas, tema que se ha destacado por el uso de estas fracciones por parte de Brouncker.

Pocos años después, en 1659, Wallis publicó un tratado que contenía la solución de los problemas sobre la cicloide que había propuesto Blaise Pascal. En esto, de paso, explicó cómo los principios establecidos en su Arithmetica Infinitorum podrían usarse para la rectificación de curvas algebraicas y dio una solución al problema de rectificar (es decir, encontrar la longitud de) la parábola semicúbica. x³ = ay², que había sido descubierto en 1657 por su alumno William Neile. Dado que todos los intentos de rectificar la elipse y la hipérbola habían sido (necesariamente) ineficaces, se supuso que ninguna curva podía rectificarse, como de hecho Descartes había afirmado definitivamente que era el caso. La espiral logarítmica había sido rectificada por Evangelista Torricelli y fue la primera línea curva (aparte del círculo) cuya longitud se determinó, pero la extensión de Neile y Wallis a una curva algebraica fue novedosa. La cicloide fue la siguiente curva rectificada; esto fue hecho por Christopher Wren en 1658.

A principios de 1658, van Heuraët hizo un descubrimiento similar, independiente del de Neile, y fue publicado por van Schooten en su edición de Geometria de Descartes en 1659. Van El método de Heuraët es el siguiente. Supone que la curva está referida a ejes rectangulares; si esto es así, y si (x, y) son las coordenadas de cualquier punto sobre él, y n es la longitud de la normal, y si se toma otro punto cuyas coordenadas son (x, η) tal que η: h = n: y, donde h es una constante; entonces, si ds es el elemento de la longitud de la curva requerida, tenemos por triángulos semejantes ds: dx = n: y. Por lo tanto, h ds = η dx. Por lo tanto, si se puede encontrar el área del lugar geométrico del punto (x, η), la primera curva se puede rectificar. De esta manera van Heuraët efectuó la rectificación de la curva y³ = ax² pero añadió que la rectificación de la parábola y² = ax es imposible ya que requiere la cuadratura de la hipérbola. Las soluciones dadas por Neile y Wallis son algo similares a las dadas por van Heuraët, aunque no se enuncia una regla general y el análisis es torpe. Fermat sugirió un tercer método en 1660, pero es poco elegante y laborioso.

Colisión de cuerpos

La teoría de la colisión de cuerpos fue propuesta por la Royal Society en 1668 para la consideración de los matemáticos. Wallis, Christopher Wren y Christiaan Huygens enviaron soluciones correctas y similares, todas dependiendo de lo que ahora se llama conservación del impulso; pero, mientras que Wren y Huygens limitaron su teoría a los cuerpos perfectamente elásticos (colisión elástica), Wallis consideró también los cuerpos imperfectamente elásticos (colisión inelástica). Esto fue seguido en 1669 por un trabajo sobre estática (centros de gravedad), y en 1670 por uno sobre dinámica: estos proporcionan una sinopsis conveniente de lo que entonces se sabía sobre el tema.

Álgebra

En 1685 Wallis publicó Álgebra, precedida de un relato histórico del desarrollo de la materia, que contiene una gran cantidad de información valiosa. La segunda edición, publicada en 1693 y que forma el segundo volumen de su Opera, se amplió considerablemente. Esta álgebra es notable por contener el primer uso sistemático de fórmulas. Una magnitud dada se representa aquí por la relación numérica que guarda con la unidad del mismo tipo de magnitud: así, cuando Wallis quiere comparar dos longitudes, considera que cada una contiene tantas unidades de longitud. Esto quizás quede más claro al notar que la relación entre el espacio descrito en cualquier tiempo por una partícula que se mueve con una velocidad uniforme es denotada por Wallis por la fórmula

s = vt,

donde s es el número que representa la relación entre el espacio descrito y la unidad de longitud; mientras que los escritores anteriores habrían denotado la misma relación declarando lo que es equivalente a la proposición

s₁: s₂ = v₁t₁: v₂t₂.

Renglón numérico

Refiriéndose a avanzar y retirarse desde el punto

A

Wallis escribió Un tratado de álgebra que...

-3

doth como realmente el diseño del punto

D

; como

{displaystyle +3}

diseñado el punto

C

... Y cada diseño (al menos en la misma Línea Infinita) un punto único: Y sólo uno".

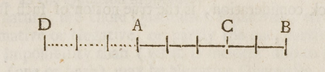
Wallis ha sido acreditado como el creador de la recta numérica "para cantidades negativas" y "para fines operativos". Esto se basa en un pasaje de su tratado de álgebra de 1685 en el que introdujo una recta numérica para ilustrar la legitimidad de las cantidades negativas:

Sin embargo, no es esa Suposición (de Cuantidades Negativas) o Inútil o Absurdo; cuando se entiende correctamente. Y sin embargo, en cuanto a la noción álgebraica desnuda, importa una Cantidad menos que nada: Sin embargo, cuando se trata de una Aplicación Física, denota como Real una Cantidad como si la Señal fuera $+$ ; pero ser interpretado en sentido contrario... ${displaystyle +3}$ , significa $3$ Yards Forward; and $-3$ , significa $3$ Yards Backward.

También se ha observado que, en un trabajo anterior, Wallis llegó a la conclusión de que la proporción de un número positivo a uno negativo es mayor que el infinito. El argumento implica el cociente ${displaystyle {tfrac {1}{x}}}$ y considerando lo que sucede como $x$ y luego cruza el punto $x=0$ del lado positivo. Wallis no estaba solo en este pensamiento: Leonhard Euler llegó a la misma conclusión considerando la serie geométrica ${displaystyle {tfrac {1}{1-x}}=1+x+x^{2}+cdots }$ , evaluado en $x=2$ , seguido de razonamiento similar al de Wallis (resolvió la paradoja distinguiendo diferentes tipos de números negativos).

Geometría

Por lo general, se le atribuye la demostración del teorema de Pitágoras utilizando triángulos semejantes. Sin embargo, Thabit Ibn Qurra (901 dC), un matemático árabe, había producido una generalización del teorema de Pitágoras aplicable a todos los triángulos seis siglos antes. Es una conjetura razonable que Wallis estuviera al tanto del trabajo de Thabit.

Wallis también se inspiró en las obras del matemático islámico Sadr al-Tusi, hijo de Nasir al-Din al-Tusi, particularmente en el libro de al-Tusi escrito en 1298 sobre el postulado paralelo. El libro se basó en los pensamientos de su padre y presentó uno de los primeros argumentos para una hipótesis no euclidiana equivalente al postulado paralelo. Después de leer esto, Wallis luego escribió sobre sus ideas mientras desarrollaba sus propios pensamientos sobre el postulado, tratando de demostrarlo también con triángulos semejantes.

Descubrió que el quinto postulado de Euclides es equivalente al que actualmente se denomina "postulado de Wallis" despues de el. Este postulado establece que "Sobre una línea recta finita dada siempre es posible construir un triángulo similar a un triángulo dado". Este resultado estaba englobado en una tendencia que intentaba deducir la quinta de Euclides a partir de los otros cuatro postulados que hoy se sabe que es imposible. A diferencia de otros autores, se dio cuenta de que los cuatro primeros postulados no garantizaban el crecimiento ilimitado de un triángulo.

Calculadora

Otro aspecto de las habilidades matemáticas de Wallis era su habilidad para hacer cálculos mentales. Dormía mal ya menudo hacía cálculos mentales mientras yacía despierto en su cama. Una noche calculó mentalmente la raíz cuadrada de un número de 53 cifras. Por la mañana dictó la raíz cuadrada de 27 dígitos del número, todavía enteramente de memoria. Fue una hazaña que se consideró notable, y Henry Oldenburg, el secretario de la Royal Society, envió a un colega a investigar cómo lo hizo Wallis. Se consideró lo suficientemente importante como para merecer una discusión en las Transacciones filosóficas de la Royal Society de 1685.

Teoría musical

Wallis tradujo al latín obras de Ptolomeo y Bryennius, y el comentario de Porfirio sobre Ptolomeo. También publicó tres cartas a Henry Oldenburg sobre la afinación. Aprobó el temperamento igual, que estaba siendo utilizado en los órganos de Inglaterra.

Otras obras

Ópera matemática, 1657

Su Institutio logicae, publicada en 1687, fue muy popular. La Grammatica linguae Anglicanae fue una obra sobre la gramática inglesa, que permaneció impresa hasta bien entrado el siglo XVIII. También publicó sobre teología.

Contenido relacionado

Más resultados...