Johnson, que estuvo a punto de estrellarse, es sólido
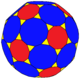
En geometría, un sólido de Johnson casi convexo es un poliedro estrictamente convexo cuyas caras están cerca de ser polígonos regulares, pero algunas o todas ellas no son precisamente regulares. Por lo tanto, no cumple con la definición de un sólido de Johnson, un poliedro cuyas caras son todas regulares, aunque "a menudo se puede construir físicamente sin notar la discrepancia" entre sus caras regulares e irregulares. El número preciso de casi convexos depende de qué tan cerca se requiere que las caras de dicho poliedro se aproximen a los polígonos regulares.
Algunos de los casi errores con alta simetría también son simetroedros con algunas caras de polígonos verdaderamente regulares.
Algunos de los que se encuentran cerca de un accidente también son zonohedros.
Ejemplos
| Nombre Nombre de Conway | Imagen | Vertexconfigurations | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | F12 | Simmetría |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Associahedron t4dP3 |  | 2 (5.5.5) 12 (4.5.5) | 14 | 21 | 9 | 3 | 6 | Dih3 Orden 12 | |||||
| Truncated triakis tetrahedron t6kT |  | 4 (5.5.5) 24 (5.5.6) | 28 | 42 | 16 | 12 | 4 | Td[3,3] Orden 24 | |||||
| Pentahexagonal pyritoheptacontatetraedro |  | 12 (3.5.3.6) 24 (3.3.5.6) 24 (3.3.3.5) | 60 | 132 | 74 | 56 | 12 | 6 | Th[3]+4] Orden 24 | ||||
| Cubo de Chamfer cC |  | 24 (4.6.6) 8 (6.6.6) | 32 | 48 | 18 | 6 | 12 | Oh[4,3] Orden 48 | |||||
| -- |  | 12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) | 30 | 54 | 26 | 12 | 12 | 2 | D6h, [6,2] Orden 24 | ||||
| -- |  | 6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) | 27 | 51 | 26 | 14 | 12 | D3h[3,2] Orden 12 | |||||
| Tetrated dodecahedron |  | 4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) | 28 | 54 | 28 | 16 | 12 | Td[3,3] Orden 24 | |||||
| Chamfered dodecahedron cD |  | 60 (5.6.6) 20 (6.6.6) | 80 | 120 | 42 | 12 | 30 | Ih[5,3] Orden 120 | |||||
| Rectificado icosahedro truncado atl |  | 60 (3.5.3.6) 30 (3.6.3.6) | 90 | 180 | 92 | 60 | 12 | 20 | Ih[5,3] Orden 120 | ||||
| Truncated icosahedron tt |  | 120 (3.10.12) 60 (3.12.12) | 180 | 270 | 92 | 60 | 12 | 20 | Ih[5,3] Orden 120 | ||||
| Ampliación de icosahedron truncado et I |  | 60 (3.4.5.4) 120 (3.4.6.4) | 180 | 360 | 182 | 60 | 90 | 12 | 20 | Ih[5,3] Orden 120 | |||
| Snub rectified truncated icosahedron stI |  | 60 (3.3.3.5) 120 (3.3.3.6) | 180 | 450 | 272 | 240 | 12 | 20 | I[5,3]+ Orden 60 |
Errores coplanares
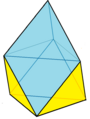
Algunos sólidos de Johnson que no se han aprobado tienen caras coplanares. Estos poliedros pueden ser perturbados para volverse convexos con caras que están arbitrariamente cerca de los polígonos regulares. Estos casos utilizan figuras de vértice 4.4.4.4 del mosaico cuadrado, figuras de vértice 3.3.3.3.3.3 del mosaico triangular, así como caras de triángulos equiláteros dobles divididos por rombos de 60 grados, o un trapezoide de 60 grados como tres triángulos equiláteros. Es posible tomar una cantidad infinita de errores coplanares distintos de secciones del panal cúbico (alternativamente policubos convexos) o panal cúbico alternado, ignorando cualquier cara oscurecida.
Ejemplos: 3.3.3.3.3.3
El prisma romábico
Wedge
Trigonal trapezohedron
pirámide trigonal Gyroelongated
Triangulado monorectified tetrahedron
Elongated octahedron
Tetratetraedro, triangulado tetraedro
Cupola triangular aumentada
Bipirámide triangular triangulado
Edge-contractedron
Prisma hexagonal
Antiprismos hexagonal,
pirámide hexagonal
Triangular cupola
Truncated tetrahedron
Truncado octaedro
4.4.4.4
Square icositetraedron
(Cube)
3.4.6.4:
Cupola hexagonal
(Degenerado)
