James Gregory (matemático)

James Gregory FRS (noviembre de 1638 - octubre de 1675) fue un matemático y astrónomo escocés. Su apellido a veces se escribe como Gregorie, la ortografía escocesa original. Describió uno de los primeros diseños prácticos para el telescopio reflector, el telescopio gregoriano, e hizo avances en trigonometría, descubriendo representaciones de series infinitas para varias funciones trigonométricas.

En su libro Geometriae Pars Universalis (1668) Gregory dio tanto el primer enunciado publicado como la prueba del teorema fundamental del cálculo (enunciado desde un punto de vista geométrico, y solo para una clase especial de las curvas consideradas por versiones posteriores del teorema), por lo que fue reconocido por Isaac Barrow.

Biografía

Gregory nació en 1638. Su madre, Janet, era hija de Jean y David Anderson, y su padre, John Gregory, un ministro de la Iglesia Episcopal de Escocia. James era el menor de sus tres hijos y nació en la rectoría de Drumoak., Aberdeenshire, e inicialmente fue educado en casa por su madre, Janet Anderson (~1600–1668). Fue su madre quien dotó a Gregory de su apetito por la geometría, su tío, Alexander Anderson (1582-1619), había sido alumno y editor del matemático francés Viète. Después de la muerte de su padre en 1651, su hermano mayor, David, se hizo cargo de su educación. Asistió a Aberdeen Grammar School y luego a Marischal College de 1653 a 1657, y se graduó AM en 1657.

En 1663 viajó a Londres y se reunió con John Collins y su compatriota escocés Robert Moray, uno de los fundadores de la Royal Society. En 1664 partió hacia la Universidad de Padua, en la República de Venecia, pasando por Flandes, París y Roma en su camino. En Padua vivió en la casa de su compatriota James Caddenhead, el profesor de filosofía, y fue instruido por Stefano Angeli.

A su regreso a Londres en 1668, fue elegido miembro de la Royal Society, antes de viajar a St. Andrews a fines de 1668 para asumir su cargo como primer profesor Regius de Matemáticas en la Universidad de St. Andrews, cargo creado para él por Carlos II, probablemente a petición de Roberto Moray. Allí, en la Universidad de St Andrews, colocó la primera línea del meridiano en el suelo de su laboratorio en 1673, 200 años antes de que se estableciera el meridiano de Greenwich, y por lo tanto "podría decirse que St Andrews es el lugar donde comenzó el tiempo". #34;.

Fue sucesivamente profesor en la Universidad de St Andrews y en la Universidad de Edimburgo.

Se había casado con Mary, hija de George Jameson, pintor y viuda de John Burnet de Elrick, Aberdeen; su hijo James fue profesor de física en King's College, Aberdeen. Fue el abuelo de John Gregory (FRS 1756); tío de David Gregorie (FRS 1692) y hermano de David Gregory (1627–1720), médico e inventor.

Alrededor de un año después de asumir la cátedra de Matemáticas en Edimburgo, James Gregory sufrió un derrame cerebral mientras observaba las lunas de Júpiter con sus alumnos. Murió unos días después a la edad de 36 años.

Obras publicadas

Vera circuli et hyperbolae quadratura, 1667

Óptica Promota

En la Optica Promota, publicada en 1663, Gregory describió su diseño para un telescopio reflector, el "telescopio gregoriano". También describió el método para usar el tránsito de Venus para medir la distancia de la Tierra al Sol, que más tarde fue defendido por Edmund Halley y adoptado como base de la primera medición efectiva de la Unidad Astronómica.

Vera Circuli et Hyperbolae Quadratura

Antes de dejar Padua, Gregory publicó Vera Circuli et Hyperbolae Quadratura (1667) en el que aproximaba las áreas del círculo y la hipérbola con series convergentes:

[James Gregory] no se puede negar la autoría de muchos teoremas curiosos sobre la relación del círculo con los polígonos inscritos y circunscritos, y su relación entre sí. Por medio de estos teoremas da con infinitamente menos problemas que por los cálculos habituales,... la medida del círculo e hiperbola (y consecuentemente la construcción de logaritmos) a más de veinte lugares decimales. Siguiendo el ejemplo de Huygens, también dio construcciones de líneas rectas iguales a los arcos del círculo, y cuyo error es aún menor.

"La primera demostración del teorema fundamental del cálculo y el descubrimiento de la serie de Taylor se le pueden atribuir."

El libro se reimprimió en 1668 con un apéndice, Geometriae Pars, en el que Gregory explicaba cómo se podían determinar los volúmenes de sólidos de revolución.

Telescopio gregoriano

Diagrama de un telescopio reflector gregoriano.

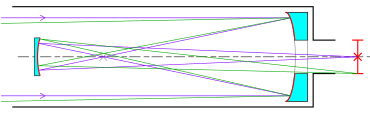
En su Optica Promota de 1663, James Gregory describió su telescopio reflector, que se conoce con su nombre, el telescopio gregoriano. Gregory señaló que un telescopio reflector con un espejo parabólico corregiría la aberración esférica así como la aberración cromática que se observa en los telescopios refractores. En su diseño, también colocó un espejo secundario cóncavo con una superficie elíptica más allá del punto focal del espejo primario parabólico, reflejando la imagen a través de un orificio en el espejo primario donde podía verse convenientemente. Según su propia confesión, Gregory no tenía ninguna habilidad práctica y no pudo encontrar ningún óptico capaz de construir uno.

El diseño del telescopio atrajo la atención de varias personas en el establecimiento científico, como Robert Hooke, el físico de Oxford que finalmente construyó el telescopio 10 años después, y Sir Robert Moray, erudito y miembro fundador de la Royal Society.

El diseño del telescopio gregoriano rara vez se usa en la actualidad, ya que se sabe que otros tipos de telescopios reflectores son más eficientes para aplicaciones estándar. La óptica gregoriana también se utiliza en radiotelescopios como el de Arecibo, que cuenta con una "cúpula gregoriana".

Matemáticas

El siguiente extracto es de la Pantologia. Una nueva cyclopædia (gabinete) (1813)

El Sr. James Gregory era un hombre de un genio muy agudo y penetrante... La parte más brillante de su personaje fue la de su genio matemático como un inventor, que fue de la primera orden; como aparecerá por... sus invenciones y descubrimientos [que incluyen] la cuadrícula del círculo e hiperbola, por una serie infinita convergente; su método para la transformación de las curvas; una demostración geométrica de la serie de Lord Brouncker para cubrir la hiperbola — su demostración de que la línea meridiana es ana Estos, con otros, para medir la longitud de las curvas elípticas e hiperbólicas, fueron enviados al Sr. Collins, a cambio de algunos recibidos de él de Newton, en el que siguió el ejemplo elegante de este autor, al entregar su serie en términos simples, independientes entre sí.

Otro trabajo

En una carta de 1671 a John Collins, Gregory da la expansión de la serie de potencia de las siete funciones (utilizando la notación moderna) arctan⁡ ⁡ x{textstyle arctan x} (a menudo llamada serie de Gregory), #⁡ ⁡ x,{textstyle tan x,} sec⁡ ⁡ x,{textstyle sec x,} logsec⁡ ⁡ x,{textstyle log ,sec x,} la inversa función Gudermanniana log#⁡ ⁡ 12()x+12π π ){textstyle log ,tan {tfrac {1}{2}{bigl (}x+{tfrac {1}pi {bigr)}}}, arcsec⁡ ⁡ ()2ex),{textstyle operatorname {arcsec} {bigl (}{sqrt {2}e^{x}{bigr)}}} y la función Gudermanniana 2arctan⁡ ⁡ ex− − 12π π .{textstyle 2arctan e^{x}-{tfrac {1} {2}pi.}

Existe evidencia de que descubrió el método de tomar derivadas superiores para calcular una serie de potencias, que no fue descubierto por Taylor hasta 1715, pero no publicó sus resultados, pensando que solo había redescubierto 'Mr. método universal de Newton, " que se basaba en una técnica diferente.

James Gregory descubrió la rejilla de difracción haciendo pasar la luz del sol a través de una pluma de pájaro y observando el patrón de difracción producido. En particular, observó la división de la luz solar en los colores que la componen; esto ocurrió un año después de que Newton hiciera lo mismo con un prisma y el fenómeno aún era muy controvertido.

Una rueda redonda no es adecuada para superficies irregulares y Gregory ideó una "rueda adaptable" utilizando una transformación de Gregory.

Gregory, un partidario entusiasta de Newton, luego mantuvo mucha correspondencia amistosa con él e incorporó sus ideas a su propia enseñanza, ideas que en ese momento eran controvertidas y consideradas bastante revolucionarias.

El cráter Gregory en la Luna lleva su nombre. Era tío del matemático David Gregory.

Obras

• 1663 – Optica promota (El avance de la óptica), enlace de Google Books.
• 1667 – Vera circuli et hyperbolae quadratura (El verdadero squaring del círculo e hiperbola) vía Archivo de Internet
• 1668 – Ejercicios geométricos (ejercicios geométricos), enlace de Google Books.
• 1668 – Geometriae pars universalis (La parte universal de la geometría)