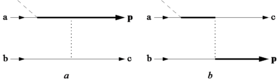Ionización

El viento solar que pasa por la magnetosfera altera los movimientos de partículas cargadas en la termosfera o la exosfera de la Tierra, y el consiguiente ionización de estas partículas las hace emitir luz de color variable, formando así auroras cerca de las regiones polares.

Ionización, o ionización es el proceso por el cual un átomo o una molécula adquiere una carga negativa o positiva al ganar o perder electrones, a menudo junto con otros cambios químicos. El átomo o molécula cargado eléctricamente resultante se llama ion. La ionización puede resultar de la pérdida de un electrón después de colisiones con partículas subatómicas, colisiones con otros átomos, moléculas e iones, o mediante la interacción con la radiación electromagnética. Las reacciones de escisión de enlaces heterolíticos y de sustitución heterolítica pueden dar como resultado la formación de pares de iones. La ionización puede ocurrir a través de la desintegración radiactiva por el proceso de conversión interna, en el que un núcleo excitado transfiere su energía a uno de los electrones de la capa interna y hace que sea expulsado.

Usos

Ejemplos cotidianos de ionización de gas son, por ejemplo, dentro de una lámpara fluorescente u otras lámparas de descarga eléctrica. También se utiliza en detectores de radiación como el contador Geiger-Müller o la cámara de ionización. El proceso de ionización se usa ampliamente en una variedad de equipos en ciencia fundamental (p. ej., espectrometría de masas) y en la industria (p. ej., radioterapia).

Producción de iones

Efecto de Avalanche en un campo eléctrico creado entre dos electrodos. El evento de ionización original libera un electrón, y cada colisión posterior libera un electron adicional, por lo que dos electrones emergen de cada colisión: el electron ionizante y el electron liberado.

Los iones cargados negativamente se producen cuando un electrón libre choca con un átomo y, posteriormente, queda atrapado dentro de la barrera de potencial eléctrico, liberando el exceso de energía. El proceso se conoce como ionización por captura de electrones.

Los iones cargados positivamente se producen transfiriendo una cantidad de energía a un electrón unido en una colisión con partículas cargadas (por ejemplo, iones, electrones o positrones) o con fotones. La cantidad umbral de la energía requerida se conoce como potencial de ionización. El estudio de tales colisiones es de fundamental importancia con respecto al problema de los pocos cuerpos, que es uno de los principales problemas no resueltos de la física. Los experimentos cinemáticamente completos, es decir, experimentos en los que se determina el vector de momento completo de todos los fragmentos de colisión (el proyectil disperso, el ion objetivo en retroceso y el electrón expulsado), han contribuido a avances importantes en la comprensión teórica del problema de los pocos cuerpos. en años recientes.

Ionización adiabática

La ionización adiabática es una forma de ionización en la que se extrae o se agrega un electrón a un átomo o molécula en su estado de energía más bajo para formar un ion en su estado de energía más bajo.

La descarga de Townsend es un buen ejemplo de la creación de iones positivos y electrones libres debido al impacto de iones. Es una reacción en cascada que involucra electrones en una región con un campo eléctrico suficientemente alto en un medio gaseoso que puede ionizarse, como el aire. Después de un evento de ionización original, debido a una radiación ionizante, el ion positivo se desplaza hacia el cátodo, mientras que el electrón libre se desplaza hacia el ánodo del dispositivo. Si el campo eléctrico es lo suficientemente fuerte, el electrón libre gana suficiente energía para liberar un electrón adicional cuando choca con otra molécula. Luego, los dos electrones libres viajan hacia el ánodo y obtienen suficiente energía del campo eléctrico para causar la ionización por impacto cuando ocurran las próximas colisiones; etcétera. Esto es efectivamente una reacción en cadena de generación de electrones y depende de que los electrones libres obtengan suficiente energía entre colisiones para sostener la avalancha.

La eficiencia de ionización es la relación entre la cantidad de iones formados y la cantidad de electrones o fotones utilizados.

Energía de ionización de los átomos

Energías de ionización de elementos neutrales (predecidos más allá de 104)

La tendencia en la energía de ionización de los átomos se usa a menudo para demostrar el comportamiento periódico de los átomos con respecto al número atómico, como se resume al ordenar los átomos en la tabla de Mendeleev. Esta es una herramienta valiosa para establecer y comprender el orden de los electrones en los orbitales atómicos sin entrar en los detalles de las funciones de onda o el proceso de ionización. En la figura de la derecha se presenta un ejemplo. La disminución abrupta periódica en el potencial de ionización después de los átomos de gases raros, por ejemplo, indica la aparición de una nueva capa en los metales alcalinos. Además, los máximos locales en el gráfico de energía de ionización, moviéndose de izquierda a derecha en una fila, son indicativos de las subcapas s, p, d y f.

Descripción semiclásica de la ionización

La física clásica y el modelo atómico de Bohr pueden explicar cualitativamente la fotoionización y la ionización mediada por colisión. En estos casos, durante el proceso de ionización, la energía del electrón supera la diferencia de energía de la barrera de potencial que intenta atravesar. La descripción semiclásica, sin embargo, no puede describir la ionización de túnel ya que el proceso implica el paso de electrones a través de una barrera de potencial clásicamente prohibida.

Descripción mecánica cuántica de la ionización

La interacción de átomos y moléculas con pulsos de láser lo suficientemente fuertes conduce a la ionización de iones con carga simple o múltiple. La tasa de ionización, es decir, la probabilidad de ionización en la unidad de tiempo, solo se puede calcular utilizando la mecánica cuántica. En general, las soluciones analíticas no están disponibles y las aproximaciones requeridas para cálculos numéricos manejables no brindan resultados lo suficientemente precisos. Sin embargo, cuando la intensidad del láser es lo suficientemente alta, la estructura detallada del átomo o molécula puede ignorarse y es posible una solución analítica para la tasa de ionización.

Ionización de túnel

Potencial combinado de un átomo y un campo láser uniforme. A distancias r. r₀, el potencial del láser se puede descuidar, mientras que a distancias con r ■ r₀ el potencial Coulomb es insignificante en comparación con el potencial del campo láser. El electrón emerge de debajo de la barrera r = R_c. E_i es el potencial de ionización del átomo.

La ionización de túnel es la ionización debida a la tunelización cuántica. En la ionización clásica, un electrón debe tener suficiente energía para atravesar la barrera de potencial, pero el túnel cuántico permite que el electrón simplemente atraviese la barrera de potencial en lugar de atravesarla por completo debido a la naturaleza ondulatoria del electrón. La probabilidad de que un electrón pase a través de la barrera cae exponencialmente con el ancho de la barrera de potencial. Por lo tanto, un electrón con una energía más alta puede hacer que supere la barrera potencial, dejando una barrera mucho más delgada para atravesar y, por lo tanto, una mayor posibilidad de hacerlo. En la práctica, la ionización de túnel es observable cuando el átomo o la molécula interactúan con fuertes pulsos de láser en el infrarrojo cercano. Este proceso puede entenderse como un proceso por el cual se ioniza un electrón acotado, a través de la absorción de más de un fotón del campo láser. Esta imagen se conoce generalmente como ionización multifotónica (MPI).

Keldysh modeló el proceso MPI como una transición del electrón del estado fundamental del átomo a los estados de Volkov. En este modelo se desprecia la perturbación del estado fundamental por el campo láser y no se tienen en cuenta los detalles de la estructura atómica al determinar la probabilidad de ionización. La mayor dificultad con el modelo de Keldysh fue su descuido de los efectos de la interacción de Coulomb en el estado final del electrón. Como se observa en la figura, el campo de Coulomb no es de magnitud muy pequeña en comparación con el potencial del láser a distancias mayores del núcleo. Esto contrasta con la aproximación realizada al despreciar el potencial del láser en las regiones cercanas al núcleo. Perelomov et al. incluyó la interacción de Coulomb a distancias internucleares más grandes. Su modelo (que llamamos modelo PPT) se derivó para un potencial de corto alcance e incluye el efecto de la interacción de Coulomb de largo alcance a través de la corrección de primer orden en la acción casi clásica. Larochelle et al. han comparado las curvas de iones versus intensidad predichas teóricamente de átomos de gases raros que interactúan con un láser Ti:Sapphire con mediciones experimentales. Han demostrado que la tasa de ionización total predicha por el modelo PPT se ajusta muy bien a los rendimientos de iones experimentales para todos los gases raros en el régimen intermedio del parámetro de Keldysh.

La tasa de MPI en átomo con potencial de ionización ${displaystyle E_{i}$ en un láser polarizado linealmente con frecuencia ${displaystyle omega }$ es dado por

${displaystyle W_{T}=left habitC_{*}l^{*}}right perpetua^{2}{sqrt {fnK} {fnMicroc} {fnMicroc} {fnMicroc} {fn} {fn} {fnMicroc} {fn}} {fn} {fnMicroc}} {f} {fnMicroc}} {fnMicroc}} {f}}} {f}} {f}f} {f}fnf}fnfnf}f}f}f}f}fnf}fnfnfnfnfnfnf}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn }f_{lm}E_{i}left({frac {2}}left(2E_{i}right){frac {3}{2}right)^{2n^{*}-Prin^{*}-Principe a la vida eterna--{frac {3}}left(1+gammamma ¿Qué? {m}{2} 'justo en la vida+{frac} {3} {4}}A_{m}(omegagamma)e^{-{-{frac {2}{F}left(2E_{i}right)}{frac {3} {2}gleft(gammaright)}}}}}}}}}$

dónde

• ${displaystyle gamma ={frac ################################################################################################################################################################################################################################################################ {2E_{i}}} {F}}} {f}} {f}}}} {f}}}}} {f}}}}}} {f}}}}}} {f}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}} {}}} {}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ es el parámetro de adiabaticidad de Keldysh,
• ${displaystyle n^{*}={frac} { sqrt {2E_{i}} {Z^{2}}} {f}} {f}}}} {f}}}} {f}}}}}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$,
• ${displaystyle F}$ es el campo eléctrico pico del láser y
• ${displaystyle l^{*}=n^{*}-1}$.

Los coeficientes ${displaystyle f_{lm}$, ${displaystyle g(gamma)}$ y ${displaystyle C_{}l^{*}}}$ son dados por

${begin{aligned}f_{lm} {frac {(2l+1)(I+ tuviendo)}{2}{2^{m} turbación!(l- turba la vida)}g(g(gamma)}={2gamma}{2}{}{0}{0}{0}{0}{0}{0}}}}} {}}}}}}}}}} { {1+gamma ¿Qué? {2^{2n^{*} {fn} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn}} {fn}} {fn}}}}}}} {\\fn}}}} {\fn}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\ Gamma (n^{*}+l^{*}+1) Gamma (n^{*}-l^{*}}end{aligned}}$

El coeficiente ${displaystyle A_{m}(omegagamma)}$ es dado por

${displaystyle A_{m}(omegagamma)={frac {4}{3pi }{frac {1} {fnMientras!} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}}} {f} {f}}}{fnMicroc}}{f}}}}{fnMicrob}{f}}}{fnMicrob}}{fnMicrob}}}}}}}}}}{fnMicroc}{f}}{fnMicroc}}}}}}}{f}}{fnMicroc}}{f}{f}}}{fnMicroc}{f}}{fnMicroc}{fnMicroc}}}}}} {gamma }{2}{1+gamma ¿Qué? } {sqrt {1+gamma }} {n-v)}right)}$

dónde

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft ] {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {gamma} # {sqrt {1+gamma Bien. {E_{i}{omega }left(1+{frac {2} {gamma }right)end{aligned}}}$

Ionización de túnel cuasi-estático

El túnel cuasi estático (QST) es la ionización cuyo ritmo puede ser predicho satisfactoriamente por el modelo ADK, es decir, el límite del modelo PPT cuando ${displaystyle gamma }$ enfoques cero. La tasa de QST se da por

${displaystyle ¿Por qué? {fnK} {fnMicroc} {fnMicroc} {fnMicroc} {fn} {fn} {fnMicroc} {fn}} {fnK} {fnMicroc}} {f}} {fn} {fnMicroc}}} {f}fnf}} {f}f}f}fnfnfnfnfnfnfnfnfnfnf}f}fnfnfnfnfnfnf}fnf}fnfnfnfnfnfnfnh}fnfnfnfnfnfnfnfnfnKfnfnfnKfnfnfnfnh}}}fnfn }f_{lm}E_{i}left({frac {2}}left(2E_{i}right){frac {3}{2}right)^{2n^{*}- {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}} {fnMicroc}}} {fnMicroc} {f}} {fnMicroc}} {fnMicroc}}} {f}}}} {f}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}f}f}e^ {f} {f}f} {f} {f} {2}{3F}left(2E_{i}right) {3}{2}}}$

En comparación con ${displaystyle ¿Qué?$ la ausencia de la suma sobre n, que representan diferentes puntos de ionización del umbral (ATI), es notable.

Aproximación de campo fuerte para la tasa de ionización

Los cálculos de PPT se realizan en el calibre E, lo que significa que el campo láser se toma como ondas electromagnéticas. La tasa de ionización también se puede calcular en el indicador A, que enfatiza la naturaleza de las partículas de la luz (que absorbe múltiples fotones durante la ionización). Este enfoque fue adoptado por el modelo Krainov basado en los trabajos anteriores de Faisal y Reiss. La tasa resultante está dada por

${displaystyle W_{KRA=sum ################################################################################################################################################################################################################################################################ {n_{mathrm} {} {}} {2}} {}}}} {}}}} {}}}}} {}}}}}}} {}}}}}}}}}} {}}} {}}} {}}} {}}} {}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}$

donde:

• ${displaystyle No.$
• ${displaystyle n_{mathrm {osc} }=U_{p}/omega }$ con ${displaystyle U_{p}$ siendo la energía ponderomotiva,
• ${displaystyle No.$ es el número mínimo de fotones necesarios para ionizar el átomo,
• ${displaystyle J_{n}(u,v)}$ es la doble función Bessel,
• ${displaystyle p={sqrt {2omega (n-n_{mathrm {osc} }$
• ${f}pf}pcos(theta)}$ con ${displaystyle theta }$ el ángulo entre el impulso del electrón, p, y el campo eléctrico del láser, F,
• FT es el tridimensional Fourier transform, and
• ${displaystyle - ¿Qué?$ incorpora la corrección Coulomb en el modelo SFA.

Estabilización atómica/atrapamiento de poblaciones

Al calcular la tasa de IMP de los átomos sólo se consideran las transiciones a los estados continuos. Tal aproximación es aceptable mientras no haya resonancia multifotona entre el estado del suelo y algunos estados excitados. Sin embargo, en situación real de interacción con láseres pulsados, durante la evolución de la intensidad del láser, debido a diferentes cambios Stark del suelo y estados excitados hay una posibilidad de que algún estado excitado vaya a resonancia multifotón con el estado del suelo. Dentro de la imagen vestida del átomo, el estado de tierra vestida por ${displaystyle m}$ fotones y el estado resonante pasan por un cruce evitado a la intensidad de la resonancia ${displaystyle Yo...$. La distancia mínima, ${displaystyle V_{m}$, en el cruce evitado es proporcional a la frecuencia de Rabi generalizada, ${displaystyle Gamma (t)= Gamma _{m}I(t)^{m/2}$ Acoplar los dos estados. Según Story et al., la probabilidad de permanecer en el estado del suelo, ${displaystyle P_{g}$, se da por

${displaystyle P_{g}=exp left(-{frac {2pi ¿Qué? ¿Qué?$

Donde ${displaystyle W.$ es la diferencia energética dependiente del tiempo entre los dos estados vestidos. En interacción con un pulso corto, si la resonancia dinámica se alcanza en el aumento o la parte caída del pulso, la población prácticamente permanece en el estado del suelo y el efecto de las resonancias multifotonales puede ser descuidado. Sin embargo, si los estados van a la resonancia en el pico del pulso, donde ${displaystyle mathrm {d} W/mathrm {d} t=0}$, entonces el estado excitado está poblado. Después de ser poblada, ya que el potencial de ionización del estado excitado es pequeño, se espera que el electrón se ionizará instantáneamente.

En 1992, de Boer y Muller demostraron que los átomos de Xe sujetos a pulsos láser cortos podían sobrevivir en los estados altamente excitados 4f, 5f y 6f. Se creía que estos estados habían sido excitados por el cambio dinámico de Stark de los niveles en resonancia multifotónica con el campo durante la parte ascendente del pulso láser. La evolución posterior del pulso láser no ionizó por completo estos estados, dejando atrás algunos átomos altamente excitados. Nos referiremos a este fenómeno como "trampa de población".

Presentación esquemática de la población de tipo lambda. G es el estado del átomo. 1 y 2 son dos estados excitados degenerados. Después de que la población se transfiere a los estados debido a la resonancia multifotón, estos estados se unen a través del continuo c y la población está atrapada en la superposición de estos estados.

Mencionamos el cálculo teórico de que se produce una ionización incompleta siempre que haya una excitación resonante paralela en un nivel común con pérdida de ionización. Consideramos un estado como 6f de Xe que consta de 7 niveles cuasi-degenerados en el rango del ancho de banda del láser. Estos niveles junto con el continuo constituyen un sistema lambda. El mecanismo del atrapamiento de tipo lambda se presenta esquemáticamente en la figura. En la parte ascendente del pulso (a), el estado excitado (con dos niveles degenerados 1 y 2) no está en resonancia multifotónica con el estado fundamental. El electrón se ioniza a través del acoplamiento multifotónico con el continuo. A medida que aumenta la intensidad del pulso, el estado excitado y el continuo cambian de energía debido al cambio de Stark. En el pico del pulso (b), los estados excitados entran en resonancia multifotónica con el estado fundamental. A medida que la intensidad comienza a disminuir (c), los dos estados se acoplan a través de un continuo y la población queda atrapada en una superposición coherente de los dos estados. Bajo la acción posterior del mismo pulso, debido a la interferencia en las amplitudes de transición del sistema lambda, el campo no puede ionizar completamente a la población y una fracción de la población quedará atrapada en una superposición coherente de los niveles casi degenerados. Según esta explicación los estados con mayor momento angular -con más subniveles- tendrían mayor probabilidad de atrapar a la población. En general, la fuerza de la captura estará determinada por la fuerza del acoplamiento de dos fotones entre los niveles cuasi-degenerados a través del continuo. En 1996, utilizando el láser muy estable y minimizando los efectos de enmascaramiento de la expansión de la región focal con intensidad creciente, Talebpour et al. estructuras observadas en las curvas de iones cargados individualmente de Xe, Kr y Ar. Estas estructuras se atribuyeron a la captura de electrones en el campo láser fuerte. T. Morishita y C. D. Lin han informado de una demostración más inequívoca de captura de población.

Ionización múltiple no secuencial

El fenómeno de la ionización no secuencial (NSI) de los átomos expuestos a campos láser intensos ha sido objeto de muchos estudios teóricos y experimentales desde 1983. El trabajo pionero comenzó con la observación de una estructura "knee" en el Xe²⁺ curva de señal de iones versus intensidad de L’Huillier et al. Desde el punto de vista experimental, la doble ionización del NS se refiere a procesos que de alguna manera aumentan la tasa de producción de iones doblemente cargados por un enorme factor a intensidades por debajo de la intensidad de saturación del ion cargado. Muchos, por otro lado, prefieren definir la NSI como un proceso por el cual dos electrones se ionizan casi simultáneamente. Esta definición implica que aparte del canal secuencial ${displaystyle A+L- titulada A^{+}+L- titulada A^{++}$ hay otro canal ${displaystyle A+L- titulada A^{++}$ que es la principal contribución a la producción de iones doblemente cargados a menores intensidades. La primera observación de triple NSI en argón interactuando con un láser de 1 μm fue reportada por Augst et al. Más tarde, estudiando sistemáticamente la NSI de todos los átomos de gas raros, se observó la INS cuádruple de Xe. La conclusión más importante de este estudio fue la observación de la siguiente relación entre la tasa de NSI a cualquier estado de carga y la tasa de ionización del túnel (predictada por la fórmula ADK) a los estados de carga anteriores;

${displaystyle W_{NS}(A^{n+})=sum ¿Por qué?$

Donde ${displaystyle W_{ADK}left(A^{i+}right)}$ es la tasa de túnel cuasi estático a cargo del estado y ${displaystyle alpha _{n}(lambda)}$ son algunas constantes dependiendo de la longitud de onda del láser (pero no en la duración del pulso).

Se han propuesto dos modelos para explicar la ionización no secuencial; el modelo de sacudida y el modelo de redispersión de electrones. El modelo de sacudida (SO), propuesto por primera vez por Fittinghoff et al., se adopta del campo de la ionización de átomos por rayos X y proyectiles de electrones donde el proceso SO es uno de los principales mecanismos responsables de la ionización múltiple de átomos. El modelo SO describe el proceso NS como un mecanismo en el que el campo láser ioniza un electrón y la salida de este electrón es tan rápida que los electrones restantes no tienen tiempo suficiente para adaptarse a los nuevos estados de energía. Por tanto, existe cierta probabilidad de que, tras la ionización del primer electrón, un segundo electrón sea excitado a estados de mayor energía (shake-up) o incluso ionizado (shake-off). Cabe mencionar que, hasta el momento, no se ha realizado un cálculo cuantitativo basado en el modelo SO, y el modelo sigue siendo cualitativo.

El modelo de recattering de electrones fue desarrollado independientemente por Kuchiev, Schafer et, Corkum, Becker y Faisal y Faisal y Becker. Las características principales del modelo se pueden entender fácilmente desde la versión de Corkum. El modelo de Corkum describe la ionización del NS como un proceso por el cual un electrón es ionizado túnel. El electrón entonces interactúa con el campo láser donde se acelera lejos del núcleo nuclear. Si el electrón ha sido ionizado en una fase apropiada del campo, pasará por la posición del ion restante medio ciclo más tarde, donde puede liberar un electron adicional por impacto de electrones. Sólo la mitad del tiempo el electrón se libera con la fase apropiada y la otra mitad nunca vuelve al núcleo nuclear. La energía cinética máxima que puede tener el electrón retornante es 3.17 veces el potencial ponderomotivo (${displaystyle U_{p}$El láser. El modelo de Corkum coloca un límite de corte en la intensidad mínima (${displaystyle U_{p}$ es proporcional a la intensidad) donde puede ocurrir ionización debido a la reescattering.

Diagrama Feynman para el proceso de ionización doble en un átomo a través del mecanismo de re-escattering

El modelo de redispersión en la versión de Kuchiev (modelo de Kuchiev) es mecánico cuántico. La idea básica del modelo se ilustra mediante diagramas de Feynman en la figura a. Primero, ambos electrones están en el estado fundamental de un átomo. Las líneas marcadas con a y b describen los estados atómicos correspondientes. Entonces el electrón a se ioniza. El comienzo del proceso de ionización se muestra mediante la intersección con una línea discontinua inclinada. donde ocurre el MPI. La línea gruesa completa muestra la propagación del electrón ionizado en el campo láser, durante el cual absorbe otros fotones (ATI). La colisión de este electrón con el ion atómico principal se muestra mediante una línea punteada vertical que representa la interacción de Coulomb entre los electrones. El estado marcado con c describe la excitación de iones a un estado discreto o continuo. La figura b describe el proceso de intercambio. El modelo de Kuchiev, al contrario que el modelo de Corkum, no predice ningún umbral de intensidad para la aparición de ionización NS.

Kuciev no incluyó los efectos de Coulomb en la dinámica del electrón ionizado. Esto resultó en la subestimación de la tasa de doble ionización por un factor enorme. Obviamente, en el enfoque de Becker y Faisal (que es equivalente en espíritu al modelo de Kuchiev), este inconveniente no existe. De hecho, su modelo es más exacto y no sufre la gran cantidad de aproximaciones realizadas por Kuchiev. Los resultados de sus cálculos encajan perfectamente con los resultados experimentales de Walker et al. Becker y Faisal han podido ajustar los resultados experimentales en el NSI múltiple de átomos de gases raros utilizando su modelo. Como resultado, la redispersión de electrones puede tomarse como el mecanismo principal para que ocurra el proceso NSI.

Ionización multifotónica de electrones de valencia interna y fragmentación de moléculas poliatómicas

La ionización de los electrones de valencia internos es responsable de la fragmentación de moléculas poliatómicas en campos láser intensos. Según un modelo cualitativo, la disociación de las moléculas se produce a través de un mecanismo de tres pasos:

• MPI de electrones de las órbitas internas de la molécula que resulta en un ión molecular en niveles ro-vibracionales de un estado electrónico excitado;
• Transición rápida sin radiación a los altos niveles de rotación de un estado electrónico inferior; y
• Disociación posterior del ión a diferentes fragmentos a través de diversos canales de fragmentación.

La fragmentación molecular inducida por pulsos cortos se puede utilizar como fuente de iones para la espectroscopia de masas de alto rendimiento. La selectividad proporcionada por una fuente basada en pulsos cortos es superior a la esperada cuando se utilizan fuentes convencionales basadas en ionización de electrones, en particular cuando se requiere la identificación de isómeros ópticos.

Encuadre de Kramers-Henneberger y efectos de fase de ionización

El estudio de la ionización de campo fuerte del átomo en el llamado marco de Kramers-Henneberger (K-H) lleva a la conclusión de que la eficiencia de ionización depende en gran medida de los detalles temporales del pulso ionizante, pero no necesariamente de la intensidad del campo y la energía total. del pulso ionizante bombeado en el átomo. El marco de Kramers-Henneberger es el marco no intercial que se mueve con el electrón libre bajo la influencia del pulso láser armónico. La solución de electrones libres de las ecuaciones de Newton para el electrón en una dimensión en el campo láser armónico

${displaystyle {frac {mathrm} {2}x}{mathrm {d} t^{2}}}=Fsin(omega t)}$

será también armónico

${displaystyle x(t)=-{frac}{omega ^{2}sin(omega t)=-asin(omega t)}$

El marco que comova con este electrón se obtendrá mediante la transformación de coordenadas

${displaystyle xto x+asin(omega t)}$

mientras que el potencial de Coulomb añadido será

${displaystyle V(x)=-{frac {1}{left hyperx+asin(omega t)right WordPress}}}$

El promedio de tiempo de ciclo completo de ese potencial que es

${displaystyle ¿Qué?$

será la función de ${displaystyle x}$ y por lo tanto tener el máximo ${displaystyle x=0}$ mientras que para esa condición inicial la solución será ${displaystyle x(t)=0}$ en el K-H y por lo tanto será idéntico a la solución de electrones libres en el marco de laboratorio. La velocidad de electrones en la otra mano se desplaza tanto a la fuerza de campo como a la posición de electrones:

${displaystyle {frac {mathrm {d}{mathrm {d}} {m}} {m}} {m} {cH0}}}} {cH0}}}}}} {m}}}}} {m} {fnK}}cos(omega t)}$

Por lo tanto, considerando los pulsos de onda y definiendo la ionización como el escape completo del segmento de línea de la longitud 2r (o de la región esférica en tres dimensiones) la ionización completa ocurre en el modelo clásico después del tiempo ${displaystyle r/(aomega)}$ o ninguna ionización dependiendo de si la onda de campo armónico se corta al mínimo cero o la velocidad máxima.

Disociación – distinción

Una sustancia puede disociarse sin producir necesariamente iones. Como ejemplo, las moléculas de azúcar de mesa se disocian en agua (el azúcar se disuelve) pero existen como entidades neutras intactas. Otro evento sutil es la disociación del cloruro de sodio (sal de mesa) en iones de sodio y cloro. Aunque pueda parecer un caso de ionización, en realidad los iones ya existen dentro de la red cristalina. Cuando la sal se disocia, sus iones constituyentes simplemente están rodeados por moléculas de agua y sus efectos son visibles (por ejemplo, la solución se vuelve electrolítica). Sin embargo, no se produce transferencia o desplazamiento de electrones.

Mesa