Intervalo de confianza

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Rango para estimar un parámetro desconocido

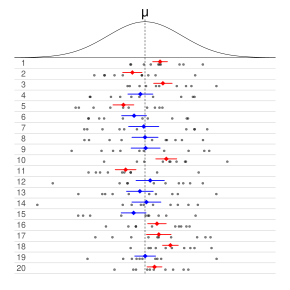
En estadísticas frecuentistas, un intervalo de confianza (IC) es un rango de estimaciones para un parámetro desconocido. Se calcula un intervalo de confianza en un nivel de confianza designado; el nivel de confianza del 95 % es el más común, pero a veces se utilizan otros niveles, como el 90 % o el 99 %. El nivel de confianza, grado de confianza o coeficiente de confianza representa la proporción a largo plazo de IC (en el nivel de confianza dado) que teóricamente contienen el verdadero valor del parámetro; esto equivale a la probabilidad de cobertura nominal. Por ejemplo, de todos los intervalos calculados al nivel del 95 %, el 95 % de ellos debe contener el valor real del parámetro.

Los factores que afectan el ancho del IC incluyen el tamaño de la muestra, la variabilidad de la muestra y el nivel de confianza. Si todo lo demás es igual, una muestra más grande produce un intervalo de confianza más estrecho, una mayor variabilidad en la muestra produce un intervalo de confianza más amplio y un nivel de confianza más alto produce un intervalo de confianza más amplio.

Definición

Vamos $X$ ser una muestra aleatoria de una distribución de probabilidad con parámetro estadístico $theta$ , que es una cantidad a estimar, y $varphi$ , representando cantidades que no son de interés inmediato. Un intervalo de confianza para el parámetro $theta$ , con nivel de confianza o coeficiente $gamma$ , es un intervalo ${displaystyle (u(X),v(X))}$ determinado por variables aleatorias $u(X)$ y ${displaystyle v(X)}$ con la propiedad:

<math alttext="{displaystyle P(u(X)<theta P()u()X).Silencio Silencio .v()X))=γ γ para todos()Silencio Silencio ,φ φ ).{displaystyle P(u(X) interpretadotheta יv(X))=gamma quad {text{ for every } {thetavarphi).} <img alt="{displaystyle P(u(X)<theta

El número $gamma$ , cuyo valor típico es cercano pero no mayor de 1, a veces se da en la forma $1-alpha$ (o como porcentaje) ${displaystyle 100%cdot (1-alpha)}$ ), donde $alpha$ es un pequeño número positivo, a menudo 0,05.

Es importante para los límites $u(X)$ y ${displaystyle v(X)}$ que se especifique de tal manera que $X$ se recoge aleatoriamente, cada vez que computamos un intervalo de confianza, hay probabilidad $gamma$ que contendría $theta$ , se estima el verdadero valor del parámetro. Esto debe ser cierto para cualquier realidad $theta$ y $varphi$ .

Intervalos de confianza aproximados

En muchas aplicaciones, los intervalos de confianza que tienen exactamente el nivel de confianza requerido son difíciles de construir, pero se pueden calcular intervalos aproximados. La regla para construir el intervalo puede ser aceptada como proporcionar un intervalo de confianza a nivel $gamma$ si

<math alttext="{displaystyle P(u(X)<theta P()u()X).Silencio Silencio .v()X)).. γ γ para todos()Silencio Silencio ,φ φ ){displaystyle P(u(X) madetheta יv(X))approx gamma quad {text{ for every } {thetavarphi)} <img alt="{displaystyle P(u(X)<theta

a un nivel aceptable de aproximación. Alternativamente, algunos autores simplemente requieren que

<math alttext="{displaystyle P(u(X)<theta P()u()X).Silencio Silencio .v()X))\geq \geq γ γ para todos()Silencio Silencio ,φ φ ),{displaystyle P(u(X) seleccionótheta <v(X))geq gamma quad {text{ for every } {thetavarphi),} <img alt="{displaystyle P(u(X)<theta

lo cual es útil si las probabilidades están solo parcialmente identificadas o son imprecisas, y también cuando se trata de distribuciones discretas. Límites de confianza de la forma

<math alttext="{displaystyle P(u(X)P()u()X).Silencio Silencio )\geq \geq γ γ {displaystyle P(u(X) madetheta)geq gamma } <img alt="{displaystyle P(u(X)

<math alttext="{displaystyle P(theta P()Silencio Silencio .v()X))\geq \geq γ γ {displaystyle P(theta v(X))geq gamma } <img alt="{displaystyle P(theta

son llamados conservadores; en consecuencia, se habla de intervalos de confianza conservadores y, en general, de regiones.

Propiedades deseadas

Al aplicar procedimientos estadísticos estándar, a menudo habrá formas estándar de construir intervalos de confianza. Estos habrán sido diseñados para cumplir con ciertas propiedades deseables, que se mantendrán dado que los supuestos en los que se basa el procedimiento son ciertos. Estas propiedades deseables pueden describirse como: validez, optimización e invariancia.

De los tres, "validez" es el más importante, seguido de cerca por la "optimidad". "Invarianza" puede considerarse como una propiedad del método de derivación de un intervalo de confianza, más que de la regla para construir el intervalo. En aplicaciones no estándar, se buscarían estas mismas propiedades deseables:

Validez

Esto significa que la probabilidad de cobertura nominal (nivel de confianza) del intervalo de confianza debe mantenerse, ya sea exactamente o con una buena aproximación.

Optimidad

Esto significa que la regla para construir el intervalo de confianza debe hacer el mayor uso posible de la información del conjunto de datos.

Recuerde que uno podría descartar la mitad de un conjunto de datos y aún así obtener un intervalo de confianza válido. Una forma de evaluar la optimización es por la longitud del intervalo, de modo que una regla para construir un intervalo de confianza se considere mejor que otra si conduce a intervalos cuyas longitudes suelen ser más cortas.

Invariancia

En muchas aplicaciones, es posible que la cantidad que se estima no esté bien definida como tal.

Por ejemplo, una encuesta puede dar como resultado una estimación de la mediana de ingresos en una población, pero también podría considerarse que proporciona una estimación del logaritmo de la mediana de ingresos, dado que se trata de una escala común para presentar resultados gráficos.. Sería deseable que el método utilizado para construir un intervalo de confianza para la renta mediana diera resultados equivalentes cuando se aplica a construir un intervalo de confianza para el logaritmo de la renta mediana: Específicamente los valores en los extremos de este último intervalo serían los logaritmos de los valores en los extremos del intervalo anterior.

Métodos de derivación

Para aplicaciones no estándar, hay varias rutas que se pueden tomar para derivar una regla para la construcción de intervalos de confianza. Las reglas establecidas para los procedimientos estándar pueden justificarse o explicarse a través de varias de estas vías. Por lo general, una regla para construir intervalos de confianza está estrechamente ligada a una forma particular de encontrar una estimación puntual de la cantidad que se está considerando.

Resumen de estadísticas

Esto está estrechamente relacionado con el método de los momentos para la estimación. Surge un ejemplo simple donde la cantidad a estimar es la media de la población, en cuyo caso una estimación natural es la media de la muestra. De manera similar, la varianza de la muestra se puede usar para estimar la varianza de la población. Se puede construir un intervalo de confianza para la media real centrado en la media de la muestra con un ancho que sea un múltiplo de la raíz cuadrada de la varianza de la muestra.

Teoría de la probabilidad

Las estimaciones se pueden construir usando el principio de máxima verosimilitud, la teoría de probabilidad para esto proporciona dos formas de construir intervalos de confianza o regiones de confianza para las estimaciones.

Estimación de ecuaciones

El enfoque de estimación aquí puede considerarse como una generalización del método de momentos y una generalización del enfoque de máxima verosimilitud. Hay generalizaciones correspondientes de los resultados de la teoría de máxima verosimilitud que permiten construir intervalos de confianza basados en estimaciones derivadas de la estimación de ecuaciones.

Prueba de hipótesis

Si las pruebas de hipótesis están disponibles para los valores generales de un parámetro, entonces se pueden construir regiones/intervalos de confianza incluyendo en el 100 $p$ % región de confianza todos aquellos puntos para los cuales la prueba de hipótesis de la hipótesis nula de que el valor verdadero es el valor dado no se rechaza a un nivel de significación de (1 − $p$ ).

Bootstrapping

En situaciones en las que los supuestos de distribución de los métodos anteriores son inciertos o se violan, los métodos de remuestreo permiten la construcción de intervalos de confianza o intervalos de predicción. La distribución de datos observados y las correlaciones internas se utilizan como sustitutos de las correlaciones en la población más amplia.

Teorema del límite central

El teorema límite central es un refinamiento de la ley de grandes números. Para un gran número de variables independientes distribuidas al azar ${displaystyle X_{1},...,X_{n},}$ con varianza finita, el promedio ${overline {X}}_{n}$ aproximadamente tiene una distribución normal, sin importar la distribución de la $X_{i}$ es, con la aproximación mejorar en proporción a ${sqrt {n}}$ .

Ejemplo

En este gráfico de barras, los extremos superiores de las barras marrones indican los medios observados y los segmentos de la línea roja ("rejas de terror") representan los intervalos de confianza alrededor de ellos. Aunque las barras de error se muestran como simétricas alrededor de los medios, eso no es siempre el caso. En la mayoría de los gráficos, las barras de errores no representan intervalos de confianza (por ejemplo, a menudo representan errores estándar o desviaciones estándar).

Suppose ${displaystyle {X_{1},ldotsX_{n}}}$ es una muestra independiente de una población normalmente distribuida con parámetros desconocidos $mu$ y diferencia ${displaystyle sigma ^{2}.}$ Vamos

{displaystyle {bar {X}}={frac {X_{1}+cdots +X_{n}}{n}},}

{displaystyle S^{2}={frac {1}{n-1}}sum _{i=1}^{n}(X_{i}-{bar {X}})^{2}.}

Donde ${bar {X}}$ es la muestra media, y $S^{2}$ es la variación de la muestra. Entonces...

{displaystyle T={frac {{bar {X}}-mu }{S/{sqrt {n}}}}}

tiene una distribución t Estudiante con $n-1$ grados de libertad. Note que la distribución de $T$ no depende de los valores de los parámetros inservibles $mu$ y $sigma ^{2}$ ; es decir, es una cantidad pivotal. Supongamos que queríamos calcular un intervalo de confianza del 95% $mu.$ Entonces, denotando $c$ como el percentil 97.5 de esta distribución,

{displaystyle P(-cleq Tleq c)=0.95.}

Tenga en cuenta que "97.5" y "0.95" son correctos en las expresiones anteriores. Hay un 2,5% de probabilidades de que $T$ será menos que $-c$ y un 2,5% de probabilidad de que sea más grande que ${displaystyle +c.}$ Así, la probabilidad de que $T$ será entre $-c$ y ${displaystyle +c}$ es el 95%.

En consecuencia,

{displaystyle Pleft({bar {X}}-{frac {cS}{sqrt {n}}}leq mu leq {bar {X}}+{frac {cS}{sqrt {n}}}right)=0.95,}

y tenemos un intervalo teórico de confianza del 95% para $mu.$

Después de observar la muestra encontramos valores ${bar {x}}$ para ${bar {X}}$ y $s$ para $S,$ desde el cual calculamos el intervalo de confianza

{displaystyle left[{bar {x}}-{frac {cs}{sqrt {n}}},{bar {x}}+{frac {cs}{sqrt {n}}}right].}

Interpretación

Se pueden dar varias interpretaciones de un intervalo de confianza (tomando el intervalo de confianza del 95 % como ejemplo a continuación).

El intervalo de confianza se puede expresar en términos de una frecuencia de larga duración en muestras repetidas (o en el muestreo): "Si este procedimiento se repite en numerosas muestras, la proporción de intervalos calculados de confianza del 95% que abarcan el verdadero valor del parámetro de población tendería hacia el 95%".
El intervalo de confianza se puede expresar en términos de probabilidad con respecto a una única muestra teórica (sin darse cuenta): "Hay una probabilidad del 95% de que el intervalo de confianza del 95% calculado a partir de una muestra futura cubrirá el verdadero valor del parámetro de población". Esto esencialmente replantea la interpretación de las "muestras repetidas" como una probabilidad en lugar de una frecuencia.
El intervalo de confianza se puede expresar en términos de significación estadística, por ejemplo: "El intervalo de confianza del 95% representa valores que no son estadísticamente significativamente diferentes de la estimación de puntos en el nivel.05."

Errores comunes

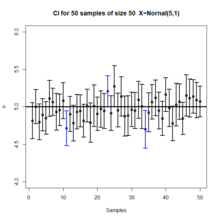
Los niveles y los intervalos de confianza se malinterpretan con frecuencia, y los estudios publicados han demostrado que incluso los científicos profesionales a menudo los malinterpretan.

Un nivel de confianza del 95% no significa que para un intervalo determinado haya una probabilidad del 95% de que el parámetro de población se encuentra dentro del intervalo (es decir, una probabilidad del 95% que cubre el parámetro de población). Según la estricta interpretación frecuenteista, una vez que se calcula un intervalo, este intervalo cubre el valor del parámetro o no; ya no es cuestión de probabilidad. La probabilidad del 95% se refiere a la fiabilidad del procedimiento de estimación, no a un intervalo calculado específico. El propio Neyman (el proponente original de intervalos de confianza) hizo este punto en su documento original:
Se notará que en la descripción anterior, las declaraciones de probabilidad se refieren a los problemas de estimación con los que el estadístico se ocupará en el futuro. De hecho, he declarado repetidamente que la frecuencia de los resultados correctos tenderá a α. Considere ahora el caso cuando una muestra ya se dibuja, y los cálculos han dado [límites parciales]. Podemos decir que en este caso particular la probabilidad del verdadero valor [cayendo entre estos límites] es igual a α? La respuesta es obviamente negativa. El parámetro es una constante desconocida, y no se puede hacer ninguna declaración de probabilidad sobre su valor...

Deborah Mayo se expande más de la siguiente manera:

Debe subrayarse, sin embargo, que habiendo visto el valor [de los datos], la teoría Neyman-Pearson nunca permite concluir que el intervalo de confianza específico formado cubre el verdadero valor de 0 con uno o uno (1 −α)100% probabilidad o (1 −α100% de confianza. La observación de Seidenfeld parece arraigada en un deseo (no poco común) de intervalos de confianza de Neyman-Pearson para proporcionar algo que no pueden proporcionar legítimamente; es decir, una medida del grado de probabilidad, creencia o apoyo que un valor de parámetro desconocido está en un intervalo específico. Después de Savage (1962), la probabilidad de que un parámetro se encuentre en un intervalo específico puede denominarse una medida de precisión final. Aunque una medida de precisión final puede parecer deseable, y aunque los niveles de confianza a menudo se interpretan (por error) como una medida de ese tipo, no se justifica tal interpretación. Es cierto que tal interpretación errónea es estimulada por la palabra "confianza".

Un nivel de confianza del 95% no significa que el 95% de los datos de la muestra se encuentran dentro del intervalo de confianza.
Un intervalo de confianza no es una gama definitiva de valores plausibles para el parámetro de muestra, aunque a menudo se toma heurísticamente como una gama de valores plausibles.
Un nivel de confianza particular del 95% calculado a partir de un experimento no significa que haya una probabilidad del 95% de un parámetro de muestra a partir de una repetición del experimento que cae dentro de este intervalo.

Contraejemplos

Desde que se propuso la teoría del intervalo de confianza, se han desarrollado una serie de contraejemplos de la teoría para mostrar cómo la interpretación de los intervalos de confianza puede ser problemática, al menos si uno los interpreta de manera ingenua.

Procedimiento de confianza para ubicación uniforme

Welch presentó un ejemplo que muestra claramente la diferencia entre la teoría de los intervalos de confianza y otras teorías de estimación de intervalos (incluidos los intervalos fiduciales de Fisher y los intervalos bayesianos objetivos). Robinson llamó a este ejemplo '[posiblemente] el contraejemplo más conocido de la versión de la teoría del intervalo de confianza de Neyman'. Para Welch, mostró la superioridad de la teoría del intervalo de confianza; para los críticos de la teoría, muestra una deficiencia. Aquí presentamos una versión simplificada.

Supongamos que $X_{1},X_{2}$ son observaciones independientes de un uniforme ${displaystyle (theta -1/2,theta +1/2)}$ distribución. Luego el procedimiento de confianza óptimo del 50% $theta$ es

<math alttext="{displaystyle {bar {X}}pm {begin{cases}{dfrac {|X_{1}-X_{2}|}{2}}&{text{if }}|X_{1}-X_{2}|X̄ ̄ ± ± {}SilencioX1− − X2Silencio2siSilencioX1− − X2Silencio.1/21− − SilencioX1− − X2Silencio2siSilencioX1− − X2Silencio≥ ≥ 1/2.{displaystyle {bar {X}pm {begin{cases}{dfrac {x_{1}-X_{2} - ¿Qué? {2} {2}} {2} {f}} {f}}} {f}} } minucioso.<img alt="{displaystyle {bar {X}}pm {begin{cases}{dfrac {|X_{1}-X_{2}|}{2}}&{text{if }}|X_{1}-X_{2}|

Se puede utilizar un argumento bayesiano fiduciario u objetivo para derivar la estimación del intervalo

{displaystyle {bar {X}}pm {frac {1-|X_{1}-X_{2}|}{4}},}

que es también un procedimiento de confianza del 50%. Welch mostró que el primer procedimiento de confianza domina el segundo, según desiderata de la teoría del intervalo de confianza; para cada ${displaystyle theta _{1}neq theta }$ , la probabilidad de que el primer procedimiento contenga $theta _{1}$ es menos que o igual a la probabilidad de que el segundo procedimiento contenga $theta _{1}$ . El ancho promedio de los intervalos del primer procedimiento es inferior al del segundo. Por lo tanto, el primer procedimiento es preferido bajo la teoría del intervalo de confianza clásico.

Sin embargo, cuando ${displaystyle |X_{1}-X_{2}|geq 1/2}$ , intervalos del primer procedimiento son garantizado para contener el valor verdadero $theta$ : Por lo tanto, el coeficiente nominal de confianza del 50% no está relacionado con la incertidumbre que debemos tener que un intervalo específico contiene el valor verdadero. El segundo procedimiento no tiene esta propiedad.

Además, cuando el primer procedimiento genera un intervalo muy corto, esto indica que $X_{1},X_{2}$ son muy unidos y por lo tanto sólo ofrecen la información en un solo punto de datos. Sin embargo, el primer intervalo excluirá casi todos los valores razonables del parámetro debido a su ancho corto. El segundo procedimiento no tiene esta propiedad.

Las dos propiedades contra-intuitivas del primer procedimiento – 100% de cobertura cuando $X_{1},X_{2}$ son muy separados y casi 0% cobertura cuando $X_{1},X_{2}$ están unidos – balance de rendimiento del 50% de cobertura en promedio. Sin embargo, a pesar de que el primer procedimiento es óptimo, sus intervalos no ofrecen una evaluación de la precisión de la estimación ni una evaluación de la incertidumbre que uno debe tener que el intervalo contiene el valor verdadero.

Este contraejemplo se utiliza para argumentar en contra de las interpretaciones ingenuas de los intervalos de confianza. Si se afirma que un procedimiento de confianza tiene propiedades más allá de la cobertura nominal (como la relación con la precisión o una relación con la inferencia bayesiana), esas propiedades deben probarse; no se derivan del hecho de que un procedimiento sea un procedimiento de confianza.

Procedimiento de confianza para ω2

Steiger sugirió una serie de procedimientos de confianza para medidas comunes de tamaño de efecto en ANOVA. Morey et al. señalan que varios de estos procedimientos de confianza, incluido el ⋅², tener la propiedad que como F la estadística se vuelve cada vez más pequeña: indicar el mal ajuste con todos los valores posibles ⋅²—el intervalo de confianza se encoge e incluso puede contener sólo el valor único ⋅²= 0; es decir, el CI es infinitamente estrecho (esto ocurre cuando ${displaystyle pgeq 1-alpha /2}$ para un $100(1-alpha)%$ CI).

Este comportamiento es coherente con la relación entre el procedimiento de confianza y la prueba de significación: a medida que F se vuelve tan pequeño que las medias del grupo están mucho más juntas de lo que esperaríamos por casualidad, una prueba de significancia podría indicar rechazo para la mayoría o todos los valores de ω². Por lo tanto, el intervalo será muy estrecho o incluso vacío (o, según una convención sugerida por Steiger, contendrá solo 0). Sin embargo, esto no indica que la estimación de ω² sea muy precisa. En cierto sentido, indica lo contrario: que la confiabilidad de los resultados mismos puede estar en duda. Esto es contrario a la interpretación común de los intervalos de confianza que revelan la precisión de la estimación.

Historia

Los métodos para calcular los intervalos de confianza para la proporción binomial aparecieron a partir de la década de 1920. Las ideas principales de los intervalos de confianza en general se desarrollaron a principios de la década de 1930, y Jerzy Neyman dio la primera descripción completa y general en 1937.

Neyman describió el desarrollo de las ideas de la siguiente manera (se cambiaron los números de referencia):

[Mi trabajo sobre intervalos de confianza] originó alrededor de 1930 de una simple cuestión de Waclaw Pytkowski, luego mi estudiante en Varsovia, dedicado a un estudio empírico en economía agrícola. La pregunta fue: ¿cómo caracterizar no-dogmáticamente la precisión de un coeficiente de regresión estimado?...
La monografía de Pytkowski apareció en 1932. Sucedió que, algo antes, Fisher publicó su primer documento relacionado con distribuciones fiduciales y argumentos fiduciales. Inesperadamente, mientras que el marco conceptual del argumento fiducial es totalmente diferente al de los intervalos de confianza, coincidieron las soluciones específicas de varios problemas particulares. Así, en el primer artículo en el que presenté la teoría de intervalos de confianza, publicada en 1934, reconocí la prioridad de Fisher para la idea de que la estimación de intervalos es posible sin ninguna referencia al teorema de Bayes y con la solución siendo independiente de probabilidades a priori. Al mismo tiempo, levemente sugerí que el enfoque de Fisher para el problema implicaba un malentendido menor.

En las revistas médicas, los intervalos de confianza se promovieron en la década de 1970, pero solo se generalizaron en la década de 1980. En 1988, las revistas médicas exigían la notificación de intervalos de confianza.

Contenido relacionado

Más resultados...