Interpolación cúbica monótona

En el campo matemático del análisis numérico, la interpolación cúbica monótona es una variante de la interpolación cúbica que preserva la monotonía del conjunto de datos que se interpola.

La monotonía se conserva mediante la interpolación lineal, pero no se garantiza mediante la interpolación cúbica.

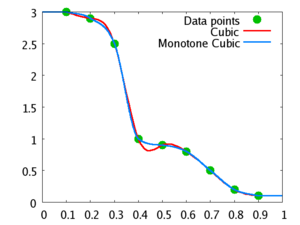
La interpolación de monotona se puede lograr utilizando la línea hermita cúbica con los tangentes ${\displaystyle m_{i}$ modificado para asegurar la monotónica de la línea Hermite resultante.

También está disponible un algoritmo para la interpolación monótona de Hermite de quinto grado.

Existen varias formas de seleccionar tangentes de interpolación para cada punto de datos. En esta sección se describirá el uso del método Fritsch-Carlson. Tenga en cuenta que solo se requiere una pasada del algoritmo.

Que los puntos de datos sean ${\displaystyle (x_{k},y_{k}}$ indexado en orden clasificado ${\displaystyle k=1,\,\dots \,n}$.

1. Computar las pistas de las líneas de secant entre puntos sucesivos:

   ${\displaystyle \delta ¿Qué? {y_{k+1}-y_{k} {x_{k+1}-x_{k}}}$

   para ${\displaystyle k=1,\,\dots \,n-1}$.
   
   
2. Estas asignaciones son provisionales y pueden ser superadas en los pasos restantes. Iniciar los tangentes en cada punto de datos interior como el promedio de los secantes,

   ${\displaystyle m_{k}={\frac {\delta _{k-1}+\delta ¿Qué?$

   para ${\displaystyle k=2,\,\dots \,n-1}$.
   
   Para los puntos finales, utilice diferencias unilaterales:

   ${\displaystyle m_{1}=\delta ¿Por qué? m_{n}=\delta - ¿Qué?$.

   Si ${\displaystyle \delta ¿Qué?$ y ${\displaystyle \delta _{k}$ tienen signos opuestos, conjunto ${\displaystyle m_{k}=0}$.
   
   
3. Para ${\displaystyle k=1,\,\dots \,n-1}$, donde siempre ${\displaystyle \delta _{k}=0}$ (dondequiera dos sucesos ${\displaystyle Y...$ son iguales),
   set ${\displaystyle m_{k}=m_{k+1}=0,}$ como la línea que conecta estos puntos debe ser plana para preservar la monotónica.
   Ignorar los pasos 4 y 5 para aquellos ${\displaystyle k\,}$.
   
   
4. Vamos.

   ${\displaystyle \alpha ¿Qué? - ¿Por qué? ### {k}=m_{k+1}/\delta ¿Qué?$.

   Si ${\displaystyle \alpha _{k}$ o ${\displaystyle \beta _{k}$ es negativo, entonces los puntos de datos de entrada no son estrictamente monotone, y ${\displaystyle (x_{k},\,y_{k}}$ es un extremum local. En esos casos, en sentido parcial curvas monotone todavía se puede generar eligiendo ${\displaystyle m_{k}=0\,}$ si ${\displaystyle \alpha _{k}traducido0}$ o ${\displaystyle m_{k+1}=0\,}$ si ${\displaystyle \beta _{k}traducido0}$, aunque la monotónica estricta no es posible a nivel mundial.
   
   
5. Para evitar el sobresueldo y asegurar la monotónica, se debe cumplir al menos una de las tres condiciones siguientes:

a) la función

${\displaystyle \phi _{k}=\alpha ¿Por qué? ¿Qué?$, o

b) ${\displaystyle \alpha _{k}+2\beta _{k}-3\leq 0\,}$, o

c) ${\displaystyle 2\alpha _{k}+\beta _{k}-3\leq 0\,}$.

Sólo la condición a) es suficiente para garantizar la monotónica estricta: ${\displaystyle \phi _{k}$ Debe ser positivo.

Una manera sencilla de satisfacer esta limitación es restringir el vector ${\displaystyle (\alpha _{k},\beta _{k})}$ a un círculo de radio 3. ${\displaystyle \alpha ¿Qué? ¿Qué?$, entonces listo

${\displaystyle \tau _{k}={\frac {3}{\sqrt {\alpha ¿Qué? .$,

y reescala los tangentes a través

${\displaystyle ################# {k}\,\delta _{k}\quad {\text{ and }\quad m_{k+1}=\tau _{k}\,\beta ¿Por qué? ¿Qué?$.

Alternativamente es suficiente restringir ${\displaystyle \alpha _{k}\leq 3}$ y ${\displaystyle \beta _{k}\leq 3\,}$. Para lograr esto, si ${\displaystyle \alpha _{k} título3\,}$, entonces listo ${\displaystyle m_{k}=3\,\delta ¿Qué?$Y si ${\displaystyle \beta _{k} título3\,}$, entonces listo ${\displaystyle m_{k+1}=3\,\delta ¿Qué?$.

Después del preprocesamiento anterior, la evaluación de la línea interpolada es equivalente a la línea cúbica Hermite, utilizando los datos ${\displaystyle x_{k}$, ${\displaystyle y_{k}$, y ${\displaystyle m_{k}$ para ${\displaystyle k=1,\,\dots \,n}$.

Para evaluar ${\displaystyle x}$, encontrar el índice ${\displaystyle k}$ en la secuencia donde ${\displaystyle x}$, mentiras entre ${\displaystyle x_{k}$, y ${\displaystyle x_{k+1}}$, es decir: ${\displaystyle x_{k}\leq x\leq x_{k+1}$. Cálculo

${\displaystyle \Delta =x_{k+1}-x_{k}\quad {\text{ and }\quad t={\frac {x-x_{k}{\ Delta }$

entonces el valor interpolado es

${\displaystyle f_{\text{interpolated}(x)=y_{k}\cdot h_{00}(t)+\Delta \cdot m_{k}\cdot h_{10}(t)+y_{k+1}\cdot h_{01}(t)+\ Delta \cdot m_{k+1}\cdot h_{11}(t)}$

Donde ${\displaystyle H_{ii}$ son las funciones de base para la línea cúbica Hermite.

La siguiente implementación de JavaScript toma un conjunto de datos y produce una función interpoladora spline cúbica monótona:

/*
 * Monotone cubic spline interpolation
 * Usage example listed at bottom; this is a fully-functional package. For
 * example, this can be executed either at sites like
 * https://www.programiz.com/javascript/online-compiler/
 * or using nodeJS.
 */
function DEBUG(s) {
    /* Uncomment the following to enable verbose output of the solver: */
    //console.log(s);
}
var j = 0;
var createInterpolant = function(xs, ys) {
    var i, length = xs.length;
    
    // Deal with length issues
    if (length != ys.length) { throw 'Need an equal count of xs and ys.'; }
    if (length === 0) { return function(x) { return 0; }; }
    if (length === 1) {
        // Impl: Precomputing the result prevents problems if ys is mutated later and allows garbage collection of ys
        // Impl: Unary plus properly converts values to numbers
        var result = +ys[0];
        return function(x) { return result; };
    }
    
    // Rearrange xs and ys so that xs is sorted
    var indexes = [];
    for (i = 0; i < length; i++) { indexes.push(i); }
    indexes.sort(function(a, b) { return xs[a] < xs[b] ? -1 : 1; });
    var oldXs = xs, oldYs = ys;
    // Impl: Creating new arrays also prevents problems if the input arrays are mutated later
    xs = []; ys = [];
    // Impl: Unary plus properly converts values to numbers
    for (i = 0; i < length; i++) { xs.push(+oldXs[indexes[i]]); ys.push(+oldYs[indexes[i]]); }

    DEBUG("debug: xs = [ " + xs + " ]")
    DEBUG("debug: ys = [ " + ys + " ]")
    
    // Get consecutive differences and slopes
    var dys = [], dxs = [], ms = [];
    for (i = 0; i < length - 1; i++) {
        var dx = xs[i + 1] - xs[i], dy = ys[i + 1] - ys[i];
        dxs.push(dx); dys.push(dy); ms.push(dy/dx);
    }
    // Get degree-1 coefficients
    var c1s = [ms[0]];
    for (i = 0; i < dxs.length - 1; i++) {
        var m = ms[i], mNext = ms[i + 1];
        if (m*mNext <= 0) {
            c1s.push(0);
        } else {
            var dx_ = dxs[i], dxNext = dxs[i + 1], common = dx_ + dxNext;
            c1s.push(3*common/((common + dxNext)/m + (common + dx_)/mNext));
        }
    }
    c1s.push(ms[ms.length - 1]);

    DEBUG("debug: dxs = [ " + dxs + " ]")
    DEBUG("debug: ms = [ " + ms + " ]")
    DEBUG("debug: c1s.length = " + c1s.length)
    DEBUG("debug: c1s = [ " + c1s + " ]")
    
    // Get degree-2 and degree-3 coefficients
    var c2s = [], c3s = [];
    for (i = 0; i < c1s.length - 1; i++) {
        var c1 = c1s[i];
        var m_ = ms[i];
        var invDx = 1/dxs[i];
        var common_ = c1 + c1s[i + 1] - m_ - m_;
        DEBUG("debug: " + i + ". c1 = " + c1);
        DEBUG("debug: " + i + ". m_ = " + m_);
        DEBUG("debug: " + i + ". invDx = " + invDx);
        DEBUG("debug: " + i + ". common_ = " + common_);
        c2s.push((m_ - c1 - common_)*invDx);
        c3s.push(common_*invDx*invDx);
    }
    DEBUG("debug: c2s = [ " + c2s + " ]")
    DEBUG("debug: c3s = [ " + c3s + " ]")

    // Return interpolant function
    return function(x) {
        // The rightmost point in the dataset should give an exact result
        var i = xs.length - 1;
        //if (x == xs[i]) { return ys[i]; }
        
        // Search for the interval x is in, returning the corresponding y if x is one of the original xs
        var low = 0, mid, high = c3s.length - 1, rval, dval;
        while (low <= high) {
            mid = Math.floor(0.5*(low + high));
            var xHere = xs[mid];
            if (xHere < x) { low = mid + 1; }
            else if (xHere > x) { high = mid - 1; }
            else {
                j++;
                i = mid;
                var diff = x - xs[i];
                rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
                dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
                DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
                return [ rval, dval ];
            }
        }
        i = Math.max(0, high);

        // Interpolate
        var diff = x - xs[i];
        j++;
        rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
        dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
        DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
        return [ rval, dval ];
    };
};

/*
   Usage example below will approximate x^2 for 0 <= x <= 4.

   Command line usage example (requires installation of nodejs):
   node monotone-cubic-spline.js
*/

var X = [0, 1, 2, 3, 4];
var F = [0, 1, 4, 9, 16];
var f = createInterpolant(X,F);
var N = X.length;
console.log("# BLOCK 0:: Data for monotone-cubic-spline.js");
console.log("X" + "\t" + "F");
for (var i = 0; i < N; i += 1) {
    console.log(F[i] + '\t' + X[i]);
}
console.log(" ");
console.log(" ");
console.log("# BLOCK 1:: Interpolated data for monotone-cubic-spline.js");
console.log("      x       " + "\t\t" + "     P(x)      " + "\t\t" + "    dP(x)/dx     ");
var message = '';
var M = 25;
for (var i = 0; i <= M; i += 1) {
    var x = X[0] + (X[N-1]-X[0])*i/M;
    var rvals = f(x);
    var P = rvals[0];
    var D = rvals[1];
    message += x.toPrecision(15) + '\t' + P.toPrecision(15) + '\t' + D.toPrecision(15) + '\n';
}
console.log(message);

• Fritsch, F. N.; Carlson, R. E. (1980). "Monotone Piecewise Cubic Interpolation". SIAM Journal on Numerical Analysis. 17 2). SIAM: 238 –246. doi:10.1137/0717021.
• Dougherty, R.L.; Edelman, A.; Hyman, J.M. (abril de 1989). "Positividad-, monotónica-, o convexidad-preservando interpolación cúbica y quintica hermita". Matemáticas de la computación. 52 (186): 471 –494. doi:10.2307/2008477.

• GPLv2 licensed Aplicación C++: MonotCubicInterpolator.cpp MonotCubicInterpolator.hpp