Interferometría
La interferometría es una técnica que utiliza la interferencia de ondas superpuestas para extraer información. La interferometría suele utilizar ondas electromagnéticas y es una técnica de investigación importante en los campos de la astronomía, la fibra óptica, la ingeniería metrológica, la metrología óptica, la oceanografía, la sismología, la espectroscopia (y sus aplicaciones a la química), la mecánica cuántica, la física nuclear y de partículas, la física del plasma, teledetección, interacciones biomoleculares, perfilado de superficies, microfluídica, medición de tensión/deformación mecánica, velocimetría, optometría y creación de hologramas.
Los interferómetros son dispositivos que extraen información de las interferencias. Son ampliamente utilizados en la ciencia y la industria para la medición de desplazamientos microscópicos, cambios en el índice de refracción e irregularidades superficiales. En el caso de la mayoría de los interferómetros, la luz de una sola fuente se divide en dos haces que viajan en diferentes caminos ópticos, que luego se combinan nuevamente para producir interferencia; Sin embargo, también se pueden hacer que dos fuentes incoherentes interfieran en algunas circunstancias. Las franjas de interferencia resultantes dan información sobre la diferencia en las longitudes de los caminos ópticos. En la ciencia analítica, los interferómetros se utilizan para medir la longitud y la forma de los componentes ópticos con precisión nanométrica; son los instrumentos de medición de longitud de mayor precisión que existen. En la espectroscopia de transformada de Fourier, se utilizan para analizar la luz que contiene características de absorción o emisión asociadas con una sustancia o mezcla. Un interferómetro astronómico consiste en dos o más telescopios separados que combinan sus señales, ofreciendo una resolución equivalente a la de un telescopio de diámetro igual a la mayor separación entre sus elementos individuales.
Principios básicos
La interferometría utiliza el principio de superposición para combinar ondas de una manera que hará que el resultado de su combinación tenga alguna propiedad significativa que diagnostique el estado original de las ondas. Esto funciona porque cuando se combinan dos ondas con la misma frecuencia, el patrón de intensidad resultante está determinado por la diferencia de fase entre las dos ondas: las ondas que están en fase sufrirán una interferencia constructiva, mientras que las ondas que están fuera de fase sufrirán una interferencia destructiva. Las ondas que no están completamente en fase ni completamente desfasadas tendrán un patrón de intensidad intermedia, que se puede utilizar para determinar su diferencia de fase relativa. La mayoría de los interferómetros usan luz o alguna otra forma de onda electromagnética.
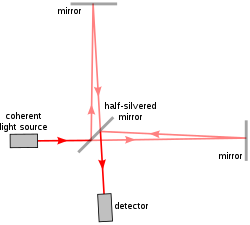
Normalmente (consulte la figura 1, la conocida configuración de Michelson), un único haz entrante de luz coherente se dividirá en dos haces idénticos mediante un divisor de haz (un espejo parcialmente reflectante). Cada uno de estos haces recorre una ruta diferente, llamada trayectoria, y se recombinan antes de llegar a un detector. La diferencia de trayectoria, la diferencia en la distancia recorrida por cada haz, crea una diferencia de fase entre ellos. Es esta diferencia de fase introducida la que crea el patrón de interferencia entre las ondas inicialmente idénticas. Si un solo haz se ha dividido a lo largo de dos caminos, entonces la diferencia de fase es un diagnóstico de cualquier cosa que cambie la fase a lo largo de los caminos. Esto podría ser un cambio físico en la longitud del camino o un cambio en el índice de refracción a lo largo del camino.
Como se ve en las Fig. 2a y 2b, el observador tiene una vista directa del espejo M1 visto a través del divisor de haz y ve una imagen reflejada M′2 de espejo M2. Las franjas pueden interpretarse como el resultado de la interferencia entre la luz procedente de las dos imágenes virtuales S′1 y S′2 de la fuente original S. Las características del patrón de interferencia dependen de la naturaleza de la fuente de luz y la orientación precisa de los espejos y el divisor de haz. En la Fig. 2a, los elementos ópticos están orientados de modo que S′1 y S′2 estén alineados con el observador, y el patrón de interferencia resultante consta de círculos centrados en la normal a M1 y M'2. Si, como en la Fig. 2b, M1 y M′2 están inclinados entre sí, las franjas de interferencia generalmente tomarán la forma de secciones cónicas (hipérbolas), pero si M′1 y M′2 superposición, las franjas cerca del eje serán rectas, paralelas e igualmente espaciadas. Si S es una fuente extendida en lugar de una fuente puntual como se ilustra, las franjas de la Fig. 2a deben observarse con un telescopio colocado en el infinito, mientras que las franjas de la Fig. 2b se localizarán en los espejos.
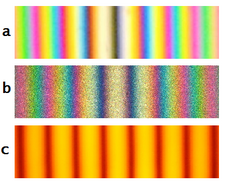
El uso de luz blanca dará como resultado un patrón de franjas de colores (ver Fig. 3). La franja central que representa la misma longitud del camino puede ser clara u oscura según el número de inversiones de fase experimentadas por los dos haces a medida que atraviesan el sistema óptico. (Ver interferómetro de Michelson para una discusión de esto.)
Categorías
Los interferómetros y las técnicas interferométricas pueden clasificarse según una variedad de criterios:
Detección homodina frente a heterodina
En la detección homodina, la interferencia se produce entre dos haces de la misma longitud de onda (o frecuencia portadora). La diferencia de fase entre los dos haces da como resultado un cambio en la intensidad de la luz en el detector. Se mide la intensidad resultante de la luz después de mezclar estos dos haces, o se observa o registra el patrón de franjas de interferencia. La mayoría de los interferómetros discutidos en este artículo pertenecen a esta categoría.
La técnica heterodina se usa para (1) cambiar una señal de entrada a un nuevo rango de frecuencia y (2) amplificar una señal de entrada débil (suponiendo que se usa un mezclador activo). Una señal de entrada débil de frecuencia f1 se mezcla con una frecuencia de referencia fuerte f2 de un oscilador local (LO). La combinación no lineal de las señales de entrada crea dos nuevas señales, una en la suma f1 + f2 de las dos frecuencias, y la otra en la diferencia f 1 − f2. Estas nuevas frecuencias se denominan heterodinas. Por lo general, solo se desea una de las nuevas frecuencias y la otra señal se filtra de la salida del mezclador. La señal de salida tendrá una intensidad proporcional al producto de las amplitudes de las señales de entrada.
La aplicación más importante y ampliamente utilizada de la técnica heterodina es el receptor superheterodino (superhet), inventado en 1917-18 por el ingeniero estadounidense Edwin Howard Armstrong y el ingeniero francés Lucien Lévy. En este circuito, la señal de radiofrecuencia entrante de la antena se mezcla con una señal de un oscilador local (LO) y se convierte mediante la técnica heterodina en una señal de frecuencia fija más baja llamada frecuencia intermedia (IF). Esta FI es amplificada y filtrada, antes de ser aplicada a un detector que extrae la señal de audio, la cual es enviada al altavoz.
- La detección de heterodinas ópticas es una extensión de la técnica heterodina a frecuencias superiores (visibles).
Si bien la interferometría óptica heterodina generalmente se realiza en un solo punto, también es posible realizar este campo amplio.
Doble camino versus camino común
Un interferómetro de doble camino es aquel en el que el haz de referencia y el haz de muestra viajan a lo largo de caminos divergentes. Los ejemplos incluyen el interferómetro de Michelson, el interferómetro de Twyman-Green y el interferómetro de Mach-Zehnder. Después de ser perturbado por la interacción con la muestra bajo prueba, el haz de muestra se recombina con el haz de referencia para crear un patrón de interferencia que luego puede interpretarse.
Un interferómetro de ruta común es una clase de interferómetro en el que el haz de referencia y el haz de muestra viajan a lo largo de la misma ruta. La figura 4 ilustra el interferómetro de Sagnac, el giroscopio de fibra óptica, el interferómetro de difracción puntual y el interferómetro de corte lateral. Otros ejemplos de interferómetro de camino común incluyen el microscopio de contraste de fase Zernike, el biprisma de Fresnel, el Sagnac de área cero y el interferómetro de placa de dispersión.
División de frente de onda y división de amplitud
Inferómetros de división de frente de onda
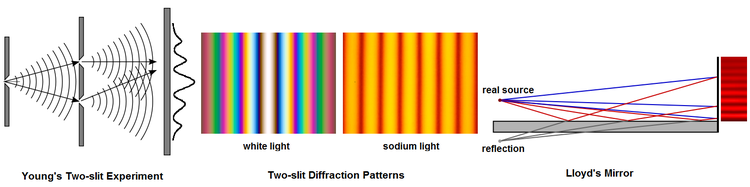
Un interferómetro divisor de frente de onda divide un frente de onda de luz que emerge de un punto o una rendija estrecha (es decir, luz espacialmente coherente) y, después de permitir que las dos partes del frente de onda viajen a través de diferentes caminos, les permite recombinar La figura 5 ilustra el experimento de interferencia de Young y el espejo de Lloyd. Otros ejemplos de interferómetro de división de frente de onda incluyen el biprisma de Fresnel, el Billet Bi-Lens y el interferómetro de Rayleigh.
En 1803, el experimento de interferencia de Young desempeñó un papel importante en la aceptación general de la teoría ondulatoria de la luz. Si se usa luz blanca en el experimento de Young, el resultado es una banda central blanca de interferencia constructiva que corresponde a la misma longitud del camino desde las dos rendijas, rodeada por un patrón simétrico de franjas de colores de intensidad decreciente. Además de la radiación electromagnética continua, el experimento de Young se ha realizado con fotones individuales, con electrones y con moléculas de buckyball lo suficientemente grandes como para verse bajo un microscopio electrónico.
El espejo de Lloyd genera franjas de interferencia al combinar la luz directa de una fuente (líneas azules) y la luz de la imagen reflejada de la fuente (líneas rojas) de un espejo sostenido con una incidencia rasante. El resultado es un patrón asimétrico de flecos. La banda de igual longitud de trayectoria, más cercana al espejo, es más oscura que brillante. En 1834, Humphrey Lloyd interpretó este efecto como prueba de que la fase de un haz reflejado en la superficie frontal está invertida.
Inferómetros divisores de amplitud
Un interferómetro de división de amplitud utiliza un reflector parcial para dividir la amplitud de la onda incidente en haces separados que se separan y se recombinan.
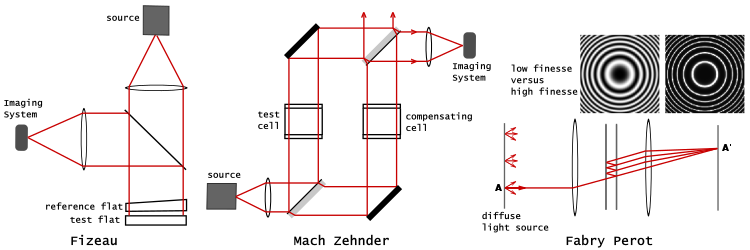
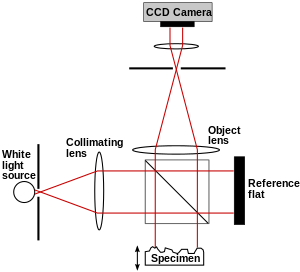
El interferómetro de Fizeau se muestra tal como podría configurarse para probar un plano óptico. Se coloca un plano de referencia calculado con precisión sobre el plano que se está probando, separado por espaciadores estrechos. El plano de referencia está ligeramente biselado (solo se necesita una fracción de grado de biselado) para evitar que la superficie posterior del plano produzca franjas de interferencia. La separación de los planos de prueba y de referencia permite que los dos planos se inclinen entre sí. Al ajustar la inclinación, que agrega un gradiente de fase controlado al patrón de franjas, se puede controlar el espaciado y la dirección de las franjas, de modo que se puede obtener una serie fácilmente interpretada de franjas casi paralelas en lugar de un remolino complejo de líneas de contorno. Sin embargo, la separación de las placas requiere que la luz de iluminación sea colimada. La figura 6 muestra un haz colimado de luz monocromática que ilumina los dos planos y un divisor de haz que permite ver las franjas en el eje.
El interferómetro de Mach-Zehnder es un instrumento más versátil que el interferómetro de Michelson. Cada uno de los caminos de luz bien separados se recorre solo una vez, y las franjas se pueden ajustar para que se localicen en cualquier plano deseado. Por lo general, las franjas se ajustarán para que queden en el mismo plano que el objeto de prueba, de modo que las franjas y el objeto de prueba se puedan fotografiar juntos. Si se decide producir franjas en luz blanca, entonces, dado que la luz blanca tiene una longitud de coherencia limitada, del orden de micrómetros, se debe tener mucho cuidado para igualar los caminos ópticos o no se verán franjas. Como se ilustra en la Fig. 6, se colocaría una celda de compensación en la trayectoria del haz de referencia para que coincida con la celda de prueba. Tenga en cuenta también la orientación precisa de los divisores de haz. Las superficies reflectantes de los divisores de haz estarían orientadas de modo que los haces de prueba y de referencia atraviesen la misma cantidad de vidrio. En esta orientación, los haces de prueba y de referencia experimentan dos reflexiones en la superficie frontal, lo que da como resultado el mismo número de inversiones de fase. El resultado es que la luz que viaja por un camino óptico de igual longitud en los haces de prueba y de referencia produce una franja de luz blanca de interferencia constructiva.
El corazón del interferómetro Fabry-Pérot es un par de planos ópticos de vidrio parcialmente plateado espaciados entre varios milímetros y centímetros con las superficies plateadas una frente a la otra. (Alternativamente, un Fabry-Pérot etalon usa una placa transparente con dos superficies reflectantes paralelas.) Al igual que con el interferómetro de Fizeau, los planos están ligeramente biselados. En un sistema típico, la iluminación la proporciona una fuente difusa colocada en el plano focal de una lente colimadora. Una lente de enfoque produce lo que sería una imagen invertida de la fuente si los pares planos no estuvieran presentes, es decir, en ausencia de los pares planos, toda la luz emitida desde el punto A que pasa a través del sistema óptico se enfocaría en el punto A'. En la Fig. 6, solo se traza un rayo emitido desde el punto A en la fuente. A medida que el rayo pasa a través de los pares planos, se refleja de forma múltiple para producir múltiples rayos transmitidos que son recogidos por la lente de enfoque y llevados al punto A&39; en la pantalla. El patrón de interferencia completo toma la apariencia de un conjunto de anillos concéntricos. La nitidez de los anillos depende de la reflectividad de los planos. Si la reflectividad es alta, lo que da como resultado un factor Q alto (es decir, mucha delicadeza), la luz monocromática produce un conjunto de anillos estrechos y brillantes sobre un fondo oscuro. En la Fig. 6, la imagen de baja delicadeza corresponde a una reflectividad de 0,04 (es decir, superficies no plateadas) frente a una reflectividad de 0,95 para la imagen de alta delicadeza.
fig. 6 ilustra los interferómetros de Fizeau, Mach-Zehnder y Fabry-Pérot. Otros ejemplos de interferómetro de división de amplitud incluyen el interferómetro Michelson, Twyman-Green, Laser Unequal Path y Linnik.
Michelson-Morley
Michelson y Morley (1887) y otros experimentadores tempranos que usaron técnicas interferométricas en un intento de medir las propiedades del éter luminífero, usaron luz monocromática solo para configurar inicialmente su equipo, siempre cambiando a luz blanca para las mediciones reales. La razón es que las mediciones se registraron visualmente. La luz monocromática daría como resultado un patrón de franjas uniforme. Al carecer de los medios modernos de control de la temperatura ambiental, los experimentadores lucharon con la deriva marginal continua a pesar de que el interferómetro podría instalarse en un sótano. Dado que las franjas desaparecerían ocasionalmente debido a las vibraciones del tráfico de caballos, tormentas eléctricas distantes y similares, sería fácil para un observador 'perderse'. cuando los flecos volvieron a la visibilidad. Las ventajas de la luz blanca, que producía un patrón de franjas de color distintivo, superaban con creces las dificultades de alinear el aparato debido a su longitud de baja coherencia. Este fue un ejemplo temprano del uso de la luz blanca para resolver la 'ambigüedad 2 pi'.
Aplicaciones
Física y astronomía
En física, uno de los experimentos más importantes de finales del siglo XIX fue el famoso "experimento fallido" de Michelson y Morley que proporcionó evidencia de la relatividad especial. Las repeticiones recientes del experimento de Michelson-Morley realizan mediciones heterodinas de frecuencias de latido de resonadores ópticos criogénicos cruzados. La figura 7 ilustra un experimento de resonador realizado por Müller et al. en 2003. Dos resonadores ópticos construidos con zafiro cristalino, que controlan las frecuencias de dos láseres, se colocaron en ángulo recto dentro de un criostato de helio. Un comparador de frecuencia midió la frecuencia de pulsación de las salidas combinadas de los dos resonadores. A partir de 2009, la precisión con la que se puede excluir la anisotropía de la velocidad de la luz en los experimentos con resonadores es del nivel 10−17.
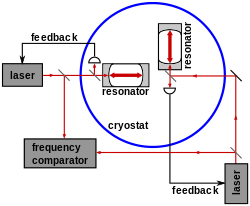 Gráfico 7. Experimento Michelson-Morley con Resonadores ópticos criogénicos | 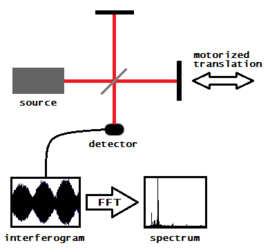 Gráfico 8. Fourier transform spectroscopy | Figura 9. Una imagen de la corona solar tomada con el coronagrama LASCO C1 |
Los interferómetros de Michelson se utilizan en filtros ópticos de banda estrecha sintonizables y como componente de hardware central de los espectrómetros de transformada de Fourier.
Cuando se utilizan como un filtro de banda estrecha sintonizable, los interferómetros de Michelson presentan una serie de ventajas y desventajas en comparación con las tecnologías de la competencia, como los interferómetros de Fabry-Pérot o los filtros de Lyot. Los interferómetros de Michelson tienen el campo de visión más grande para una longitud de onda específica y su operación es relativamente simple, ya que la sintonización se realiza mediante la rotación mecánica de las placas de ondas en lugar del control de alto voltaje de cristales piezoeléctricos o moduladores ópticos de niobato de litio como se usa en un sistema Fabry-Pérot.. En comparación con los filtros de Lyot, que utilizan elementos birrefringentes, los interferómetros de Michelson tienen una sensibilidad a la temperatura relativamente baja. En el lado negativo, los interferómetros de Michelson tienen un rango de longitud de onda relativamente restringido y requieren el uso de prefiltros que restringen la transmisión.
fig. 8 ilustra el funcionamiento de un espectrómetro de transformada de Fourier, que es esencialmente un interferómetro de Michelson con un espejo móvil. (Un espectrómetro de transformada de Fourier práctico sustituiría los espejos planos del interferómetro de Michelson convencional por reflectores de cubo de esquina, pero para simplificar, la ilustración no muestra esto). Un interferograma se genera al hacer mediciones de la señal en muchas posiciones discretas del espejo. Una transformada de Fourier convierte el interferograma en un espectro real.
fig. 9 muestra una imagen doppler de la corona solar realizada con un interferómetro sintonizable Fabry-Pérot para recuperar escaneos de la corona solar en varias longitudes de onda cerca de la línea verde FeXIV. La imagen es una imagen codificada por colores del desplazamiento Doppler de la línea, que puede estar asociada con la velocidad del plasma coronal hacia o desde la cámara satelital.
Los etalones de película delgada de Fabry-Pérot se utilizan en filtros de paso de banda estrechos capaces de seleccionar una única línea espectral para obtener imágenes; por ejemplo, la línea H-alfa o la línea Ca-K del Sol o las estrellas. La Fig. 10 muestra una imagen del Sol a 195 Ångströms (19,5 nm) del Extreme ultraviolet Imaging Telescope (EIT), que corresponde a una línea espectral de átomos de hierro multi-ionizados. EIT usó espejos reflectantes con revestimiento multicapa que estaban revestidos con capas alternas de un "espaciador" ligero. (como el silicio) y un "dispersor" elemento (como el molibdeno). Sobre cada espejo se colocaron aproximadamente 100 capas de cada tipo, con un espesor de alrededor de 10 nm cada una. Los espesores de las capas se controlaron estrictamente para que, a la longitud de onda deseada, los fotones reflejados de cada capa interfirieran constructivamente.
El Observatorio de ondas gravitacionales con interferómetro láser (LIGO) utiliza dos interferómetros Michelson-Fabry-Pérot de 4 km para la detección de ondas gravitacionales. En esta aplicación, la cavidad de Fabry-Pérot se utiliza para almacenar fotones durante casi un milisegundo mientras rebotan entre los espejos. Esto aumenta el tiempo que una onda gravitacional puede interactuar con la luz, lo que resulta en una mejor sensibilidad a bajas frecuencias. Las cavidades más pequeñas, generalmente llamadas limpiadores de modo, se utilizan para el filtrado espacial y la estabilización de frecuencia del láser principal. La primera observación de ondas gravitacionales ocurrió el 14 de septiembre de 2015.
El espacio de trabajo relativamente grande y de libre acceso del interferómetro Mach-Zehnder, y su flexibilidad para ubicar las franjas, lo han convertido en el interferómetro elegido para visualizar el flujo en túneles de viento y para los estudios de visualización de flujo en general. Se utiliza con frecuencia en los campos de la aerodinámica, la física del plasma y la transferencia de calor para medir los cambios de presión, densidad y temperatura en los gases.
Los interferómetros de Mach-Zehnder también se utilizan para estudiar una de las predicciones más contrarias a la intuición de la mecánica cuántica, el fenómeno conocido como entrelazamiento cuántico.
Un interferómetro astronómico logra observaciones de alta resolución utilizando la técnica de síntesis de apertura, mezclando señales de un grupo de telescopios comparativamente pequeños en lugar de un solo telescopio monolítico muy costoso.
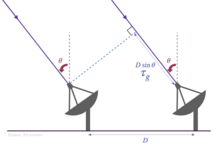
Los primeros interferómetros de los radiotelescopios usaban una línea de base única para la medición. Los interferómetros astronómicos posteriores, como el Very Large Array ilustrado en la figura 11, utilizaron conjuntos de telescopios dispuestos en un patrón en el suelo. Un número limitado de líneas de base resultará en una cobertura insuficiente. Esto se alivió usando la rotación de la Tierra para rotar la matriz en relación con el cielo. Por lo tanto, una sola línea de base podría medir la información en múltiples orientaciones tomando medidas repetidas, una técnica llamada Síntesis de rotación de la Tierra. Se lograron líneas de base de miles de kilómetros de largo usando interferometría de línea de base muy larga.
La interferometría óptica astronómica ha tenido que superar una serie de problemas técnicos que no comparte la interferometría de radiotelescopios. Las longitudes de onda cortas de la luz requieren una precisión y estabilidad extremas en la construcción. Por ejemplo, la resolución espacial de 1 milisegundo de arco requiere una estabilidad de 0,5 µm en una línea base de 100 m. Las mediciones interferométricas ópticas requieren detectores de alta sensibilidad y bajo nivel de ruido que no estuvieron disponibles hasta finales de la década de 1990. La 'visión' astronómica, la turbulencia que hace que las estrellas parpadeen, introduce cambios de fase rápidos y aleatorios en la luz entrante, lo que requiere que las tasas de recopilación de datos sean más rápidas que la tasa de turbulencia. A pesar de estas dificultades técnicas, tres instalaciones principales están ahora en funcionamiento y ofrecen resoluciones de hasta el rango de fracciones de milisegundos de arco. Este video vinculado muestra una película ensamblada a partir de imágenes de síntesis de apertura del sistema Beta Lyrae, un sistema estelar binario aproximadamente a 960 años luz (290 parsecs) de distancia en la constelación de Lyra, según lo observado por la matriz CHARA con el instrumento MIRC. El componente más brillante es la estrella primaria o donante de masa. El componente más débil es el disco grueso que rodea a la estrella secundaria, o el ganador de masa. Los dos componentes están separados por 1 milisegundo de arco. Las distorsiones de marea del donante de masa y del ganador de masa son claramente visibles.
El carácter ondulatorio de la materia se puede aprovechar para construir interferómetros. Los primeros ejemplos de interferómetros de materia fueron los interferómetros de electrones, seguidos más tarde por los interferómetros de neutrones. Alrededor de 1990 se demostraron los primeros interferómetros atómicos, seguidos más tarde por los interferómetros que emplean moléculas.
La holografía electrónica es una técnica de imagen que registra fotográficamente el patrón de interferencia de electrones de un objeto, que luego se reconstruye para producir una imagen muy ampliada del objeto original. Esta técnica se desarrolló para permitir una mayor resolución en microscopía electrónica que la que es posible utilizando técnicas de imagen convencionales. La resolución de la microscopía electrónica convencional no está limitada por la longitud de onda de los electrones, sino por las grandes aberraciones de las lentes electrónicas.
La interferometría de neutrones se ha utilizado para investigar el efecto Aharonov-Bohm, para examinar los efectos de la gravedad que actúa sobre una partícula elemental y para demostrar un comportamiento extraño de los fermiones que está en la base del principio de exclusión de Pauli: a diferencia de los objetos macroscópicos, cuando los fermiones se giran 360° alrededor de cualquier eje, no vuelven a su estado original, sino que desarrollan un signo menos en su función de onda. En otras palabras, un fermión debe girarse 720° antes de volver a su estado original.
Las técnicas de interferometría atómica están alcanzando la precisión suficiente para permitir pruebas de relatividad general a escala de laboratorio.
Los interferómetros se utilizan en física atmosférica para mediciones de alta precisión de gases traza a través de sondeos remotos de la atmósfera. Hay varios ejemplos de interferómetros que utilizan funciones de absorción o emisión de gases traza. Un uso típico sería el control continuo de la concentración de la columna de gases traza como el ozono y el monóxido de carbono por encima del instrumento.
Ingeniería y ciencia aplicada
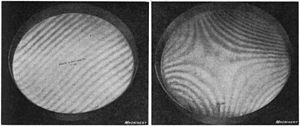
La interferometría de Newton (placa de prueba) se usa con frecuencia en la industria óptica para probar la calidad de las superficies a medida que se les da forma y figuras. La Fig. 13 muestra fotografías de pisos de referencia que se utilizan para verificar dos pisos de prueba en diferentes etapas de finalización, mostrando los diferentes patrones de franjas de interferencia. Los pisos de referencia descansan con sus superficies inferiores en contacto con los pisos de prueba, y están iluminados por una fuente de luz monocromática. Las ondas de luz reflejadas en ambas superficies interfieren, dando como resultado un patrón de bandas brillantes y oscuras. La superficie en la foto de la izquierda es casi plana, indicada por un patrón de franjas de interferencia paralelas y rectas a intervalos iguales. La superficie de la foto de la derecha es irregular, lo que da como resultado un patrón de flecos curvos. Cada par de franjas adyacentes representa una diferencia en la elevación de la superficie de la mitad de la longitud de onda de la luz utilizada, por lo que las diferencias en la elevación se pueden medir contando las franjas. La planitud de las superficies se puede medir en millonésimas de pulgada por este método. Para determinar si la superficie que se está probando es cóncava o convexa con respecto al plano óptico de referencia, se puede adoptar cualquiera de varios procedimientos. Se puede observar cómo se desplazan los flecos cuando se presiona suavemente sobre el plano superior. Si uno observa las franjas con luz blanca, la secuencia de colores se familiariza con la experiencia y ayuda en la interpretación. Finalmente, se puede comparar la apariencia de las franjas cuando se mueve la cabeza desde una posición de visualización normal a una oblicua. Este tipo de maniobras, aunque son comunes en la tienda de óptica, no son adecuadas en un entorno de prueba formal. Cuando los pisos estén listos para la venta, por lo general se montarán en un interferómetro Fizeau para realizar pruebas y certificaciones formales.
Los etalones de Fabry-Pérot se utilizan ampliamente en telecomunicaciones, láseres y espectroscopia para controlar y medir las longitudes de onda de la luz. Los filtros dicroicos son etalones de película delgada de múltiples capas. En telecomunicaciones, la multiplexación por división de longitud de onda, la tecnología que permite el uso de múltiples longitudes de onda de luz a través de una sola fibra óptica, depende de dispositivos de filtrado que son etalones de película delgada. Los láseres monomodo emplean etalones para suprimir todos los modos de cavidad óptica excepto el único de interés.
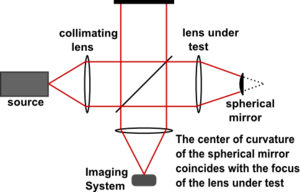
El interferómetro de Twyman-Green, inventado por Twyman y Green en 1916, es una variante del interferómetro de Michelson ampliamente utilizado para probar componentes ópticos. Las características básicas que la distinguen de la configuración de Michelson son el uso de una fuente de luz puntual monocromática y un colimador. Michelson (1918) criticó la configuración de Twyman-Green por ser inadecuada para la prueba de componentes ópticos grandes, ya que las fuentes de luz disponibles en ese momento tenían una longitud de coherencia limitada. Michelson señaló que las restricciones en la geometría impuestas por la longitud de coherencia limitada requerían el uso de un espejo de referencia del mismo tamaño que el espejo de prueba, lo que hacía que el Twyman-Green no fuera práctico para muchos propósitos. Décadas más tarde, el advenimiento de las fuentes de luz láser respondió a las objeciones de Michelson. (Un interferómetro Twyman-Green que utiliza una fuente de luz láser y una longitud de trayectoria desigual se conoce como interferómetro láser de trayectoria desigual, o LUPI). La Fig. 14 ilustra un interferómetro Twyman-Green configurado para probar una lente. La luz de una fuente puntual monocromática se expande mediante una lente divergente (no se muestra), luego se colima en un haz paralelo. Se coloca un espejo esférico convexo de modo que su centro de curvatura coincida con el foco de la lente que se está probando. El haz emergente es registrado por un sistema de imágenes para su análisis.
Los interferómetros de Mach-Zehnder se utilizan en circuitos ópticos integrados, en los que la luz interfiere entre dos ramas de una guía de ondas que se modulan externamente para variar su fase relativa. Una ligera inclinación de uno de los divisores de haz dará como resultado una diferencia de trayectoria y un cambio en el patrón de interferencia. Los interferómetros de Mach-Zehnder son la base de una amplia variedad de dispositivos, desde moduladores de RF hasta sensores e interruptores ópticos.
Los últimos telescopios astronómicos extremadamente grandes propuestos, como el Telescopio de Treinta Metros y el Telescopio Extremadamente Grande, tendrán un diseño segmentado. Sus espejos primarios se construirán a partir de cientos de segmentos de espejos hexagonales. Pulir y modelar estos segmentos de espejo altamente asféricos y sin simetría rotacional presenta un gran desafío. Los medios tradicionales de prueba óptica comparan una superficie con una referencia esférica con la ayuda de un corrector nulo. En los últimos años, los hologramas generados por computadora (CGH) han comenzado a complementar los correctores nulos en configuraciones de prueba para superficies asféricas complejas. La figura 15 ilustra cómo se hace esto. A diferencia de la figura, los CGH reales tienen un espacio entre líneas del orden de 1 a 10 µm. Cuando la luz láser pasa a través del CGH, el haz difractado de orden cero no experimenta ninguna modificación del frente de onda. Sin embargo, el frente de onda del haz difractado de primer orden se modifica para que coincida con la forma deseada de la superficie de prueba. En la configuración de prueba del interferómetro de Fizeau ilustrada, el haz difractado de orden cero se dirige hacia la superficie de referencia esférica y el haz difractado de primer orden se dirige hacia la superficie de prueba de tal manera que los dos haces reflejados se combinan para formar franjas de interferencia. Se puede usar la misma configuración de prueba para los espejos más internos que para los más externos, y solo es necesario cambiar el CGH.
Los giroscopios láser de anillo (RLG) y los giroscopios de fibra óptica (FOG) son interferómetros que se utilizan en los sistemas de navegación. Funcionan según el principio del efecto Sagnac. La distinción entre RLG y FOG es que en un RLG, todo el anillo es parte del láser, mientras que en un FOG, un láser externo inyecta haces de contrapropagación en un anillo de fibra óptica y la rotación del sistema provoca un cambio de fase relativo. entre esos rayos. En un RLG, el cambio de fase observado es proporcional a la rotación acumulada, mientras que en un FOG, el cambio de fase observado es proporcional a la velocidad angular.
En las redes de telecomunicaciones, la heterodinación se usa para mover frecuencias de señales individuales a diferentes canales que pueden compartir una sola línea de transmisión física. Esto se llama multiplexación por división de frecuencia (FDM). Por ejemplo, un cable coaxial utilizado por un sistema de televisión por cable puede transportar 500 canales de televisión al mismo tiempo porque a cada uno se le asigna una frecuencia diferente, por lo que no interfieren entre sí. Los detectores de radar Doppler de onda continua (CW) son básicamente dispositivos de detección heterodinos que comparan los haces transmitidos y reflejados.
La detección heterodina óptica se utiliza para mediciones lidar Doppler coherentes capaces de detectar luz muy débil dispersada en la atmósfera y monitorear la velocidad del viento con alta precisión. Tiene aplicación en comunicaciones de fibra óptica, en varias técnicas espectroscópicas de alta resolución, y el método autoheterodino se puede utilizar para medir el ancho de línea de un láser.
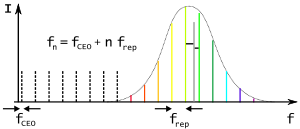
La detección heterodina óptica es una técnica esencial utilizada en mediciones de alta precisión de las frecuencias de fuentes ópticas, así como en la estabilización de sus frecuencias. Hasta hace relativamente pocos años, se necesitaban largas cadenas de frecuencia para conectar la frecuencia de microondas de una fuente de tiempo atómica de cesio u otra fuente de tiempo a frecuencias ópticas. En cada paso de la cadena, se usaría un multiplicador de frecuencia para producir un armónico de la frecuencia de ese paso, que se compararía mediante detección heterodina con el siguiente paso (la salida de una fuente de microondas, láser infrarrojo lejano, láser infrarrojo, o láser visible). Cada medición de una sola línea espectral requirió varios años de esfuerzo en la construcción de una cadena de frecuencia personalizada. Actualmente, los peines de frecuencia óptica han proporcionado un método mucho más simple para medir frecuencias ópticas. Si un láser de bloqueo de modo se modula para formar un tren de pulsos, se ve que su espectro consiste en la frecuencia portadora rodeada por un peine de frecuencias de banda lateral óptica poco espaciados con un espaciado igual a la frecuencia de repetición del pulso (Fig. 16). La frecuencia de repetición del pulso está fijada a la del estándar de frecuencia, y las frecuencias de los elementos de peine en el extremo rojo del espectro se duplican y heterodinan con las frecuencias de los elementos de peine en el extremo azul del espectro, lo que permite que el peine para servir como su propia referencia. De esta manera, el bloqueo de la salida del peine de frecuencia a un estándar atómico se puede realizar en un solo paso. Para medir una frecuencia desconocida, la salida del peine de frecuencia se dispersa en un espectro. La frecuencia desconocida se superpone con el segmento espectral apropiado del peine y se mide la frecuencia de los latidos heterodinos resultantes.
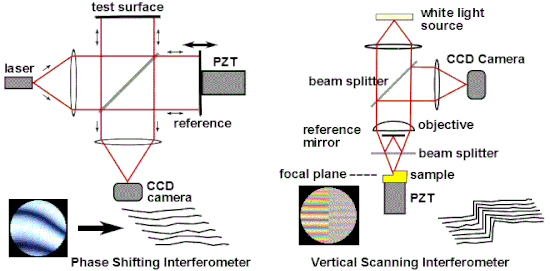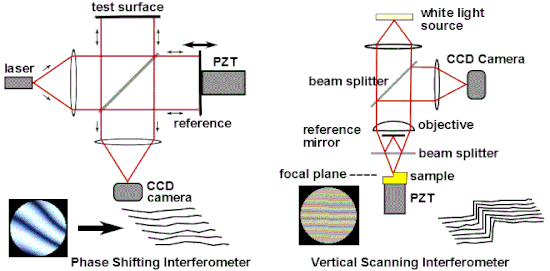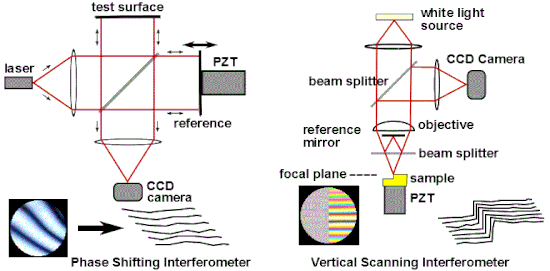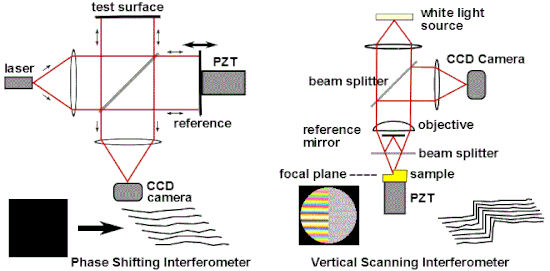
Una de las aplicaciones industriales más comunes de la interferometría óptica es como una herramienta de medición versátil para el examen de alta precisión de la topografía de la superficie. Las técnicas populares de medición interferométrica incluyen la interferometría de cambio de fase (PSI) y la interferometría de barrido vertical (VSI), también conocida como interferometría de barrido de luz blanca (SWLI) o por el término ISO Interferometría de barrido de coherencia (CSI), CSI aprovecha la coherencia para ampliar el rango de Capacidades para microscopía de interferencia. Estas técnicas se utilizan ampliamente en la fabricación microelectrónica y microóptica. PSI utiliza luz monocromática y proporciona mediciones muy precisas; sin embargo, solo se puede utilizar para superficies muy lisas. CSI a menudo usa luz blanca y aperturas numéricas altas, y en lugar de mirar la fase de las franjas, como lo hace PSI, busca la mejor posición de máximo contraste de franjas o alguna otra característica del patrón de franjas general. En su forma más simple, CSI proporciona mediciones menos precisas que PSI, pero puede usarse en superficies rugosas. Algunas configuraciones de CSI, conocidas como Enhanced VSI (EVSI), SWLI de alta resolución o análisis de dominio de frecuencia (FDA), usan efectos de coherencia en combinación con la fase de interferencia para mejorar la precisión.
La interferometría de cambio de fase aborda varios problemas asociados con el análisis clásico de interferogramas estáticos. Clásicamente, se miden las posiciones de los centros marginales. Como se ve en la Fig. 13, las desviaciones de las franjas de la rectitud y el espaciado igual brindan una medida de la aberración. Los errores al determinar la ubicación de los centros de las franjas proporcionan el límite inherente a la precisión del análisis clásico, y cualquier variación de intensidad a lo largo del interferograma también introducirá errores. Existe un equilibrio entre la precisión y la cantidad de puntos de datos: las franjas poco espaciadas proporcionan muchos puntos de datos de baja precisión, mientras que las franjas muy espaciadas proporcionan una cantidad baja de puntos de datos de alta precisión. Dado que los datos del centro marginal son todo lo que se usa en el análisis clásico, toda la otra información que teóricamente podría obtenerse mediante un análisis detallado de las variaciones de intensidad en un interferograma se descarta. Finalmente, con los interferogramas estáticos, se necesita información adicional para determinar la polaridad del frente de onda: en la Fig. 13, se puede ver que la superficie probada de la derecha se desvía de la planitud, pero no se puede saber a partir de esta imagen única si esta desviación de la planitud es cóncava o convexa. Tradicionalmente, esta información se obtendría utilizando medios no automatizados, como observando la dirección en que se mueven las franjas cuando se empuja la superficie de referencia.
La interferometría de cambio de fase supera estas limitaciones al no depender de encontrar centros marginales, sino al recopilar datos de intensidad de cada punto del sensor de imagen CCD. Como se ve en la Fig. 17, se analizan múltiples interferogramas (al menos tres) con la superficie óptica de referencia desplazada una fracción precisa de longitud de onda entre cada exposición usando un transductor piezoeléctrico (PZT). Alternativamente, se pueden introducir cambios de fase precisos modulando la frecuencia del láser. Las imágenes capturadas son procesadas por una computadora para calcular los errores del frente de onda óptico. La precisión y reproducibilidad de PSI es mucho mayor de lo que es posible en el análisis de interferograma estático, siendo rutinarias las repeticiones de medición de una centésima de longitud de onda. La tecnología de cambio de fase se ha adaptado a una variedad de tipos de interferómetros, como Twyman-Green, Mach-Zehnder, láser Fizeau e incluso configuraciones de ruta común, como interferómetros de difracción puntual y de corte lateral. En términos más generales, las técnicas de cambio de fase se pueden adaptar a casi cualquier sistema que utilice franjas para la medición, como la interferometría holográfica y de motas.
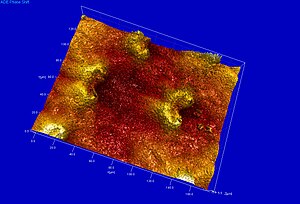
En la interferometría de barrido de coherencia, la interferencia solo se logra cuando los retrasos en la longitud de la trayectoria del interferómetro coinciden con el tiempo de coherencia de la fuente de luz. CSI monitorea el contraste de franjas en lugar de la fase de las franjas. La Fig. 17 ilustra un microscopio CSI que usa un interferómetro Mirau en el objetivo; otras formas de interferómetro utilizadas con luz blanca incluyen el interferómetro de Michelson (para objetivos de bajo aumento, donde el espejo de referencia en un objetivo Mirau interrumpiría demasiado la apertura) y el interferómetro de Linnik (para objetivos de gran aumento con distancia de trabajo limitada). La muestra (o alternativamente, el objetivo) se mueve verticalmente sobre el rango completo de altura de la muestra, y se encuentra la posición de máximo contraste de franjas para cada píxel. El principal beneficio de la interferometría de barrido de coherencia es que se pueden diseñar sistemas que no sufren la ambigüedad de 2 pi de la interferometría coherente y, como se ve en la Fig. 18, que escanea un volumen de 180 μm x 140 μm x 10 μm, es muy adecuado para la creación de perfiles. escalones y superficies rugosas. La resolución axial del sistema está determinada en parte por la longitud de coherencia de la fuente de luz. Las aplicaciones industriales incluyen metrología de superficie en proceso, medición de rugosidad, metrología de superficie 3D en espacios de difícil acceso y en entornos hostiles, perfilometría de superficies con características de alta relación de aspecto (ranuras, canales, orificios) y medición de espesor de película (semi- industrias de conductores y óptica, etc.).
fig. 19 ilustra un interferómetro Twyman-Green configurado para escanear con luz blanca un objeto macroscópico.
La interferometría holográfica es una técnica que utiliza la holografía para monitorear pequeñas deformaciones en implementaciones de una sola longitud de onda. En implementaciones de múltiples longitudes de onda, se utiliza para realizar metrología dimensional de piezas y ensamblajes grandes y para detectar defectos de superficie más grandes.
La interferometría holográfica se descubrió por accidente como resultado de errores cometidos durante la creación de hologramas. Los primeros láseres eran relativamente débiles y las placas fotográficas eran insensibles, lo que requería largas exposiciones durante las cuales podían ocurrir vibraciones o cambios diminutos en el sistema óptico. Los hologramas resultantes, que mostraban el sujeto holográfico cubierto de flecos, se consideraron arruinados.
Finalmente, varios grupos independientes de experimentadores a mediados de los 60 se dieron cuenta de que los flecos codificaban información importante sobre los cambios dimensionales que ocurrían en el sujeto y comenzaron a producir intencionalmente exposiciones dobles holográficas. El artículo principal sobre interferometría holográfica cubre las disputas sobre la prioridad del descubrimiento que ocurrieron durante la emisión de la patente para este método.
La holografía de exposición doble y múltiple es uno de los tres métodos utilizados para crear interferogramas holográficos. Una primera exposición registra el objeto en un estado no tensionado. Las exposiciones posteriores en la misma placa fotográfica se realizan mientras el objeto se somete a algún estrés. La imagen compuesta representa la diferencia entre los estados estresado y no estresado.
La holografía en tiempo real es un segundo método para crear interferogramas holográficos. Se crea un holograma del objeto no acentuado. Este holograma se ilumina con un haz de referencia para generar una imagen de holograma del objeto superpuesto directamente sobre el objeto original mientras el objeto está sujeto a alguna tensión. Las ondas del objeto de esta imagen de holograma interferirán con las nuevas ondas provenientes del objeto. Esta técnica permite monitorear en tiempo real los cambios de forma.
El tercer método, la holografía de promedio de tiempo, consiste en crear una holografía mientras el objeto se somete a una tensión o vibración periódicas. Esto produce una imagen visual del patrón de vibración.
El radar interferométrico de apertura sintética (InSAR) es una técnica de radar utilizada en geodesia y teledetección. Las imágenes satelitales de radar de apertura sintética de una característica geográfica se toman en días separados, y los cambios que han tenido lugar entre las imágenes de radar tomadas en días separados se registran como franjas similares a las obtenidas en la interferometría holográfica. La técnica puede monitorear la deformación a escala de centímetros a milímetros resultante de terremotos, volcanes y deslizamientos de tierra, y también tiene usos en ingeniería estructural, en particular para el monitoreo de hundimiento y estabilidad estructural. La figura 20 muestra el Kilauea, un volcán activo en Hawái. Los datos adquiridos con el radar de apertura sintética de banda X del transbordador espacial Endeavour el 13 de abril de 1994 y el 4 de octubre de 1994 se utilizaron para generar franjas interferométricas, que se superpusieron en la imagen X-SAR de Kilauea.
La interferometría de patrón de motas electrónicas (ESPI), también conocida como holografía de TV, utiliza detección y grabación de video para producir una imagen del objeto sobre la cual se superpone un patrón de franjas que representa el desplazamiento del objeto entre grabaciones. (ver Fig. 21) Las franjas son similares a las obtenidas en interferometría holográfica.
Cuando se inventaron los láseres por primera vez, se consideraba que el moteado láser era un grave inconveniente en el uso de láseres para iluminar objetos, especialmente en imágenes holográficas debido a la imagen granulada que se producía. Más tarde se descubrió que los patrones de motas podían transmitir información sobre las deformaciones de la superficie del objeto. Butters y Leendertz desarrollaron la técnica de la interferometría de patrón moteado en 1970 y, desde entonces, el moteado se ha explotado en una variedad de otras aplicaciones. Se toma una fotografía del patrón moteado antes de la deformación y se toma una segunda fotografía del patrón moteado después de la deformación. La resta digital de las dos imágenes da como resultado un patrón de franjas de correlación, donde las franjas representan líneas de igual deformación. Se pueden usar pulsos de láser cortos en el rango de nanosegundos para capturar eventos transitorios muy rápidos. Existe un problema de fase: en ausencia de otra información, no se puede diferenciar entre las líneas de contorno que indican un pico frente a las líneas de contorno que indican un valle. Para resolver el problema de la ambigüedad de fase, ESPI puede combinarse con métodos de cambio de fase.
Un método para establecer líneas de base geodésicas precisas, inventado por Yrjö Väisälä, aprovechó la longitud de baja coherencia de la luz blanca. Inicialmente, la luz blanca se dividía en dos, con el haz de referencia 'doblado', rebotando de un lado a otro seis veces entre un par de espejos separados exactamente por 1 m. Solo si la ruta de prueba fuera exactamente 6 veces la ruta de referencia, se verían las franjas. Las aplicaciones repetidas de este procedimiento permitieron la medición precisa de distancias de hasta 864 metros. Las líneas de base así establecidas se utilizaron para calibrar el equipo de medición de distancias geodésicas, lo que condujo a una escala rastreable metrológicamente para las redes geodésicas medidas por estos instrumentos. (Este método ha sido reemplazado por GPS).
Otros usos de los interferómetros han sido el estudio de la dispersión de materiales, la medición de índices de refracción complejos y las propiedades térmicas. También se utilizan para el mapeo de movimiento tridimensional, incluido el mapeo de patrones vibratorios de estructuras.
Biología y medicina
La interferometría óptica, aplicada a la biología y la medicina, proporciona capacidades de metrología sensible para la medición de biomoléculas, componentes subcelulares, células y tejidos. Muchas formas de biosensores sin etiquetas se basan en la interferometría porque la interacción directa de los campos electromagnéticos con la polarizabilidad molecular local elimina la necesidad de etiquetas fluorescentes o marcadores de nanopartículas. A mayor escala, la interferometría celular comparte aspectos con la microscopía de contraste de fase, pero comprende una clase mucho mayor de configuraciones ópticas sensibles a la fase que se basan en la interferencia óptica entre los constituyentes celulares a través de la refracción y la difracción. A escala de tejido, la propagación de la luz dispersada hacia adelante parcialmente coherente a través de las microaberraciones y la heterogeneidad de la estructura del tejido brinda oportunidades para utilizar la activación sensible a la fase (tomografía de coherencia óptica), así como la espectroscopia de fluctuación sensible a la fase para obtener imágenes de propiedades estructurales y dinámicas sutiles..
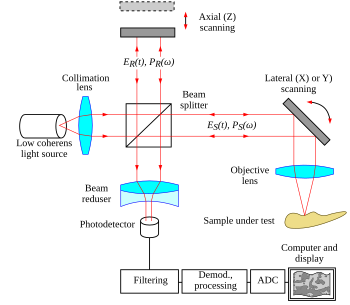 Figura 22. Configuración óptica típica del punto único OCT |  Figura 23. Retinopatía serosa central, imaginada utilizando tomografía de la coherencia óptica |
La tomografía de coherencia óptica (OCT) es una técnica de imagen médica que utiliza interferometría de baja coherencia para proporcionar una visualización tomográfica de las microestructuras tisulares internas. Como se ve en la Fig. 22, el núcleo de un sistema OCT típico es un interferómetro de Michelson. Un brazo de interferómetro se enfoca en la muestra de tejido y escanea la muestra en un patrón de trama longitudinal X-Y. El otro brazo del interferómetro rebota en un espejo de referencia. La luz reflejada de la muestra de tejido se combina con la luz reflejada de la referencia. Debido a la baja coherencia de la fuente de luz, la señal interferométrica se observa solo en una profundidad limitada de la muestra. Por lo tanto, el escaneo X-Y registra un corte óptico delgado de la muestra a la vez. Al realizar múltiples escaneos, moviendo el espejo de referencia entre cada escaneo, se puede reconstruir una imagen tridimensional completa del tejido. Los avances recientes se han esforzado por combinar la recuperación de fase nanométrica de la interferometría coherente con la capacidad de rango de la interferometría de baja coherencia.
La microscopía de contraste de fase y contraste de interferencia diferencial (DIC) son herramientas importantes en biología y medicina. La mayoría de las células animales y los organismos unicelulares tienen muy poco color y sus orgánulos intracelulares son casi totalmente invisibles bajo una simple iluminación de campo brillante. Estas estructuras pueden hacerse visibles tiñendo las muestras, pero los procedimientos de tinción consumen mucho tiempo y matan las células. Como se ve en las Figs. 24 y 25, los microscopios de contraste de fase y DIC permiten estudiar células vivas sin teñir. DIC también tiene aplicaciones no biológicas, por ejemplo, en el análisis del procesamiento de semiconductores de silicio plano.
La interferometría de baja coherencia con resolución angular (a/LCI) utiliza luz dispersa para medir los tamaños de los objetos subcelulares, incluidos los núcleos celulares. Esto permite combinar las mediciones de profundidad de interferometría con las mediciones de densidad. Se han encontrado varias correlaciones entre el estado de salud de los tejidos y las medidas de los objetos subcelulares. Por ejemplo, se ha descubierto que a medida que el tejido cambia de normal a canceroso, aumenta el tamaño medio de los núcleos celulares.
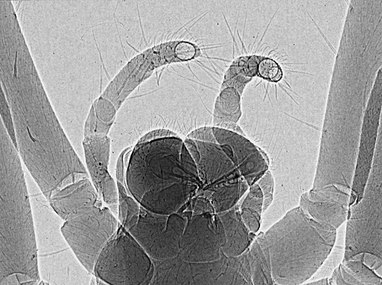
Las imágenes de rayos X con contraste de fase (Fig. 26) se refieren a una variedad de técnicas que usan información de fase de un haz de rayos X coherente para obtener imágenes de los tejidos blandos. (Para una discusión elemental, consulte Imágenes de rayos X de contraste de fase (introducción). Para una revisión más detallada, consulte Imágenes de rayos X de contraste de fase). Se ha convertido en un método importante para visualizar estructuras celulares e histológicas en un amplia gama de estudios biológicos y médicos. Hay varias tecnologías que se utilizan para obtener imágenes de contraste de fase de rayos X, y todas utilizan diferentes principios para convertir las variaciones de fase en los rayos X que emergen de un objeto en variaciones de intensidad. Estos incluyen contraste de fase basado en propagación, interferometría de Talbot, interferometría de campo lejano basada en Moiré, imágenes mejoradas por refracción e interferometría de rayos X. Estos métodos proporcionan un mayor contraste en comparación con las imágenes de rayos X de contraste de absorción normales, lo que permite ver detalles más pequeños. Una desventaja es que estos métodos requieren equipos más sofisticados, como fuentes de rayos X de sincrotrón o microfoco, óptica de rayos X o detectores de rayos X de alta resolución.
Contenido relacionado
Objeto (informática)
Lockheed Martin
Eugenio wigner