Interferencia de ondas

La interferencia de dos olas. Cuando en fase, las dos ondas inferiores crean injerencia constructiva (izquierda), resultando en una ola de amplitud agregada. Cuando 180° fuera de fase, crean interferencia (derecha), resultando en una ola de amplitud cero.

En física, interferencia es un fenómeno en el que dos ondas se combinan sumando su desplazamiento en cada punto del espacio y el tiempo, para formar una onda resultante de mayor, menor o igual amplitud.. Las interferencias constructivas y destructivas resultan de la interacción de ondas que están correlacionadas o son coherentes entre sí, ya sea porque provienen de la misma fuente o porque tienen el mismo o casi el mismo misma frecuencia. Los efectos de interferencia se pueden observar con todo tipo de ondas, por ejemplo, ondas luminosas, de radio, acústicas, de agua superficial, ondas de gravedad u ondas de materia.

Etimología

La palabra interferencia se deriva de las palabras latinas inter que significa "entre" y fere que significa "golpear o golpear", y fue acuñado por Thomas Young en 1801.

Mecanismos

Interferencia de las ondas de viaje derecho (verde) y de viaje izquierdo (azul) en espacio bidimensional, dando lugar a onda final (rojo)

Interferencia de olas de dos fuentes de puntos.

El principio de superposición de ondas establece que cuando dos o más ondas del mismo tipo que se propagan inciden en el mismo punto, la amplitud resultante en ese punto es igual a la suma vectorial de las amplitudes de las ondas individuales. Si la cresta de una onda se encuentra con la cresta de otra onda de la misma frecuencia en el mismo punto, entonces la amplitud es la suma de las amplitudes individuales; esto es interferencia constructiva. Si la cresta de una onda se encuentra con el valle de otra onda, entonces la amplitud es igual a la diferencia en las amplitudes individuales; esto se conoce como interferencia destructiva. En medios ideales (el agua, el aire son casi ideales) la energía siempre se conserva, en los puntos de interferencia destructiva la energía se almacena en la elasticidad del medio. Por ejemplo, cuando dejamos caer 2 guijarros en un estanque, vemos un patrón, pero eventualmente las olas continúan y solo cuando llegan a la orilla, la energía se absorbe del medio.

Una imagen magnificada de un patrón de interferencia de colores en una película de jabón. Los "agujeros negros" son áreas de interferencia casi total destructiva (antifase).

La interferencia constructiva ocurre cuando la diferencia de fase entre las ondas es un múltiplo par de π (180°), mientras que la interferencia destructiva ocurre cuando la diferencia es un múltiplo impar de π. Si la diferencia entre las fases es intermedia entre estos dos extremos, entonces la magnitud del desplazamiento de las ondas sumadas se encuentra entre los valores mínimo y máximo.

Considere, por ejemplo, lo que sucede cuando dos piedras idénticas se dejan caer en un charco de agua tranquila en diferentes lugares. Cada piedra genera una onda circular que se propaga hacia afuera desde el punto donde se dejó caer la piedra. Cuando las dos ondas se superponen, el desplazamiento neto en un punto particular es la suma de los desplazamientos de las ondas individuales. En algunos puntos, estos estarán en fase, y producirán un desplazamiento máximo. En otros lugares, las olas estarán en antifase y no habrá desplazamiento neto en estos puntos. Por lo tanto, partes de la superficie serán estacionarias; estas se ven en la figura de arriba y a la derecha como líneas estacionarias de color azul verdoso que irradian desde el centro.

La interferencia de la luz es un fenómeno único en el que nunca podemos observar la superposición del campo EM directamente como podemos, por ejemplo, en el agua. La superposición en el campo EM es un requisito asumido y necesario, fundamentalmente 2 haces de luz se atraviesan y continúan en sus respectivos caminos. La luz se puede explicar clásicamente por la superposición de ondas, sin embargo, una comprensión más profunda de la interferencia de la luz requiere un conocimiento de la dualidad de onda-partícula de la luz que se debe a la mecánica cuántica. Los principales ejemplos de interferencia de la luz son el famoso experimento de la doble rendija, el moteado láser, los revestimientos antirreflectantes y los interferómetros. Tradicionalmente, el modelo de onda clásico se enseña como base para comprender la interferencia óptica, según el principio de Huygens-Fresnel; sin embargo, existe una explicación basada en la integral de trayectoria de Feynman que tiene en cuenta consideraciones de mecánica cuántica.

Derivación

Lo anterior se puede demostrar en una dimensión al derivar la fórmula para la suma de dos ondas. La ecuación para la amplitud de una onda sinusoidal que viaja hacia la derecha a lo largo del eje x es

W1()x,t)=A#⁡ ⁡ ()kx− − ⋅ ⋅ t){displaystyle W_{1}(x,t)=Acos(kx-omega t)}

A{displaystyle A}

k=2π π /λ λ {displaystyle k=2pi /lambda }

⋅ ⋅ =2π π f{displaystyle omega =2pi f}

W2()x,t)=A#⁡ ⁡ ()kx− − ⋅ ⋅ t+φ φ ){displaystyle W_{2}(x,t)=Acos(kx-omega t+varphi)}

φ φ {displaystyle varphi }

W1+W2=A[#⁡ ⁡ ()kx− − ⋅ ⋅ t)+#⁡ ⁡ ()kx− − ⋅ ⋅ t+φ φ )].{displaystyle W_{1}+W_{2}=A[cos(kx-omega t)+cos(kx-omega t+varphi)].}

#⁡ ⁡ a+#⁡ ⁡ b=2#⁡ ⁡ ()a− − b2)#⁡ ⁡ ()a+b2),{textstyle cos a+cos b=2cos left({a-b over 2}right)cos left({a+b over 2}right),}

W1+W2=2A#⁡ ⁡ ()φ φ 2)#⁡ ⁡ ()kx− − ⋅ ⋅ t+φ φ 2).{displaystyle W_{1}+W_{2}=2Acos left({varphi over 2}right)cos left(kx-omega t+{varphi over 2}right). }

φ φ /2{displaystyle varphi /2}

• Interferencia constructiva: Si la diferencia de fase es incluso múltiple π: φ φ =...... ,− − 4π π ,− − 2π π ,0,2π π ,4π π ,...... {displaystyle varphi =ldots-4pi-2pi0,2pi4pi4ldots } entonces Silencio#⁡ ⁡ ()φ φ /2)Silencio=1{displaystyle left pacienciacos(varphi /2)right sobre la vida=1}, así que la suma de las dos ondas es una onda con el doble de amplitud
  W1+W2=2A#⁡ ⁡ ()kx− − ⋅ ⋅ t){displaystyle W_{1}+W_{2}=2Acos(kx-omega t)}

  
• Interferencia destructiva: Si la diferencia de fase es un número impar de π: φ φ =...... ,− − 3π π ,− − π π ,π π ,3π π ,5π π ,...... {displaystyle varphi =ldots-3pi,-pi,pi,3pi,5pildots} entonces #⁡ ⁡ ()φ φ /2)=0{displaystyle cos(varphi /2)=0,}, así que la suma de las dos ondas es cero
  W1+W2=0{displaystyle W_{1}+W_{2}=0}

  

Entre dos ondas planas

Disposición geométrica para la interferencia de dos ondas de avión

fringes de interferencia en ondas de aviones superpuestas

Se obtiene una forma simple de patrón de interferencia si dos ondas planas de la misma frecuencia se cruzan en un ángulo. La interferencia es esencialmente un proceso de redistribución de energía. La energía que se pierde en la interferencia destructiva se recupera en la interferencia constructiva. Una onda viaja horizontalmente y la otra viaja hacia abajo en un ángulo θ con respecto a la primera onda. Suponiendo que las dos ondas están en fase en el punto B, la fase relativa cambia a lo largo del eje x. La diferencia de fase en el punto A viene dada por

Δ Δ φ φ =2π π dλ λ =2π π xpecado⁡ ⁡ Silencio Silencio λ λ .{displaystyle Delta varphi ={frac {2ccH00} ♪{lambda }={frac {2pi xsin theta ♫{lambda }}

Se puede ver que las dos ondas están en fase cuando

xpecado⁡ ⁡ Silencio Silencio λ λ =0,± ± 1,± ± 2,...... ,{displaystyle {frac {xsin theta } {lambda }=0,pm 1,pm 2,ldots}

y están medio ciclo desfasados cuando

xpecado⁡ ⁡ Silencio Silencio λ λ =± ± 12,± ± 32,...... {displaystyle {frac {xsin theta ♫{lambda }=pm {frac {1}{2}pm {frac {3}{2},ldots }

La interferencia constructiva ocurre cuando las ondas están en fase y la interferencia destructiva cuando están desfasadas medio ciclo. Así, se produce un patrón de franjas de interferencia, donde la separación de los máximos es

df=λ λ pecado⁡ ⁡ Silencio Silencio {displaystyle {f}={f} {f}{sin theta }

y d_f se conoce como espaciado marginal. El espaciado de las franjas aumenta con el aumento de la longitud de onda y con la disminución del ángulo θ.

Las franjas se observan donde las dos ondas se superponen y el espaciado de las franjas es uniforme en todas partes.

Entre dos ondas esféricas

Interferencia óptica entre dos fuentes de puntos que tienen diferentes longitudes de onda y separaciones de fuentes.

Una fuente puntual produce una onda esférica. Si la luz de dos fuentes puntuales se superpone, el patrón de interferencia muestra la forma en que la diferencia de fase entre las dos ondas varía en el espacio. Esto depende de la longitud de onda y de la separación de las fuentes puntuales. La figura de la derecha muestra la interferencia entre dos ondas esféricas. La longitud de onda aumenta de arriba hacia abajo y la distancia entre las fuentes aumenta de izquierda a derecha.

Cuando el plano de observación está lo suficientemente lejos, el patrón de franjas será una serie de líneas casi rectas, ya que las ondas serán casi planas.

Múltiples haces

La interferencia se produce cuando se suman varias ondas siempre que las diferencias de fase entre ellas permanezcan constantes durante el tiempo de observación.

A veces es deseable que varias ondas de la misma frecuencia y amplitud sumen cero (es decir, interfieran destructivamente, se cancelen). Este es el principio detrás, por ejemplo, de la energía trifásica y la rejilla de difracción. En ambos casos, el resultado se logra mediante un espaciamiento uniforme de las fases.

Es fácil ver que un conjunto de ondas cancelarán si tienen la misma amplitud y sus fases están espaciadas igualmente en ángulo. Usando fáseres, cada onda puede ser representada como Aeiφ φ n{displaystyle Ae^{ivarphi ¿Qué? para N{displaystyle N} ondas n=0{displaystyle n=0} a n=N− − 1{displaystyle n=N-1}, donde

φ φ n− − φ φ n− − 1=2π π N.{displaystyle varphi _{n}-varphi - ¿Qué? } {N}}

Para demostrar que

.. n=0N− − 1Aeiφ φ n=0{displaystyle sum _{n=0} {N-1}Ae^{ivarphi ¿Qué?

uno simplemente asume el converso, luego multiplica ambos lados por ei2π π N.{displaystyle e^{i{fc} - Sí.

El interferómetro de Fabry-Pérot utiliza la interferencia entre múltiples reflejos.

Se puede considerar que una rejilla de difracción es un interferómetro de haz múltiple; ya que los picos que produce se generan por interferencia entre la luz transmitida por cada uno de los elementos de la rejilla; consulte interferencia frente a difracción para obtener más información.

Interferencia óptica

Creación de franjas de interferencia por un plano óptico sobre una superficie reflectante. Los rayos de luz de una fuente monocromática pasan por el vidrio y reflejan tanto la superficie inferior del plano como la superficie de soporte. La pequeña brecha entre las superficies significa que los dos rayos reflejados tienen diferentes longitudes de ruta. Además, el rayo reflejado en la placa inferior sufre una reversión de fase 180°. As a result, at locations a) donde la diferencia del camino es un extraño múltiple de λ/2, las ondas refuerzan. En lugares b) donde la diferencia del camino es incluso un múltiplo de λ/2 las ondas cancelan. Puesto que la brecha entre las superficies varía ligeramente de ancho en diferentes puntos, una serie de bandas alternantes brillantes y oscuras, fring fringes, se ven.

Debido a que la frecuencia de las ondas de luz (~10¹⁴ Hz) es demasiado alta para que los detectores disponibles actualmente detecten la variación del campo eléctrico de la luz, es posible observar solo la intensidad de un patrón de interferencia óptica. La intensidad de la luz en un punto dado es proporcional al cuadrado de la amplitud media de la onda. Esto se puede expresar matemáticamente de la siguiente manera. El desplazamiento de las dos ondas en un punto r es:

U1()r,t)=A1()r)ei[φ φ 1()r)− − ⋅ ⋅ t]{displaystyle U_{1}(mathbf {r}t)=A_{1}(mathbf {r})e^{i[varphi _{1}(mathbf {r})-omega t]}}

U2()r,t)=A2()r)ei[φ φ 2()r)− − ⋅ ⋅ t]{displaystyle U_{2}(mathbf {r}t)=A_{2}(mathbf {r})e^{i[varphi _{2}(mathbf {r})-omega t]}}

donde A representa la magnitud del desplazamiento, φ representa la fase y ω representa la frecuencia angular.

El desplazamiento de las ondas sumadas es

U()r,t)=A1()r)ei[φ φ 1()r)− − ⋅ ⋅ t]+A2()r)ei[φ φ 2()r)− − ⋅ ⋅ t].{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMitbf {f}fnMitbf} {fnMitbf}(cHFF})e^{i[varphi _{2}(mathbf} {f})} {f}f} {f}f}f}f}f}fnMit]

La intensidad de la luz en r viene dada por

I()r)=∫ ∫ U()r,t)UAlternativa Alternativa ()r,t)dt∝ ∝ A12()r)+A22()r)+2A1()r)A2()r)#⁡ ⁡ [φ φ 1()r)− − φ φ 2()r)].################################################################################################################################################################################################################################################################

Esto se puede expresar en términos de las intensidades de las ondas individuales como

I()r)=I1()r)+I2()r)+2I1()r)I2()r)#⁡ ⁡ [φ φ 1()r)− − φ φ 2()r)].{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft {f}} {fnMicrosoft} {f} {f} {f}f} {cH0} {cH00}}} {b} {cH00}cH00}} {b}cH00}cH0}cH00}cH00}cH00}cH00}cH00}cH00}cH00} {cH00} {cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00} {cH00} {cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00cH00}}cH00}

Por lo tanto, el patrón de interferencia traza la diferencia de fase entre las dos ondas, con máximos que ocurren cuando la diferencia de fase es un múltiplo de 2 π. Si los dos haces tienen la misma intensidad, los máximos son cuatro veces más brillantes que los haces individuales y los mínimos tienen una intensidad cero.

Clásicamente, las dos ondas deben tener la misma polarización para dar lugar a franjas de interferencia, ya que no es posible que las ondas de diferentes polarizaciones se anulen o se sumen. En cambio, cuando se suman ondas de diferente polarización, dan lugar a una onda de diferente estado de polarización.

La mecánica cuántica, las teorías de Paul Dirac y Richard Feynman ofrecen un enfoque más moderno. Dirac demostró que cada quanta o fotón de luz actúa por sí mismo, lo que él mismo afirmó como "cada fotón interfiere consigo mismo". Richard Feynman demostró que al evaluar una integral de ruta en la que se consideran todas las rutas posibles, surgirán varias rutas de mayor probabilidad. En películas delgadas, por ejemplo, el espesor de la película que no es un múltiplo de la longitud de onda de la luz no permitirá que los cuantos atraviesen, solo es posible la reflexión.

Requisitos de la fuente de luz

La discusión anterior asume que las ondas que interfieren entre sí son monocromáticas, es decir, tienen una sola frecuencia; esto requiere que sean infinitas en el tiempo. Sin embargo, esto no es ni práctico ni necesario. Dos ondas idénticas de duración finita cuya frecuencia es fija durante ese período darán lugar a un patrón de interferencia mientras se superponen. Dos ondas idénticas que consisten en un espectro estrecho de ondas de frecuencia de duración finita (pero más corta que su tiempo de coherencia), darán una serie de patrones de franjas con espaciamientos ligeramente diferentes, y siempre que la dispersión de los espaciamientos sea significativamente menor que el espaciamiento promedio de las franjas., se observará nuevamente un patrón de franjas durante el tiempo en que las dos ondas se superponen.

Las fuentes de luz convencionales emiten ondas de diferentes frecuencias y en diferentes momentos desde diferentes puntos de la fuente. Si la luz se divide en dos ondas y luego se vuelve a combinar, cada onda de luz individual puede generar un patrón de interferencia con su otra mitad, pero los patrones de franjas individuales generados tendrán diferentes fases y espacios, y normalmente no se observará ningún patrón de franjas general.. Sin embargo, las fuentes de luz de un solo elemento, como las lámparas de vapor de sodio o mercurio, tienen líneas de emisión con espectros de frecuencia bastante estrechos. Cuando estos se filtran espacialmente y por color, y luego se dividen en dos ondas, se pueden superponer para generar franjas de interferencia. Toda la interferometría anterior a la invención del láser se realizaba utilizando dichas fuentes y tenía una amplia gama de aplicaciones exitosas.

Por lo general, un rayo láser se aproxima mucho más a una fuente monocromática y, por lo tanto, es mucho más sencillo generar franjas de interferencia con un láser. La facilidad con la que se pueden observar las franjas de interferencia con un rayo láser a veces puede causar problemas, ya que los reflejos dispersos pueden generar franjas de interferencia falsas que pueden dar lugar a errores.

Normalmente, en la interferometría se usa un solo rayo láser, aunque se ha observado interferencia al usar dos láseres independientes cuyas frecuencias coincidían lo suficiente como para satisfacer los requisitos de fase. Esto también se ha observado para la interferencia de campo amplio entre dos fuentes de láser incoherentes.

Interferencia de luz blanca en una burbuja de jabón. La iridiscencia se debe a la interferencia de suciedad fina.

También es posible observar franjas de interferencia usando luz blanca. Se puede considerar que un patrón de franjas de luz blanca está formado por un 'espectro' de patrones de flecos cada uno de espaciado ligeramente diferente. Si todos los patrones de franjas están en fase en el centro, las franjas aumentarán de tamaño a medida que disminuya la longitud de onda y la intensidad sumada mostrará tres o cuatro franjas de color variable. Young describe esto muy elegantemente en su discusión sobre la interferencia de dos rendijas. Dado que las franjas de luz blanca se obtienen solo cuando las dos ondas han recorrido distancias iguales desde la fuente de luz, pueden ser muy útiles en interferometría, ya que permiten identificar la franja de diferencia de trayectoria cero.

Arreglos ópticos

Para generar franjas de interferencia, la luz de la fuente debe dividirse en dos ondas que luego deben volver a combinarse. Tradicionalmente, los interferómetros se han clasificado como sistemas de división de amplitud o de división de frente de onda.

En un sistema de división de amplitud, se usa un divisor de haz para dividir la luz en dos haces que viajan en diferentes direcciones, que luego se superponen para producir el patrón de interferencia. El interferómetro de Michelson y el interferómetro de Mach-Zehnder son ejemplos de sistemas de división de amplitud.

En los sistemas de división de frente de onda, la onda se divide en el espacio; por ejemplo, el interferómetro de doble rendija de Young y el espejo de Lloyd.

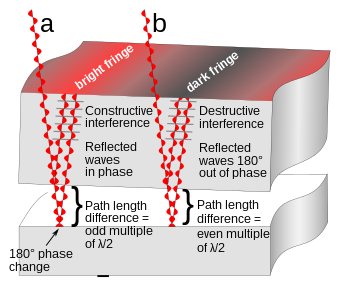
La interferencia también se puede ver en fenómenos cotidianos como la iridiscencia y la coloración estructural. Por ejemplo, los colores que se ven en una pompa de jabón surgen de la interferencia de la luz que se refleja en las superficies delantera y trasera de la fina película de jabón. Dependiendo del grosor de la película, los diferentes colores interfieren de manera constructiva y destructiva.

Aplicaciones

Golpe

En acústica, un tiempo es un patrón de interferencia entre dos sonidos de frecuencias ligeramente diferentes, percibido como una variación periódica de volumen cuya tasa es la diferencia de las dos frecuencias.

Con instrumentos de afinación que pueden producir tonos sostenidos, los tiempos se pueden reconocer fácilmente. Afinar dos tonos al unísono presentará un efecto peculiar: cuando los dos tonos tienen un tono similar pero no son idénticos, la diferencia de frecuencia genera la pulsación. El volumen varía como en un trémolo a medida que los sonidos interfieren alternativamente de manera constructiva y destructiva. A medida que los dos tonos se acercan gradualmente al unísono, el latido se ralentiza y puede volverse tan lento que sea imperceptible. A medida que los dos tonos se separan más, su frecuencia de pulsación comienza a acercarse al rango de la percepción tonal humana, la pulsación empieza a sonar como una nota y se produce un tono combinado. Este tono de combinación también se puede denominar fundamental faltante, ya que la frecuencia de pulsación de dos tonos cualesquiera es equivalente a la frecuencia de su frecuencia fundamental implícita.

Interferometría óptica

La interferometría ha jugado un papel importante en el avance de la física y también tiene una amplia gama de aplicaciones en la medición física y de ingeniería.

El interferómetro de doble rendija de Thomas Young de 1803 demostró franjas de interferencia cuando dos pequeños orificios se iluminaban con la luz de otro pequeño orificio iluminado por la luz solar. Young pudo estimar la longitud de onda de diferentes colores en el espectro a partir del espaciado de las franjas. El experimento jugó un papel importante en la aceptación general de la teoría ondulatoria de la luz. En mecánica cuántica, se considera que este experimento demuestra la inseparabilidad de las naturalezas de onda y partícula de la luz y otras partículas cuánticas (dualidad onda-partícula). A Richard Feynman le gustaba decir que toda la mecánica cuántica se puede deducir pensando detenidamente en las implicaciones de este único experimento.

Los resultados del experimento de Michelson-Morley generalmente se consideran la primera evidencia fuerte en contra de la teoría de un éter luminífero y a favor de la relatividad especial.

La interferometría se ha utilizado para definir y calibrar estándares de longitud. Cuando el metro se definió como la distancia entre dos marcas en una barra de platino-iridio, Michelson y Benoît usaron interferometría para medir la longitud de onda de la línea roja de cadmio en el nuevo estándar y también demostraron que podría usarse como un estándar de longitud. Sesenta años después, en 1960, el metro en el nuevo sistema SI se definió como igual a 1.650.763,73 longitudes de onda de la línea de emisión naranja-roja en el espectro electromagnético del átomo de criptón-86 en el vacío. Esta definición fue reemplazada en 1983 por la definición del metro como la distancia recorrida por la luz en el vacío durante un intervalo de tiempo específico. La interferometría sigue siendo fundamental para establecer la cadena de calibración en la medición de longitud.

La interferometría se usa en la calibración de medidores de deslizamiento (llamados bloques patrón en los EE. UU.) y en máquinas de medición por coordenadas. También se utiliza en la prueba de componentes ópticos.

Radiointerferometría

El Array Muy Grande, un array interferométrico formado por muchos telescopios más pequeños, como muchos telescopios de radio más grandes.

En 1946, se desarrolló una técnica llamada interferometría astronómica. Los interferómetros de radio astronómicos generalmente consisten en conjuntos de platos parabólicos o conjuntos bidimensionales de antenas omnidireccionales. Todos los telescopios del conjunto están ampliamente separados y, por lo general, están conectados entre sí mediante un cable coaxial, una guía de ondas, fibra óptica u otro tipo de línea de transmisión. La interferometría aumenta la señal total recopilada, pero su objetivo principal es aumentar enormemente la resolución a través de un proceso llamado síntesis de apertura. Esta técnica funciona superponiendo (interfiriendo) las ondas de señal de los diferentes telescopios bajo el principio de que las ondas que coinciden con la misma fase se sumarán entre sí, mientras que dos ondas que tengan fases opuestas se anularán entre sí. Esto crea un telescopio combinado que es equivalente en resolución (aunque no en sensibilidad) a una sola antena cuyo diámetro es igual al espaciado de las antenas más alejadas del conjunto.

Interferometría acústica

Un interferómetro acústico es un instrumento para medir las características físicas de las ondas sonoras en un gas o líquido, como velocidad, longitud de onda, absorción o impedancia. Un cristal vibrante crea ondas ultrasónicas que se irradian al medio. Las ondas golpean un reflector colocado paralelo al cristal, se reflejan de vuelta a la fuente y se miden.

Interferencia cuántica

La interferencia cuántica es bastante diferente de la interferencia de onda clásica descrita anteriormente. A continuación, se proporciona una enumeración de las diferencias importantes. Sin embargo, la interferencia cuántica es similar a la interferencia óptica.

Vamos Ψ Ψ ()x,t){displaystyle Psi (x,t)} ser una solución de funcionamiento de onda de la ecuación Schrödinger para un objeto mecánico cuántico. Entonces la probabilidad P()x){displaystyle P(x)} de observar el objeto en posición x{displaystyle x} es P()x)=SilencioΨ Ψ ()x,t)Silencio2=Ψ Ψ Alternativa Alternativa ()x,t)Ψ Ψ ()x,t){displaystyle P(x)= ToddPsi (x,t) donde * indica conjugación compleja. La interferencia cuántica se refiere a la cuestión de esta probabilidad cuando la función de onda se expresa como una suma o superposición lineal de dos términos Ψ Ψ ()x,t)=Ψ Ψ A()x,t)+Ψ Ψ B()x,t){displaystyle Psi (x,t)=Psi _{A}(x,t)+Psi _{B}(x,t)}:

P()x)=SilencioΨ Ψ ()x,t)Silencio2=SilencioΨ Ψ A()x,t)Silencio2+SilencioΨ Ψ B()x,t)Silencio2+()Ψ Ψ AAlternativa Alternativa ()x,t)Ψ Ψ B()x,t)+Ψ Ψ A()x,t)Ψ Ψ BAlternativa Alternativa ()x,t)){displaystyle P(x)=perseverPsi (x,t) sometida^{2}= arrestPsi _{A}(x,t) Previous^{2}Psi _{B}(x,t) Psi _{A}^{*}(x,t)Psi _{B}(x,t)+Psi _{A}(x,t)Psi _{B}^{*}(x,t)}

Normalmente, Ψ Ψ A()x,t){displaystyle Psi _{A}(x,t)} y Ψ Ψ B()x,t){displaystyle Psi _{B}(x,t)} corresponden a situaciones distintas A y B. Cuando este es el caso, la ecuación Ψ Ψ ()x,t)=Ψ Ψ A()x,t)+Ψ Ψ B()x,t){displaystyle Psi (x,t)=Psi _{A}(x,t)+Psi _{B}(x,t)} indica que el objeto puede estar en situación A o situación B. La ecuación anterior puede ser interpretada como: La probabilidad de encontrar el objeto en x{displaystyle x} es la probabilidad de encontrar el objeto en x{displaystyle x} cuando está en situación A más la probabilidad de encontrar el objeto en x{displaystyle x} cuando está en situación B más un término extra. Este término extra, que se llama quantum interference term, es Ψ Ψ AAlternativa Alternativa ()x,t)Ψ Ψ B()x,t)+Ψ Ψ A()x,t)Ψ Ψ BAlternativa Alternativa ()x,t){displaystyle Psi _{*}(x,t)Psi _{B}(x,t)+Psi _{A}(x,t)Psi _{B}{*}(x,t)} en la ecuación anterior. Como en el caso de onda clásica anterior, el término de interferencia cuántica puede agregar (intromisión constructiva) o subtracto (intromisión destructiva) de SilencioΨ Ψ A()x,t)Silencio2+SilencioΨ Ψ B()x,t)Silencio2{displaystyle SilencioPsi _{A}(x,t) sometida^{2}+ sometidaPsi _{B}(x,t) en la ecuación anterior dependiendo de si el término de interferencia cuántica es positivo o negativo. Si este término está ausente para todos x{displaystyle x}, entonces no hay interferencia mecánica cuántica asociada con situaciones A y B.

El ejemplo más conocido de interferencia cuántica es el experimento de doble impacto. En este experimento, electrones, átomos u otros objetos mecánicos cuánticos se acercan a una barrera con dos aberturas en ella. Si el objeto cuántico logra pasar por las aberturas, su posición se mide con una pantalla de detección a cierta distancia más allá y detrás de la barrera. Para este sistema, se permite Ψ Ψ A()x,t){displaystyle Psi _{A}(x,t)} ser esa parte de la función de onda que pasa a través de una de las aberturas y permite Ψ Ψ B()x,t){displaystyle Psi _{B}(x,t)} ser esa parte de la función de onda que pasa por la otra abertura. Cuando el objeto casi llega a la pantalla, la probabilidad de donde se encuentra se da por la ecuación anterior. En este contexto, la ecuación dice que la probabilidad de encontrar el objeto en algún momento justo antes de que golpee la pantalla es la probabilidad que se obtenería si pasara por la primera hendidura más la probabilidad que se conseguiría si pasara por la segunda hendidura más el término de interferencia cuántica, que no tiene contraparte en la física clásica. El término de interferencia cuántica puede cambiar significativamente el patrón observado en la pantalla de detección.

La separación del servicio Ψ Ψ A()x,t)+Ψ Ψ B()x,t){displaystyle Psi _{A}(x,t)+Psi _{B}(x,t)} es particularmente claro en el camino la formulación integral de la mecánica cuántica en el contexto del experimento de doble impacto. Ψ Ψ A()x,t){displaystyle Psi _{A}(x,t)} consiste en el camino de las contribuciones integrales en las que los caminos pasan por la primera abertura; Ψ Ψ B()x,t){displaystyle Psi _{B}(x,t)} consiste en la ruta de las contribuciones integrales en las que pasan por la segunda abertura.

Aquí hay una lista de algunas de las diferencias entre la interferencia de onda clásica y la interferencia cuántica:

1. En la interferencia clásica, dos ondas diferentes interfieren; En la interferencia cuántica, la función de onda interfiere consigo misma.
2. La interferencia clásica se obtiene simplemente añadiendo los desplazamientos del equilibrio (o amplitudes) de las dos ondas; En la interferencia cuántica, el efecto ocurre para la función de probabilidad asociada con la función de onda y por lo tanto el módulo de la función de onda cuadrado.
3. La interferencia implica diferentes tipos de funciones matemáticas: Una onda clásica es una función real que representa el desplazamiento de una posición de equilibrio; una función de onda cuántica es una función compleja. Una onda clásica en cualquier punto puede ser positiva o negativa; la función de probabilidad cuántica es no negativa.
4. En la interferencia óptica clásica se viola el principio de conservación de la energía ya que requiere quanta para cancelar. En la conservación de la energía de interferencia cuántica no se viola, el quanta simplemente asume caminos por el camino integral. Todo quanta por ejemplo termina en áreas brillantes del patrón.