Intercambio de llaves Diffie-Hellman

El intercambio de claves Diffie-Hellman es un método matemático de intercambio seguro de claves criptográficas a través de un canal público y fue uno de los primeros protocolos de clave pública tal como lo concibió Ralph Merkle y recibió su nombre de Whitfield Diffie y Martin. Demonios, hombre. DH es uno de los primeros ejemplos prácticos de intercambio de clave pública implementado en el campo de la criptografía. Publicado en 1976 por Diffie y Hellman, este es el primer trabajo conocido públicamente que propuso la idea de una clave privada y una clave pública correspondiente.

Tradicionalmente, la comunicación cifrada segura entre dos partes requería que primero intercambiaran claves por algún medio físico seguro, como listas de claves en papel transportadas por un servicio de mensajería de confianza. El método de intercambio de claves Diffie-Hellman permite que dos partes que no se conocen previamente establezcan conjuntamente una clave secreta compartida a través de un canal no seguro. Esta clave se puede usar para cifrar comunicaciones posteriores mediante un cifrado de clave simétrica.

Diffie–Hellman se utiliza para asegurar una variedad de servicios de Internet. Sin embargo, una investigación publicada en octubre de 2015 sugiere que los parámetros en uso para muchas aplicaciones de Internet DH en ese momento no son lo suficientemente fuertes como para evitar el compromiso de atacantes muy bien financiados, como los servicios de seguridad de algunos países.

El esquema fue publicado por Whitfield Diffie y Martin Hellman en 1976, pero en 1997 se reveló que James H. Ellis, Clifford Cocks y Malcolm J. Williamson de GCHQ, la agencia de inteligencia de señales británica, habían mostrado previamente en 1969 cómo se podría lograr la criptografía de clave pública.

Aunque el acuerdo de clave Diffie-Hellman en sí mismo es un protocolo de acuerdo de clave no autenticado, proporciona la base para una variedad de protocolos autenticados y se utiliza para brindar confidencialidad directa en los modos efímeros de Transport Layer Security (referidos como EDH o DHE según el conjunto de cifrado).

El método fue seguido poco después por RSA, una implementación de criptografía de clave pública que utiliza algoritmos asimétricos.

Vencido EE. UU. La patente 4.200.770 de 1977 describe el algoritmo ahora de dominio público. Acredita a Hellman, Diffie y Merkle como inventores.

Nombre

En 2002, Hellman sugirió que el algoritmo se llamara intercambio de claves Diffie-Hellman-Merkle en reconocimiento a la contribución de Ralph Merkle a la invención de la criptografía de clave pública (Hellman, 2002), escritura:

El sistema... se ha conocido desde entonces como intercambio clave Diffie-Hellman. Mientras que ese sistema fue descrito por primera vez en un papel por Diffie y yo, es un sistema de distribución de claves públicas, un concepto desarrollado por Merkle, y por lo tanto debe llamarse "Intercambio clave Diffie-Hellman-Merkle" si los nombres van a estar asociados con él. Espero que este pequeño púlpito pueda ayudar en ese esfuerzo de reconocer la contribución igual de Merkle a la invención de la criptografía de clave pública.

Descripción

Visión general

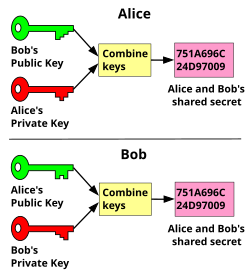
El intercambio de claves Diffie-Hellman establece un secreto compartido entre dos partes que se puede usar para comunicaciones secretas para intercambiar datos a través de una red pública. Una analogía ilustra el concepto de intercambio de clave pública mediante el uso de colores en lugar de números muy grandes:

El proceso comienza cuando las dos partes, Alice y Bob, acuerdan públicamente un color inicial arbitrario que no es necesario mantener en secreto. En este ejemplo, el color es amarillo. Cada persona también selecciona un color secreto que guardan para sí mismos, en este caso, rojo y cian. La parte crucial del proceso es que Alice y Bob mezclen cada uno su propio color secreto junto con el color que comparten mutuamente, lo que da como resultado mezclas de naranja-tostado y azul claro respectivamente, y luego intercambian públicamente los dos colores mezclados. Finalmente, cada uno de ellos mezcla el color que recibió de la pareja con su propio color privado. El resultado es una mezcla de color final (amarillo-marrón en este caso) que es idéntica a la mezcla de color final de su pareja.

Si un tercero escuchara el intercambio, solo conocería el color común (amarillo) y los primeros colores mezclados (naranja-tostado y azul claro), pero sería muy difícil para ellos descubrir el final. color secreto (amarillo-marrón). Llevando la analogía a un intercambio de la vida real utilizando grandes números en lugar de colores, esta determinación es computacionalmente costosa. Es imposible calcular en una cantidad práctica de tiempo incluso para las supercomputadoras modernas.

Explicación criptográfica

La implementación más simple y original del protocolo utiliza el grupo multiplicativo de enteros módulo p, donde p es primo y g es una raíz primitiva módulo p. Estos dos valores se eligen de esta manera para garantizar que el secreto compartido resultante pueda tomar cualquier valor de 1 a p–1. Este es un ejemplo del protocolo, con valores no secretos en azul y valores secretos en rojo.

1. Alice y Bob aceptan públicamente usar un módulo p = 23 y base g = 5 (que es un modulo de raíz primitivo 23).
2. Alice elige un entero secreto a = 4, entonces envía Bob A = g^a mod p
   • A = 5⁴ mod 23 = 4 (en este ejemplo ambos A y a tienen el mismo valor 4, pero esto generalmente no es el caso)
3. Bob elige un entero secreto b = 3, entonces envía Alice B = g^b mod p
   • B = 5³ mod 23 = 10
4. Alice computes s = B^a mod p
   • s = 10⁴ mod 23 = 18
5. Bob computes s = A^b mod p
   • s = 4³ mod 23 = 18
6. Alice y Bob ahora comparten un secreto (el número 18).

Tanto Alice como Bob han llegado a los mismos valores porque bajo mod p,

Abmodp=gabmodp=gbamodp=Bamodp{displaystyle {color {fnK}A}{color} {Red}b}{bmod {color {Blue}p}={color {Blue}g}{color}p}p} {color}p}p}p}= {color}g}g} {c}p}p}p} {cccH}p}p}p}p}p}pccccH0}p}p}p}p}p}p}pccccccccccccccccccccccccccccccccccccccccccccccccccccc}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p {Red}ab}{bmod {color {Blue}p}={color {Blue}g}{color}p}p} {color}p}p}= {cH0}p}p} {cH0}p} {cH0}p}cH0}} {cH00}}}ccH00}}}}}}}} {c}}}}}}}}}}} {ccccccccccccccccccccccccccccccccccccccccccccccccccccccH0ccccccccccccccH {Red}ba}{bmod {color {Blue}p}={color} {Blue}B}{color} {Red}a}{bmod {color} {Blue}p}}

Más específicamente,

()gamodp)bmodp=()gbmodp)amodp{displaystyle ({color {Blue}g}{color {Red}a}{bmod {color} {Blue}p}} {color} {Red}b}{bmod {color} {Blue}p}= {color {Blue}g}{color {Red}b}{bmod {bmod {color}g} {cHFF}g} {cHFF} {cHFF}p}p}p}p}p}p}= {cccccH00}pccH0}p}pcccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccHFF}p}pccccccccHFF}p}pcH {Blue}p}} {color} {Red}a}{bmod {color} {Blue}p}}

Solo a y b se mantienen en secreto. Todos los demás valores: p, g, g^a mod p y g^b mod p – se envían en claro. La fuerza del esquema proviene del hecho de que g^ab mod p = g^ba mod p tarda mucho tiempo en calcularse mediante cualquier algoritmo conocido solo a partir del conocimiento de p, g, g^a mod p, y g^b mod p. Una vez que Alice y Bob calculan el secreto compartido, pueden usarlo como una clave de cifrado, conocida solo por ellos, para enviar mensajes a través del mismo canal de comunicación abierto.

Por supuesto, se necesitarían valores mucho mayores de a, b y p para que este ejemplo sea seguro, ya que solo hay 23 resultados posibles de n mod 23. Sin embargo, si p es un número primo de al menos 600 dígitos, incluso las computadoras modernas más rápidas que usan el algoritmo conocido más rápido no pueden encontrar a dado solo g, p y g^a mod p. Tal problema se llama el problema del logaritmo discreto. El cálculo de g^a mod p se conoce como exponenciación modular y se puede realizar de manera eficiente incluso para números grandes. Tenga en cuenta que g no necesita ser grande en absoluto, y en la práctica suele ser un número entero pequeño (como 2, 3,...).

Cuadro de secretos

El siguiente gráfico muestra quién sabe qué, de nuevo con valores no secretos en azul y valores secretos en rojo. Aquí, Eve es una espía: observa lo que se envía entre Alice y Bob, pero no altera el contenido de sus comunicaciones.

• g = base pública (raíz primitiva), conocida por Alice, Bob y Eva. g = 5
• p = módulo público (prime), conocido por Alice, Bob y Eva. p = 23
• a = La llave privada de Alice, conocida sólo por Alice. a = 6
• b = La llave privada de Bob sólo conocida por Bob. b = 15
• A = La llave pública de Alice, conocida por Alice, Bob y Eve. A = g^a mod p = 8
• B = La llave pública de Bob, conocida por Alice, Bob y Eve. B = g^b mod p = 19

Alice Conocido Desconocida p = 23 g = 5 a = 6 b A = 5a mod 23 A = 56 mod 23 = 8 B = 19 s = Ba mod 23 s = 196 mod 23 = 2

Bob Conocido Desconocida p = 23 g = 5 b = 15 a B = 5b mod 23 B = 515 mod 23 = 19 A = 8 s = Ab mod 23 s = 815 mod 23 = 2

Eve Conocido Desconocida p = 23 g = 5 a, b A = 8, B = 19 s

Ahora s es la clave secreta compartida y Alice y Bob la conocen, pero no a Eva. Tenga en cuenta que no es útil para Eve calcular AB, que es igual a g^{a + b} mod p.

Nota: Debería ser difícil para Alice resolver la clave privada de Bob o para Bob resolver la clave privada de Alice. Si no es difícil para Alice encontrar la clave privada de Bob (o viceversa), Eve puede simplemente sustituir su propio par de claves pública/privada, conectar la clave pública de Bob en su clave privada, producir un falsificar la clave secreta compartida y resolver la clave privada de Bob (y usarla para resolver la clave secreta compartida. Eve puede intentar elegir un par de claves públicas/privadas que le faciliten la resolución de Bob' 39;s clave privada).

Generalización a grupos cíclicos finitos

Aquí hay una descripción más general del protocolo:

1. Alice y Bob están de acuerdo en un grupo cíclico finito G de orden n y un elemento generador g dentro G. (Esto generalmente se hace mucho antes del resto del protocolo; g se supone que son conocidos por todos los atacantes.) El grupo G está escrito multiplicativamente.
2. Alice elige un número natural aleatorio a con 1 a. n, y envía el elemento g^a de G a Bob.
3. Bob elige un número natural aleatorio b con 1 b. n, y envía el elemento g^b de G a Alice.
4. Alice compute el elemento (g^b)^a = g^ba de G.
5. Bob compute el elemento (g^a)^b = g^ab de G.

Alice y Bob ahora están en posesión del elemento de grupo g^ab = g^ba, que puede servir como clave secreta compartida. El grupo G satisface la condición requerida para una comunicación segura siempre que no exista un algoritmo eficiente para determinar g^ab dado g, g^a y g^b.

Por ejemplo, el protocolo Diffie-Hellman de curva elíptica es una variante que representa un elemento de G como un punto en una curva elíptica en lugar de un módulo entero n. También se han propuesto variantes que utilizan curvas hiperelípticas. El intercambio de claves de isogenia supersingular es una variante de Diffie-Hellman que ha sido diseñada para ser segura contra las computadoras cuánticas.

Teclas Efímeras y/o Estáticas

Las claves utilizadas pueden ser claves efímeras o estáticas (a largo plazo), pero incluso pueden ser mixtas, lo que se denomina DH semiestático. Estas variantes tienen diferentes propiedades y, por lo tanto, diferentes casos de uso. Se puede encontrar una descripción general de muchas variantes y algunas discusiones, por ejemplo, en NIST SP 800-56A. Aquí solo una lista básica:

1. efímero, efímero: Usualmente se utiliza para un acuerdo clave. Provee el secreto, pero no la autenticidad.
2. estática, estática: Generaría un secreto compartido a largo plazo. No proporciona el secreto adelante, pero la autenticidad implícita. Como las llaves están estáticas, por ejemplo, no protegería contra los ataques de repetición.
3. efímero, estático: Por ejemplo utilizado en el sistema de encriptación ElGamal o en el esquema de cifrado integrado (IES). Si se utiliza en un acuerdo clave podría proporcionar autenticidad unilateral implícita (el lado efímero podría verificar la autenticidad del lado estático). No se proporciona ningún secreto.

Es posible usar claves efímeras y estáticas en un acuerdo clave para brindar más seguridad, como se muestra, por ejemplo, en NIST SP 800-56A, pero también es posible combinarlas en un solo intercambio de claves DH, que luego se denomina triple DH (3-DH).

Triple Diffie-Hellman (3-DH)

En 1997, Simon Blake-Wilson, Don Johnson, Alfred Menezes propusieron una especie de triple DH en "Key Agreement Protocols and their Security Analysis (1997)", que fue mejorado por C. Kudla y K. G. Paterson en "Modular Security Proofs for Key Agreement Protocols (2005)" y se demostró que es seguro. También se usa o se menciona en otras variantes. Por ejemplo:

• Extended Triple Diffie-Hellman
• sci.crypt news group (de 18.08.2002)
• Algorit de doble Ratchet
• Protocolo de firma

Las claves secretas a largo plazo de Alice y Bob se indican con a y b respectivamente, con claves públicas A y B , así como los pares de claves efímeras x, X y y, Y. Entonces el protocolo es:

Protocolo Triple Diffie-Hellman (3-DH)

Alice.A=ga{displaystyle A=g^{a})		Bob.B=gb{displaystyle B=g^{b})
X=gx{displaystyle X=g^{x}	X⇒ ⇒ {displaystyle XRightarrow }
	Alternativa Alternativa Y{displaystyle "Leftarrow Y"	Y=gSí.{displaystyle Y=g^{y}
K=KDF()Yx,Bx,Ya,X,Y,A,B){displaystyle K=KDF(Y^{x},B^{x},Y^{a},X,Y,A,B)}		K=KDF()XSí.,Xb,ASí.,X,Y,A,B){displaystyle K=KDF(X^{y},X^{b},A^{y},X,Y,A,B)}

Las claves públicas a largo plazo deben transferirse de alguna manera. Eso se puede hacer de antemano en un canal de confianza separado, o las claves públicas se pueden cifrar mediante algún acuerdo de clave parcial para preservar el anonimato. Para obtener más detalles de este tipo, así como otras mejoras, como la protección del canal lateral o la confirmación de clave explícita, así como los primeros mensajes y la autenticación de contraseña adicional, se podría, por ejemplo. eche un vistazo a "Apretón de manos modular avanzado para acuerdo de clave y autenticación opcional"

Operación con más de dos partes

El acuerdo de clave Diffie-Hellman no se limita a negociar una clave compartida por solo dos participantes. Cualquier número de usuarios puede participar en un acuerdo realizando iteraciones del protocolo del acuerdo e intercambiando datos intermedios (que no necesitan mantenerse en secreto). Por ejemplo, Alice, Bob y Carol podrían participar en un acuerdo Diffie-Hellman de la siguiente manera, tomando todas las operaciones como módulo p:

1. Las partes están de acuerdo en los parámetros del algoritmo p y g.
2. Las partes generan sus llaves privadas, llamadas a, b, y c.
3. Alice computes g^a mod p y se lo envía a Bob.
4. Bob computes ()g^a)^b mod p = g^ab mod p y lo envía a Carol.
5. Carol computes ()g^ab)^c mod p = g^abc mod p y lo usa como su secreto.
6. Bob computes g^b mod p y lo envía a Carol.
7. Carol computes ()g^b)^c mod p = g^bc mod p y lo envía a Alice.
8. Alice computes ()g^bc)^a mod p = g^bca mod p = g^abc mod p y lo usa como su secreto.
9. Carol computes g^c mod p y lo envía a Alice.
10. Alice computes ()g^c)^a mod p = g^ca mod p y se lo envía a Bob.
11. Bob computes ()g^ca)^b mod p = g^taxi mod p = g^abc mod p y lo usa como su secreto.

Un espía ha podido ver g^a mod p, g^b mod p, g^c mod p, g^ab mod p, g^ac mod p y g^bc mod p, pero no puede usar ninguna combinación de estos para reproducir eficientemente g^abc mod p.

Para extender este mecanismo a grupos más grandes, se deben seguir dos principios básicos:

• Comenzando con una tecla "vacío" que consiste sólo en g, el secreto se hace al elevar el valor actual al exponente privado de cada participante una vez, en cualquier orden (la primera de tales exponentes produce la propia clave pública del participante).
• Cualquier valor intermedio (tener hasta N-1 exponentes aplicados, donde N es el número de participantes en el grupo) puede ser revelado públicamente, pero el valor final (habiendo tenido todo N exponentes aplicados) constituye el secreto compartido y por lo tanto nunca debe ser revelado públicamente. Así, cada usuario debe obtener su copia del secreto mediante la aplicación de su propia clave privada última (otra vez no habría manera de que el último contribuyente comunicara la clave final a su destinatario, ya que el último contribuyente habría convertido la clave en el mismo secreto que el grupo deseaba proteger).

Estos principios dejan abiertas varias opciones para elegir en qué orden los participantes contribuyen a las claves. La solución más simple y obvia es colocar a los N participantes en un círculo y hacer que las N llaves giren alrededor del círculo, hasta que finalmente todas las llaves hayan sido aportadas por todos los N participantes (terminando con su dueño) y cada participante ha contribuido a N claves (terminando con la propia). Sin embargo, esto requiere que cada participante realice N exponenciaciones modulares.

Al elegir un orden más óptimo y confiar en el hecho de que las claves se pueden duplicar, es posible reducir el número de exponenciaciones modulares realizadas por cada participante a log₂(N) + 1 usando un enfoque de estilo divide y vencerás, dado aquí para ocho participantes:

1. Los participantes A, B, C y D realizan cada una una de las exponencias, rindiendo g^abcd; este valor se envía a E, F, G y H. A cambio, los participantes A, B, C y D reciben g^efgh.
2. Participantes A y B cada uno realiza una exponenciación, dando lugar g^efghab, que envían a C y D, mientras que C y D hacen lo mismo, rindiendo g^efghcd, que envían a A y B.
3. Participante A realiza una exponenciación, rindiendo g^efghcda, que envía a B; similarmente, B envía g^efghcdb A. C y D hacen lo mismo.
4. Participante Una realiza una exponenciación final, dando el secreto g^efghcdba = g^abcdefgh, mientras B hace lo mismo para conseguir g^efghcdab = g^abcdefgh; de nuevo, C y D hacen lo mismo.
5. Participantes E a través de H realiza simultáneamente las mismas operaciones g^abcd como punto de partida.

Una vez que se haya completado esta operación, todos los participantes poseerán el secreto g^abcdefgh, pero cada participante habrá realizado solo cuatro exponenciaciones modulares, en lugar de las ocho implicadas por un disposición circular sencilla.

Seguridad

El protocolo se considera seguro contra los espías si G y g se eligen correctamente. En particular, el orden del grupo G debe ser grande, particularmente si el mismo grupo se usa para grandes cantidades de tráfico. El intruso tiene que resolver el problema de Diffie-Hellman para obtener g^ab. Actualmente, esto se considera difícil para grupos cuyo pedido es lo suficientemente grande. Un algoritmo eficiente para resolver el problema del logaritmo discreto facilitaría el cálculo de a o b y resolvería el problema de Diffie-Hellman, haciendo que este y muchos otros criptosistemas de clave pública sean inseguros. Los campos de características pequeñas pueden ser menos seguros.

El orden de G debe tener un factor primo grande para evitar el uso del algoritmo de Pohlig-Hellman para obtener a o b. Por esta razón, a veces se usa un número primo de Sophie Germain q para calcular p = 2q + 1, llamado primo seguro, ya que el orden de G solo es divisible por 2 y q. A veces se elige g para generar el subgrupo de orden q de G, en lugar de G, de modo que Legendre El símbolo de g^a nunca revela el bit de orden inferior de a. Un protocolo que usa tal elección es, por ejemplo, IKEv2.

g suele ser un número entero pequeño como 2. Debido a la autorreducibilidad aleatoria del problema del logaritmo discreto, un pequeño g es igualmente seguro que cualquier otro generador de el mismo grupo

Si Alice y Bob usan generadores de números aleatorios cuyas salidas no son completamente aleatorias y pueden predecirse hasta cierto punto, entonces es mucho más fácil escuchar a escondidas.

En la descripción original, el intercambio Diffie-Hellman por sí solo no proporciona la autenticación de las partes que se comunican y, por lo tanto, es vulnerable a un ataque de intermediario. Mallory (un atacante activo que ejecuta el ataque man-in-the-middle) puede establecer dos intercambios de claves distintos, uno con Alice y el otro con Bob, haciéndose pasar efectivamente por Alice para Bob, y viceversa, lo que le permite descifrar y luego recuperar. -cifrar, los mensajes que se pasan entre ellos. Tenga en cuenta que Mallory debe seguir estando en el medio, descifrando y volviendo a cifrar activamente los mensajes cada vez que Alice y Bob se comunican. Si alguna vez está ausente, su presencia anterior se revela a Alice y Bob. Sabrán que todas sus conversaciones privadas fueron interceptadas y decodificadas por alguien en el canal. En la mayoría de los casos, no les ayudará a obtener la clave privada de Mallory, incluso si utilizó la misma clave para ambos intercambios.

Por lo general, se necesita un método para autenticar a las partes que se comunican entre sí para evitar este tipo de ataque. En su lugar, se pueden usar variantes de Diffie-Hellman, como el protocolo STS, para evitar este tipo de ataques.

Prácticos ataques al tráfico de Internet

El algoritmo tamiz de campos numéricos, que generalmente es el más efectivo para resolver el problema del logaritmo discreto, consta de cuatro pasos computacionales. Los primeros tres pasos solo dependen del orden del grupo G, no del número específico cuyo logaritmo finito se desea. Resulta que gran parte del tráfico de Internet utiliza uno de los pocos grupos que son del orden de 1024 bits o menos. Al calcular previamente los primeros tres pasos del tamiz de campo numérico para los grupos más comunes, un atacante solo necesita llevar a cabo el último paso, que es mucho menos costoso computacionalmente que los primeros tres pasos, para obtener un logaritmo específico. El ataque Logjam usó esta vulnerabilidad para comprometer una variedad de servicios de Internet que permitieron el uso de grupos cuyo orden era un número primo de 512 bits, denominado grado de exportación. Los autores necesitaron varios miles de núcleos de CPU durante una semana para calcular previamente los datos de un solo número primo de 512 bits. Una vez hecho esto, los logaritmos individuales podrían resolverse en aproximadamente un minuto utilizando dos CPU Intel Xeon de 18 núcleos.

Según lo estimado por los autores detrás del ataque Logjam, el precálculo mucho más difícil necesario para resolver el problema del registro discreto para un número primo de 1024 bits costaría alrededor de $ 100 millones, muy dentro del presupuesto de una gran agencia de inteligencia nacional. como la Agencia de Seguridad Nacional de los Estados Unidos (NSA). Los autores de Logjam especulan que el precálculo contra primos DH de 1024 bits ampliamente reutilizados está detrás de las afirmaciones en documentos filtrados de la NSA de que la NSA es capaz de romper gran parte de la criptografía actual.

Para evitar estas vulnerabilidades, los autores de Logjam recomiendan el uso de criptografía de curva elíptica, para la cual no se conoce ningún ataque similar. De lo contrario, recomiendan que el orden, p, del grupo Diffie-Hellman sea de al menos 2048 bits. Calculan que el cálculo previo requerido para un número primo de 2048 bits es 10⁹ veces más difícil que para números primos de 1024 bits.

Otros usos

Cifrado

Se han propuesto esquemas de cifrado de clave pública basados en el intercambio de claves Diffie-Hellman. El primer esquema de este tipo es el cifrado ElGamal. Una variante más moderna es el Esquema de cifrado integrado.

Secreto hacia adelante

Los protocolos que logran el secreto directo generan nuevos pares de claves para cada sesión y los descartan al final de la sesión. El intercambio de claves Diffie-Hellman es una opción frecuente para dichos protocolos, debido a su rápida generación de claves.

Acuerdo de clave autenticada con contraseña

Cuando Alice y Bob comparten una contraseña, pueden usar una forma de acuerdo de clave autenticada (PK) de contraseña de Diffie-Hellman para evitar ataques de intermediarios. Un esquema simple es comparar el hash de s concatenados con la contraseña calculada independientemente en ambos extremos del canal. Una característica de estos esquemas es que un atacante solo puede probar una contraseña específica en cada iteración con la otra parte, por lo que el sistema proporciona una buena seguridad con contraseñas relativamente débiles. Este enfoque se describe en la Recomendación ITU-T X.1035, que es utilizada por el estándar de redes domésticas G.hn.

Un ejemplo de dicho protocolo es el protocolo de contraseña remota segura.

Clave pública

También es posible utilizar Diffie-Hellman como parte de una infraestructura de clave pública, permitiendo a Bob cifrar un mensaje para que sólo Alice pueda descifrarlo, sin comunicación previa entre ellos aparte de Bob teniendo conocimiento confiable de la clave pública de Alice. La clave pública de Alice es ()gamodp,g,p){displaystyle (g^{a}{bmod {p},g,p)}. Para enviarle un mensaje, Bob elige un azar b y luego envía Alice gbmodp{displaystyle g^{b}{bmod {p}} (sin cifrar) junto con el mensaje encriptado con clave simétrica ()ga)bmodp{fnK}. Sólo Alice puede determinar la clave simétrica y por lo tanto descifrar el mensaje porque sólo ella tiene a (la clave privada). Una llave pública pre-compartida también impide los ataques entre hombres y medio.

En la práctica, Diffie–Hellman no se usa de esta manera, siendo RSA el algoritmo de clave pública dominante. Esto se debe principalmente a razones históricas y comerciales, a saber, que RSA Security creó una autoridad de certificación para la firma de claves que se convirtió en Verisign. Diffie-Hellman, como se explicó anteriormente, no se puede usar directamente para firmar certificados. Sin embargo, los algoritmos de firma ElGamal y DSA están relacionados matemáticamente con él, así como MQV, STS y el componente IKE del conjunto de protocolos IPsec para proteger las comunicaciones del Protocolo de Internet.