Interacción electrodébil

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Descripción unificada del electromagnetismo y la interacción débil

En física de partículas, la interacción electrodébil o fuerza electrodébil es la descripción unificada de dos de las cuatro interacciones fundamentales conocidas de la naturaleza: el electromagnetismo y la interacción débil. Aunque estas dos fuerzas parecen muy diferentes a bajas energías todos los días, la teoría las modela como dos aspectos diferentes de la misma fuerza. Por encima de la energía de unificación, del orden de 246 GeV, se fusionarían en una sola fuerza. Por lo tanto, si la temperatura es lo suficientemente alta, aproximadamente 10¹⁵ K, entonces la fuerza electromagnética y la fuerza débil se fusionan en una fuerza electrodébil combinada. Durante la época de los quarks (poco después del Big Bang), la fuerza electrodébil se dividió en fuerza electromagnética y fuerza débil. Se cree que la temperatura requerida de 10¹⁵ K no se ha visto ampliamente en todo el universo desde antes de la época de los quarks, y actualmente la temperatura más alta creada por el hombre en equilibrio térmico es de alrededor de 5,5x10¹² K (del Gran Colisionador de Hadrones).

Sheldon Glashow, Abdus Salam y Steven Weinberg recibieron el Premio Nobel de Física de 1979 por sus contribuciones a la unificación de la interacción débil y electromagnética entre partículas elementales, conocida como la teoría de Weinberg-Salam. La existencia de interacciones electrodébiles se estableció experimentalmente en dos etapas, la primera fue el descubrimiento de corrientes neutras en la dispersión de neutrinos por la colaboración Gargamelle en 1973, y la segunda en 1983 por las colaboraciones UA1 y UA2 que involucraron el descubrimiento de la W y bosones de calibre Z en colisiones protón-antiprotón en el Super Proton Synchrotron convertido. En 1999, Gerardus 't Hooft y Martinus Veltman recibieron el premio Nobel por demostrar que la teoría electrodébil es renormalizable.

Historia

Después de que el experimento de Wu en 1956 descubriera la violación de la paridad en la interacción débil, comenzó la búsqueda de una forma de relacionar las interacciones débil y electromagnética. Ampliando el trabajo de su asesor de doctorado Julian Schwinger, Sheldon Glashow primero experimentó con la introducción de dos simetrías diferentes, una quiral y otra aquiral, y las combinó de manera que su simetría general no se rompiera. Esto no produjo una teoría renormalizable, y su simetría de calibre tuvo que romperse a mano ya que no se conocía ningún mecanismo espontáneo, pero predijo una nueva partícula, el bosón Z. Esto recibió poca atención, ya que no coincidía con ningún hallazgo experimental.

En 1964, Salam y Ward tuvieron la misma idea, pero predijeron un fotón sin masa y tres bosones de calibre masivos con una simetría rota manualmente. Más tarde, alrededor de 1967, mientras investigaba la ruptura espontánea de la simetría, Weinberg encontró un conjunto de simetrías que predecían un bosón de calibre neutral sin masa. Inicialmente rechazó tal partícula como inútil, luego se dio cuenta de que sus simetrías producían la fuerza electrodébil, y procedió a predecir masas aproximadas para los bosones W y Z. Significativamente, sugirió que esta nueva teoría era renormalizable. En 1971, Gerard 't Hooft demostró que las simetrías de calibre rotas espontáneamente se pueden volver a normalizar incluso con bosones de calibre masivos.

Formulación

El débil ángulo de mezcla de Weinberg

Silencio

_W, y relación entre constantes de acoplamiento

g, g

, y

e

. Adaptado de Lee (1981).

El patrón de isospin débil,

T

₃, y la hipercarga débil,

Y

_W, de las partículas elementales conocidas, mostrando la carga eléctrica,

Q

, a lo largo del ángulo de mezcla débil. El campo Higgs neutral (circulado) rompe la simetría de electroweak e interactúa con otras partículas para darles masa. Tres componentes del campo Higgs se convierten en parte de la masa
W
y
Z
Bosons.

Matemáticamente, el electromagnetismo se unifica con las interacciones débiles como un campo de Yang-Mills con un grupo de calibre SU(2) × U(1), que describe las operaciones formales que se pueden aplicar a los campos de calibre electrodébil sin cambiar la dinámica. del sistema. Estos campos son los campos isospin débiles $W$ ₁, $W$ ₂ y $W$ ₃, y el campo de hipercarga débil $B$ . Esta invariancia se conoce como simetría electrodébil.

Los generadores de SU(2) y U(1) reciben el nombre de isospin débil (etiquetado como $T$ ) y débil hipercarga (etiquetados como $Y$ ) respectivamente. Estos luego dan lugar a los bosones de calibre que median las interacciones electrodébiles: los tres $W$ bosones de isospín débil ( $W$ ₁, $W$ ₂ y $W$ ₃), y el bosón $B$ de hipercarga débil, respectivamente, todos los cuales son "inicialmente" sin masa Estos no son campos físicos todavía, antes de la ruptura espontánea de la simetría y el mecanismo de Higgs asociado.

En el modelo estándar, los bosones W± y Z0, y el fotón, se producen a través de la ruptura de simetría espontánea de la simetría electrodébil SU(2) × U(1)_Y a U(1)_em, efectuado por el mecanismo de Higgs (ver también bosón de Higgs), un elaborado fenómeno teórico del campo cuántico que "espontáneamente" altera la realización de la simetría y reorganiza los grados de libertad.

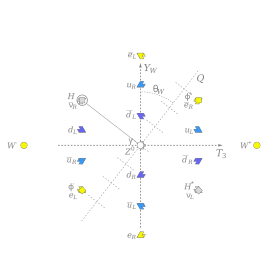
La carga eléctrica surge como la combinación lineal particular (notrivial) de $Y$ _W (hipercarga débil) y el $T$ ₃ componente de isospina débil ${displaystyle ~left(,Q=T_{3}+{tfrac {1}{2}},Y_{mathrm {W} },right)~}$ que hace no pareja al bosón Higgs. Es decir: Los Higgs y el campo electromagnético no tienen ningún efecto en el nivel de las fuerzas fundamentales ("nivel del árbol"), mientras que cualquier otros combinación de la hipercarga y la débil isospin debe interactuar con los Higgs. Esto causa una separación aparente entre la fuerza débil, que interactúa con los Higgs, y el electromagnetismo, que no lo hace. Matemáticamente, la carga eléctrica es una combinación específica de la hipercarga y $T$ ₃ descrito en la figura.

$U(1)$ _em (el grupo de simetría del electromagnetismo únicamente) se define como el grupo generado por esta combinación lineal especial, y el la simetría descrita por el grupo $U(1)$ _em no se rompe, ya que no interactúa directamente con el bosón de Higgs.

La ruptura de simetría espontánea anterior hace que la $W$ ₃ y $B$ se fusionan en dos bosones físicos diferentes con masas diferentes: el
Z⁰
bosón y el fotón ( $γ$ ),

{displaystyle {begin{pmatrix}gamma \Z^{0}end{pmatrix}}={begin{pmatrix}cos theta _{text{W}}&sin theta _{text{W}}\-sin theta _{text{W}}&cos theta _{text{W}}end{pmatrix}}{begin{pmatrix}B\W_{3}end{pmatrix}},}

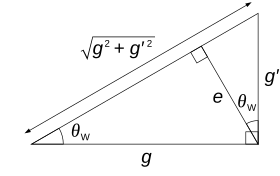
donde $θ$ _W es el ángulo de mezcla débil. Los ejes que representan las partículas esencialmente se acaban de rotar, en ( $W$ ₃, $B$ ) plano, por el ángulo $θ$ _W. Esto también introduce una falta de coincidencia entre la masa de la
Z⁰
y la masa del
W^±
partículas (indicadas como $m$ _Z y $m$ _W, respectivamente),

{displaystyle m_{text{Z}}={frac {m_{text{W}}}{,cos theta _{text{W}},}}~.}

La $W$ ₁ y $W$ ₂ bosones, a su vez, se combinan para producir bosones masivos cargados
W^±
:

{displaystyle W^{pm }={frac {1}{sqrt {2,}}},{bigl (},W_{1}mp iW_{2},{bigr)}~.}

Lagrangiano

Antes de la ruptura de la simetría electrodébil

El Lagrangiano para las interacciones electrodébiles se divide en cuatro partes antes de que se manifieste la ruptura de la simetría electrodébil,

{displaystyle {mathcal {L}}_{text{EW}}={mathcal {L}}_{g}+{mathcal {L}}_{f}+{mathcal {L}}_{h}+{mathcal {L}}_{y}~.}

El $mathcal{L}_g$ término describe la interacción entre los tres $W$ vectores bosons y los $B$ vector boson,

{displaystyle {mathcal {L}}_{g}=-{tfrac {1}{4}}W_{a}^{mu nu }W_{mu nu }^{a}-{tfrac {1}{4}}B^{mu nu }B_{mu nu }}

Donde $W^{amunu}$ () $a=1,2,3$ ) y $B^{munu}$ son los tensores de fuerza de campo para el isospin débil y los campos de control de hipercarga débil.

$mathcal{L}_f$ es el término cinético para los fermions modelo estándar. La interacción de los bosones de calibre y los fermions son a través del derivado covariante de calibre,

{displaystyle {mathcal {L}}_{f}={overline {Q}}_{j}iD!!!!/;Q_{j}+{overline {u}}_{j}iD!!!!/;u_{j}+{overline {d}}_{j}iD!!!!/;d_{j}+{overline {L}}_{j}iD!!!!/;L_{j}+{overline {e}}_{j}iD!!!!/;e_{j}}

donde el subscript $j$ sumas a lo largo de las tres generaciones de helechos; $Q$ , $u$ , y $d$ son el doblet zurdo, el singlet de mano derecha arriba, y el singlet de mano derecha hacia abajo campos de quark; y $L$ y $e$ son los campos de electrones de doble y de mano derecha. El golpe de Feynman ${displaystyle D!!!!/}$ significa la contracción del 4-gradiente con las matrices Dirac, definida como

{displaystyle D!!!!/equiv gamma ^{mu }D_{mu }}

y la derivada covariante (excluyendo el campo de calibre de gluones para la interacción fuerte) se define como

{displaystyle D_{mu }equiv partial _{mu }-i{frac {g'}{2}}Y,B_{mu }-i{frac {g}{2}}T_{j},W_{mu }^{j}}

Aquí. $Y$ es la hipercarga débil y el $T_{j}$ son los componentes del isospin débil.

El ${displaystyle {mathcal {L}}_{h}}$ término describe el campo Higgs $h$ y sus interacciones con sí mismo y los bosones de calibre,

mathcal{L}_h = |D_mu h|^2 - lambda left(|h|^2 - frac{v^2}{2}right)^2

Donde $v$ es el valor de expectativa de vacío.

El ${displaystyle {mathcal {L}}_{y}}$ término describe la interacción Yukawa con los fermions,

{displaystyle {mathcal {L}}_{y}=-y_{u,ij}epsilon ^{ab},h_{b}^{dagger },{overline {Q}}_{ia}u_{j}^{c}-y_{d,ij},h,{overline {Q}}_{i}d_{j}^{c}-y_{e,ij},h,{overline {L}}_{i}e_{j}^{c}+h.c.~,}

y genera sus masas, se manifiestan cuando el campo Higgs adquiere un valor de expectativa de vacío no cero, discutido después. El ${displaystyle y_{u,d,e}^{ij}}$ son matrices de acoplamientos Yukawa.

Después de la ruptura de simetría electrodébil

El lagrangiano se reorganiza a sí mismo a medida que el bosón de Higgs adquiere un valor esperado de vacío que no se desvanece dictado por el potencial de la sección anterior. Como resultado de esta reescritura, se manifiesta la ruptura de la simetría. En la historia del universo, se cree que esto ocurrió poco después del big bang caliente, cuando el universo estaba a una temperatura de 159,5 ± 1,5 GeV (asumiendo el modelo estándar de física de partículas).

Debido a su complejidad, este Lagrangiano se describe mejor dividiéndolo en varias partes de la siguiente manera.

{displaystyle {mathcal {L}}_{text{EW}}={mathcal {L}}_{text{K}}+{mathcal {L}}_{text{N}}+{mathcal {L}}_{text{C}}+{mathcal {L}}_{text{H}}+{mathcal {L}}_{text{HV}}+{mathcal {L}}_{text{WWV}}+{mathcal {L}}_{text{WWVV}}+{mathcal {L}}_{text{Y}}.}

El término cinético $mathcal{L}_K$ contiene todos los términos cuadráticos del lagrangiano, que incluyen los términos dinámicos (los derivados parciales) y los términos de masa (discretamente ausentes del lagrangiano antes de romper la simetría)

{displaystyle {begin{aligned}{mathcal {L}}_{text{K}}=sum _{f}{overline {f}}(ipartial !!!/!;-m_{f})f-{frac {1}{4}}A_{mu nu }A^{mu nu }-{frac {1}{2}}W_{mu nu }^{+}W^{-mu nu }+m_{W}^{2}W_{mu }^{+}W^{-mu }\qquad -{frac {1}{4}}Z_{mu nu }Z^{mu nu }+{frac {1}{2}}m_{Z}^{2}Z_{mu }Z^{mu }+{frac {1}{2}}(partial ^{mu }H)(partial _{mu }H)-{frac {1}{2}}m_{H}^{2}H^{2}~,end{aligned}}}

donde la suma se extiende sobre todos los fermiones de la teoría (quarks y leptons), y los campos ${displaystyle A_{mu nu }}$ , ${displaystyle Z_{mu nu }}$ , $W^-_{munu}$ , y ${displaystyle W_{mu nu }^{+}equiv (W_{mu nu }^{-})^{dagger }}$ se dan como

{displaystyle X_{mu nu }^{a}=partial _{mu }X_{nu }^{a}-partial _{nu }X_{mu }^{a}+gf^{abc}X_{mu }^{b}X_{nu }^{c}~,}

con ' $X$ ' para ser reemplazado por el campo relevante ( $A$ , $Z$ , ${displaystyle W^{pm }}$ ), y $f abc$ por las constantes de la estructura del grupo de calibre adecuado.

La corriente neutral ${displaystyle {mathcal {L}}_{text{N}}}$ y corriente cargada ${displaystyle {mathcal {L}}_{text{C}}}$ componentes del lagrangiano contienen las interacciones entre los fermions y los bosones de calibre,

{displaystyle {mathcal {L}}_{text{N}}=e,J_{mu }^{text{em}},A^{mu }+{frac {g}{,cos theta _{W},}},(,J_{mu }^{3}-sin ^{2}theta _{W},J_{mu }^{text{em}},),Z^{mu }~,}

Donde ${displaystyle ~e=g,sin theta _{text{W}}=g',cos theta _{text{W}}~.}$ La corriente electromagnética ${displaystyle ;J_{mu }^{text{em}};}$ es

{displaystyle J_{mu }^{text{em}}=sum _{f},q_{f},{overline {f}},gamma _{mu },f~,}

Donde $q_f^{}$ son las cargas eléctricas de los fermions. La corriente débil neutral ${displaystyle ;J_{mu }^{3};}$ es

{displaystyle J_{mu }^{3}=sum _{f},I_{f}^{3},{overline {f}},gamma _{mu },{frac {,1-gamma ^{5},}{2}},f~,}

Donde $I_f^3$ es el isospin débil de los fermions.

La parte actual cargada del Lagrangiano viene dada por

{displaystyle {mathcal {L}}_{text{C}}=-{frac {g}{,{sqrt {2,}},}},left[,{overline {u}}_{i},gamma ^{mu },{frac {,1-gamma ^{5},}{2}};M_{ij}^{text{CKM}},d_{j}+{overline {nu }}_{i},gamma ^{mu };{frac {,1-gamma ^{5},}{2}};e_{i},right],W_{mu }^{+}+{text{h.c.}}~,}

Donde ${displaystyle ,nu ,}$ es el campo neutrino de mano derecha, y la matriz CKM ${displaystyle ,M_{ij}^{text{CKM}},}$ determina la mezcla entre la masa y los eigentales débiles de los quarks.

${displaystyle {mathcal {L}}_{text{H}}}$ contiene los términos de interacción de Higgs de tres puntos y cuatro puntos,

{displaystyle {mathcal {L}}_{text{H}}=-{frac {,g,m_{text{H}}^{2},}{,4,m_{text{W}},}};H^{3}-{frac {,g^{2},m_{text{H}}^{2},}{32,m_{text{W}}^{2}}};H^{4}~.}

${displaystyle {mathcal {L}}_{text{HV}}}$ contiene las interacciones de Higgs con gauge vector bosons,

{displaystyle {mathcal {L}}_{text{HV}}=left(,g,m_{text{HV}}+{frac {,g^{2},}{4}};H^{2},right)left(,W_{mu }^{+},W^{-mu }+{frac {1}{,2,cos ^{2},theta _{text{W}},}};Z_{mu },Z^{mu },right)~.}

${displaystyle {mathcal {L}}_{text{WWV}}}$ contiene el medidor de tres puntos autointeracciones,

{displaystyle {mathcal {L}}_{text{WWV}}=-i,g,left[;left(,W_{mu nu }^{+},W^{-mu }-W^{+mu },W_{mu nu }^{-},right)left(,A^{nu },sin theta _{text{W}}-Z^{nu },cos theta _{text{W}},right)+W_{nu }^{-},W_{mu }^{+},left(,A^{mu nu },sin theta _{text{W}}-Z^{mu nu },cos theta _{text{W}},right);right]~.}

${displaystyle ,{mathcal {L}}_{text{WWVV}},}$ contiene el medidor de cuatro puntos autointeracciones,

{displaystyle {begin{aligned}{mathcal {L}}_{text{WWVV}}=-{frac {,g^{2},}{4}},{Biggl {},&{Bigl [},2,W_{mu }^{+},W^{-mu }+(,A_{mu },sin theta _{text{W}}-Z_{mu },cos theta _{text{W}},)^{2},{Bigr ]}^{2}\&-{Bigl [},W_{mu }^{+},W_{nu }^{-}+W_{nu }^{+},W_{mu }^{-}+left(,A_{mu },sin theta _{text{W}}-Z_{mu },cos theta _{text{W}},right)left(,A_{nu },sin theta _{text{W}}-Z_{nu },cos theta _{text{W}},right),{Bigr ]}^{2},{Biggr }}~.end{aligned}}}

${displaystyle ,{mathcal {L}}_{text{Y}},}$ contiene las interacciones Yukawa entre los fermions y el campo Higgs,

{displaystyle {mathcal {L}}_{text{Y}}=-sum _{f},{frac {,g,m_{f},}{2,m_{text{W}}}};{overline {f}},f,H~.}

Contenido relacionado

Más resultados...