Integral trigonométrica

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

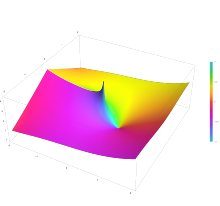
Parcela de la función integral de seno hiperbólico Shi(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplejoPlot3D

Función especial definida por una

Six) (azul) y Ci(xTrazado en la misma parcela.

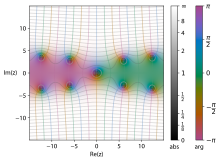
Seno integral en el plano complejo, trazado con una variante de coloración de dominio.

Cosina integral en el plano complejo. Note la rama cortada a lo largo del eje real negativo.

En matemáticas, las integrales trigonométricas son una familia de integrales que involucran funciones trigonométricas.

Integral de seno

Parcela de Six) para

0 \leq x \leq 8 π

Parcela de la función integral cosina Ci(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

Las diferentes definiciones de integrales de seno son

{displaystyle operatorname {Si} (x)=int _{0}^{x}{frac {sin t}{t}},dt}

{displaystyle operatorname {si} (x)=-int _{x}^{infty }{frac {sin t}{t}},dt~.}

Note que el componented ${displaystyle {frac {sin(t)}{t}}}$ es la función sinc, y también la función de Bessel esférica cero. Desde $sinc$ es una función incluso completa (holomorfa sobre todo el plano complejo), $Si$ es entera, extraña, y la integral en su definición se puede tomar a lo largo de cualquier camino que conecta los puntos finales.

Por definición, $Si(x)$ es la antiderivada de $sin x / x$ cuyo valor es cero en $x = 0$ , y $si(x)$ es la antiderivada cuyo valor es cero en $x = \infty$ . Su diferencia viene dada por la integral de Dirichlet,

{displaystyle operatorname {Si} (x)-operatorname {si} (x)=int _{0}^{infty }{frac {sin t}{t}},dt={frac {pi }{2}}quad {text{ or }}quad operatorname {Si} (x)={frac {pi }{2}}+operatorname {si} (x)~.}

En el procesamiento de la señal, las oscilaciones de la integral del seno provocan sobreimpulsos y artefactos de timbre cuando se usa el filtro sinc, y un timbre en el dominio de la frecuencia si se usa un filtro sinc truncado como filtro de paso bajo.

El fenómeno de Gibbs está relacionado: si la integral del seno se considera como la convolución de la función sinc con la función escalón del lado pesado, esto corresponde a truncar la serie de Fourier, que es la causa del fenómeno de Gibbs.

Coseno integral

Parcela de

Ci(x)

para 0

x

≤ 8

π

Las diferentes definiciones de integrales de coseno son

{displaystyle operatorname {Cin} (x)=int _{0}^{x}{frac {1-cos t}{t}},dt~,}

<math alttext="{displaystyle operatorname {Ci} (x)=-int _{x}^{infty }{frac {cos t}{t}},dt=gamma +ln x-int _{0}^{x}{frac {1-cos t}{t}},dtqquad ~{text{ for }}~left|operatorname {Arg} (x)right|Ci⁡ ⁡ ()x)=− − ∫ ∫ xJUEGO JUEGO #⁡ ⁡ ttdt=γ γ +In⁡ ⁡ x− − ∫ ∫ 0x1− − #⁡ ⁡ ttdtparaSilencioArg⁡ ⁡ ()x)Silencio.π π ,{displaystyle operatorname {Ci} (x)=-int _{x}{infty }{frac {cos ♪♪ +ln x-int ¿Qué? {1-cos ############ {text{ for }~left durableoperatorname {Arg} (x)right sobrevivienda:pi ~}<img alt="{displaystyle operatorname {Ci} (x)=-int _{x}^{infty }{frac {cos t}{t}},dt=gamma +ln x-int _{0}^{x}{frac {1-cos t}{t}},dtqquad ~{text{ for }}~left|operatorname {Arg} (x)right|

γ Entendido 0,5721566...

ci

Ci

$Ci(x)$ es el antiderivativo de $# x / x$ (que desaparece como $xto infty$ ). Las dos definiciones están relacionadas por

{displaystyle operatorname {Ci} (x)=gamma +ln x-operatorname {Cin} (x)~.}

$Cin$ es una función uniforme y completa. Por esa razón, algunos textos tratan $Cin$ como la función principal y derivan $Ci$ en términos de $Cin$ .

Integral de seno hiperbólico

La integral del seno hiperbólico se define como

{displaystyle operatorname {Shi} (x)=int _{0}^{x}{frac {sinh(t)}{t}},dt.}

Está relacionado con la integral ordinaria del seno por

{displaystyle operatorname {Si} (ix)=ioperatorname {Shi} (x).}

Integral coseno hiperbólico

La integral del coseno hiperbólico es

Parcela de la función integral de cosina hiperbólica Chi(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplejoPlot3D

<math alttext="{displaystyle operatorname {Chi} (x)=gamma +ln x+int _{0}^{x}{frac {cosh t-1}{t}},dtqquad ~{text{ for }}~left|operatorname {Arg} (x)right|Chi⁡ ⁡ ()x)=γ γ +In⁡ ⁡ x+∫ ∫ 0xcosh⁡ ⁡ t− − 1tdtparaSilencioArg⁡ ⁡ ()x)Silencio.π π ,{displaystyle operatorname {Chi} (x)=gamma +ln x+int _{0}^{x}{frac {cosh t-1}{t}},dtqquad ~{text{ for }~left hypertorname {Arg} (x)derecha se impusopi ~}<img alt="{displaystyle operatorname {Chi} (x)=gamma +ln x+int _{0}^{x}{frac {cosh t-1}{t}},dtqquad ~{text{ for }}~left|operatorname {Arg} (x)right|

gamma

Tiene la expansión de la serie

{displaystyle operatorname {Chi} (x)=gamma +ln(x)+{frac {x^{2}}{4}}+{frac {x^{4}}{96}}+{frac {x^{6}}{4320}}+{frac {x^{8}}{322560}}+{frac {x^{10}}{36288000}}+O(x^{12}).}

Funciones auxiliares

Las integrales trigonométricas se pueden entender en términos de las llamadas "funciones auxiliares"

{displaystyle {begin{array}{rcl}f(x)&equiv &int _{0}^{infty }{frac {sin(t)}{t+x}},dt&=&int _{0}^{infty }{frac {e^{-xt}}{t^{2}+1}},dt&=&operatorname {Ci} (x)sin(x)+left[{frac {pi }{2}}-operatorname {Si} (x)right]cos(x)~,\g(x)&equiv &int _{0}^{infty }{frac {cos(t)}{t+x}},dt&=&int _{0}^{infty }{frac {te^{-xt}}{t^{2}+1}},dt&=&-operatorname {Ci} (x)cos(x)+left[{frac {pi }{2}}-operatorname {Si} (x)right]sin(x)~.end{array}}}

{displaystyle {begin{array}{rcl}{frac {pi }{2}}-operatorname {Si} (x)=-operatorname {si} (x)&=&f(x)cos(x)+g(x)sin(x)~,qquad {text{ and }}\operatorname {Ci} (x)&=&f(x)sin(x)-g(x)cos(x)~.\end{array}}}

Espiral de Nielsen

La espiral de Nielsen.

La espiral formada por el gráfico paramétrico de $si ci$ se conoce como espiral de Nielsen.

{displaystyle x(t)=atimes operatorname {ci} (t)}

{displaystyle y(t)=atimes operatorname {si} (t)}

La espiral está estrechamente relacionada con las integrales de Fresnel y la espiral de Euler. La espiral de Nielsen tiene aplicaciones en el procesamiento de visión, la construcción de carreteras y vías y otras áreas.

Expansión

Se pueden usar varias expansiones para la evaluación de integrales trigonométricas, según el rango del argumento.

Series asintóticas (para grandes argumentos)

{displaystyle operatorname {Si} (x)sim {frac {pi }{2}}-{frac {cos x}{x}}left(1-{frac {2!}{x^{2}}}+{frac {4!}{x^{4}}}-{frac {6!}{x^{6}}}cdots right)-{frac {sin x}{x}}left({frac {1}{x}}-{frac {3!}{x^{3}}}+{frac {5!}{x^{5}}}-{frac {7!}{x^{7}}}cdots right)}

{displaystyle operatorname {Ci} (x)sim {frac {sin x}{x}}left(1-{frac {2!}{x^{2}}}+{frac {4!}{x^{4}}}-{frac {6!}{x^{6}}}cdots right)-{frac {cos x}{x}}left({frac {1}{x}}-{frac {3!}{x^{3}}}+{frac {5!}{x^{5}}}-{frac {7!}{x^{7}}}cdots right)~.}

Estas series son asintóticas y divergentes, aunque se pueden usar para estimaciones e incluso evaluaciones precisas en $ℜ(x) ≫ 1$ .

Serie convergente

{displaystyle operatorname {Si} (x)=sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{frac {x^{3}}{3!cdot 3}}+{frac {x^{5}}{5!cdot 5}}-{frac {x^{7}}{7!cdot 7}}pm cdots }

{displaystyle operatorname {Ci} (x)=gamma +ln x+sum _{n=1}^{infty }{frac {(-1)^{n}x^{2n}}{2n(2n)!}}=gamma +ln x-{frac {x^{2}}{2!cdot 2}}+{frac {x^{4}}{4!cdot 4}}mp cdots }

Estas series son convergentes en cualquier $x$ compleja, aunque para $| x | ≫ 1$ , la serie convergerá lentamente inicialmente, requiriendo muchos términos para una alta precisión.

Derivación de expansión en serie

De la expansión de la serie de Maclaurin del seno:

{displaystyle sin ,x=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+{frac {x^{9}}{9!}}-{frac {x^{11}}{11!}}+cdots }

{displaystyle {frac {sin ,x}{x}}=1-{frac {x^{2}}{3!}}+{frac {x^{4}}{5!}}-{frac {x^{6}}{7!}}+{frac {x^{8}}{9!}}-{frac {x^{10}}{11!}}+cdots }

{displaystyle therefore int {frac {sin ,x}{x}}dx=x-{frac {x^{3}}{3!cdot 3}}+{frac {x^{5}}{5!cdot 5}}-{frac {x^{7}}{7!cdot 7}}+{frac {x^{9}}{9!cdot 9}}-{frac {x^{11}}{11!cdot 11}}+cdots }

Relación con la integral exponencial de argumento imaginario

La función

{displaystyle operatorname {E} _{1}(z)=int _{1}^{infty }{frac {exp(-zt)}{t}},dtqquad ~{text{ for }}~Re (z)geq 0}

Si

Ci

0~.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">E1⁡ ⁡ ()ix)=i()− − π π 2+Si⁡ ⁡ ()x))− − Ci⁡ ⁡ ()x)=iSi⁡ ⁡ ()x)− − ci⁡ ⁡ ()x)parax■0.{displaystyle operatorname [E] _{1}(ix)=ileft(-{frac {pi) }{2}+operatorname {Si} (x)right)-operatorname {Ci} (x)=ioperatorname {si} (x)-operatorname {ci} x)qquad ~{text{ for }~x título0~0~.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/60b4ee5e0d44d4eddc6cdd35c35eda6516601b7a" style="vertical-align: -1.838ex; width:67.062ex; height:4.843ex;"/>

Como cada función respectiva es analítica excepto por el corte en valores negativos del argumento, el área de validez de la relación debe extenderse a (fuera de este rango, términos adicionales que son factores enteros de $π$ aparecen en la expresión).

Los casos de argumento imaginario de la función integro-exponencial generalizada son

{displaystyle int _{1}^{infty }cos(ax){frac {ln x}{x}},dx=-{frac {pi ^{2}}{24}}+gamma left({frac {gamma }{2}}+ln aright)+{frac {ln ^{2}a}{2}}+sum _{ngeq 1}{frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,}

{displaystyle int _{1}^{infty }e^{iax}{frac {ln x}{x}},dx=-{frac {pi ^{2}}{24}}+gamma left({frac {gamma }{2}}+ln aright)+{frac {ln ^{2}a}{2}}-{frac {pi }{2}}ileft(gamma +ln aright)+sum _{ngeq 1}{frac {(ia)^{n}}{n!n^{2}}}~.}

Del mismo modo

{displaystyle int _{1}^{infty }e^{iax}{frac {ln x}{x^{2}}},dx=1+ialeft[-{frac {pi ^{2}}{24}}+gamma left({frac {gamma }{2}}+ln a-1right)+{frac {ln ^{2}a}{2}}-ln a+1right]+{frac {pi a}{2}}{Bigl (}gamma +ln a-1{Bigr)}+sum _{ngeq 1}{frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.}

Evaluación eficiente

Las aproximaciones de Padé de la serie de Taylor convergente proporcionan una manera eficiente de evaluar las funciones para argumentos pequeños. Las siguientes fórmulas, dadas por Rowe et al. (2015), tienen una precisión superior a $10 -16$ para $0 \leq x \leq 4$ ,

{displaystyle {begin{array}{rcl}operatorname {Si} (x)&approx &xcdot left({frac {begin{array}{l}1-4.54393409816329991cdot 10^{-2}cdot x^{2}+1.15457225751016682cdot 10^{-3}cdot x^{4}-1.41018536821330254cdot 10^{-5}cdot x^{6}\~~~+9.43280809438713025cdot 10^{-8}cdot x^{8}-3.53201978997168357cdot 10^{-10}cdot x^{10}+7.08240282274875911cdot 10^{-13}cdot x^{12}\~~~-6.05338212010422477cdot 10^{-16}cdot x^{14}end{array}}{begin{array}{l}1+1.01162145739225565cdot 10^{-2}cdot x^{2}+4.99175116169755106cdot 10^{-5}cdot x^{4}+1.55654986308745614cdot 10^{-7}cdot x^{6}\~~~+3.28067571055789734cdot 10^{-10}cdot x^{8}+4.5049097575386581cdot 10^{-13}cdot x^{10}+3.21107051193712168cdot 10^{-16}cdot x^{12}end{array}}}right)\&~&\operatorname {Ci} (x)&approx &gamma +ln(x)+\&&x^{2}cdot left({frac {begin{array}{l}-0.25+7.51851524438898291cdot 10^{-3}cdot x^{2}-1.27528342240267686cdot 10^{-4}cdot x^{4}+1.05297363846239184cdot 10^{-6}cdot x^{6}\~~~-4.68889508144848019cdot 10^{-9}cdot x^{8}+1.06480802891189243cdot 10^{-11}cdot x^{10}-9.93728488857585407cdot 10^{-15}cdot x^{12}\end{array}}{begin{array}{l}1+1.1592605689110735cdot 10^{-2}cdot x^{2}+6.72126800814254432cdot 10^{-5}cdot x^{4}+2.55533277086129636cdot 10^{-7}cdot x^{6}\~~~+6.97071295760958946cdot 10^{-10}cdot x^{8}+1.38536352772778619cdot 10^{-12}cdot x^{10}+1.89106054713059759cdot 10^{-15}cdot x^{12}\~~~+1.39759616731376855cdot 10^{-18}cdot x^{14}\end{array}}}right)end{array}}}

Las integrales pueden ser evaluadas indirectamente a través de funciones auxiliares $f(x)$ y $g(x)$ , que se definen por

${displaystyle operatorname {Si} (x)={frac {pi }{2}}-f(x)cos(x)-g(x)sin(x)}$		${displaystyle operatorname {Ci} (x)=f(x)sin(x)-g(x)cos(x)}$
o equivalente
${displaystyle f(x)equiv left[{frac {pi }{2}}-operatorname {Si} (x)right]cos(x)+operatorname {Ci} (x)sin(x)}$		${displaystyle g(x)equiv left[{frac {pi }{2}}-operatorname {Si} (x)right]sin(x)-operatorname {Ci} (x)cos(x)}$

Para $xgeq 4$ las funciones racionales de Padé dadas a continuación $f(x)$ y $g(x)$ con error menos de 10⁻¹⁶:

{displaystyle {begin{array}{rcl}f(x)&approx &{dfrac {1}{x}}cdot left({frac {begin{array}{l}1+7.44437068161936700618cdot 10^{2}cdot x^{-2}+1.96396372895146869801cdot 10^{5}cdot x^{-4}+2.37750310125431834034cdot 10^{7}cdot x^{-6}\~~~+1.43073403821274636888cdot 10^{9}cdot x^{-8}+4.33736238870432522765cdot 10^{10}cdot x^{-10}+6.40533830574022022911cdot 10^{11}cdot x^{-12}\~~~+4.20968180571076940208cdot 10^{12}cdot x^{-14}+1.00795182980368574617cdot 10^{13}cdot x^{-16}+4.94816688199951963482cdot 10^{12}cdot x^{-18}\~~~-4.94701168645415959931cdot 10^{11}cdot x^{-20}end{array}}{begin{array}{l}1+7.46437068161927678031cdot 10^{2}cdot x^{-2}+1.97865247031583951450cdot 10^{5}cdot x^{-4}+2.41535670165126845144cdot 10^{7}cdot x^{-6}\~~~+1.47478952192985464958cdot 10^{9}cdot x^{-8}+4.58595115847765779830cdot 10^{10}cdot x^{-10}+7.08501308149515401563cdot 10^{11}cdot x^{-12}\~~~+5.06084464593475076774cdot 10^{12}cdot x^{-14}+1.43468549171581016479cdot 10^{13}cdot x^{-16}+1.11535493509914254097cdot 10^{13}cdot x^{-18}end{array}}}right)\&&\g(x)&approx &{dfrac {1}{x^{2}}}cdot left({frac {begin{array}{l}1+8.1359520115168615cdot 10^{2}cdot x^{-2}+2.35239181626478200cdot 10^{5}cdot x^{-4}+3.12557570795778731cdot 10^{7}cdot x^{-6}\~~~+2.06297595146763354cdot 10^{9}cdot x^{-8}+6.83052205423625007cdot 10^{10}cdot x^{-10}+1.09049528450362786cdot 10^{12}cdot x^{-12}\~~~+7.57664583257834349cdot 10^{12}cdot x^{-14}+1.81004487464664575cdot 10^{13}cdot x^{-16}+6.43291613143049485cdot 10^{12}cdot x^{-18}\~~~-1.36517137670871689cdot 10^{12}cdot x^{-20}end{array}}{begin{array}{l}1+8.19595201151451564cdot 10^{2}cdot x^{-2}+2.40036752835578777cdot 10^{5}cdot x^{-4}+3.26026661647090822cdot 10^{7}cdot x^{-6}\~~~+2.23355543278099360cdot 10^{9}cdot x^{-8}+7.87465017341829930cdot 10^{10}cdot x^{-10}+1.39866710696414565cdot 10^{12}cdot x^{-12}\~~~+1.17164723371736605cdot 10^{13}cdot x^{-14}+4.01839087307656620cdot 10^{13}cdot x^{-16}+3.99653257887490811cdot 10^{13}cdot x^{-18}end{array}}}right)\end{array}}}

Contenido relacionado

Más resultados...