Integral elíptica

En cálculo integral, una integral elíptica es una de varias funciones relacionadas definidas como el valor de ciertas integrales, que fueron estudiadas por primera vez por Giulio Fagnano y Leonhard Euler (c. 1750). Su nombre proviene de su origen original en relación con el problema de encontrar la longitud del arco de una elipse.

Las matemáticas modernas definen una "integral elíptica" como cualquier función f que se puede expresar en la forma

f()x)=∫ ∫ cxR()t,P()t))dt,{displaystyle f(x)=int _{c}{x}Rleft(t,{sqrt {P(t)}right),dt,}

donde R es una función racional de sus dos argumentos, P es un polinomio de grado 3 o 4 sin raíces repetidas, y c es una constante.

En general, las integrales en esta forma no se pueden expresar en términos de funciones elementales. Las excepciones a esta regla general son cuando P tiene raíces repetidas, o cuando R(x, y) no contiene potencias impares de y o si el integral es pseudo-elíptica. Sin embargo, con la fórmula de reducción apropiada, cada integral elíptica puede convertirse en una forma que involucre integrales sobre funciones racionales y las tres formas canónicas de Legendre (es decir, las integrales elípticas de primera, segunda y tercera clase).

Además de la forma de Legendre que se muestra a continuación, las integrales elípticas también se pueden expresar en la forma simétrica de Carlson. Se puede obtener información adicional sobre la teoría de la integral elíptica mediante el estudio del mapeo de Schwarz-Christoffel. Históricamente, las funciones elípticas se descubrieron como funciones inversas de integrales elípticas.

Notación de argumento

Las integrales elípticas incompletas son funciones de dos argumentos; integrales elípticas completas son funciones de un solo argumento. Estos argumentos se expresan en una variedad de formas diferentes pero equivalentes (dan la misma integral elíptica). La mayoría de los textos se adhieren a un esquema de nomenclatura canónico, utilizando las siguientes convenciones de nomenclatura.

Para expresar un argumento:

• α, el ángulo modular
• k = pecado α, el modulo elíptico o excentricidad
• m = k² = pecado² α, el parámetro

Cada una de las tres cantidades anteriores está completamente determinada por cualquiera de las otras (dado que no son negativas). Por lo tanto, se pueden usar indistintamente.

El otro argumento también se puede expresar como φ, la amplitud, o como x o u, donde x = sin φ = sn u y sn es una de las funciones elípticas jacobianas.

Especificar el valor de cualquiera de estas cantidades determina las demás. Tenga en cuenta que u también depende de m. Algunas relaciones adicionales que involucran u incluyen

#⁡ ⁡ φ φ =cn⁡ ⁡ u,y1− − mpecado2⁡ ⁡ φ φ =♪⁡ ⁡ u.{displaystyle cos varphi =operatorname {cn} u,quad {textrm {y}quad {sqrt {1-msin ^{2}varphi ¿Qué?

La última a veces se denomina amplitud delta y se escribe como Δ(φ) = dn u . A veces la literatura también se refiere al parámetro complementario, el módulo complementario o el ángulo modular complementario. Estos se definen con más detalle en el artículo sobre períodos trimestrales.

En esta notación, el uso de una barra vertical como delimitador indica que el argumento que le sigue es el "parámetro" (como se define arriba), mientras que la barra invertida indica que es el ángulo modular. El uso de un punto y coma implica que el argumento que lo precede es el seno de la amplitud:

F()φ φ ,pecado⁡ ⁡ α α )=F()φ φ ▪ ▪ pecado2⁡ ⁡ α α )=F()φ φ ∖ ∖ α α )=F()pecado⁡ ⁡ φ φ ;pecado⁡ ⁡ α α ).{displaystyle F(varphisin alpha)=Fleft(varphi mid sin ^{2}alpha right)=F(varphi setminus alpha)=F(sin varphi;sin alpha).}

Todavía hay otras convenciones para la notación de integrales elípticas empleadas en la literatura. La notación con argumentos intercambiados, F(k, φ), se encuentra a menudo; y de manera similar E(k, φ) para la integral del segundo tipo. Abramowitz y Stegun sustituyen la integral del primer tipo, F(φ, k), para el argumento φ en su definición de las integrales de segundo y tercer tipo, a menos que este argumento vaya seguido de una barra vertical: es decir, E(F(φ, k) | k²) para E(φ | k²). Además, sus integrales completas emplean el parámetro k² como argumento en lugar del módulo k, es decir, K(k ²) en lugar de K(k). Y la integral de tercer tipo definida por Gradshteyn y Ryzhik, Π(φ, n, k) , pone la amplitud φ primero y no la "característica" n.

Por lo tanto, se debe tener cuidado con la notación al usar estas funciones, porque varias referencias y paquetes de software respetables usan diferentes convenciones en las definiciones de las funciones elípticas. Por ejemplo, el software Mathematica de Wolfram y Wolfram Alpha definen la integral elíptica completa del primer tipo en términos del parámetro m, en lugar de el módulo elíptico k.

Integral elíptica incompleta de primera clase

La integral elíptica incompleta de primer tipo F se define como

F()φ φ ,k)=F()φ φ ▪ ▪ k2)=F()pecado⁡ ⁡ φ φ ;k)=∫ ∫ 0φ φ dSilencio Silencio 1− − k2pecado2⁡ ⁡ Silencio Silencio .{displaystyle F(varphik)=Fleft(varphi mid k^{2}right)=F(sin varphi;k)=int ¿Qué? ♫{sqrt {1-k^{2}sin ^{2}theta }}}

Esta es la forma trigonométrica de la integral; sustituyendo t = sin θ y x = sin φ, se obtiene la forma normal de Legendre:

F()x;k)=∫ ∫ 0xdt()1− − t2)()1− − k2t2).{displaystyle F(x;k)=int ¿Por qué?

Equivalentemente, en términos de amplitud y ángulo modular se tiene:

F()φ φ ∖ ∖ α α )=F()φ φ ,pecado⁡ ⁡ α α )=∫ ∫ 0φ φ dSilencio Silencio 1− − ()pecado⁡ ⁡ Silencio Silencio pecado⁡ ⁡ α α )2.{displaystyle F(varphi setminus alpha)=F(varphisin alpha)=int _{0}^{varphi }{frac {dtheta }{sqrt {1-left(theta sin alpha right)}}}}}}}

Con x = sn(u, k) se tiene:

F()x;k)=u;{displaystyle F(x;k)=u;}

La integral elíptica incompleta del primer tipo tiene el siguiente teorema de adición:

F[arctan⁡ ⁡ ()x),k]+F[arctan⁡ ⁡ ()Sí.),k]=F[arctan⁡ ⁡ ()xk.2Sí.2+1Sí.2+1)+arctan⁡ ⁡ ()Sí.k.2x2+1x2+1),k]{bigr]}+F{bigl [}arctan(x),k{bigr]}+F{bigl [}arctan(y),k{bigr]}=Fleft[arctanleft({frac {x{sqrt {k'^{2}y^{2}+1}}{sqrt {y^{2}+1}}right)+arctan left({frac {y{sqrt {k'^{2}x^{2}+1} {sqrt {x^{2}+1}right),kright]}

El módulo elíptico se puede transformar de esta manera:

F[arcsin⁡ ⁡ ()x),k]=21+1− − k2F[arcsin⁡ ⁡ ()()1+1− − k2)x1+1− − k2x2),1− − 1− − k21+1− − k2]{displaystyle F{bigl [}arcsin(x),k{bigr]}={frac {2}{1+{sqrt {1-k^{2}}}Fleft[arcsin left({frac {left(1+{sqrt {1-k^{2}}right)x}{1+{sqrt {1-k^{2}x^{2}}}}}derecha),{frac {1-{sqrt {1-k^{2}}{1+{sqrt {1-k^{2}}}} {}}}}}}}} {0}}}}

Integral elíptica incompleta de segunda especie

La integral elíptica incompleta de segundo tipo E en forma trigonométrica es

E()φ φ ,k)=E()φ φ Silenciok2)=E()pecado⁡ ⁡ φ φ ;k)=∫ ∫ 0φ φ 1− − k2pecado2⁡ ⁡ Silencio Silencio dSilencio Silencio .{displaystyle E(varphik)=Eleft(varfi, k^{2}right)=E(sin varphi;k)=int _{0}{varphi }{sqrt {1-k^{2}sin ^{2}theta }dtheta.}

Sustituyendo t = sin θ y x = sin φ, se obtiene la forma normal de Legendre:

E()x;k)=∫ ∫ 0x1− − k2t21− − t2dt.{displaystyle E(x;k)=int ¿Qué? {1-k^{2}t^{2}}{sqrt {1-t^{2}},dt.}

Equivalentemente, en términos de amplitud y ángulo modular:

E()φ φ ∖ ∖ α α )=E()φ φ ,pecado⁡ ⁡ α α )=∫ ∫ 0φ φ 1− − ()pecado⁡ ⁡ Silencio Silencio pecado⁡ ⁡ α α )2dSilencio Silencio .{displaystyle E(varphi setminus alpha)=E(varphisin alpha)=int _{0}^{varphi }{sqrt {1-left(sin thetaalpha right)}}dtheta.}

Las relaciones con las funciones elípticas de Jacobi incluyen

E()sn⁡ ⁡ ()u;k);k)=∫ ∫ 0u♪2⁡ ⁡ ()w;k)dw=u− − k2∫ ∫ 0usn2⁡ ⁡ ()w;k)dw=()1− − k2)u+k2∫ ∫ 0ucn2⁡ ⁡ ()w;k)dw.{displaystyle {begin{aligned}E{bigl (}operatorname {sn} (u;k);k{bigr)} ¿Qué? ¿Por qué? ¿Por qué?

La longitud del arco meridiano desde el ecuador hasta la latitud φ se escribe en términos de E:

m()φ φ )=a()E()φ φ ,e)+d2dφ φ 2E()φ φ ,e)),{displaystyle m(varphi)=aleft(E(varphie)+{frac {d^{2}{dvarphie - Sí.

La integral elíptica incompleta del segundo tipo tiene el siguiente teorema de adición:

E[arctan⁡ ⁡ ()x),k]+E[arctan⁡ ⁡ ()Sí.),k]=E[arctan⁡ ⁡ ()xk.2Sí.2+1Sí.2+1)+arctan⁡ ⁡ ()Sí.k.2x2+1x2+1),k]+k2xSí.k.2x2Sí.2+x2+Sí.2+1()xk.2Sí.2+1Sí.2+1+Sí.k.2x2+1x2+1){bign]}+E{bigl [}arctan(x),k{bigr]}+E{bigl [}arctan(y),k{bigr]}=Eleft[arctanleft({frac {x{sqrt {k'^{2}y^{2}+1}}{sqrt {y^{2}+1}}right)+arctan left({frac {y{sqrt {k'^{2}x^{2}+1}}{sqrt {x^{2}+1}}right),kright]+{frac {k^{2}xy}{2}x^{2}y^{2}+x^{2}+y^{2}+1}}left({frac} {x{sqrt {k'^{2}y^{2}+1}{sqrt {y^{2}+1}}+{frac} {sqrt {k'^{2}x^{2}+1}{sqrt {x^{2}+1}}}right)}

El módulo elíptico se puede transformar de esta manera:

E[arcsin⁡ ⁡ ()x),k]=()1+1− − k2)E[arcsin⁡ ⁡ ()()1+1− − k2)x1+1− − k2x2),1− − 1− − k21+1− − k2]− − 1− − k2F[arcsin⁡ ⁡ ()x),k]+k2x1− − x21+1− − k2x2{displaystyle E{bigl [}arcsin(x),k{bigr]}=left(1+{sqrt) {1-k^{2}}right)Eleft[arcsin left({frac {left(1+{sqrt) {1-k^{2}}right)x}{1+{sqrt {1-k^{2}x^{2}}}}}derecha),{frac {1-{sqrt {1-k^{2}}{1+{sqrt Está bien. {1-k^{2}}F{bigl [}arcsin(x),k{bigr]}+{frac {k^{2}x{sqrt {1-x^{2}}{1+{sqrt {1-k^{2}x^{2}}}}

Integral elíptica incompleta de tercer tipo

La integral elíptica incompleta de tercer tipo Π es

▪ ▪ ()n;φ φ ∖ ∖ α α )=∫ ∫ 0φ φ 11− − npecado2⁡ ⁡ Silencio Silencio dSilencio Silencio 1− − ()pecado⁡ ⁡ Silencio Silencio pecado⁡ ⁡ α α )2{displaystyle Pi (n;varphi setminus alpha)=int _{0}^{varphi }{frac {1}{1-nsin ^{2}theta }{frac {dtheta }{sqrt {1-left(sin theta sin alpha right)^{2}}}}}

o

▪ ▪ ()n;φ φ Silenciom)=∫ ∫ 0pecado⁡ ⁡ φ φ 11− − nt2dt()1− − mt2)()1− − t2).{displaystyle Pi (n;varphi,m)=int _{0}{sin varphi }{frac {1}{1-nt^{2}}}{frac {dt}{sqrt {left(1-mt^{2}right)}}}}}} {}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

El número n se denomina característica y puede tomar cualquier valor, independientemente de los demás argumentos. Sin embargo, tenga en cuenta que el valor Π(1; π/2 | m) es infinito, para cualquier m.

Una relación con las funciones elípticas jacobianas es

▪ ▪ ()n;am⁡ ⁡ ()u;k);k)=∫ ∫ 0udw1− − nsn2⁡ ⁡ ()w;k).{displaystyle Pi {bigl (}n;,operatorname {am} (u;k);,k{bigr)}=int _{0}{u}{u}{frac {dw}{1-n,operatorname {sn} ^{2}(w;k)}}}

La longitud del arco meridiano desde el ecuador hasta la latitud φ también está relacionada con un caso especial de Π:

m()φ φ )=a()1− − e2)▪ ▪ ()e2;φ φ Silencioe2).{displaystyle m(varphi)=aleft(1-e^{2}right)Pi left(e^{2};varphi , sometida,e^{2}right). }

Integral elíptica completa de primera especie

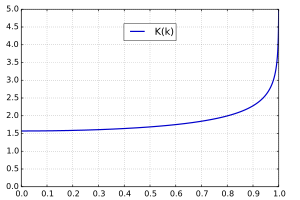
Parcela de la integral elíptica completa del primer tipo K()k)

Se dice que las integrales elípticas son 'completas' cuando la amplitud φ = π/2 y por lo tanto x = 1. La integral elíptica completa de primera clase K puede definirse como

K()k)=∫ ∫ 0π π 2dSilencio Silencio 1− − k2pecado2⁡ ⁡ Silencio Silencio =∫ ∫ 01dt()1− − t2)()1− − k2t2),{displaystyle K(k)=int ¿Qué? {}{2}{frac {dtheta ♫{sqrt {1-k^{2}sin ^{2}theta ♪♪ ¿Por qué? {fnMicrosoft Sans Serif} }

K()k)=F()π π 2,k)=F()π π 2Silenciok2)=F()1;k).{displaystyle K(k)=Fleft({tfrac {pi }{2},kright)=Fleft({tfrac {pi }{2}, la vida,k^{2}right)=F(1;k). }

Se puede expresar como una serie de potencias

K()k)=π π 2.. n=0JUEGO JUEGO ()()2n)!22n()n!)2)2k2n=π π 2.. n=0JUEGO JUEGO ()P2n()0))2k2n,{displaystyle K(k)={frac {pi {2}}sum _{n=0}{infty }left({frac {(2n)}{2n} {2n}(n)} {2n} {2}}right)^{2}k^{2n}={frac {pic {pic {i} {fn0} {fn0}}}}}}}}}f}f}}}f}f}}}f}f}f}f}}f}f}fnf}f}fnfn9}fnfnfnfnfnfnfn9}fnfn9}fnfnfn}}}fnfnfnfn9}fnfnfnfnfn}}fnhnfn}fn}fnfnfnfnhn } {2}sum _{n=0}{infty }{bigl (}P_{2n}(0){bigr)} {2}k^{2n}}

donde P_n son los polinomios de Legendre, que es equivalente a

K()k)=π π 2()1+()12)2k2+()1⋅ ⋅ 32⋅ ⋅ 4)2k4+⋯ ⋯ +()()2n− − 1)!!()2n)!!)2k2n+⋯ ⋯ ),{displaystyle K(k)={frac {pi ¡Bien!

donde n!! denota el factorial doble. En términos de la función hipergeométrica de Gauss, la integral elíptica completa del primer tipo se puede expresar como

K()k)=π π 22F1()12,12;1;k2).{displaystyle K(k)={tfrac {pi }{2},{}_{2} {1}left({tfrac} {1}{2}},{tfrac {1}{2};1;k^{2}right).}

La integral elíptica completa del primer tipo a veces se denomina cuarto de período. Se puede calcular de manera muy eficiente en términos de la media aritmético-geométrica:

K()k)=π π 2agm⁡ ⁡ ()1,1− − k2).{displaystyle K(k)={frac {pi #{2operatorname {agm} left(1,{sqrt {1-k^{2}} {}}}}}}

Por lo tanto, el módulo se puede transformar de esa manera:

K()k)=π π 2agm⁡ ⁡ ()1,1− − k2)=π π 2agm⁡ ⁡ ()12+1− − k22,1− − k24)=π π ()1+1− − k2)agm⁡ ⁡ ()1,21− − k24()1+1− − k2))=21+1− − k2K()1− − 1− − k21+1− − k2){displaystyle {begin{aligned}K(k) ##{2operatorname {agm} left(1,{sqrt {1-k^{2}right)}[4pt] #{2operatorname {agm} left({frac {1}{2}} {sqrt {1-k^{2}}{2}},{sqrt[{4}}{1-k^{2}}}}}}\[4pt] correspond={frac {pi }{left(1+{sqrt}}}}}}}}}}}\[4pt]} {={4pt]}{c}{c}}}}{c}}}}}}}{c}}}}}{c}}}}}}{c}{c}}{c}}}}}}}}}}}}}}{c}}}}}}{c} {c}}}}}}}}}}}}}}}}{c}}}{c}}}}}}}}}}} {c}}}}}}}{c}}}}}}}}}}}} {c}}}}}}} {1-k^{2}}derecha)fnuncio {agm}left(1,{frac {2{sqrt[{4} {1-k^{2}}}}{left(1+{sqrt {1-k^{2}}right)}[4pt] {1-k^{2}}Kleft({frac {1-{sqrt {1-k^{2}}{1+{sqrt {1-k^{2}}} {fnMicrosoft Sans Serif}}

Esta expresión es válida para todos n▪ ▪ N{displaystyle nin mathbb {N} y 0 ≤ k ≤ 1:

K()k)=n[.. a=1n♪⁡ ⁡ ()2anK()k);k)]− − 1K[kn∏ ∏ a=1nsn⁡ ⁡ ()2a− − 1nK()k);k)2]{displaystyle K(k)=nleft[sum ¿Por qué? ¿Por qué? {2a-1}{n}K(k);kright)^{2}right]

Relación con la función gamma

Si k² = λ()i√r) y r▪ ▪ Q+{displaystyle rin mathbb {fnK} (donde) λ es la función modular de lambda), entonces K()k) es expresible en forma cerrada en términos de la función gamma. Por ejemplo, r = 2 y r = 7 dar, respectivamente,

K()2− − 1)=.. ()18).. ()38)2+1824π π ,{displaystyle Kleft({sqrt {2}-1right)={frac {Gammaleft {frac}derecha]Gammaleft({frac {3}{8}}derecha){sqrt {sqrt {2}+1}} {8{4}{2} {sqrt {sqrt {pi}} {sqrt {sqrt} {i}} {sq}}} {sqrt {sqrt {sqrt}} {i}}} {sq}}}}}}} {}}}} {}}}}}} {} {}}}}} {}}}}}} {8{8{8{8{8{8 {sq}} {sq} {sq} {sq} {sq} {sq} {sq}}}}}}} {} {sq} {sq} {} {sq}} {} {sq} {sq}} {sq}}} {}}} {} {} {}}}}} {} {} {} {sq}}}}}}}}}}}}}}}}} {} {}} { ♪♪

y

K()3− − 742)=.. ()17).. ()27).. ()47)474π π .{displaystyle Kleft({frac {3-{sqrt {7}}{4{sqrt {2}}}}right)={frac {Gammaleft({frac {1}{7}right)Gammaleft({frac {2}{7}right)Gammaleft({f}{4}{4}{4}{4}{7}}}{4}}} {sq} {}}}}}}}}}}}}}}{4}}}}}{4}}}}}}}{4}}}}}}}{4}}}}}}} {}}}}}}}}}}}}}}}}}{4}}} {f}}}} {f}}}}{4}}}}{4}}}}} {f}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { }}

Más generalmente, la condición de que

iK.K=iK()1− − k2)K()k){displaystyle {frac {fnK}}={frac} {iKleft({sqrt {1-k^{2}}}} {K(k)}}}

K()e5π π i/6)=e− − π π i/12.. 3()13)34423π π .{displaystyle Kleft(e^{5pi i/6}right)={frac {e^{-pi i/12}Gamma ^{3}left({frac {1}right){sqrt[{4}}}}{4{sqrt[{3}}}{2}pi}}pi}}} {}} {}}}}}}} {i}}}}}}}}}{4}{4}{4}}}}}{4}{4}}}}}}}{4}{4}}}}{4}}}}}}}}}}}}}{4}{4}}} {sq}}}{4}} {sq}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{4}}}}}}{4}}}}}}}}}}}{4}}}}}}}}}} { }}

Relación con la función theta de Jacobi

La relación con la función theta de Jacobi viene dada por

K()k)=π π 2Silencio Silencio 32()q),{displaystyle K(k)={frac {pi } {2}theta _{3} {2}(q),}

q()k)=exp⁡ ⁡ ()− − π π K()1− − k2)K()k)).{displaystyle q(k)=exp left(-pi {frac {Kleft({sqrt {1-k^{2}}derecha)}derecha). }

Expresiones asintóticas

K()k).. π π 2+π π 8k21− − k2− − π π 16k41− − k2{displaystyle Kleft(kright)approx {fnMicroc} - ¿Qué? }{8}{frac {k^{2}{1-k^{2}}-{frac} {pi}{16}{frac} {k^{4}{1-k^{2}}

Ecuación diferencial

La ecuación diferencial para la integral elíptica de primera especie es

ddk()k()1− − k2)dK()k)dk)=kK()k){displaystyle {frac {d}left(kleft(1-k^{2}right){frac} ¿Qué? }

Una segunda solución a esta ecuación es K(√1 − k²). Esta solución satisface la relación

ddkK()k)=E()k)k()1− − k2)− − K()k)k.{displaystyle {frac {d}K(k)={frac {E(k)}{kleft(1-k^{2}right)}}-{frac {K(k)}}}}}} {fnK}} {f}} {fnK}}}}

Fracción continua

Una expansión en fracción continua es:

K()k)2π π =− − 14+.. n=0JUEGO JUEGO qn1+q2n=− − 14+11− − q+()1− − q)21− − q3+q()1− − q2)21− − q5+q2()1− − q3)21− − q7+q3()1− − q4)21− − q9+⋯ ⋯ ,{displaystyle {frac {K(k)}{2pi }=-{frac {1}{4}+sum _{n=0}{infty {q}{n}{1+q^{2n}=-{frac} {1}{4}+{cfrac {1}{1-q+{cfrac {left(1-qright)}{2}{1-q^{3}+{cfrac {qleft(1-q^{2}right)}{1-q^{5}+{cfrac {q^{2}left(1-q^{3}right)}{2}{1-q^{7}+{cfrac {q^{3}left(1-q^{4}right)}{1-q^{9}+cdots }} {}}}}}}}

Integral elíptica completa de segunda especie

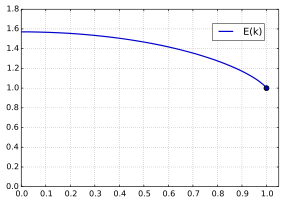
Parcela de la integral elíptica completa del segundo tipo E()k)

La integral elíptica completa de segundo tipo E se define como

E()k)=∫ ∫ 0π π 21− − k2pecado2⁡ ⁡ Silencio Silencio dSilencio Silencio =∫ ∫ 011− − k2t21− − t2dt,{displaystyle E(k)=int ¿Qué? }{2}{sqrt {1-k^{2}Theta},dtheta =int ¿Qué? {1-k^{2}t^{2}}{sqrt {1-t^{2}},dt,}

o más compactamente en términos de la integral incompleta del segundo tipo E(φ,k) como

E()k)=E()π π 2,k)=E()1;k).{displaystyle E(k)=Eleft({tfrac {pi }{2},kright)=E(1;k). }

Para una elipse con semieje mayor a y semieje menor b y excentricidad e = √1 − b²/a², la integral elíptica completa de segundo tipo E(e) es igual a un cuarto de la circunferencia C de la elipse medida en unidades del semieje mayor a. En otras palabras:

C=4aE()e).{displaystyle C=4aE(e). }

La integral elíptica completa de segundo tipo se puede expresar como una serie de potencias

E()k)=π π 2.. n=0JUEGO JUEGO ()()2n)!22n()n!)2)2k2n1− − 2n,{displaystyle E(k)={frac {pi {fnK}sum _{n=0}{infty }left({frac {(2n)}{2n}left(n!right)}right)^{2}{2}{frac}{2n}}{2n}}}{2n=0}}} {fn0}}}}}}}f}{2}}}}}{2}}}}{2}} {f}}}}{2}}}}}}}{2} {f}} {f}} {f}}f}}}}}}}}}}f}}}f}f}}}}}{2}{f}}f}f}f}}}}}f}f}f}f}f}f}}}}}}f}}}}}}}f}f}f}f}f}f}}f}}}}} {k^{2n} {1-2n}}}

que es equivalente a

E()k)=π π 2()1− − ()12)2k21− − ()1⋅ ⋅ 32⋅ ⋅ 4)2k43− − ⋯ ⋯ − − ()()2n− − 1)!!()2n)!!)2k2n2n− − 1− − ⋯ ⋯ ).{displaystyle E(k)={frac {pi {fnK}}left(1-left({frac {1}{2}right)^{2}{frac {k^{2}{1}}left({frac {1cdot 3}{2cdot 4}right)}{2}{2}{frac}{2}{frac {k^{4}{3}}-cdots -left! {k^{2n}{2n-1}-cdots right).}

En términos de la función hipergeométrica de Gauss, la integral elíptica completa de segundo tipo se puede expresar como

E()k)=π π 22F1()12,− − 12;1;k2).{displaystyle E(k)={tfrac {pi }{2},{}_{2} {1}left({tfrac} {1}{2},-{tfrac {1}{2};1;k^{2}right).}

El módulo se puede transformar de esa manera:

E()k)=()1+1− − k2)E()1− − 1− − k21+1− − k2)− − 1− − k2K()k){displaystyle E(k)=left(1+{sqrt Eleft {1-{sqrt {1-k^{2}}{1+{sqrt {1-k^{2}}}}right)-{sqrt {1-k^{2}, K(k)}

Cálculo

Al igual que la integral del primer tipo, la integral elíptica completa del segundo tipo se puede calcular de manera muy eficiente utilizando la media aritmético-geométrica.

Definir secuencias a_n y g_n, donde a₀ = 1, g₀ = √1 − k² = k′ y las relaciones de recurrencia a_{n + 1} = a_n + g_n/2, g_{n + 1} = √a_n g_n espera. Además, definir

cn=Silencioan2− − gn2Silencio.{displaystyle - ¿Qué?

Por definición,

aJUEGO JUEGO =limn→ → JUEGO JUEGO an=limn→ → JUEGO JUEGO gn=agm⁡ ⁡ ()1,1− − k2).{displaystyle a_{infty }=lim _{nto infty }a_{n}=lim _{nto infty }g_{n}=operatorname {agm} left(1,{sqrt {1-k^{2}}derecha).}

También

limn→ → JUEGO JUEGO cn=0.{displaystyle lim _{nto infty }c_{n}=0.}

Entonces

E()k)=π π 2aJUEGO JUEGO ()1− − .. n=0JUEGO JUEGO 2n− − 1cn2).{displaystyle E(k)={frac {pi }{2a_{infty }left(1-sum ¿Qué? ¿Qué?

En la práctica, la media aritmético-geométrica simplemente se calcularía hasta cierto límite. Esta fórmula converge cuadráticamente para todos los |k| ≤ 1. Para acelerar aún más el cálculo, la relación c_{n + 1} = c_n²/4a_{n + 1}.

Además, si k² = λ()i√r) y r▪ ▪ Q+{displaystyle rin mathbb {fnK} (donde) λ es la función modular de lambda), entonces E()k) es expresible en forma cerrada en términos de

K()k)=π π 2agm⁡ ⁡ ()1,1− − k2){displaystyle K(k)={frac {pi #{2operatorname {agm} left(1,{sqrt {1-k^{2}}derecha)}}

E()12)=K()12)+π π 4K()12),{displaystyle Eleft({frac {1}{sqrt {2}}right)=Kleft({frac {1}{sqrt {2}}}}right)+{frac {pic {pi)} } {4Kleft({frac {1}}derecha)} }

E()3− − 742)=7+2714K()3− − 742)+π π 728K()3− − 742).{displaystyle Eleft({frac {3-{sqrt {7}} {4{sqrt {2}}}}derecha)={frac {7+2{sqrt {7}}}{14}}Kleft({fracfrac {3-{sqrt {7}} {4{sqrt {2}}}}right)+{frac {pi}}} {fnK}} {f}}}} {fn9}} {fnfnK}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {justo}}}}}}}}}}}}}}}}}}}} { {cHFF} {7}}{28Kleft({frac} {3-{sqrt {7}} {4{sqrt {2}} {}}}}} {}}} {4{sqrt {sqrt {}}}}} {}}}}}}}} {}}} {}}} {}}} {}}} {}}} {}} {}}}}}}}} {4}}}}} {}}}}}} {}}} {}}}}}} {}}}}} {}}}}}}}}}}}} {} {}}} {}}}}}} {} {}}} {} {}}}}}}}}}}}}}}}}} {} {} {}}}}}}} {} {}}}} {} {}}}}}} {}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Derivada y ecuación diferencial

dE()k)dk=E()k)− − K()k)k{displaystyle {frac {dE(k)}{dk}={frac {E(k)-K(k)} {k}}}}

()k2− − 1)ddk()kdE()k)dk)=kE()k){displaystyle left(k^{2}-1right){frac {d} {dk}left(k;{frac} {dE(k)}{dk}right)=kE(k)}

Una segunda solución a esta ecuación es E(√1 − k²) − K(√1 − k²).

Integral elíptica completa de tercer tipo

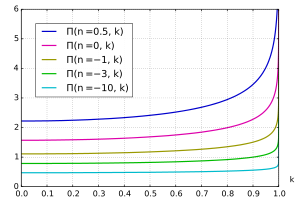
Parcela de la integral elíptica completa del tercer tipo ■n,k) con varios valores fijos n

La integral elíptica completa de tercer tipo Π se puede definir como

▪ ▪ ()n,k)=∫ ∫ 0π π 2dSilencio Silencio ()1− − npecado2⁡ ⁡ Silencio Silencio )1− − k2pecado2⁡ ⁡ Silencio Silencio .{displaystyle Pi (n,k)=int _{0}^{frac {pi {2} {fn} {fnfnsfnsn}theta right){sqrt {1-k^{2}sin ^{2}theta - Sí.

Tenga en cuenta que a veces la integral elíptica de tercer tipo se define con un signo inverso para la característica n,

▪ ▪ .()n,k)=∫ ∫ 0π π 2dSilencio Silencio ()1+npecado2⁡ ⁡ Silencio Silencio )1− − k2pecado2⁡ ⁡ Silencio Silencio .{displaystyle Pi '(n,k)=int ¿Qué? - Sí.

Al igual que las integrales elípticas completas de primer y segundo tipo, la integral elíptica completa de tercer tipo se puede calcular de manera muy eficiente utilizando la media aritmético-geométrica.

Derivadas parciales

∂ ∂ ▪ ▪ ()n,k)∂ ∂ n=12()k2− − n)()n− − 1)()E()k)+1n()k2− − n)K()k)+1n()n2− − k2)▪ ▪ ()n,k))∂ ∂ ▪ ▪ ()n,k)∂ ∂ k=kn− − k2()E()k)k2− − 1+▪ ▪ ()n,k)){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {k} {n-k^{2}}left({frac {E(k)}{k^{2}-1}+ Pi (n,k)right)end{aligned}}

Relaciones funcionales

Relación de Legendre:

K()k)E()1− − k2)+E()k)K()1− − k2)− − K()k)K()1− − k2)=π π 2.{displaystyle K(k)Eleft({sqrt {1-k^{2}}right)+E(k)Kleft({sqrt) {1-k^{2}}right)-K(k)Kleft({sqrt) {1-k^{2}}right)={frac {pi} } {2}}.